基于累积残差贡献率的传感器故障定位方法
安星,刘纲,张亮亮,李立力
(重庆大学 土木工程学院;山地城镇建设与新技术教育部重点实验室,重庆 400045)
结构健康监测旨在通过监测结构行为及时识别结构损伤,实时评估结构性能,已成为土木工程领域的重要研究方向[1]。如今,越来越多的桥梁都安装了结构健康监测系统,其中,传感器是健康监测系统最前端的设备,用于获取结构响应及采集各种监测信息,其精度和性能的好坏将直接影响最终的评估结果[2]。然而,相较于桥梁上百年的使用寿命而言,传感器的使用寿命仅为十几年甚至几年。传感器在使用过程中会因为老化或外界因素影响而出现故障,这会使结构安全状态评估出现漏报或误报,造成不必要的经济损失。
近年来,传感器故障问题已逐步引起业界专家的重视,并开展了初步的理论研究。在传感器故障的统计分类方面,何富君等[3]总结了传感器的4类典型故障:卡死、恒增益、固定偏差和线性偏差。Yi等[4]对其进行了拓展,将传感器的故障类型划分为7类:固定偏差、线性偏差、恒增益、精度下降、卡死、白噪声卡死、零线漂移。在桥梁结构健康监测领域,如何实现传感器故障诊断的研究报道不多,但在控制工程领域,大量学者和工程界人士开展了深入研究,取得了丰硕成果。已有的传感器故障诊断方法可大致分为3类[5]:基于解析模型、基于信号处理和基于知识经验的方法。目前应用最广泛的是基于信号处理的方法,其中主元分析(Principal Component Analysis,PCA)是一种基于信号处理的多元统计分析方法,在多变量高斯分布数据集建模方面具有出色的性能,已广泛应用于控制工程与故障诊断领域[6-8]。一些学者对PCA方法进行了改进[9-10],提高了PCA对故障的识别率,扩展了PCA方法的适用范围。已有学者尝试用PCA识别土木工程结构健康监测系统中传感器的故障,Hernandez-Garcia等[10]、胡顺仁等[11]将PCA方法应用于实际桥梁结构的传感器故障监测;Huang等[12]、Rao等[13]根据实验室模型获得的数据,采用PCA方法研究了传感器故障定位。
基于PCA原理,在传感器故障定位方面应用较多的是贡献图定位法[10-11],但传统贡献图定位法仅对故障期间某一时刻的数据进行分析,容易出现误判。其次,基于PCA的缺失变量法[12-13]虽能准确识别故障传感器,但针对监测系统中的每个传感器需循环计算,过程比较繁琐。另外,符号有向图法[14-15]能较好应用于各传感器之间有因果关系的监测系统,例如,化工、冶金工程等的传感器故障定位,但桥梁结构中各传感器的故障往往相互独立,因此,限制了该方法在桥梁结构健康监测系统中的应用。
综上所述,在土木工程领域,现有研究大多只分析一类或两类传感器故障,且只对单个传感器故障进行识别和定位,对两个或多个传感器同时发生故障的情况研究较少。同时,在桥梁结构健康监测系统中加速度传感器故障诊断的研究成果也较少。笔者通过改进现有的残差贡献图,提出累积残差贡献率指标,从而提高传感器故障定位的准确率,且可实现两个传感器同时发生故障时的定位,然后通过三跨连续梁数值算例验证方法的适用性。
1 PCA基本原理及故障检测
1.1 基本原理
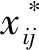
(1)
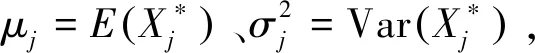
将处理后的m个传感器数据按列向量排列,组成n×m维的矩阵X,并计算X的协方差矩阵S。
(2)
S是一个m×m的矩阵,求出矩阵S的特征值λi和对应的特征向量Pi,并将特征值按从大到小排列,即λ1≥λ2≥…≥λm≥0。其中,Pi为第i主轴,其每个元素的值分别对应第i主轴与每条原坐标轴的夹角余弦值;λi表示矩阵X变换到Pi主轴后的方差。
令XPi=ti,ti为X在第i主轴的投影,表示第i主成分,也叫第i主元。矩阵X可表示为
(3)
通常采用特征值累积和百分比法确定所需的主元个数,较多文献建议取累积和达到85%[16]时确定主元个数k。
(4)
这样即能反应原始数据信息,又能达到降维的目的。确定主元个数k后,式(3)可写成
(5)
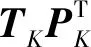
从以上过程可知,主元分析是一个降维的过程,降维的方法是通过基坐标向量的平移和旋转,把一个高维的信息投影到低维子空间,并保留主要信息。
1.2 故障检测
PCA的故障检测依赖于各传感器的相关性,若某一测点传感器发生故障,将会使之前建立起来的相关关系发生改变,造成统计指标数据异常。
PCA故障检测有两个统计指标,即HotellingT2统计量和SPE统计量。
在第i个时间点下,过程变量标准化数据为Xi,HotellingT2统计量定义为
(6)
式中:λ为主元特征值构成的对角矩阵;PK=[P1,P2,…,Pk],为主元特征向量构成的矩阵。
T2表示马氏距离,为Xi在主成分空间的投影点到主成分空间重心的距离。T2统计量的分布近似服从F分布,其控限可通过式(7)计算。
(7)
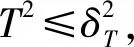
SPE统计量称为残差统计量,也叫Q统计量,定义为
(8)
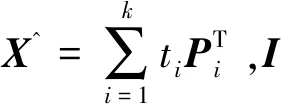
SPE表示欧氏距离,当检验水平为α时,可按式(9)确定其控限值Qα。
(9)
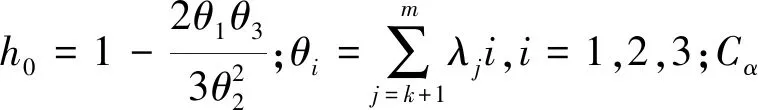
如果Q≤Qα,则传感器正常;如果Q>Qα,则传感器出现了故障。
2 累积残差贡献率法
已有研究[10]表明,SPE统计量对传感器故障更为敏感,在贡献图的基础上,提出累积残差贡献率指标。
2.1 残差贡献图
残差贡献图即采用某一时刻传感器数据的残差贡献值作图,其计算式为
(10)
式中:ei,j为第i时刻下第j传感器数据的残差,j=1,2,…,m。在残差贡献图中,可按照高贡献值的传感器即为故障传感器的原则[17]定位出故障传感器。
应该指出的是,贡献图有时不能准确定位故障传感器,主要是因为贡献图仅取故障产生的某一个时刻进行残差贡献值分析,但由于环境、外界激励的随机性,故障传感器会受到与之相关性较强的传感器的干扰,存在某些时刻正常传感器贡献值大于故障传感器的情况,容易得到错误的结果。文献[10]也指出,在某一时刻,正常传感器与故障传感器关联性可能较大,会对故障的定位造成干扰。因此,并非每个时刻故障传感器的贡献值都是最高,尤其是在多个传感器同时发生故障时,贡献图容易得出错误的结果,产生误判。
2.2 累积残差贡献率
虽然某个时刻故障传感器的残差贡献值不一定较大,但从统计意义上讲,其残差贡献值在一段时间内应总体偏大,故在传统贡献图的基础上提出了累积残差贡献率法。
首先,定义第i时刻j传感器数据的残差贡献率为
(11)
残差贡献率具有以下性质:
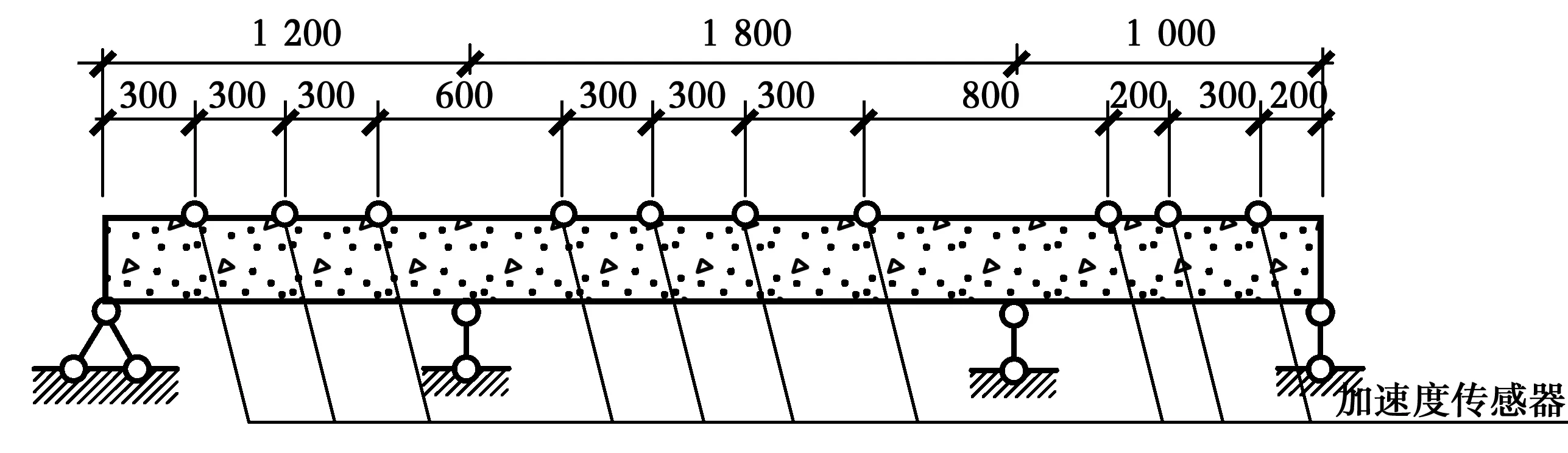
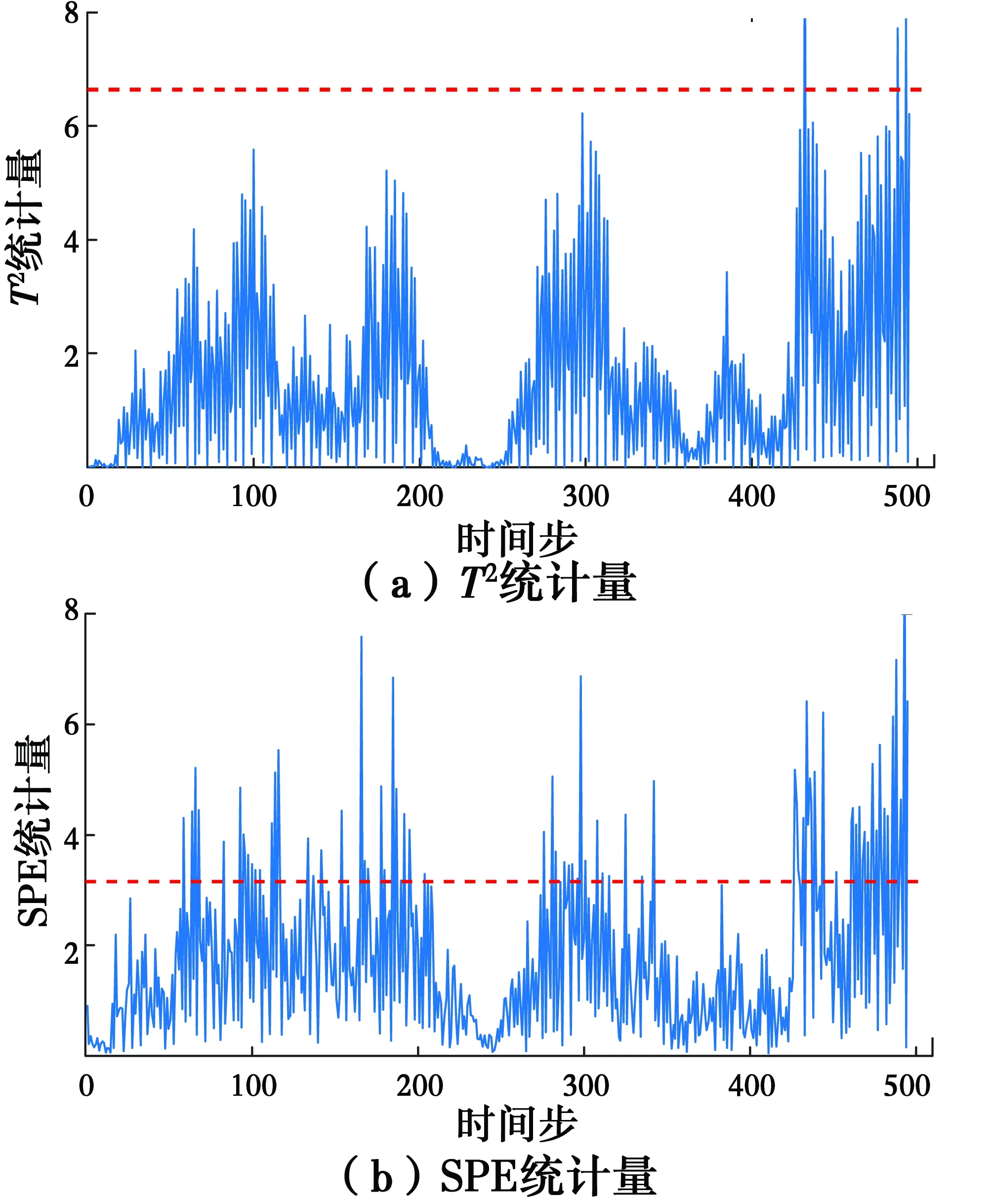
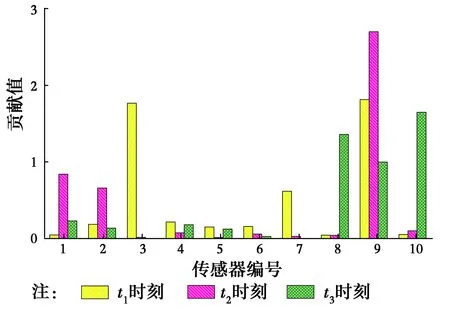
1)0 其次,分别计算故障时间段内N组数据的残差贡献率,并按式(12)进行加权,得到第j个传感器的累积残差贡献率。 (12) 最后,将各传感器的累积残差贡献率作图,按照累积残差贡献率指标明显偏大即为故障传感器的原则进行传感器故障定位。 累积残差贡献率图是对传统残差贡献图的改进,其保留了SPE统计量对传感器故障较为敏感的特性。相对于残差贡献图,累积残差贡献率图引入了统计概念,通过较长时间段内残差贡献值的加权平均来弱化某个时刻残差贡献值有偏差的情况,从而提高故障传感器定位精度。同时,累积残差贡献率将残差贡献值归一化到[0,1]之间,更有利于直观定位故障传感器。 传感器在正常工作过程中,不可避免地会受到噪声的干扰,所以,传感器返回来的数据与真实值有一定的偏差。用y*(t)表示t时刻被测变量的真实值,w(t)表示传感器测量噪声[4],则由传感器显示的正常值y(t)可以表示为 y(t)=y*(t)+w(t) (13) 当传感器的测量值与测量变量的真实值存在无法接受的偏差时,传感器被认为是有故障的。在传感器的7类故障中,白噪声卡死故障与零线漂移是卡死故障的特殊情况,精度下降是偏差故障的特殊情况。为节省篇幅,仅讨论更为广泛的4类故障。表1中列出了4种典型传感器故障的数学表达式,其中,a、b、c、f和G是描述相应传感器故障幅度的5个参数。 表1 4类典型的传感器故障数学表达式Table 1 Mathematical expressions of four typical sensor fault types 采用ANSYS软件建立三跨连续梁模型,模型的弹性模量E=3×1010N/m2,泊松比μ=0.3,密度ρ=2 500 kg/m3,模型尺寸为梁长40 m,截面为0.25 m×0.6 m的矩形。将三跨连续梁均分为200个单元,每个单元长度为0.2 m。采用白噪声地脉动作为连续梁的激励,使用Newmark-β法计算连续梁的加速度时程响应[18]。假设加速度传感器布设在距离左端支座3、6、9、15、18、21、25、33、35、38 m处,共计10个传感器,依次编号为1~10,如图1所示。 图1 三跨连续梁模型Fig.1 A Three-span continuous beam 试验过程中假设结构完好,仅传感器发生故障。首先生成115条均值为0、方差为1的随机白噪声作为地脉动激励,施加于结构。其中前100条结构响应数据用于PCA训练;第101至105条用于检验单个传感器发生恒增益故障的情况,记为工况1;第106至110条用于检验恒增益故障和固定偏差故障同时发生的情况,记为工况2;第111至115条用于检验卡死故障和固定偏差故障同时发生的情况,记为工况3,如表2所示。 根据参考文献[12,19]的建议,设置3种工况中各类传感器故障的幅度,如表2所示。 表2 3种传感器故障工况Table 2 Three kinds of sensor failure conditions 注:斜率f9满足在故障时间段内偏差故障从0线性增加到σ9。 假设三跨连续梁加速度传感器对每条地脉动波都采集100个数据,则每个样本的样本容量为100。传感器处于正常状态时共有100个训练样本,用于PCA训练,上述3种故障工况下各有5个不同的测试样本,这些采集到的样本数据均是真实值。 为模拟实际监测系统的环境干扰,在ANSYS计算的结构响应数据中加入噪声。根据Hernandez-Garcia等[10]、Huang等[12,19]的研究,实际监测系统中传感器的信噪比大致在15~25 dB之间,设置信噪比为20 dB,即噪声信号的均方根为真实信号均方根的10%。同时,为了更为真实地模拟现实环境中的有色噪声,首先产生10%均方根的白噪声,然后对白噪声进行有色处理,但为了避免数据失真,将有色噪声控制在均值为0,均方差为0.1σ的范围内。有色噪声的类型复杂,公式繁多,采用较为常见的有色噪声公式,令 Cn(t)=Wn(t)+0.5Wn(t-1) (14) 式中:Cn(t)为t时刻的有色噪声;Wn(t)为t时刻10%均方根的白噪声。按照式(4)在数值模拟得到的加速度中加入有色噪声,以此模拟传感器显示的正常数值,再进行PCA训练。传感器故障的输出信号按表1中的模型进行模拟。 在工况1下,经PCA检验后,其T2统计量与SPE统计量结果如图2所示,其中虚直线为各统计量置信度α=99%的阈值。从统计量的结果发现,虽然T2统计量没有超限,但SPE统计量存在大量超限的点,超限率为15.56%,达到了规定限值,可以判断该过程中存在故障。 T2统计量检测的是主元空间的数据变动,SPE统计量检测的是残差空间的数据变动。从图2可知,在传感器故障检测中,T2统计量不如SPE统计量敏感,对传感器故障数据的识别较差。所以,在下文的故障识别与定位过程中,仅讨论SPE统计量及其改进的累积残差贡献率。 随机选取3个时刻,记为t1、t2和t3,作这3个时刻的残差贡献值图,如图3所示。从该图可知,t1时刻5号传感器的贡献值最高,可以正确定位出5号传感器为故障传感器,但在t2和t3时刻并不是5号传感器的贡献值最高,出现了误判现象。 图2 工况1下PCA检验统计量Fig.2 PCA test statistics result of condition 图3 工况1某一时刻残差贡献值Fig.3 residual contribution value of condition 采用该方法,作累积残差贡献率图如图4所示。该图显示5号传感器的累积残差贡献率最高,故可以正确定位故障传感器。 图4 工况1累积残差贡献率Fig.4 Accumulated residual contribution rate of condition 为讨论累积次数N对故障定位的影响,计算不同N下累积残差贡献率如图5所示,图中1~10表示传感器的编号。由该图可知,累积超过50个时间步之后,故障传感器的累积残差贡献率开始突出,其他传感器的贡献率开始弱化。累积次数超过100次后,各传感器的累积残差贡献率趋于稳定。因此,为了准确定位故障传感器且减少计算时间,建议累积次数N取值为100。 图5 不同累积次数对故障定位的影响Fig.5 The relationship between cumulative residual contribution rate and cumulative 在工况2下,SPE统计量的超限率为31.11%, 随机选择3个时刻,分别命名为t1、t2、t3,作这3个时刻的残差贡献值图如图6所示。从图6可知,t1时刻4号和8号传感器的贡献值远大于其他传感器,可以定位出这两个传感器发生故障;但t2时刻8号传感器和10号传感器的贡献值较大,出现了错判;t3时刻仅能判断出4号传感器发生了故障。因此,传统的贡献图法在多传感器同时发生故障时更容易出现误判。 采用累积残差贡献率作图如图7所示,4号传感器和8号传感器的累积残差贡献率远大于其他传感器的累积残差贡献率,可以判断这两个传感器发生了故障。 图6 工况2某一时刻残差贡献值Fig.6 residual contribution value of condition 图7 工况2累积残差贡献率Fig.7 Accumulated residual contribution rate of condition 在工况3下,经PCA检验后,其SPE统计量的超限率为13.3%,故可判断有传感器故障发生。随机选取3个时刻作残差贡献值图如图8所示,累积残差贡献率图如图9所示。图8和图9表明,传统的残差贡献值法定位存在误判情况,而累积残差贡献率能够准确定位出发生故障的传感器。 图8 工况3某一时刻残差贡献值Fig.8 residual contribution value of condition 图9 工况3累积残差贡献率Fig.9 Accumulated residual contribution rate of condition 针对实际结构健康监测系统中传感器可能发生故障而影响后期结构安全评估的问题,在传统残差贡献图法的基础上,基于统计原理提出了累积残差贡献率法,数值模拟算例表明: 1)主元分析的SPE统计量能识别出传感器故障,说明在传感器故障识别中SPE统计量比T2统计量更为敏感,这与已有文献的结论一致。 2)累积残差贡献率将残差贡献值归一化到[0,1]之间,更有利于直观定位故障传感器。无论是单传感器损坏还是两个传感器损坏,该方法较传统贡献图法能更准确地定位故障传感器。 3)累积残差贡献率通过对故障时间段的残差贡献率进行加权平均,提高了故障定位的精度。累积的故障时间越长,故障定位越准确,为了准确定位故障传感器且减少计算时间,建议累积次数N取值为100。 应该说明的是,笔者在验证所提方法的过程中,假设结构完好,仅传感器发生故障。这主要是因为实际工程结构的损伤通常是累积损伤,需多月或多年才有明显的变化,而传感器发生故障的时间尺度远小于结构损伤的时间跨度。但如何分离传感器自身故障和结构损伤仍需今后进一步研究。3 传感器故障模型

4 数值模拟分析

4.1 单传感器故障定位
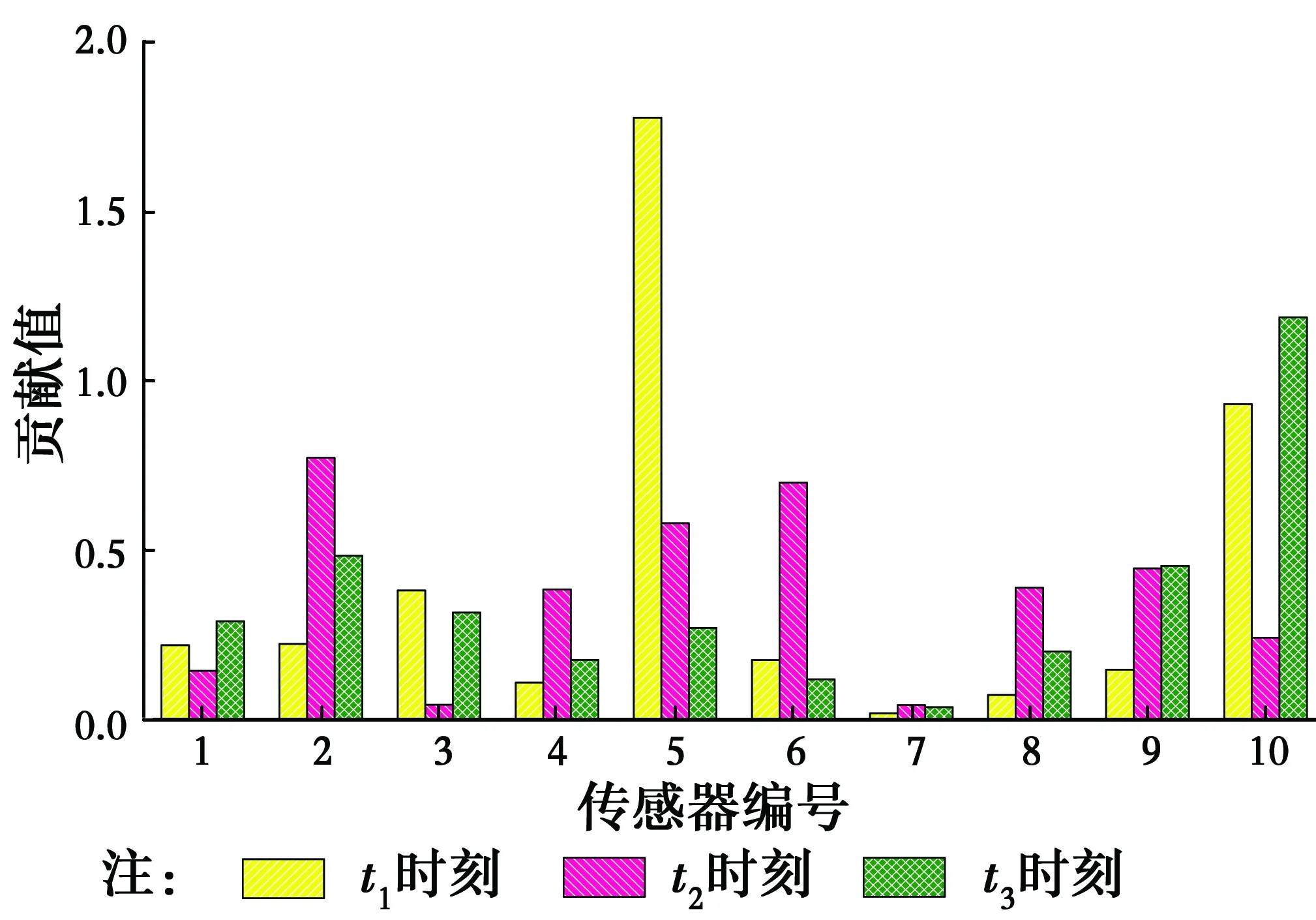
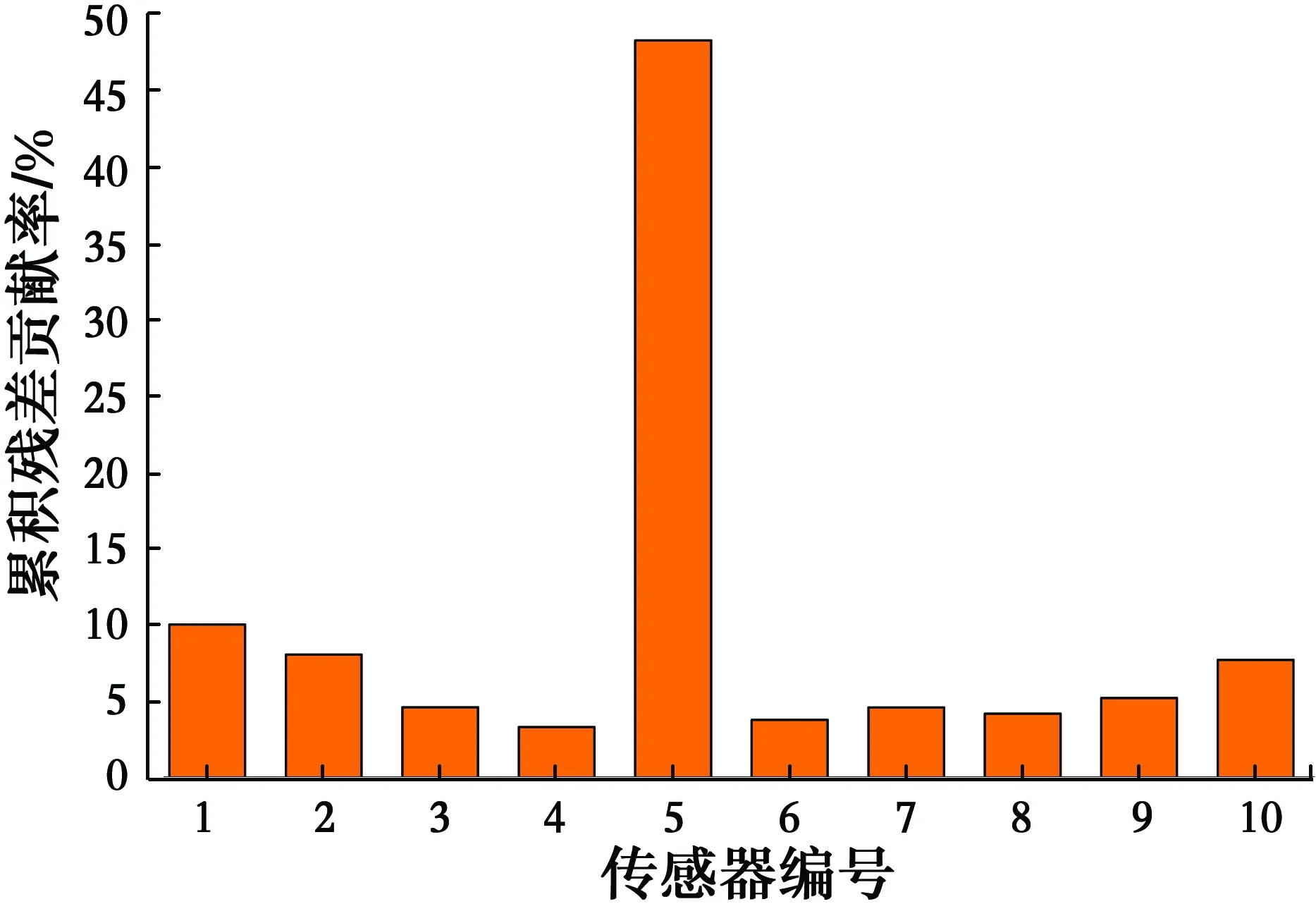
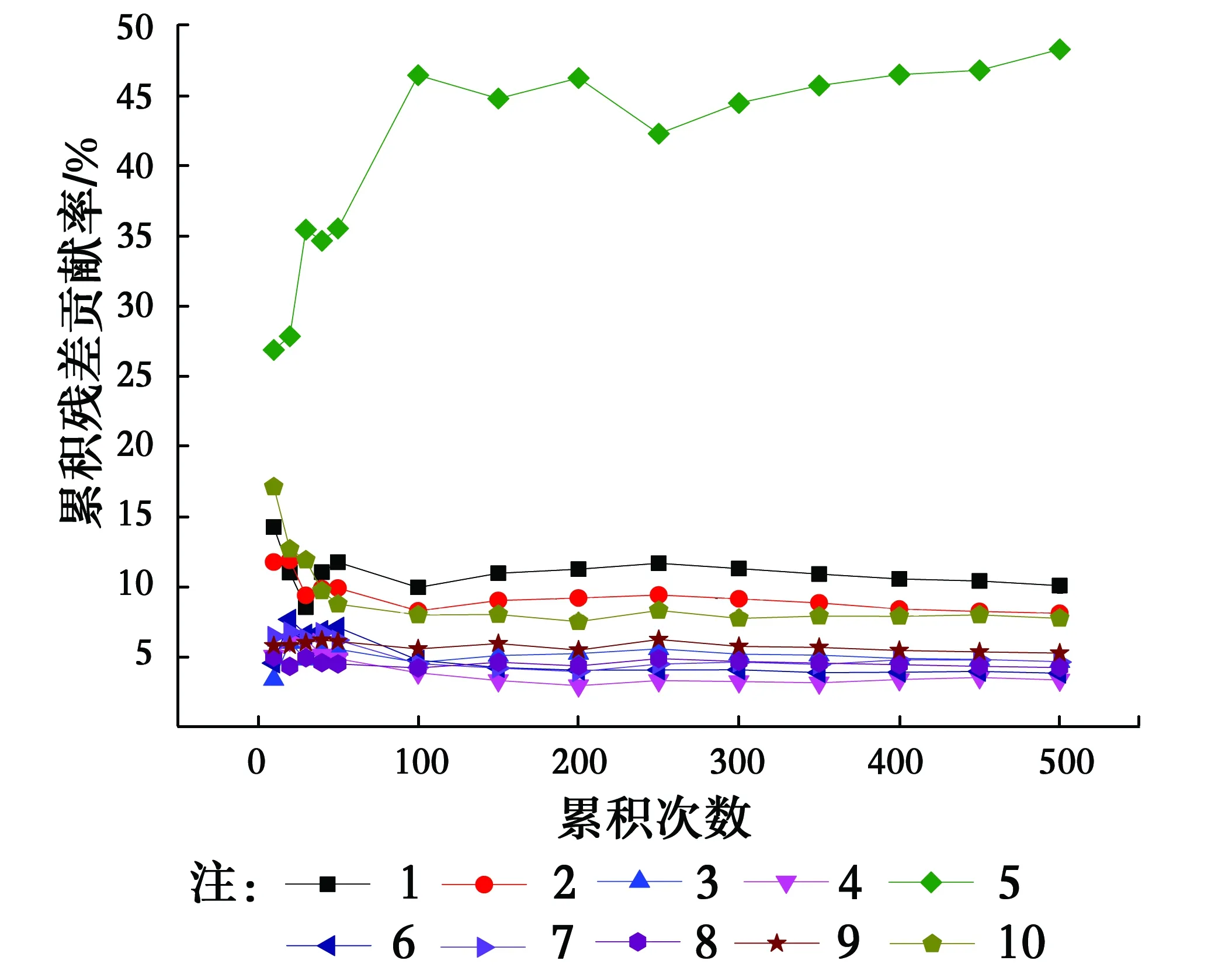
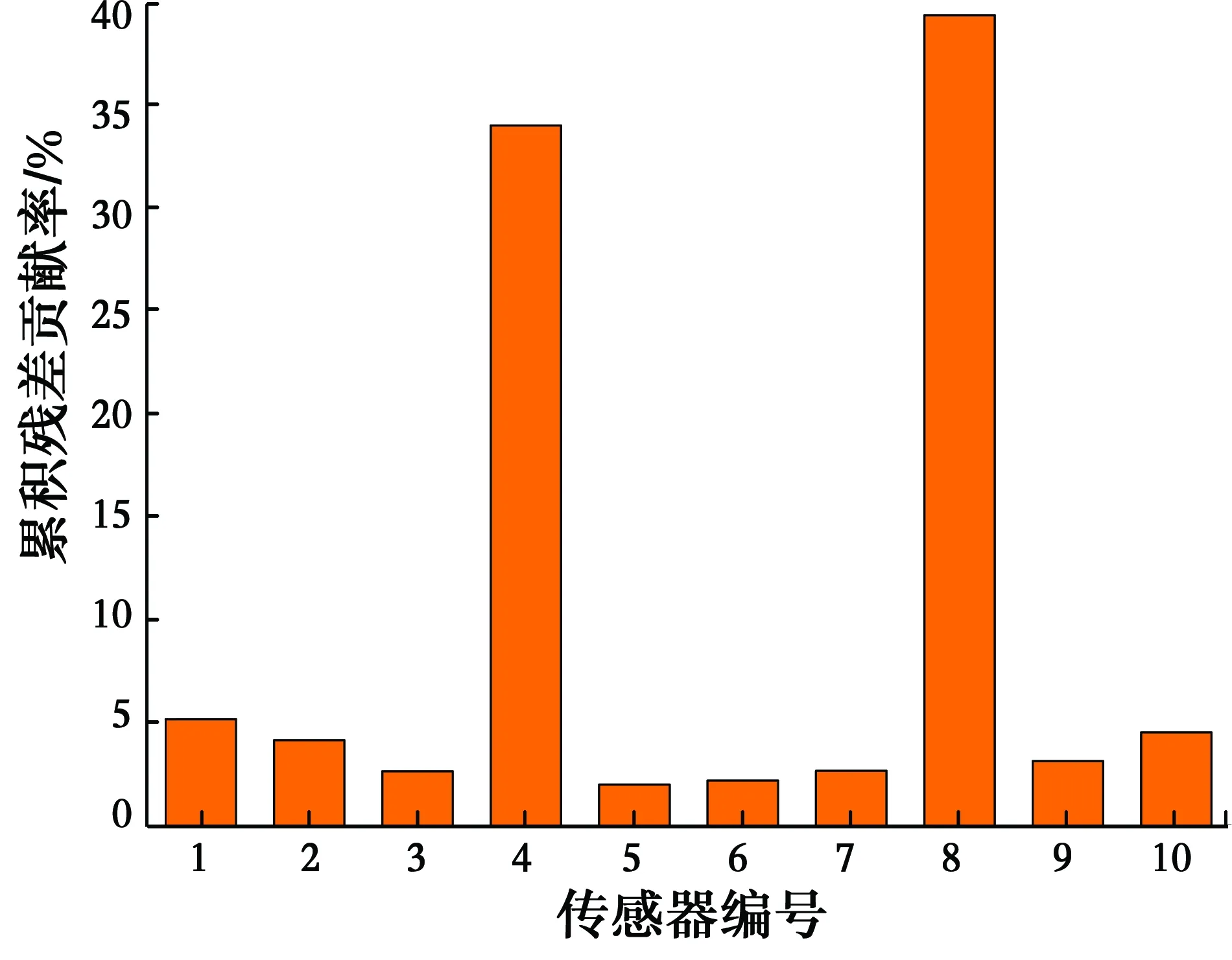
4.2 两传感器故障定位


5 结论

