露天矿计划阶段内离散块体物料运距预测算法

柴森霖，刘光伟,2，白润才，曹 博,2

(1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000; 2.辽宁工程技术大学 煤炭资源安全开采与洁净利用工程研究中心,辽宁 阜新 123000; 3.辽宁工程技术大学 辽宁省高等学校矿产资源开发利用技术及装备研究院,辽宁 阜新 123000)

矿岩运距是衡量露天矿山卡车运输经济性的重要指标之一[1-3]，同时也是优化开拓运输系统运营成本的重要基础，对矿山开拓运输系统优化建模、最佳调运方案配置以及优化运输成本等研究均具有重要意义。

目前，有关矿岩运距计算方法的研究可大致分为两类:第1类是利用阶段性道路网络设计，结合重心算法对物料进行分岩种、分水平、分块段的几何量测[2,4-12];此类方法被广泛应用在进度计划方案优选、矿山运输系统优化以及物料流规划建模等相关研究领域，如张幼蒂教授针对矿岩流向、流量优化模型，提出的阶段性运输网络中运距计算方法[2];又如赵景昌等为建立以运输功最小化为优化目标的物料流规划模型，以年为时间单位划分阶段，并结合阶段性运输道路网络图进行运距量测[4]。第2类是采用奇偶点法计算有向图多边形面积，通过多边形面积变化率映射排土场排弃量与运距之间动态关系(S=F(v)曲线)[1,13-14];此类方法被应用于排土场运距推估等相关研究领域，如张瑞新教授等根据累计物料量变化率受形状约束的特性，提出一种利用排弃物料量动态推估运距的方法[13];刘光等利用计算机模拟技术，总结出推估并绘制S=F(v)曲线的基本流程[14]。

笔者在前人研究成果的基础上，根据外排土场出入口服务周期长、年度计划阶段内运输线路具有相对稳定等特点，针对阶段性道路网络无法描述逐条带的路线波动、直接逐条带推估离散块体运距困难且在物料规划场景中不现实等问题展开研究，提出外排土场计划阶段内离散块体过程运距动态赋值的新方法，其基本思想即利用关键的运距影响因素，建立一组动态的非线性预测模型，并利用年末排土计划位置上路网提取运距属性信息，训练预测模型、优化确定非线性模型参数。最终，应用运距的非线性表达对年度排土计划阶段内的离散块体物料进行运距赋值。经仿真对比实验验证，所述算法模型对解决计划阶段内的逐条带块体运距赋值问题具有现实有效性。

1 WLS-SVM模型计算理论

支持向量机(Square Vector Machines,SVM)是数据挖掘算法中一种新颖的小样本统计学习方法，由Corinna和Vapnik等于1995年提出，主要用于解决小样本、非线性及高维模式识别中，后被推广应用到函数拟合等其他机器学习问题中。加权最小二乘支持向量机(Weighted Least Square Vector Machines,WLS-SVM)是在SVM及LS-SVM(Least Square Vector Machines，LS-SVM)基础发展起来的，保留了算法模型中的平方误差损失以及等式约束等特性，消除了异方差性，具有更好的学习能力、泛化能力，预测准确率更高[15]。

对于给定运距预测模型的训练集合{(xk,yk)|k=1,2,…,N}，其中xk为p维的参数样本，yk为样本输出集，则该问题的凸二次优化模型[16]可表述为

(1)

约束条件为

s.t.yi=ωTφ(xi)+b+ei

(2)

式中，ω为权系数向量;e为误差集;φ(xi)为输入参数到希尔伯特空间的映射;C为惩罚因子;b为模型阀值;ei为样本误差;λi为误差权值。

根据式(1)，(2)中优化模型采用拉格朗日算子法进行求解，建立二次凸优化对偶模型如下:

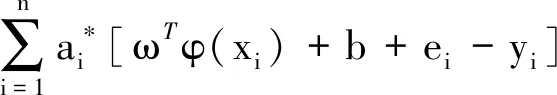
(3)

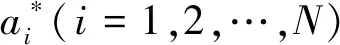
对式(3)采用偏导极值法求解，消除偏导方程组中的无关变量ω，ei，化简为如式(4)的线性方程组，等价问题即为求解方程组中的未知变量a*和b，矩阵求解形式如式(5)所示:

(4)

(5)

根据优化条件引入径向基核函数，最终获得的回归估计函数如式(6)所示，其模型基本结构如图1所示。

(6)

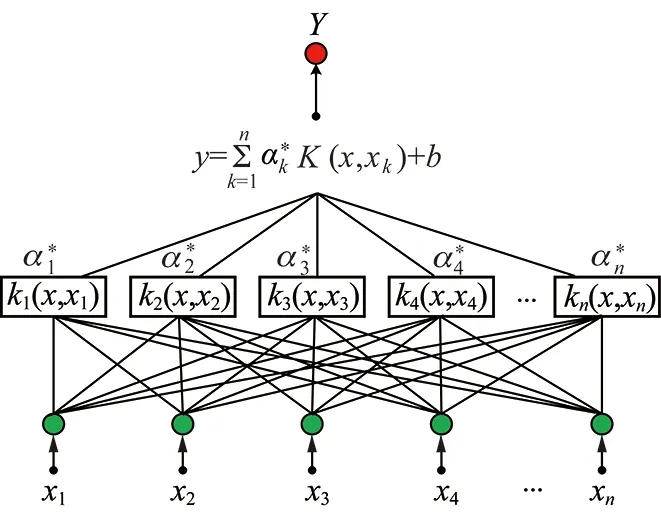
图1 WLS-SVM 基本结构示意Fig.1 Structure of WLS-SVM

2 离散物料块体运距预测模型

2.1 模型适应性分析

露天矿外排土运距主要由采场运距、运输干线长度以及外排土场内部运距3部分组成，其中因排土干线长度相对固定，而采场运距和排土场内部运距则易受道路网络在条带间的动态变化，而产生较为明显的波动效应。从运输道路设计角度分析此种波动效应可发现，采场道路设计因受煤层起伏、台阶并段等因素限制，特别是当工作帮线路采用移动坑线设计时，运输线路灵活，易造成计划阶段内运输线路存在差别于计划工程位置上的结构性变化，导致阶段内线路的动态发展趋势不可控，无法实现预测性动态推估。但区别于采场运输线路，外排土场内部运输线路则通常设有特定入口或特定干线，道路多为固定或半固定线路，服务周期长于采场内部的采场线路，阶段内干线动态演变趋势仍保持计划工程位置上运输线路的结构特性。因此，采用特定模型即可实现近似预测性的动态推演。

2.2 外排土场运距影响因子选取

露天矿外排土场运输网络是一种非线性动态系统，其运距预测精度则明显受道路运输系统的关键组成要素的影响，即受到文中非线性模型的输入参数控制，但通常这些因素之间存在内在的联系，即使我们采用特定的降维策略，其输入参数维度依然会对拟合造成一定的影响。故为进一步从众多存在特定内在联系的影响因素中确定外排土场运距的关键影响因素，降低模型输入参数维度，本文采用主成分分析中压缩冗余成分的策略来处理和优化上述输入参数维度，以消除冗余因素来提高预测模型精度。基于此，我们首先建立运距影响因子的内部依赖关系分析模型，初步选取块体质心至排土场入口的欧氏距离(D如式(7)所示)、物料提升高度(H)、阶段累加工程量(M)、坡道长度(L)、缓冲段长度(L′)、台阶高度(HT)以及道路坡度(β)、块体长(l)、块体宽(b)、块体高(h)、排土工作线长度(R)、排土平盘宽度(B)等12个影响因子建立因子分析模型，将上述12组影响因子作为12种分析成分，按照1～12编号代入SPSS软件内置的因子分析模型，计算相关系数矩阵的特征根及方差贡献率，并按照特征值排序后统计见表1。

表1 因子及贡献率Table 1 Factors and contribution rates

(7)

为避免维度过高且有效保留因素中样本数据的内在特征，文中以因子特征值大于1和累计贡献率范围在70%～85%为降维标准，最终选取前7个指标参数作为运距预测模型的输入参数:D(km)、H(m)，M(万Mm3)，L(m)，L′(m)，HT(m)，β(°)。

2.3 模型评价因子设计

运距预测模型的误差水平是评价整个预测模型精度的重要指标，为综合评价算法模型中参数优化和运距预测效果，文中在传统的均方误差、拟合优度、绝对误差期望、相对误差期望等误差评价指标基础之上，引入无量纲的错估计系数，利用此系数评价绝对误差大于推估块体最小边长的规模程度，其误差评价判据如式(8)所示。评价体系中认为这种误差会直接影响推估块体的运距计算精度，其参数计算方法如式(9)所示:

eME=y′-y>lmin

(8)

(9)

式中，eME为绝对误差；l为块体模型边长；y′为运距的估计值；y为运距训练值；nM满足错误估计判据的块体模型数量；n为总体块体数量。

2.4 参数优化模型

2.4.1WLS-SVM模型的权值改进

对最小二乘回归估计模型引入权向量是为有效削弱异常数据造成的离群误差波动，增强回归模型整体稳健性[17]。因此，权向量的优化选择对于提高运距预测模型精度意义重大。通常，权向量的确定多采用权函数赋值方法，其中常见的权函数如线性权函数[17]或改进的正态分布权函数[18]等。此类方法应用简单、方便，但均为主观修正，会受到过滤条件等因素的影响，造成一定程度的精度损失。因此，为保证运距预测模型具有更好的离群误差控制能力，笔者在自适应正态分布权函数[18](图2中曲线BDFGH、曲线BDEGH)的基础上，提出一种改进的区间自适应权函数，其权函数如式(10)所示，函数形态如如图2中曲线ACEGH所示。

(10)

(11)

图2中ζr,m,ζd分别为由点D，E，G切分而成的权向量配重区间节点，区间1，4分别为低误差和高误差区域，自适应函数会对此部分进行调节，保证改造后的权值模型能有效改善误差集内的权重分配，将较大权重自适应的赋值给区间1;而区间2，3为区域中值分布区域，区间2相对误差更小，因此曲线保持反比例正态特性，而区间3误差是偏离中值，随偏离程度加大，正态特性则会压缩中值，赋予较低权重。

图2 权值函数形态示意Fig.2 Weight function diagram

在上述曲线模型定义的基础上，为进一步说明权重修正过程，文中给出权重自适应动态修正的流程如图3所示。其中u1，u2分别用来控制正态分布函数形态，权重配比空间被分割后，随着迭代进行误差较大的样本会因为权重影响而被滤除，故随算法迭代轴线EF会不断向AB侧移动，实现动态的自适应调节配权，进一步提高预测模型精度。

图3 权函数动态修正流程Fig.3 Weight function dynamic correction flow chart

2.4.2基于改进粒子群算法的模型优化调参

应用支持向量机进行回归估计是基于传统求解不适定问题的思想，通过引入核函数以实现标准算子方程向正则化泛函的转化，并完成对高维空间算子方程的求解，其核函数的质量直接关系到非线性预测模型训练速度及泛化能力[19-20]。因此，为提高非线性运距预测模型的拟合精度及收敛速度，笔者采用粒子群算法(PSO)进行核参数优化，以参数c,σ为平面粒子位置坐标，建立线性优化模型如式(11)所示，将式(12)作为优化粒子群算法的适应值函数。

(11)

(12)

另一方面，考虑模型易受训练数据规模局限性以及其他多种综合因素限制，且上述影响对粒子群算法极为敏感，严重制约粒子群算法种群的搜索范围，导致随着迭代进行会促进种群丧失多样性，极易造成迭代初期算法便出现早熟现象。为使算法在迭代初期具有较强的空间搜索能力，在迭代后期具有较强的寻优能力，对粒子群状态转移模型中的惯性因子(w)、学习因子(c1,c2)进行了如式(13)的修正。此种修正的作用在于能有效的保证算法在迭代初期以较大的范围搜索最优解，保持种群多样性;在迭代后期能实现更精细的局部搜索，以提高整体优化建模精度。

(13)

式中，ws,we分别为惯性权重w的初始值和上一期迭代结果值;c1s，c1e分别为学习因子c1的初始值和上一期迭代结果值;k为迭代次数;G为总的迭代次数。

最后，为进一步扩大粒子搜索空间，减少个体寻优过程中易陷入局部最优状态的可能，在每次迭代产生的搜索空间内，算法会采用轮盘赌法随机调整部分粒子位置，其位置更新模型如式(14)所示:

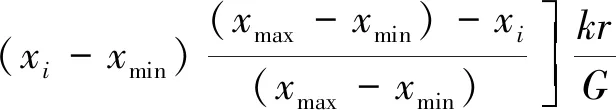
(14)

式中，r为[-1,1]区间上的随机数;xmax,xmin为粒子位置的区间边界。

其轮盘赌概率事件模型如式(15)所示。

(15)

2.5 外排土场运距预测模型算法流程设计

基于MPSO-WLS-SVM的运距预测算法基本流程如图4所示，其核心作用是将WLS-SVM模型、权向量修正以及MPSO有机的结合起来，通过相互之间的动态调配，最终实现运距的理想输出。

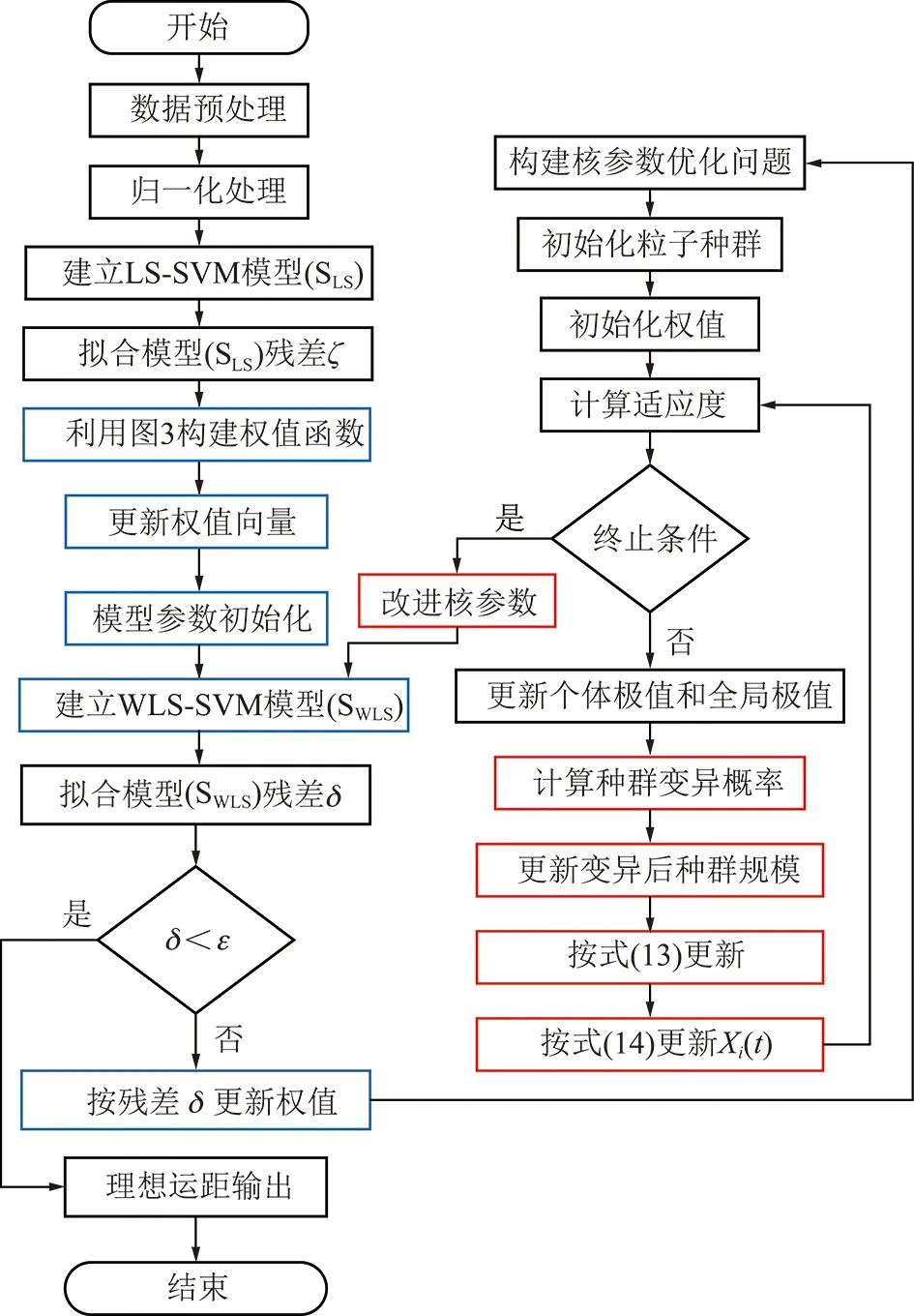
图4 运距预测算法流程Fig.4 Flow chart of haul distance prediction algorithm

其算法具体实现步骤如下:

(1)因各影响因子的量纲和取值范围不一致，为进一步提高算法的收敛速度，对影响因子进行线性归一化处理，利用式(16)将影响因子统一映射到[0,1]区间内;

(16)

(2)拟合普通最小二乘支持向量机回归估计模型残差;

(3)根据残差值和权值函数反求加权最小二乘模型权重初值;

(4)引入核参数初值，用以构建基础核参数优化修正迭代模型;

(5)利用步骤(3)中求得的权重以及核参数初值，建立待优化参数的初始WLS-SVM模型;

(6)拟合WLS-SVM模型残差，建立参数优化质量评价指标;

(7)评价体系指标，如果小于阀值向量即得到动态理想输出，否则修正WLS-SVM模型权值向量，开始迭代反向修正核参数;

(8)利用MPSO模型修正核参数，保证当前权重模型下训练模型的核参数动态最优解;

(9)将MPSO修正结果代入步骤(4)进行动态迭代，直至步骤(7)中获得理想的运距输出，算法结束。

3 模型检验及实例

研究以构建黑山露天矿物料流规划模型为背景，并为解决物料流能耗模型中无法实现逐块体运距推估问题展开。选取该矿2018—2019年南部卡车外排土场年末计划位置图为基础数据采集模型，收集了计划工程 位置上的300组块体模型的设计数据进行建模分析和预测，块体模型标准尺寸85×50×20，块体具有次级结构尺寸;采用随机抽样选取100组数据作为预测模型的训练样本集，其中50组来自于2018年排土计划工程位置，其余50组来自于2019年排土计划工程位置;并选取剩余中的50组作为测试样本集。设置WLS-SVM和MPSO模型初值如下:c0=3.5,σ0=0.5;种群规模N=30，最大迭代次数G=300，c1=2.5,c2=0.5,w=1。

3.1 算法拟合精度及预测效果评价

3.1.1算法模型拟合精度评价

为验证改进的参数优化算法对模型拟合精度和收敛性的优化效果，分别建立MPSO-WLS-SVM,PSO-WLS-SVM,WLS-SVM和MPSO-LS-SVM四组模型拟合训练数据，受篇幅影响仅提供100组训练集的部分数据见表2。为突出参数优化效果，对4组模型的绝对误差进行统计,其统计结果如图5所示。

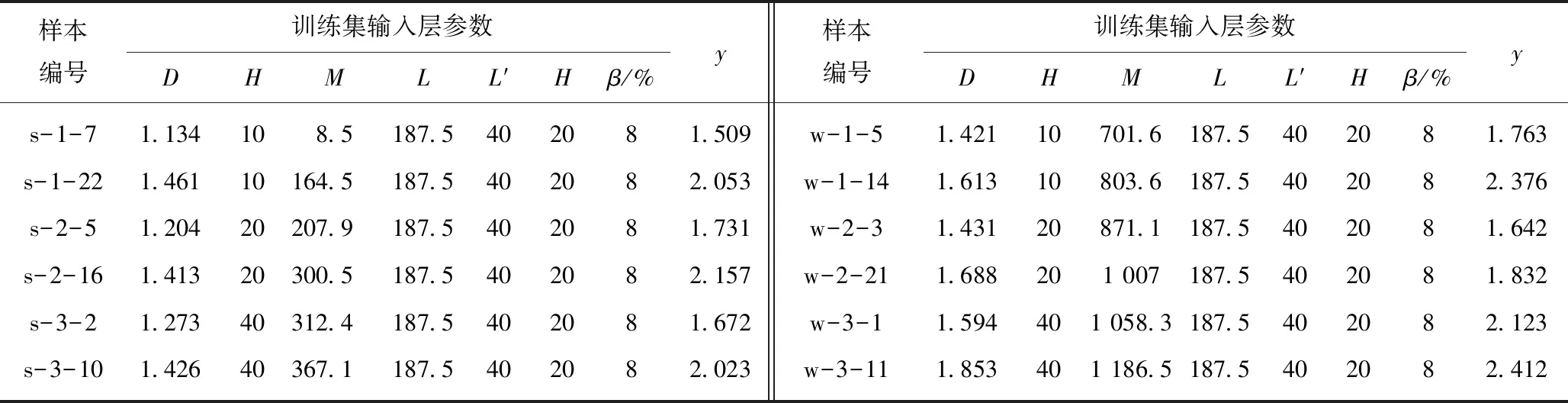
表2 MPSO-WLS-SVM模型输入输出训练数据集(部分)Table 2 Input and output training data set on MPSO-WLS-SVM

注:s-x-x第1位表示年份，第2位表示所处台阶，第3位表示块体位置，s代表2017年，w代表2018年。

由图5可知，100训练样本中MPSO-WLS-SVM模型(红色曲线)拟合精度最高。较之MPSO-LS-SVM模型，引进的动态权值能有效的控制离群误差规模，提高了预测模型精度。而较之PSO-WLS-SVM、WLS-SVM模型，基于MPSO模型的核参数优化具有更高的拟合精度和收敛速度。

对于实际物料流规划问题，其绝对误差小于错估计指标即认为对规划问题能耗没有本质上的影响。因此，为进一步验证MPSO-WLS-SVM模型预测算法稳健性采用测试集数据设计了5组重复试验，并统计错估计系数如图6所示。对比图中结果，当样本规模较小时，预测错估率较高，且随样本规模增大误差趋于稳定。自样本规模N>90开始算法模型拟合精度随样本规模趋于平稳，最终错估系数稳定在0.8%～1.2%，算法具有良好的稳健性。

图5 训练集绝对误差对比Fig.5 Training set absolute error comparison diagram

3.1.2测试集运距预测效果评价

将50组测试集数据代入优化调参后的预测模型中，其运距预测仿真对比数据见表3(受篇幅限制仅提供部分数据)，详细的预测数据输出结果如图7所示，其中左侧主轴为预测结果与真值对比，右侧次轴为预测模型绝对误差统计。

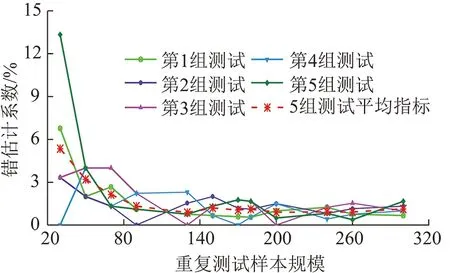
图6 5组重复试验错估系数统计Fig.6 Miscalculation coefficient of line chart on Repeat 5 times

表3 仿真测试数据模型输入输出层参数样本(部分)Table 3 Simulation model input and output layer parameter test data samples(the part)

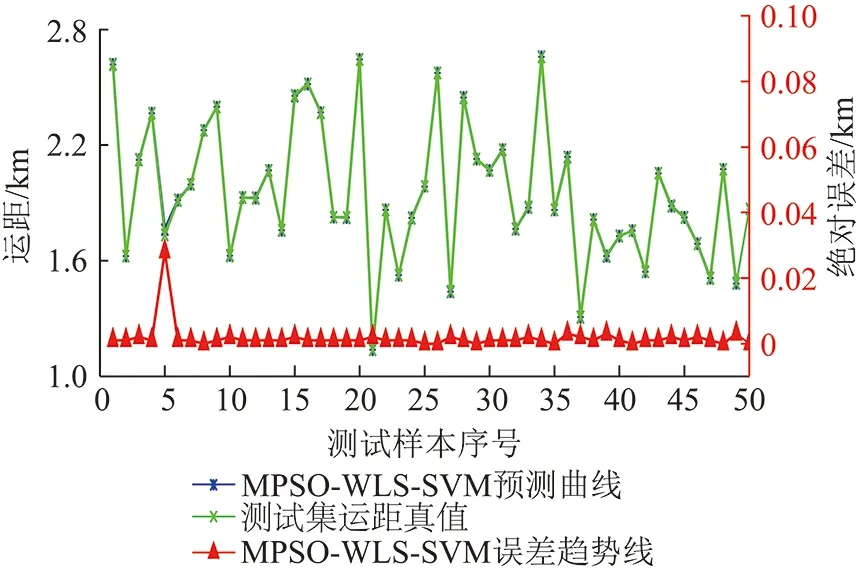
图7 MPSO-WLS-SVM测试集仿真预测结果Fig.7 Test set simulation results to MPSO-WLS-SVM

由图7中测试集预测结果与真值对比可知，算法仿真测试具有较好的拟合精度，50组预测估计中仅第5组测试数据绝对误差大于20 m，存在错估现象，其余拟合精度均控制在错估计误差以下，且误差限变化平稳，收敛速度较快，具有较强的泛化能力，其预测效果能满足运距预测建模需求。

3.1.3算法预测效果对比评价

为进一步验证MPSO-WLS-SVM模型在运距预测方面的优势，本文从参数优化对算法执行效率的改善以及同类算法预测效果对比等2个方面对算法的实际应用效果进行综合评价。其中针对算法执行效率的评价设计了4组不同样本规模的仿真实验，即M1模型—普通正态权重的WLS-SVM模型、M2模型—改进权重WLS-SVM模型、M3模型—PSO改进M2模型(PSO算法采用经典模型中的固定参数c1=2.5,c2=0.5,w=1.3)以及M4模型—MPSO改进M2模型，统计各组模型在不同样本规模下多次重复实验的平均收敛时间如图8所示。

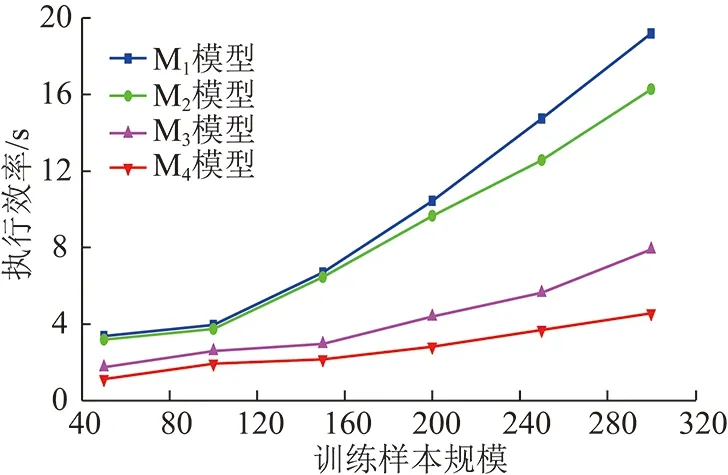
图8 参数优化后执行效率对比Fig.8 Performance comparison after parameter optimization

对比图8中M1和M2模型可发现，文中引入的自适应权重修正策略，能在一定程度上提高算法执行效率，但并不明显，随着样本规模逐渐变大，收敛时间呈指数增长;当引入群智能算法后，能大幅度提高算法的收敛效率，且图8中随迭代进行，后期效率能得到成倍提升;通过对比M3与M4模型收敛效率，可以看出在不同时期调节惯性因子和学习因子对于提高种群多样性的确有促进作用，能有效提高算法的执行效率。

另一方面，为体现文中算法在处理此类问题中的优越性，文中分别选取BP模型、SVR模型、GA-BP模型以及GA-ELM模型进行算法对比，并统计绝对误差以及整体预测效果见表3。

由表4中5组评价因子对比可知，两组GA模型执行效率分别为1.41 s和1.24 s，执行效率明显优于文中模型;MPSO-WLS-SVM模型精度评价指标分别为:均方误差为 0.008 8;相关系数为 0.99;平均相对误差为 0.047%;平均绝对误差期望为0.84，对比其他模型具有更高的拟合精度和预测效果。对比表4中预测效果，MPSO-WLS-SVM模型预测效果均优于其他4组对比模型，(a)，(c)两组次之。(a)～(d) 4组预测模型误差波动较大，其主要原因在于受离群数据的影响较为严重，4组算法均无法有效的过滤离群数据提高拟合精度，(c)，(d)模型中应用的遗传算法优化反而增加了离群误差的波动，造成预测结果进一步恶化。鉴于此，文中方法具有更强的离群误差处理和学习能力，预测效果更好。

表4 不同算法模型预测效果测试样本结果比较Table 4 Comparison of different model effects

3.2 物料流能耗模型精度评价

外排土场时变运距预测模型拟解决的本质问题即为提高堆置次序优化模型中运输功能耗表达的精度。因此，为进一步说明运距预测算法对于改善能耗模型的有效性，研究以黑山露天矿2018—2019年期间南部卡车排土场六组排土条带为研究对象，并逐条带建立物料块体的运输联系，最终以上述六组条带内块体计算出的总运输功为精度评价标准，对比分析采用阶段内分水平、分区段运距几何量测方法以及文中算法所建立的物料流能耗模型，对比结果如图9所示。由图9可知，采用文中算法建立的运输功能耗模型更接近逐条带运输系统设计方案，较之基于阶段间分水平、分区段的年度物料量运输推估方法，总运输功计算精度更高。

图9 运输功能耗对比Fig.9 Comparison diagram of transport work

4 结 论

(1)在采用加权最小二乘模型建立多元非线性运距预测模型的基础上，论证了预测模型对于推估外排土场物料块体运距的现实有效性，并进一步通过引进加权最小二乘模型权向量修正、核参数动态调参等优化手段，改善了运距模型自身的稳健性，有效的提高了运距预测准确率。

(2)通过不同参数优化策略的对比实验分析，验证了文中提出的权向量动态修正算法、基于改进粒子群算法的核参数优化方法，对于改进算法自身缺陷具有显著效果。

(3)对比其他智能优化算法，验证了文中算法模型预测精度更高，受训练样本规模干扰小，且当N>90时，错估计系数期望值即可稳定在0.8%～1.2%，具有良好的稳健性，可为建立精准的运输功能耗模型提供有力的基础数据支撑。

(4)预测算法为保证多种优化手段间达到全局最优效果，通过适应值函数建立了权向量修正与径向基核函数调参的动态联系，此法有效的提高了模型精度，但其迭代过程时间成本较高，训练周期长，连续的多阶段预测效率相对较低。因此，笔者下一步将引入一定的启发式策略改进算法，加快迭代过程。