潜载随动系统的扰动特征与复合轴补偿机理研究

刘宗凯， 陆金磊， 薄煜明， 王军， 汤兆烈

(1.南京理工大学 先进固体激光工业和信息化部重点实验室， 江苏 南京 210094;2.南京理工大学 瞬态物理国家重点实验室， 江苏 南京 210094)

0 引言

潜载激光武器是未来研究的一个方向，由于激光武器需要引导激光持续稳定地照射在目标位置，其跟瞄系统的稳定跟踪精度需要比常规光电随动系统高1～2个数量级，从而给潜载激光武器的随动控制提出了更高的要求。潜载光电桅杆最初只搭载潜望镜，但随着科技的进步其逐渐成为以计算机为控制核心的高级光电成像与自动跟踪控制系统，也是光电系统现代化的突出代表。它是水下潜艇实现水面目视观察、激光测距、导航制导、激光通信、光学跟踪等多种功能的设备[1-2]，也是未来潜载激光武器的重要平台。

流体流过有限长物体时，物体两侧的压力差会导致流体从压力面向吸力面流动，从而形成梢涡，工程上最常见的梢涡出现在飞行器翼端和水下潜航器端部。梢涡有很多负面影响：在水动力学方面，在梢涡涡心区域会产生较大的低压区，当压力降低到一定程度时会产生空化点蚀；此外，梢涡的强烈脉动会产生振动和噪声，对水下潜艇的稳定性和隐蔽性极其不利，而且这些扰动最终会反映到视轴坐标系上，从而制约跟瞄系统精度的提升[3](见图1)。

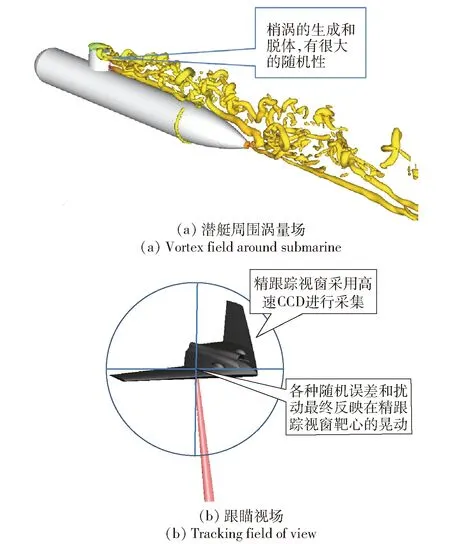
图1 潜艇涡激振动对光轴稳定的影响Fig.1 Influence of vortex induced vibration on optical axis stability

文献[4]通过潜艇模型实验分析了梢涡的振荡，结果表明梢涡振荡幅度在近尾缘处并不显著，在向下游发展的过程中其振幅随着距离呈线性增长[5]。Kim等[6]用流体力学分析软件SUBFLO_2和Fluent计算了美国国防高级研究项目局SUBOFF型裸艇体、裸艇体加围壳和裸艇体加尾舵3种模型在0°～20°偏航角时水动力和力矩的演变特征。Vaz等[7]分析了附体结构对潜艇受力和流场演化的扰动，发现强制上仰过程中潜艇会产生较大的力矩延迟和波动，这些扰动极大地增加了潜载跟瞄装置的角跟踪误差[8]，对于有更高精度要求的激光武器，需要结合潜艇扰动形成的机理以及控制系统的架构进行深入的分析。

本文所研究的潜载激光武器随动系统是粗、精复合轴模式。粗通道主要是通过直流力矩电机带动的方位和俯仰转台，具有负载大、转动范围广的特点；精通道是在光路中添加快速反射镜(FSM)，FSM是一种工作于光源与接收器之间用于调整和稳定光路的重要装置，一般由两组对称的压电陶瓷堆叠一推一拉实现对负载反射镜方位和俯仰角度的精确控制。由于FSM转动惯量小、精度高(重复定位精度一般<10 μrad)、响应频率高(带宽能达到200～500 Hz)，可以做出更高、更快的响应，从而能显著提高跟瞄系统的带宽与精度，增强其抗扰动能力和稳定跟踪能力。Deng等[9]提出了一种基于扰动观测器的插件模块加速反馈控制策略、针对基于电荷耦合器件(CCD)的FSM稳定系统。Csencsics等[10]介绍了一种适用于Lissajous轨迹电磁驱动FSM系统的控制器。潜载激光武器复合轴跟瞄系统的工作原理如图2所示。由图2(a)可见，光电桅杆搭载于潜艇艇身的围壳之上，图2(b)即为桅杆顶端的放大示意图，内部搭载图3所示的复合轴实验转台。激光经光学透镜射入光电桅杆，再经方位与俯仰转台及FSM调整后射出。

图2 潜艇及潜载光电桅杆示意图Fig.2 Schematic diagram of submarine and electro-optic mast

图3所示为搭载FSM的复合轴实验转台系统，该系统主要由粗通道(力矩电机驱动的方位转台、俯仰转台)、精通道FSM、45°反射镜镜片的楔形体以及CCD摄像头等构成。实验时激光由左侧平台上搭载的激光头发出，经由FSM搭载的镜片反射后由俯仰轴心的圆孔射入，再经45°楔形体反射镜反射出去。

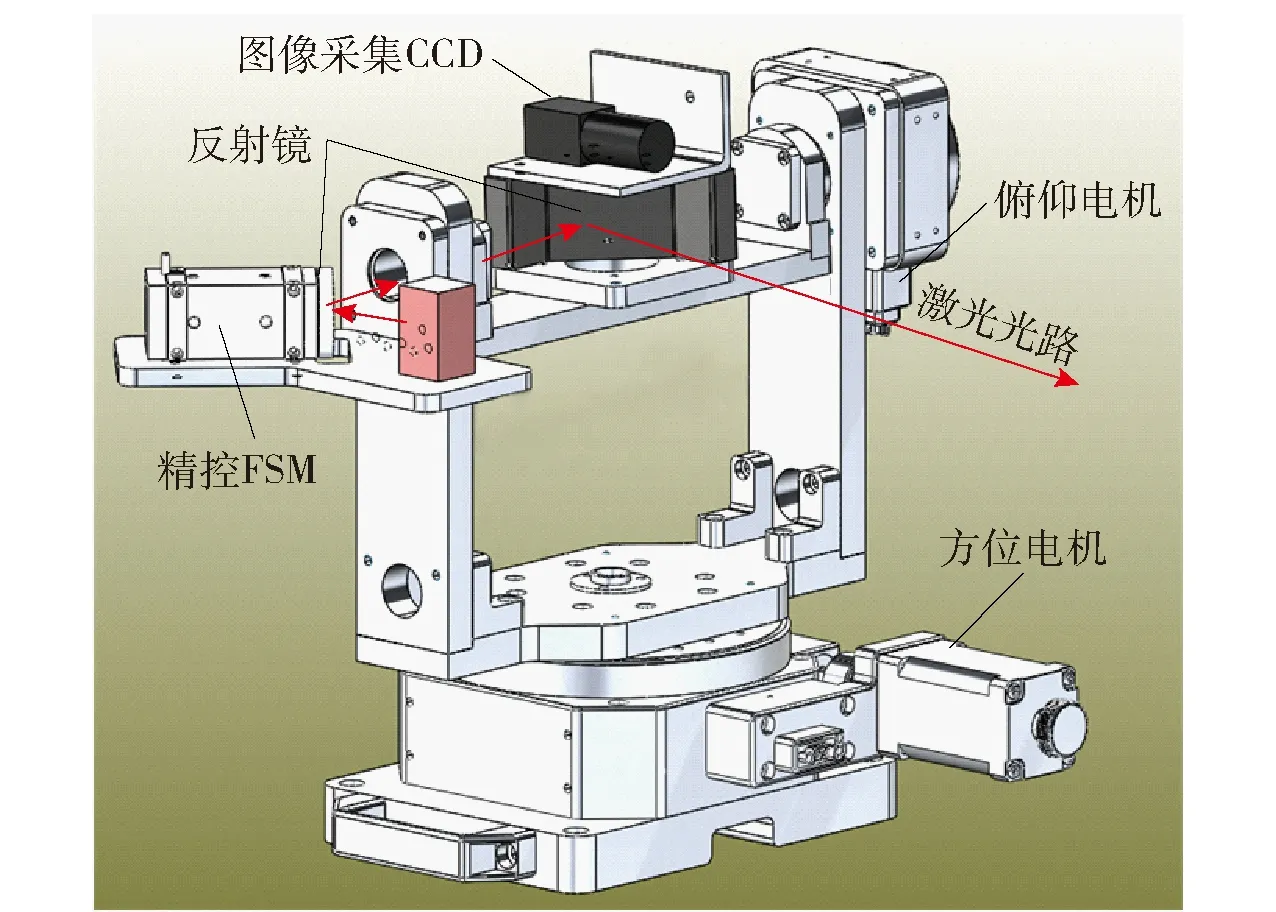
图3 搭载FSM的复合轴实验转台Fig.3 Compound axis laboratory equipment with FSM

为了复现潜艇潜行中的受力和振动噪声，本文首先数值分析了雷诺数Re=1×107条件下6°偏航角的潜艇绕流流场形态与流体动力学特征，将潜艇受到的力矩扰动通过坐标变换解算到随动系统视轴坐标系下，并以此为随动控制系统分析时的光轴方位和俯仰角输入误差；其次对系统执行机构——粗通道力矩电机、精通道FSM进行建模，通过数学仿真软件MATLAB/Simulink工具箱配合适合的闭环控制器对潜艇扰动补偿效果进行了仿真分析，并依托流场演化进一步揭示影响潜艇振动以及跟瞄精度的因素和内在机理。

1 基本模型与数值方法

1.1 基本模型

图4所示为计算用的类潜艇模型，该潜艇主要由半球型头、圆柱型艇身和类圆锥体艇尾组成，其长度分别为0.06l、0.69l和0.25l(l为潜艇的长度，即特征长度)，半球和圆柱体半径为0.06l.
图4(a)中椭圆形为指挥台围壳俯视图，围壳为高0.06l的椭圆柱，其长、短半轴分别为0.045l和0.02l，并与裸艇体相贯于距前缘0.3l处(以椭圆柱中心轴计算)。由于算法采用流体体积思想逼近物体边界，不能分辨小于网格尺度的物体(如带尖角的部分)，因此将模型前后滞点处修改为圆形截面，圆的半径为0.012 5l，此微小改动对流场的影响可忽略不计。

图4 潜艇计算模型Fig.4 Submarine model for numerical simulation

计算区域大小为4l×2l×2l，来流沿x轴正向，右手坐标系原点位于潜艇首端点，x轴指向下游，y轴指向右舷，z轴垂直向上。潜艇首端点(即坐标原点)位于入口下游0.5l处。左、右面分别为速度入口和压力出口，其余4个侧面为压力边界条件，即压力为固定值、法向速度梯度为0，以消除边界堵塞效应，潜艇表面为无滑移边界条件。

1.2 数值方法

无量纲形式的黏性不可压缩流体控制方程为

(1)

(2)

1.2.1 计算区域的树状结构离散

计算区域空间离散通过将正方形(三维为正方体)的有限体积离散成分层组织的四叉树(二维)或八叉树(三维)结构[11-12]。Navier-Stokes方程组的原始变量(U和p)定义在单元中心，表示与该单元对应的体积平均值。以二维四叉树离散为例，定义每个有限体积为单元，每个单元是4个子单元的父单元。根单元是树结构的基础，叶单元是最末端没有子单元的单元。单元的层定义如下：从根单元即0层开始，层数每增加一层，就增加一组紧挨着的后继子单元。同一层上每个单元的每个方向(二维为4个，三维为6个)都通过单元的某个边或面连接。

1.2.2 自适应网格划分

固壁边界由虚拟单元Ghost-cell浸没边界法构建[13]，该方法在处理笛卡尔网格物理边界时不需要改变网格结构。

1.2.3 时间离散与求解

时间离散采用2阶时间交错离散的分数步投影法[14]。这种投影法依靠速度场的Hodge分解：

(3)

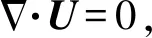
(4)

其边界上的定义为

(5)

由此，无散速度场可以定义为

(6)

(6)式定义了从临时速度场U*到无散速度场U的一个投影算子，其中φ可以通过求解泊松方程(4)式得到。投影算子的离散形式依赖于相应压力场和速度场的离散位置。单元面中心的对流速度采用精确投影法，而在最终单元体中心的速度采用近似投影法。

于是，在给定时间步n，控制方程离散为

(7)

(8)

式中：Δt为时间步长。该方程组用上述时间分裂投影法可以进一步简化为

(9)

(10)

(11)

由(10)式和(11)式可得到泊松方程：

(12)

将(12)式用基于八叉树(三维)的多级求解器求解。离散后的动量方程(9)式可重写为

(13)

1.3 数值验证

为了验证网格无关性、网格层数对计算结果的影响以及结果的正确性，本文结合文献[16]中的实验数据，对SUBOFF型裸艇体绕流流场进行多种层次的网格划分与数值验证。网格划分方法如表1所示，选取背景网格层数为4，对4种不同层数(N=6、N=7、N=8和N=9)固体表面网格和自适应网格进行网格无关性进行验证，网格层数N表示的最小网格尺寸为l/2N.

表1 网格层数的划分与网格总数的估计Tab.1 Division of grid layers and estimation of total grids number

图5所示为不同网格层在计算最终时刻SUBOFF型裸艇体周围的网格分布。由图5可知，随着网格层数的递增，艇体壁面及下游网格越来越密，潜艇头部和尾部曲面能获得更好的拟合，在涡量变化较为剧烈的区域，网格密度显著增加。

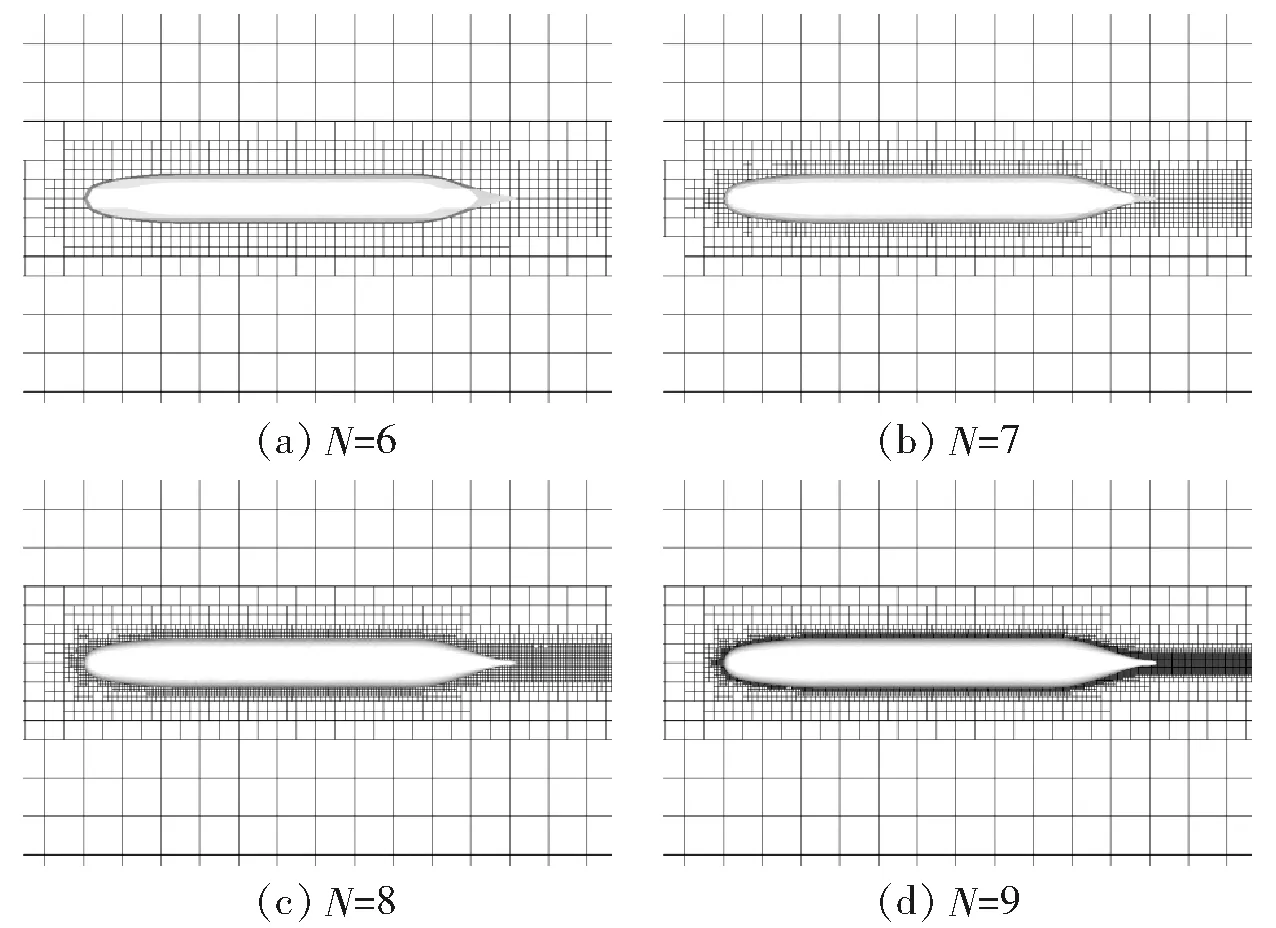
图5 不同网格层数下的网格剖面Fig.5 Cross section of grids with different layers

图6所示为计算得到的不同网格层数下艇体中剖面上压力系数分布。由图6并对比文献[17]中的实验数据可知，艇体中剖面在不同网格层数时的压力系数Cp分布与实验结果变化趋势基本一致。当网格层数为6和7时，压力系数在潜艇头部和尾部有较大的波动，这是因为较粗糙的网格不能充分拟合潜艇头部和尾部曲面；当网格层数为8和9时，压力系数波动较小。这一结果表明，随着网格层数的增加，数值计算得到的压力系数与实验结果有更一致的分布特性。为了更好地分析潜艇流场变化细节，结合所采用服务器的配置与运算时间，本文数值计算采用9层网格，最小网格长度为l/29，总网格数约为2 500 000.6°偏航角的选取是为了在不过多增加计算量的前提下，分析潜艇姿态对扰动的影响。

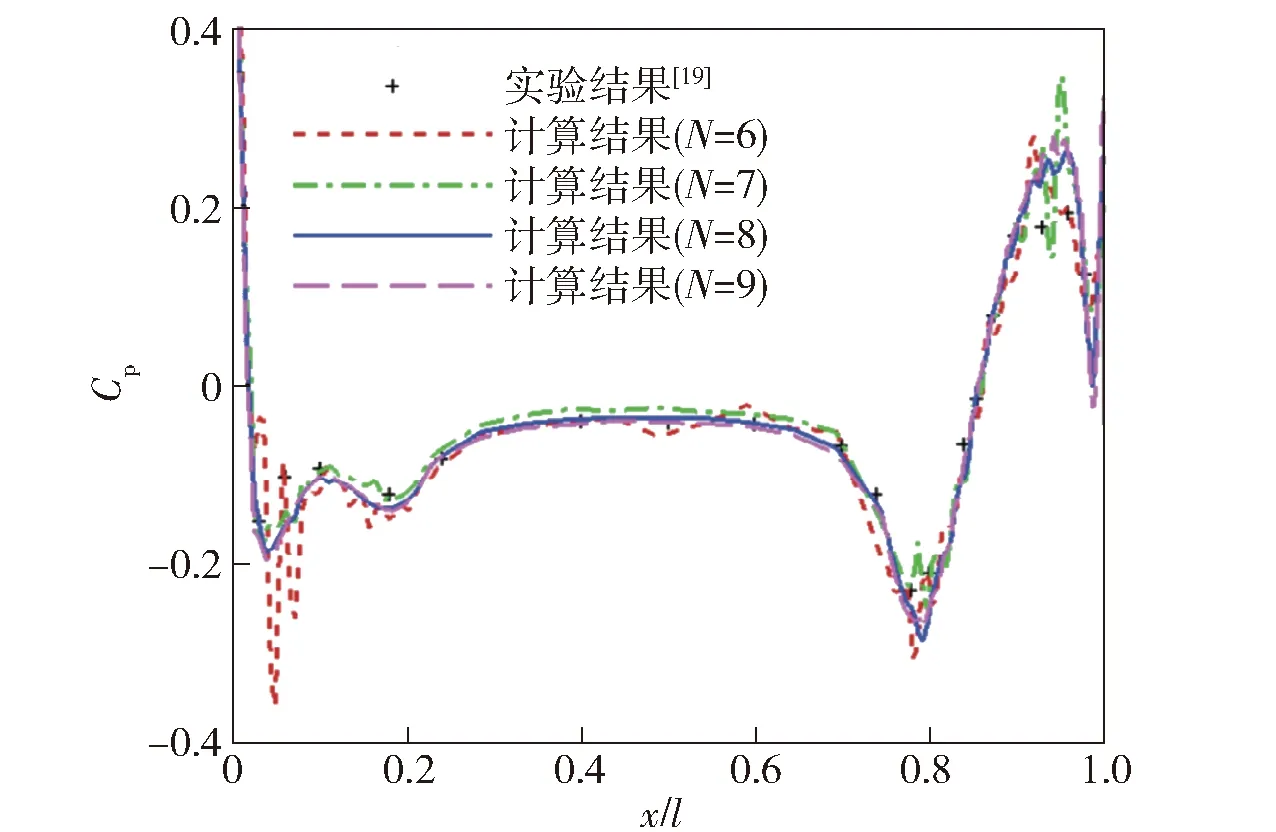
图6 不同网格层数下潜艇中剖面的压力系数分布Fig.6 Pressure coefficient distribution of submarine middle section under the condition of different grid layers

此外，基于这种流场计算方法，刘宗凯等[18]和LIU等[19]对Re=100条件下圆柱绕流进行了计算，并与前人的研究结果进行了对比验证。

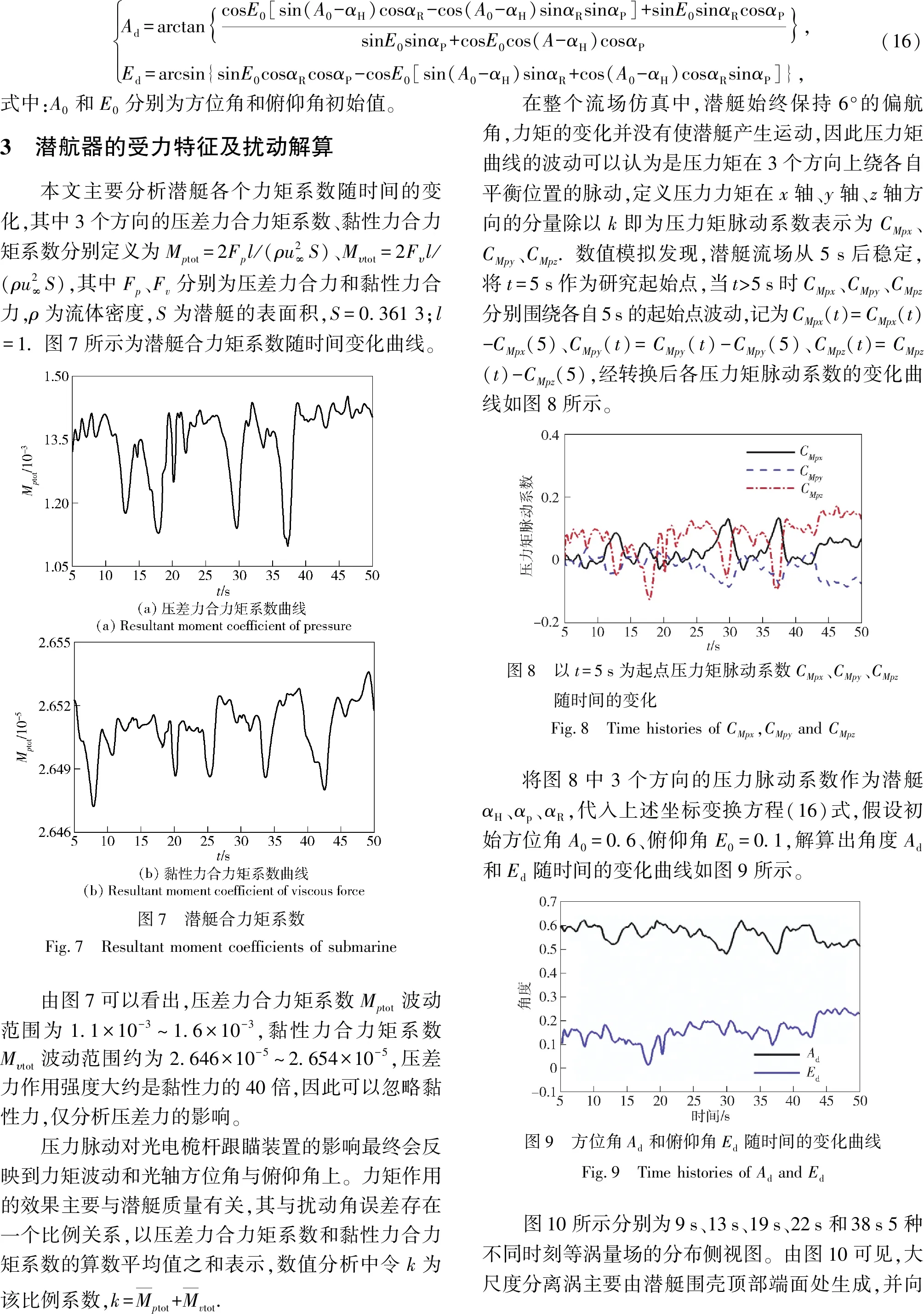
2 光轴方位角和俯仰角的扰动解算

本文侧重于机理研究，只分析潜艇流体动力所产生的扰动，并认为在目标探测器CCD采样周期Δt较低(0.01～0.02 s)情况下，6个自由度的运动并没有超出探测器的视场范围，并将潜艇艇身视为与流体不发生耦合作用的刚性体，即流体压力不会引起潜艇结构的振动。潜艇所受力和力矩变化可以认为与其平移和艇摇运动一致。下面分别对平移和旋转运动进行坐标变换。

视轴扰动角位移模型：潜艇姿态可以用潜艇甲板坐标系与大地坐标系决定的3个姿态角艏摇角αH、纵摇角αp、横摇角αR确定。目标点在大地坐标系中的方位角为A，俯仰角为E. 由于CCD采样时间Δt很小，在单位时间步长内潜艇平移运动引起的方位角和俯仰角变化也很小，相对于艇摇运动可以忽略潜艇平移运动的影响，因此本文仅分析潜艇摇姿(转动力矩)对方位角和俯仰角的影响。

在分别发生艏摇、横摇和纵摇扰动下，目标点在大地坐标系中的坐标(X,Y,Z)可以通过各自的状态转移矩阵TH、Tp、TR经3次摇摆姿势解算得下一时刻的坐标(Xd,Yd,Zd)，合并写成如下矩阵形式：

(14)

将潜艇光轴坐标系下的直角坐标点(Xd,Yd,Zd)转换为方位角和俯仰角 (Ad,Ed)：

(15)

式中：L为斜距，即探测点与目标之间的距离。联立(14)式、(15)式可得