舱室密闭空间中爆炸载荷后燃烧效应数值计算研究

孔祥韶， 徐敬博， 徐维铮， 郑成， 吴卫国

(1.武汉理工大学 高性能船舶技术教育部重点实验室， 湖北 武汉 430063；2.武汉理工大学 交通学院 船舶、海洋与结构工程系， 湖北 武汉 430063)

0 引言

从战例统计和试验资料来看，反舰导弹已成为舰船生命力的主要威胁[1]，舰船在舱内爆炸载荷作用下的毁伤效应分析及防护结构设计成为舰船工程领域研究的热点。准确可靠的舱内爆炸载荷分析对舰船抗爆防护结构设计的毁伤计算起着至关重要的作用。就爆炸冲击波载荷而言，当爆炸发生在舰船舱室内部时，其载荷形式和演化规律与敞开自由空间相比差异较大，约束环境对爆炸作用效果的影响甚为明显。除了初始冲击波之外，爆炸过程中伴随着爆轰产物的燃烧，对后续反射冲击波和准静态压力产生明显的增强效应。梯恩梯(TNT)为典型的负氧型炸药，从其爆炸的总能释放与能量释放率来看，封闭空间内爆炸载荷的能量主要由初始爆炸能和后燃烧效应释放能量组成，其中后燃烧效应释放的能量占总能量的比重近40%[2]，且作用时间尺度为毫秒量级，一般在结构响应的时间范围内。封闭空间内部爆炸的特征主要表现为冲击波效应显著增强、热效应明显、爆轰产物膨胀做功的有效作用时间更长等，除了初始爆炸冲击波的作用外，载荷的燃热增强效应和准静态压力成为重要的毁伤方式。但由于炸药在限制空间内部爆炸的作用过程与目标结构的耦合效应显著，特征参量众多、作用效应复杂，致使有限空间内爆炸特征参量的动态测试、表征及毁伤威力的评估非常困难[3]。

封闭空间内的爆炸载荷研究方面，国内外相继开展了试验及数值计算方面的研究工作。美国劳伦斯利弗莫尔国家实验室Ornellas[4]开展了TNT爆炸产物的燃烧反应对封闭空间内爆炸能量和压力的影响。Ferguson等[5]继承了 Ornellas 在这方面的工作，并进行了更系统深入的研究，采用合并Godunov格式的自适应网格加密(AMR)方法建立了描述TNT 在封闭空间内爆炸后发生燃烧反应的气动模型。Kuhl等开展了TNT 炸药在不同尺寸密闭容器内部爆炸的试验研究[6]，并在试验研究的基础上，开展了相应的数值模拟研究[7-10]，数值模拟与试验结果的对比表明，在引入详细的化学反应动力学过程和湍流混合模型后，数值方法可较好地模拟封闭空间内的炸药爆炸过程，得到了与试验结果吻合较好的载荷历程。此外，Feldgun等[11]、 Donahue等[12]和Fedina等[13]进行爆炸后燃烧效应方面的研究，提出了相应的简化分析模型和数值计算方法。在国内，金朋刚等[14-15]研究了不同气体成分的密闭爆炸罐内TNT后燃烧过程产生的准静态压力，发现在较大氧气浓度下TNT炸药的后燃烧效果较明显，产生更大量值的准静态压力；严家佳等[16]对有限空间中TNT和温压炸药的后燃烧效应进行了对比试验研究；耿振刚等[17]在TNT爆炸试验数据的基础上，应用非线性显式动力学程序ANSYS/AUTODYN计算软件平台建立了坑口爆炸数值计算模型，基于JWL-Miller模型在计算中加入了TNT的后燃烧能量；辛春亮等[18]应用ANSYS/AUTODYN软件平台对考虑后燃烧效应的TNT在无限空域中爆炸进行数值模拟，并将计算结果与经验公式计算值进行比较，采用在爆轰后0.12～0.55 ms内均匀加入燃烧释放能量的方法，发现能量释放率较快导致计算结果出现偏差；李鸿宾等[19]、钟巍等[20-21]开展的试验、理论分析和数值计算结果也证明了爆炸产物的燃烧反应对约束爆炸准静态压力有重要影响。

目前国内外的相关研究工作主要聚焦于爆轰产物的燃烧机理和燃烧释放能量对爆炸载荷的影响规律分析，尚未针对封闭空间内爆炸的作用过程与目标结构的耦合效应提出适用于结构响应计算的封闭空间爆炸载荷评估方法。本文基于ANSYS/AUTODYN软件平台开展了封闭空间内TNT爆炸过程的数值模拟，在考虑爆炸过程与目标耦合的基础上提出了一种简化的计及后燃烧增强效应的舱内爆炸载荷计算方法，并将计算结果与已有的试验结果进行了对比分析。

1 TNT的后燃烧效应

1.1 爆轰能量释放

TNT是一种常用的含能物质，其分子式为C6H2CH3(NO2)3，在爆轰过程中会产生大量高温、高压的爆轰产物，并释放出大量能量。Ornellas[4]通过试验发现，TNT的爆轰能量在4.409～4.573 MJ/kg范围内变化。Donahue等[12]应用Cheetah平衡分析模块计算TNT爆轰的简化平衡方程为

C7H5N3O6(s)→2.2CO(g)+1.6H2O(g)+ 1.5N2(g)+1.1CO2(g)+0.36H2(g)+ 0.2CH4(g)+3.43C(s)，

(1)

式中：下标g、s分别表示物质状态为气态和固态。

根据(1)式计算得到爆轰的能量为4.47 MJ/kg，应用Cheetah完全平衡分析计算得到TNT的爆轰能量为4.495 MJ/kg.

1.2 后燃烧能量释放

TNT的爆轰产物主要是碳、氢气、一氧化碳和甲烷等可燃性物质，在一定的条件下能够继续燃烧，释放出更多能量。在密闭空间中，后燃烧现象的发生需要3个必要条件：存在充足的氧气；爆轰产物与氧气充分混合；气温高于爆轰产物的燃点。当满足这3个条件时，后燃烧现象就会发生。文献[22]经过计算得到在理想的条件下，每千克TNT能量完全释放需要3.17 kg空气，爆轰产物充分燃烧释放的能量为10.01 MJ/kg.

1.3 准静态压力

准静态压力是反映炸药爆轰和后燃烧过程能量释放特性的重要表征参量[3]。本文根据准静态压力确定爆轰产物是否完全燃烧释放能量，从而得到爆炸过程产生的总能量。为了估算炸药爆炸后密闭空间内的准静态压力，Feldgun等[11]基于能量守恒定律提出一种计算准静态压力的简化计算方法，如(2)式：

(2)

式中：p0为标准大气压，p0=101.332 kPa；ρE、VE分别为炸药的密度和体积；ρ0为空气的初始密度；γ0为空气的绝热指数；γ为爆轰产物与空气混合物的绝热指数；Q为单位质量炸药释放的能量；ρ为混合气体的密度；V为密闭空间的容积；p为准静态压力。(2)式中左边第1项为密闭空间中空气的内能，第2项为装药的内能，等式右边为爆炸后系统内的总能量。

为估算炸药爆炸后密闭空间中的准静态压力，(2)式可改写为

(3)

令装药质量W=ρEVE，(3)式可改写为

(4)

(4)式将容器中的气压p表示为装药质量W与容器容积V之比W/V的函数。为了考虑后燃烧效应的影响，对于不同的W/V，要使用不同的Q值。本文1.2节中提到，在理想条件下，1 kg TNT后燃烧反应完全需要3.17 kg空气，空气密度为1.225 kg/m3，因而1 kg TNT的爆轰产物燃烧反应完全需要的空气体积为2.58 m3，后燃烧完全反应与部分反应的临界W/V值为0.387 kg/m3. 当W/V<0.387 kg/m3时，认为后燃烧反应完全，Q取爆轰过程释放的能量与后燃烧反应释放的能量之和，即Q=15.505 MJ/kg；当W/V>0.387 kg/m3时，Q取爆轰过程释放的能量，即Q=4.495 MJ/kg. 还应注意的是，对不同的W/V，绝热系数γ也应取不同的值。根据文献[23]，当W/V<0.387 kg/m3时，γ取为1.40；当W/V>0.387 kg/m3时，γ取为1.25.

将以上条件代入(4)式，得到p与W/V的关系曲线，如图1所示。竖直虚线为W/V=0.387 kg/m3，是氧气是否充足的分界线，虚线左侧表示氧气充足，虚线右侧表示氧气不足。

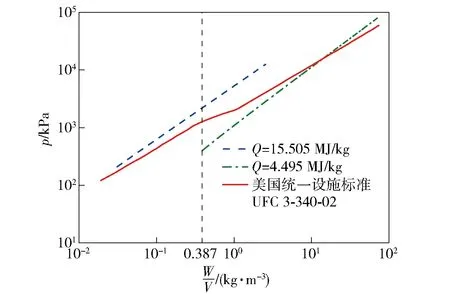
图1 准静态压力与W/V关系图Fig.1 Relation between quasi-static pressure and W/V

2 TNT后燃烧效应的数值计算

为了提供适用于结构响应分析的封闭空间爆炸载荷数值计算方法，本节以加拿大萨菲尔德国防研究和发展部开展的TNT在密闭容器中的爆炸试验为对象[24]，基于ANSYS/AUTODYN软件平台对试验中的TNT爆炸过程进行数值模拟，探索一种简化的考虑后燃烧效应的舱内爆炸载荷计算方法。

2.1 试验装置

图2 试验装置及测点位置[24]Fig.2 Explosion chamber and gauge location[24]

如图2所示，试验装置容积为26 m3，内径3 m，长4.2 m. 容器内壁上P1、P2、P3、P5和P9共5个测点处安装有压力传感器，其中P1、P2、P3在容器侧壁，位于水平中面以上0.254 m的位置，间隔为0.762 m，P5在容器底部，P9位于水平中面以下0.254 m的位置。试验采用的TNT药量分别为3.903 kg和2.100 kg，柱形装药的高径比为1，密度为1 590 kg/m3，使用RP83雷管在装药顶部引爆。

2.2 数值计算模型

根据试验装置的详细尺寸数据，本文基于AUTODYN-3D平台建立了数值计算模型，包括密闭容器结构和空气域，如图3所示。密闭容器结构离散为实体模型，划分为52 660个六面体单元，网格大小为30 mm×30 mm×30 mm. 考虑到试验装置及TNT柱形装药的几何对称性和起爆点位置的不对称性，本文建立1/2计算模型。空气域需将容器完全包含在内，空气域Euler网格尺寸小于Lagrange网格，尺寸为20 mm×20 mm×20 mm.
图4为与试验对应的压力测点布置图，同时为了监测爆炸过程中容器内部的温度变化情况，在数值计算模型中设置了温度观测点，如图5所示。为了提高计算效率，首先在二维空气域中进行装药的爆炸计算，计算到0.4 ms时输出二维计算结果，将二维结果映射到三维计算模型中。

图3 容器和空气域模型Fig.3 Model of chamber and air

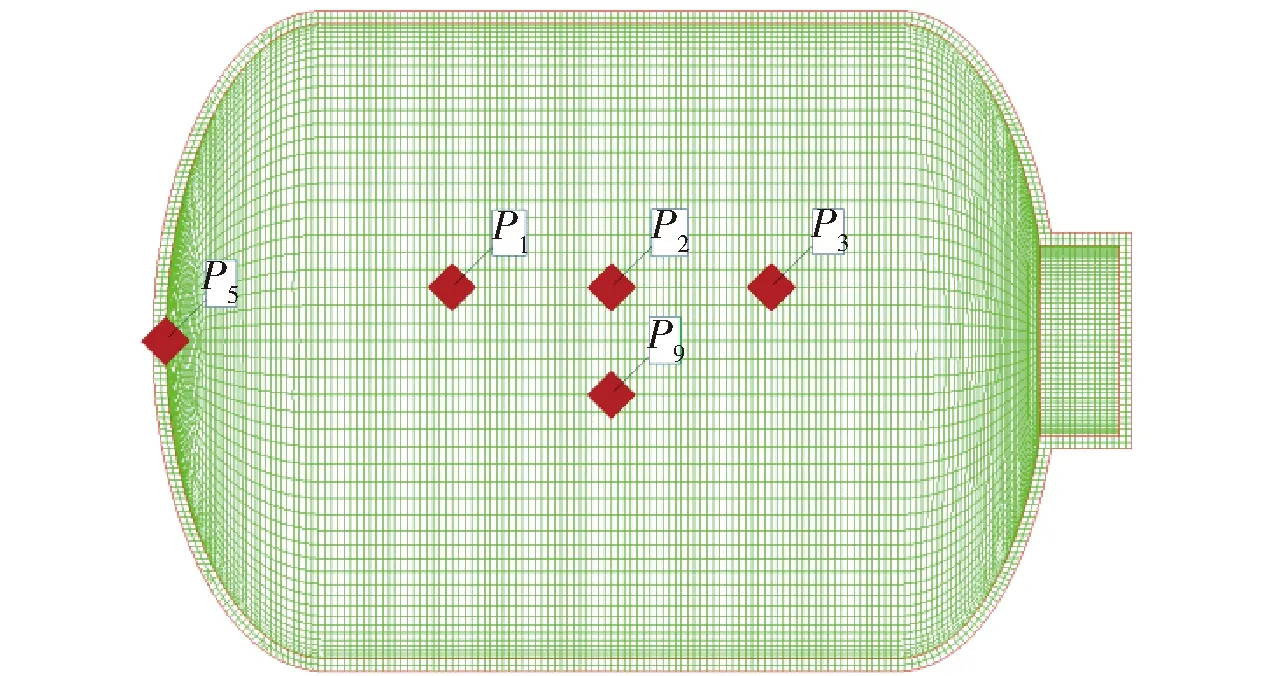
图4 压力测点布置图Fig.4 Arrangement of pressure gauge

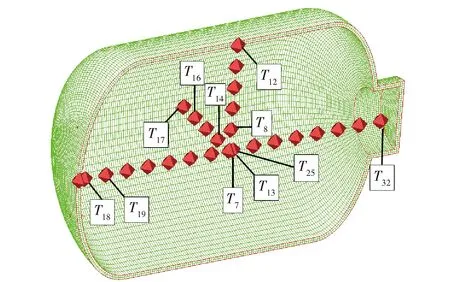
图5 温度测点布置图Fig.5 Arrangement of temperature gauges

2.3 材料模型

数值计算中将密封容器的材料定义为刚体材料，在受到内部爆炸过程中不发生变形。空气域采用理想气体描述，其形式为

p=ρ(γ-1)e，

(5)

式中：ρ=1.225 kg/m3；γ=1.4；e为比内能，e=2.068×105J/kg.

TNT的状态方程采用如(6)式所示的JWL方程：

(6)

式中：pD表示爆轰产物的压力；A、B、R1、R2和ω为常数；V′=ρ0/ρD，ρ0为参考密度值，ρD为爆轰产物的密度。TNT的材料参数如表1所示。

表1 TNT材料参数设置Tab.1 JWL parameters for TNT

JWL状态方程描述TNT这种高负氧型炸药有一定的局限性，它未能考虑到爆轰产物的后燃烧效应释放的能量，因此需要进行补充修正，可在JWL状态方程基础上通过添加附加能量的方式来考虑后燃烧效应。在AUTODYN软件中，可以在TNT的材料参数面板的Additional Option(Beta)中选择Additional Energy项进行附加能量的添加。添加附加能量需要定义起始时间tB、结束时间tE和单位质量TNT的附加能量EA.

TNT在自由场爆炸时，产生的载荷为具有单一峰值且正压作用时间极短的初始冲击波，而炸药爆轰产物发生燃烧主要表现为火球的发展，其位于冲击波峰值之后，二者之间存在显著的时差，因而爆轰产物的燃烧对初始冲击波的影响很小。封闭空间内爆炸产物的燃烧过程与壁面的限制效应密切相关，壁面的限制使爆轰产物与内部空气充分混合；此外，从壁面反射的冲击波进一步压缩空气，使得爆炸空间内部的温度维持在爆轰产物的燃点温度以上，从而使燃烧过程持续并释放能量。据此，本文中能量添加的初始时刻tB为冲击波最先到达容器壁面并反射的时刻；tE为容器内温度降到爆轰产物的平均燃点时刻，tE时刻之后后燃烧反应停止。表2列出了TNT主要爆轰产物的燃点，平均燃点温度为900 K.
图6为容器中温度测点T13～T16的温度时程曲线，由此确定后燃烧反应结束时刻t2=12 ms.
图6中T15、T16测点曲线存在振荡现象，这是因为温度测点位置邻近结构耦合边界处，冲击波反射过程增强，导致压力变化剧烈，进而使得压缩气体的温度出现波动。

表2 TNT不同爆轰产物的燃点温度Tab.2 Ignition temperatures of different detonation products

图6 温度时程曲线Fig.6 Temperature-time curves

开敞工况计算时，为了模拟无限域并考虑到计算耗时，在图3所示的空气域四周(对称面除外)设置流出边界条件。该边界条件将对靠近边界处的数据造成一定的影响，产生振荡效应。因此在开敞环境爆炸工况计算中对温度测点位置进行调整，共设置6个测点：T1点～T6点与爆点的距离分别为300 mm、600 mm、900 mm、675 mm、750 mm、825 mm. 各测点的温度时程曲线如图7所示。对比图6和图7，开敞空间中各测点(T1～T6)温度很快降低到900 K以下，在这个较短的时间段内爆轰产物很难与空气中的氧气充分混合，从而使能量通过燃烧充分释放。关于EA的确定，本文所计算工况为3.903 kg TNT在26 m3密闭容器内爆炸，W/V=0.150 kg/m3. 从图1可以看出，在UFC模型中， TNT爆轰产物没有完全进行后燃烧反应，UFC试验中W/V=0.150 kg/m3测得的准静态压力相当于简化方法中W/V=0.1 kg/m3时得到的准静态压力，相当于3.903 kg TNT中仅有2.6 kg TNT的爆轰产物完全进行后燃烧反应，从而确定本文计算中EA=6.67 MJ/kg.

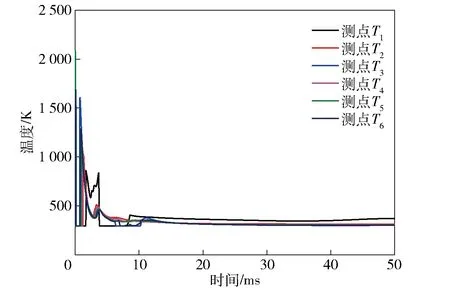
图7 开敞空间中的温度时程曲线Fig.7 Temperature-time curves of explosion product in free field

3 计算结果与分析

准静态压力是表征后燃烧过程能量释放特性的重要参量，为了定量地评估计算结果，本文以准静态压力和冲量作为评估指标，对计算结果进行分析。

准静态压力取测点在20～50 ms时间范围内达到稳定后的平均压力，冲量通过对压力时程曲线进行积分得到。表3和表4分别为仿真计算结果与试验结果准静态压力的对比，对于封闭空间内的爆炸，TNT爆炸产物后燃烧效应导致的准静态压力影响显著。如表3所示，当在计算中不考虑燃烧过程的释放能量时，各测点准静态压力的计算结果与试验的对比误差在55.11%～60.27%之间，50 ms内冲量的计算误差在49.09%～56.38%之间，计算结果显著低估了准静态压力；如表4所示，按照本文提出的简化方法，在计算过程中考虑了TNT爆轰产物燃烧效应后，各测点准静态压力和冲量的计算值与试验值对比误差大大降低，其中P1、P3、P5测点的准静态压力和冲量与试验值比较，误差均在3%以内，P2和P9测点的计算值较试验值略大，准静态压力的对比误差分别为11.55%和8.47%，冲量的对比误差分别为12.51%和10.79%. 由此可见，相对于未考虑燃烧效应的情况，各准静态压力和冲量的计算值更加接近试验测试值。

表3 仿真结果与试验结果的准静态压力对比Tab.3 Comparison of experimental and simulated quasi-static pressures

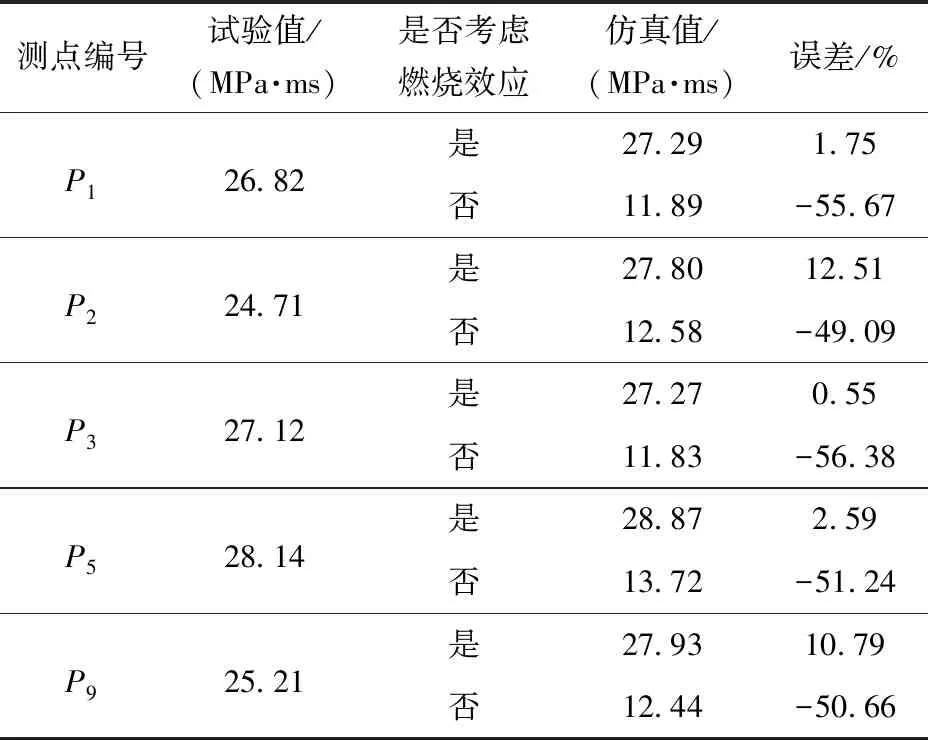
表4 仿真结果与试验结果冲量对比Tab.4 Comparison of experimental and simulated impulses

图8和图9分别为3.9 kg TNT在密闭空间内爆炸时未计及和计及爆炸产物燃烧能量释放效应两种情况下数值仿真计算得到的测点压力和冲量时程曲线。为了便于直观对比，文献[24]中试验记录得到的压力时程曲线也分别绘制在图中。从爆炸载荷压力时程来看，当爆炸发生在封闭空间中时，各压力测点历经的载荷包括初始冲击波、壁面反射冲击波以及持续时间较长的准静态压力，伴随着爆轰产物的后续燃烧能量释放，各测点压力的反射压力在2～6 ms范围内均叠加了显著的压力上升，上升过程随着压力测点位置的不同(测点与爆点的距离不同)而有所区别，但后续的准静态压力值趋于一致。如果数值计算中不考虑爆炸产物的后燃烧效应，则计算得到反射冲击波压力明显小于试验测试值，最终导致准静态压力的计算值与试验值差别较大。从数值计算结果与试验数据的对比来看，考虑了燃烧能量之后，数值计算得到的反射冲击波及准静态压力与试验数据吻合较好，较准确地反映出了TNT在封闭空间内爆炸的载荷特性，可为结构响应计算提供可靠的载荷输入。

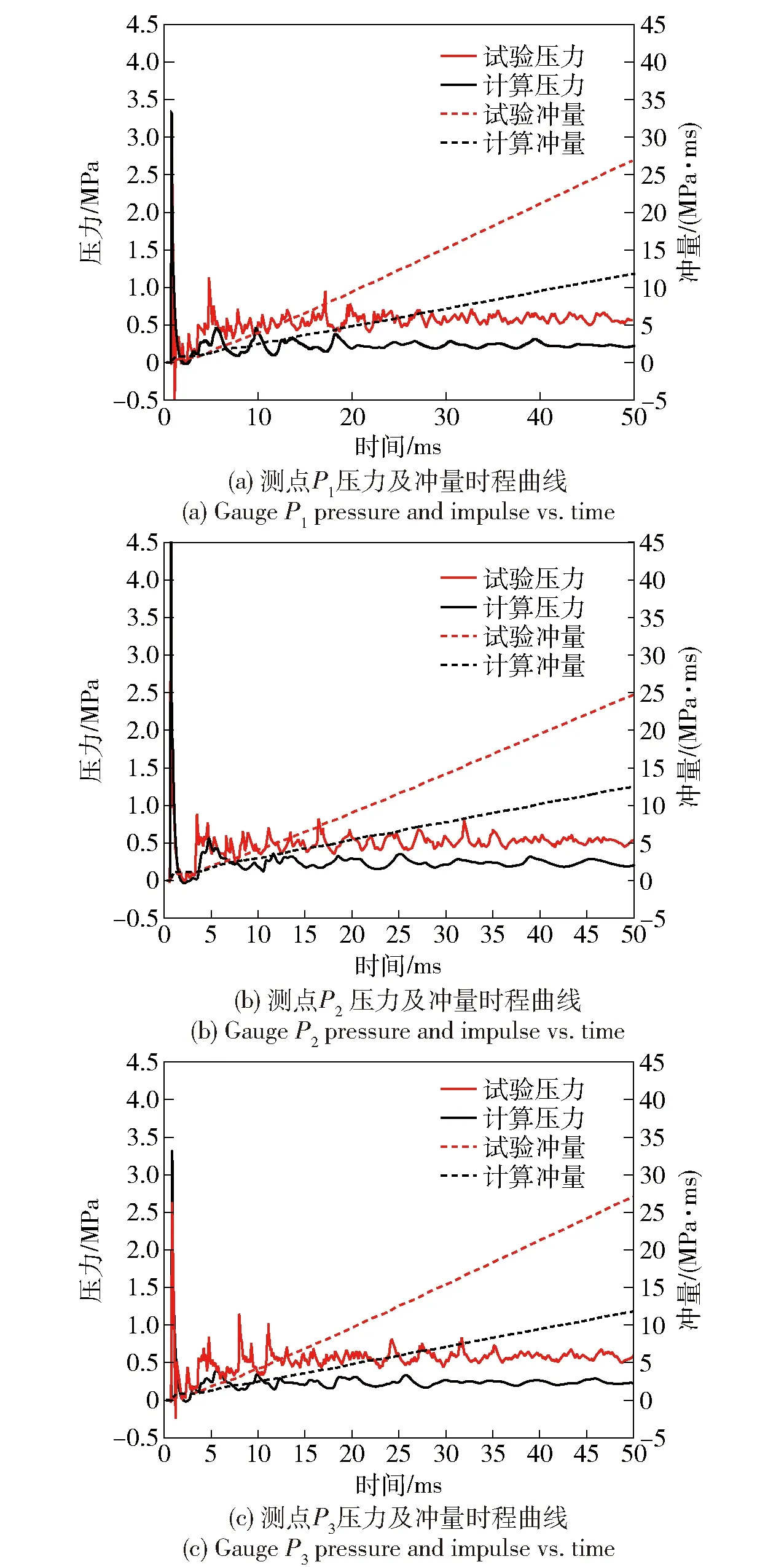
图8 3.903 kg TNT未考虑后燃烧效应的仿真计算与试验测试结果对比Fig.8 Comparison of simulated and experimental results without considering the afterburning effect of 3.903 kg TNT

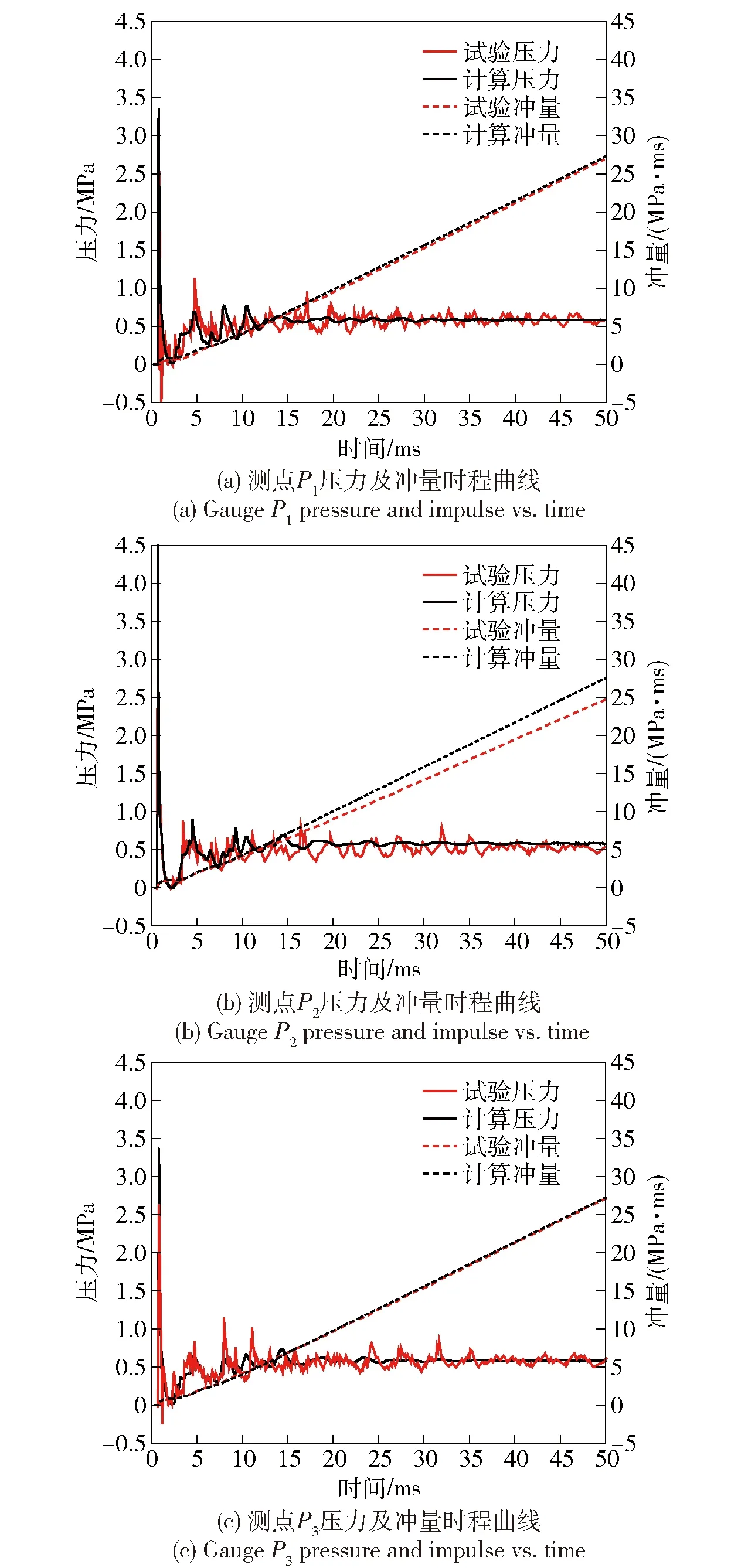
图9 3.903 kg TNT考虑后燃烧效应的仿真计算与试验测试结果对比图Fig.9 Comparison of simulated and experimental results considering the afterburning effect of 3.903 kg TNT

为了进一步验证本文所提封闭舱室爆炸载荷燃烧增强效应的方法，对2.1 kg TNT在图2所示密闭爆炸筒中的爆炸试验进行了数值计算，这种计算工况与3.9 kg TNT的工况相比，二者的W/V值不同，对应的燃烧释放能量也不相同。2.1 kg TNT爆炸工况的计算结果与试验记录数据的对比如图10所示，二者吻合较好。

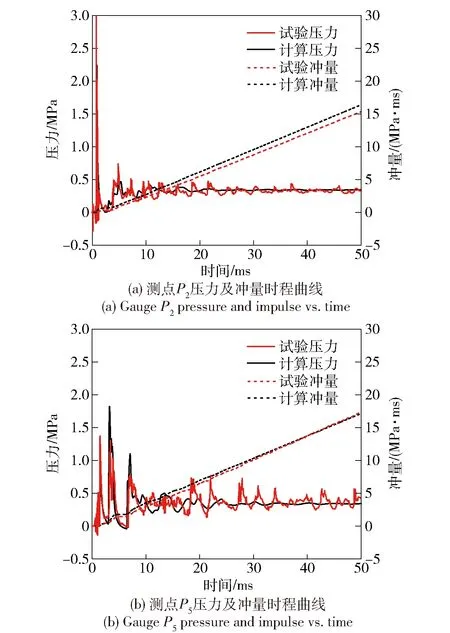
图10 2.1 kg TNT考虑后燃烧效应的仿真计算与试验测试结果对比图Fig.10 Comparison of simulated and experimental results considering the afterburning effect of 2.1 kg TNT

4 结论

本文从TNT爆炸产物的特性分析出发，提出了一种简化的考虑燃烧效应释放能量的计算方法，开展了相应的数值计算，并与试验结果进行了对比验证。得出以下结论：

1)TNT在密闭空间内发生爆炸时，除了爆轰过程释放能量之外，在氧气充足的情况下，其爆轰产物的后燃烧效应不可忽视。不考虑爆炸产物燃烧效应的数值计算得到的准静态压力较试验测试值低55%以上，50 ms内冲量较试验值低49%以上；采用本文方法将爆炸产物燃烧释放的能量计入之后，爆炸压力及冲量时程的计算值与试验值吻合较好，提高了封闭空间内爆炸载荷计算的准确性。

2)本文数值计算中通过在TNT材料JWL状态方程中添加附加能量的方式，将计算得到的燃烧释放能量无差别地添加到每个含有爆炸产物的网格中。这种处理方式在计算内部空间几何形状较简单时适用，但对复杂封闭空间的计算可能会存在误差，需根据实际情况进一步深入分析。

3)由于负氧平衡炸药封闭空间中爆炸时其爆轰产物将发生显著的燃烧，对其他类型炸药在确定TNT等效药量换算时，建议考虑爆轰产物燃烧释放能量而产生的载荷增强，以期为结构抗爆设计和防护能力分析提供可靠的输入载荷。