高性能位置伺服控制系统的Simulink仿真研究

任智博,周 浩

(海军工程大学 兵器工程系,湖北 武汉 430033)

0 引言

高性能数字伺服控制系统是现代工业建设与发展的基础技术。随着数字技术和电气技术的应用与发展,船用伺服系统对数字控制系统的性能有了越来越多的要求。雷达回转机构、武器火控系统的瞄准与击发都离不开高性能位置伺服控制系统的帮助。本文以某船用装备的回转装置为对象进行研究,该回转机构基于数字伺服控制系统技术来实现高性能伺服功能。为了提高传统数字伺服控制系统的动静态性能,实现快速高精度控制,需要在系统中引入诸如自适应控制律、神经网络、微分负反馈控制等先进的控制算法。传统的伺服控制系统普遍采用PID控制策略控制伺服电机,这种方法可靠性好、结构较简单,易于实现,但该方法仍存在响应速度慢、轻载或空载时超调量较大、动态跟踪有滞后的弊端。所以,对于高性能伺服控制,PID控制的优化是十分必要的。文献[1]提出在速度环和电流环上引入前馈控制环节,该方法可使系统正弦信号的跟踪性提高,显著减小系统误差,并且明显缩短系统启动时间,但会引起超调量大的问题。对于连续性的给定信号,该方法效果明显,但对于非连续信号,其改进作用并不显著。为了提高系统性能,必须对系统中的超调量进行抑制[2]。在系统中引入微分负反馈控制算法,该方法可显著减小非连续信号中的超调量,起到快速响应的作用,但对于连续信号的跟踪性的作用不及前馈控制[3]。

在本文中,我们以前馈PID位置伺服控制系统为对象进行研究, 引入微分负反馈环节,以实现快速无差无超调响应,仿真结果验证了本方法的有效性。

1 数字伺服控制系统

1.1 前馈-微分负反馈位置伺服系统结构

数字伺服控制系统由PI电流环、PI速度环、P位置环组成[4],其结构如图1所示。其中,电流环的作用是抑止系统内部的干扰信号与保证电流跟踪性能;速度环的作用是使系统出现扰动或突变时维持速度原有状态;位置环的作用为保证位置实时准确,使系统拥有较好的动静态性能[5]。微分负反馈环节起的作用是把实际位置信号经过微分后加在原值上对其进行修正[6]。前馈补偿的作用是用前馈信号对速度环和电流环的信号进行补偿,具体来说,就是把位置信号微分后产生的速度补偿信号加在速度参考值上进行补偿,对上面的速度环补偿信号再次微分产生的电流补偿信号与电流参考值进行补偿。首先用光电编码器获得实时位置和速度,位置参考值与其反馈信号一起通过比例调节器产生速度参考值,速度参考值与前馈补偿值合并为速度信号,速度信号与实际值通过比例-积分环节产生电流参考值与其前馈补偿值合并为电流信号。在定子绕组中,实际电流值经Clarke和Park变换得到励磁电流和转矩电流,转矩电流参考值与实际值经比例积分环节后得到Q轴电压值,励磁电流值参考值与实际值经比例积分环节得到D轴电压值[7]。把得到的电压值经Park逆变换求得静止两相坐标系电压值。再由SVPWM电路生成PWM波经三相逆变器驱动PMSM。

图1 前馈-微分负反馈伺服位置控制模型Fig.1 Feedforward-differential negative feedback servo position control model

1.2 前馈-微分负反馈位置伺服系统设计

图2 前馈-微分负反馈位置伺服系统控制框图Fig.2 Control block diagram of feedforward-differential negative feedback position servo system

微分负反馈环节和前馈环节同时工作时,输出信号为阶跃信号,经过前馈速度环节一次微分和前馈电流环节二次微分后,得到相关的脉冲函数,其过程对分析微分负反馈环节无太大影响,所以在推导微分负反馈环节时可不考虑前馈过程,系统控制框图如图2所示[8]。

此时系统的闭环传递函数如式(1)所示。

前馈速度环节和电流环节函数如式(2)-(3)所示。

微分负反馈环节与前馈环节同时作用时,电流前馈函数不发生变化而速度前馈环节系数要进行修正,变为

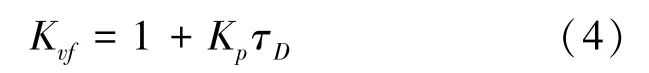
所以系统前馈环节函数变为式(5)。

PMSM单机转矩方程及转矩系数为

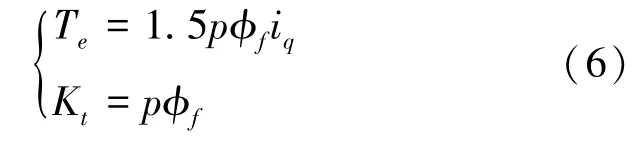
这里我们取电流环增益系数Kc为1,速度前馈系数和电流前馈系数为

2 伺服系统仿真实验

2.1 Simulink仿真模型建立

在MATLAB/Simulink软件中进行仿真模拟实验,建立传统PID控制模型、前馈补偿位置伺服系统模型、微分负反馈伺服系统模型和前馈-负反馈伺服系统模型,为了直观地体现其与原有结构的差异与优势,把他们与原有模型仿真结果在示波器中进行分析比对验证算法的有效性。

我们选用MATLAB/Simulink中已有的PMSM模型为模板进行研究,模型主要由前馈模块、微分负反馈模块、Park变换模块、Svpwm模块、整流逆变模块、检测模块、速度电流PI环节等组成,模型图如图3所示。

图3 前馈-微分负反馈位置伺服控制仿真模型Fig.3 Simulation model of feedforward-differential negative feedback position servo control

2.2 仿真结果及分析

本文中总共做了3组比对实验。第1组实验为有前馈伺服系统与无前馈的对比实验。从图4中与给定信号的跟踪性能对比来看,有前馈的系统在达到稳态时,正弦波形基本重合无相角差,可以得出动态跟踪性能显著优于原有系统。但是不得不注意到的是,在启动时的超调量有一定幅度的增大,原有系统的超调量只有10%,但再引入前馈系统后达到了近20%,所以我们下一步的目标就是减小甚至消除这种超调。

图4 前馈位置伺服系统仿真结果对比图Fig.4 Comparison of simulation results of feedforward position servo system

图5 微分-负反馈位置伺服系统仿真结果对比图Fig.5 Comparison of simulation results of differential negative feedback position servo system

第2组对比实验为微分负反馈系统与原有系统对比,从图5中我们可以看到微分负反馈可以消除超调,但是其跟踪性能又会出现一定的滞后,到达稳态的时间更久。所以综合上述实验结果我们进行第3组实验对比把两种方法结合起来实现既定控制系统性能要求。

从图5我们可以看出第三组实验基本验证我们的方法达到了既定的预期,既消除了跟踪的置后性,又改善了系统存在超调的情况。

图6 前馈-微分负反馈位置伺服系统仿真对比图Fig.6 Simulation comparison diagram of feedforward-differential negative feedback position servo system

3 结束语

本文系统优化设计方法是在传统PID位置控制系统的基础上引入前馈控制环节与微分负反馈控制环节。在前馈环节调试时,我们发现单纯在速度环或电流环上加入前馈环节效果并不能达到既定要求,两者同时加前馈环节时能够更好地解决跟踪误差的问题。其次,根据传递函数表达式来推导前馈控制系数,可以缩短实验模型调试过程。在速度和电流前馈环节的基础上加入微分负反馈,使得系统既保留了前馈环节赋予的良好跟踪性能,又改善了其固有的超调问题。因此,我们可以确定该系统基本上达到了优化设计的目的,具有进一步研究和应用的价值。