基于稀疏动态主元分析的故障检测方法

(浙江理工大学 机械与自动控制学院，杭州 310018)

0 引言

现代工业过程正朝着智能化的方向发展，为了保证产品的质量、避免生产安全事故的发生，实时高效的故障检测系统在工业过程中的作用变得越来越重要。主元分析(Principal Component Analysis, PCA) 作为一种简单实用的多元统计过程监控方法，能够有效地剔除冗余信息，只需要正常工况下的历史数据即可建立模型，在工业过程的故障检测和诊断中得了广泛的应用[1-3]。考虑到过程变量本身的时序自相关性，Ku等[4]提出了动态主元分析方法(Dynamic Principal Component Analysis, DPCA)，通过用带有时间滞后特性的变量构造出动态数据矩阵后，利用PCA方法提取相关主元，提高了故障检测的精度。

但是通过PCA方法得到的负荷向量中的元素通常是非零的，不仅不利于特征的解释和提取，计算量也非常大。为了获取稀疏负荷向量，稀疏主元分析方法(Sparse Principal Component Analysis, SPCA) 近年来得到了极大的发展，并在生物学、医学等各个领域得到了广泛的应用[5-6]。Jolliffe[7]提出了SCoTLASS算法来获得稀疏主元。Zou等[8]提出利用LASSO惩罚项来获得稀疏主元。Leng等[9]提出了简单自适应主元分析，用自适应的LASSO惩罚项取代传统的Elastic Net。Kang等[10]进一步的提出了自适应稀疏主元分析(ASPCA)。彭必灿等[11]，刘洋等[12]，Gajjar等[13]采用SPCA实现了工业过程的故障检测及诊断。Gajjar等[13]并提出一种前向选择方法来确定稀疏主元的非零负荷数目。

本文结合DPCA和SPCA两者的特点，提出了一种基于稀疏动态主元分析法(Sparse Dynamic Principal Component Analysis, SDPCA)的故障检测方法。该方法先通过叠加时间滞后变量的方式建立测量数据的动态增广矩阵，然后再通过Lasso约束函数获取增广矩阵的稀疏主元。此外，本文还提出了一种新的稀疏主元非零负荷数目的确定方法，该方法考虑到了稀疏主元之间的关联性，对文献[13]中提出的前向选择法进行了改进，在保证累积贡献率的情况下，进一步提高了稀疏度。最后，通过数值仿真和田纳西伊斯曼过程来验证所提方法的性能，并与PCA、DPCA和SPCA方法进行对比。

1 基于主元分析的故障检测

1.1 主元分析

给定一个具有n个观测值和m个过程变量的数据集X∈Rn×m，对X进行特征值分解，可得：

(1)

式中，Λ∈Rm×m为特征值的对角矩阵，且对角数值沿对角线递减。V∈Rm×m为酉矩阵，其列向量为主元的负荷向量。

选取V的前k列得到一个新的负荷矩阵P∈Rm×k，可得到得分矩阵：

T=XP

(2)

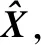
(3)

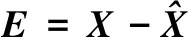
(4)

主元数目的求取可以通过设定贡献度百分比(Cumulative Percent Variance, CPV)来完成，

(5)

式中,CL为设定值，满足上式成立的k的最小值即为满足当前贡献率阈值的最优解。

1.2 主元分析的故障检测

HotellingT2和Q统计量常被用于基于多变量统计法的故障检测。T2统计量由计算主元的得分向量在空间中的马氏距离获得，而Q统计量则是残差向量在残差空间中的欧式距离，

(6)

(7)

式中,xi为数据集在i时刻的m维观测向量，ei为该观测向量的残差向量。

通常，T2统计量的阈值用自由度为k和n-k的F分布计算，Q统计量的阈值则可用χ2分布计算出来：

(8)

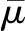
2 基于稀疏动态主元分析的故障检测

2.1 动态主元分析

工业过程一般都具有较强的动态特性，因此过程数据具有强烈的序列相关性。为了解决工业过程的动态特性，DPCA通过扩展观测矩阵，可以消除数据的自相关性，从而提高故障检测的精度[14-15]。

通过在每个观测向量后叠加l个滞后的观测向量来获得增广矩阵，构建方法如下：

(10)

式中是数据集在t时刻的m维观测值，n是总的样本数目。然后将该增广矩阵代替原观测矩阵来进行主元分析。一般情况下，在工业过程控制中序列的滞后参数选择1或2[16]。

DPCA通过增广矩阵可以产生更多的信息关联，比静态PCA更适用于动态工业过程的故障检测。但通过DPCA得到的主元数目过多，使得变量之间的关系更不容易解释，并导致计算量过大。

2.2 基于稀疏动态主元分析的故障检测

本文在DPCA的基础上，提出稀疏动态主元分析法(SDPCA)，通过结合了DPCA和SPCA方法的优点，以提高故障检测的精度，并减少实时计算量，其主要步骤包括：

1)获得动态增广矩阵；

2)确定主元中的非零负荷数目；

3)对增广矩阵进行稀疏主元求解。

首先，通过公式(10)获得设计矩阵，这里参数可采用交叉验证进行选取。然后再确定非零负荷的数目，本文提出了一种新的非零负荷数目的确定方法，并在下一小节中给出具体的过程。最后，在确定的非零负荷数目下，将降维问题转化为回归最优化问题，对其进行稀疏求解。这里，我们采用类似于Zou等[8]提出的SPCA中的优化算法来获取增广矩阵的稀疏主元，即在DPCA模型上增加LASSO惩罚项：

SubjecttoATA=Ik=k.

(11)

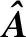
(12)

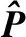
(13)

由于稀疏后的负荷向量不一定是正交的，T2统计量及其控制限的计算如下：

(14)

(15)

其中，γ是稀疏得分向量的协方差矩阵。而Q统计量的计算方式则与PCA模型一致，可采用公式(7)和公式(9)。

2.3 非零负荷数目的确定

如何选择每个主元的非零负荷数目一直是稀疏主元分析的难点。过多的非零负荷会造成计算上的繁琐，所以需要尽可能地减少数目，但同时又要保证剩下的非零负荷拥有足够多的相关信息。

Jolliffe指出当主元的解释方差相近时，约束标准的选择对模型的最终效果影响不大[17]。在此基础上，Gajjar等[13]针对SPCA模型和对应的PCA模型的解释方差之间的联系，提出了一种非零负荷数目的前向选择算法，具体步骤如下：

1)通过公式(1)求解得特征值矩阵。

2)计算可获得稀疏主元的公式(11)，其中主元个数为k，最后一个主元的非零负荷数目为q(k和q的初始值为1) 。

3)如果η1≥90%，则确定q为最后一个负荷向量的非零负荷数目；否则q=q+1，返回步骤2)。

4)当k值与传统PCA(DPCA)的主元个数相同时，或是稀疏后的主元贡献度超过一定阈值时，停止计算。否则k=k+1，q=1，返回步骤2)。

其中，η1为当前SPCA主元的解释方差与所对应特征值的比值，计算公式为：

(16)

但需要注意的是，在 Gajjar等的方法中，每个稀疏主元的非零负荷数目的选择只和它所对应的一个特征值有密切联系，而忽略了与它之前的特征值的关系，可能导致解释方差过低。为此，本文将此方法进行了改进，提出了一种新的基于前向选择的非零负荷数目算法如下：

1)通过公式(1)求解得特征值矩阵。

2)计算可获得稀疏主元的公式(11)，其中主元个数为k，最后一个主元的非零负荷数目为q(k和q的初始值为1) 。

3)如果η1≥80%且η2≥90%，则确定q为最后一个负荷向量的非零负荷数目；否则q=q+1，返回步骤2)。

4)当稀疏后的主元贡献度超过85%时，停止计算。否则k=k+1，q=1，返回步骤2)。

其中，η2为当前k个SPCA(或SDPCA)的方差的和与所对应的k特征值的和的比值，计算公式为：

(17)

在本文提出的算法中，主要依靠来确定非零负荷的数目，因此不仅包含了之前的主元的解释方差信息，也将参数考虑进来，以防止当前的解释方差过低，加强了每个稀疏主元的非零向量数目与特征值之间的联系。此外，还可直接地通过调整贡献度的大小来确定主元的数目。

3 仿真

3.1 数值仿真

为了表明方法的有效性，采用文献[4]的数值例子如下：

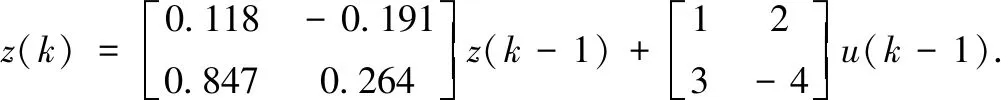
y(k)=z(k)+v(k).

(18)

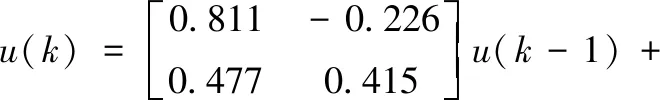
(19)

其中：输入变量w是均值为零，方差为1的白噪声，v是均值为零，方差为0.1的白噪声。输入变量u和输出变量y，均为可测变量。采集正常情况下的100个样本，用于建模。为了模拟故障，在非正常情况下，在第10个样本上引入故障。其中，故障1是，w1变量添加一个单位阶跃。故障2是，将阶跃的幅值增加至3。

为了减少随机变量的影响，本次实验一共生成了1000组数据集。在设置PCA和SPCA的主元个数为3，DPCA和SDPCA的主元个数为4时，DPCA和SDPCA的动态迟滞设置为1。此时PCA和DPCA模型的贡献率可达到98%以上，SPCA的贡献率在92%至96%之间，SDPCA的贡献率在89%至94%之间。4种方法的置信度均设置为99%。表1为分别用PCA、SPCA、DPCA和SDPCA4种方法所得到的故障检测率(Fault Detection Rate, FDR)平均值。

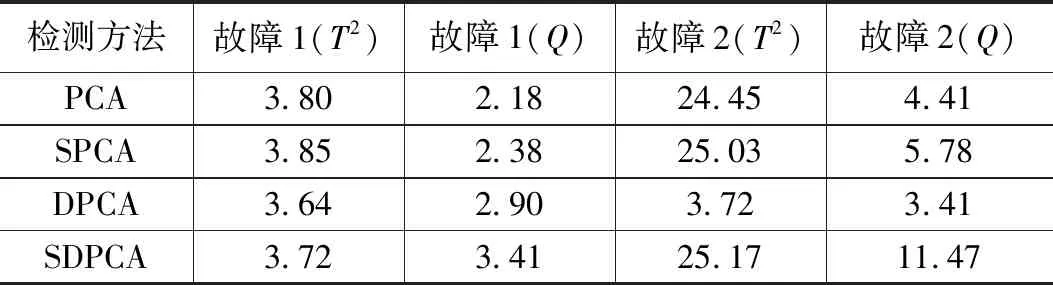
表1 各种故障检测方法的检测率 %

从表1中可以看出，4种故障检测方法在T2统计量下的检测结果差别并不大，但SDPCA方法用Q统计量测得的检测率明显高于其它3种方法。并且从SPCA与PCA、SDPCA与DPCA的对比可以看出，经过稀疏处理之后的检测效果会有小的提升。

3.2 TE过程仿真

田纳西-伊斯曼过程是一种模仿真实化学工业现场的标准控制过程，被广泛的用作控制、优化及故障诊断的仿真对象。该过程主要包括了5个操作单元，分别是反应器、冷凝器、气液分离器、循环压缩机、汽提塔。过程数据的工况被人为设定21种故障情况，每种故障情况以3分钟为采样间隔分别采集了960组采样数据，每组数据含有53个特征变量，每组数据的在第161个采样时刻引入不同的故障。本文选取了第1至22个测量变量及第42至第52个控制变量，共33个特征变量用于故障检测。

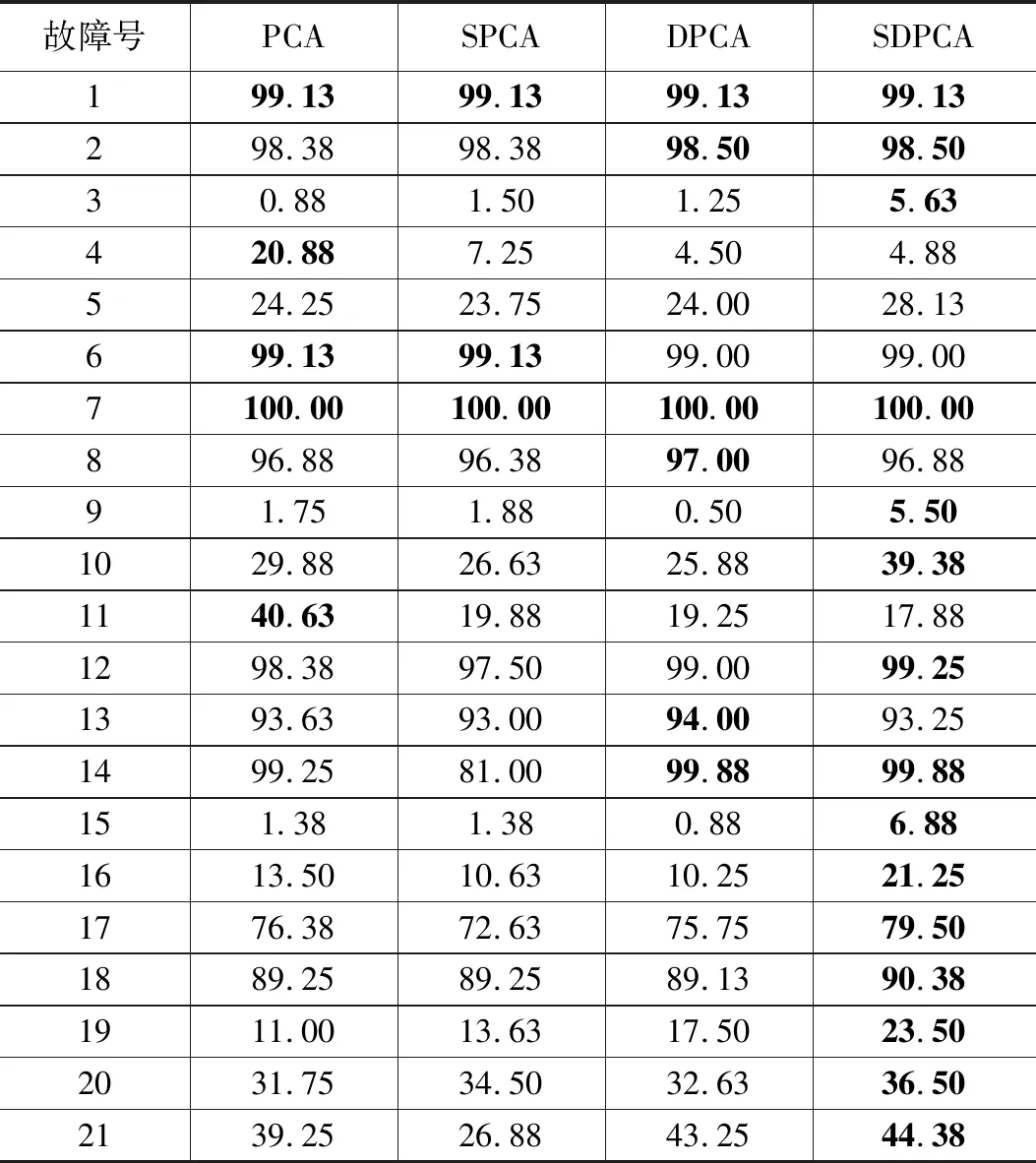
表2 TE过程在T2统计量下的检测率 %

这里，将SDPCA方法的动态迟滞设置为1。经过本文提出的非零负荷数目的选择方法，数据的SDPCA模型一共产生了30个稀疏主元。每个主元的非零负荷的个数分别为24, 23, 9, 4, 5, 4, 2, 2, 2, 2, 4, 2, 2, 3, 2, 2, 2, 1, 1, 2, 1, 1, 1, 2, 1, 4, 2, 2, 2 和 2，贡献率为85.48%。DPCA方法同样选取85%的贡献度，其模型含有24个主元。SPCA与PCA方法的检测数据主元数目均为14。在置信度设为99%情况下，T2统计量检测的结果如表2所示，Q统计量的检测结果如表3所示。表2和表3中，每个故障的最优检测率用加粗字体表示。

通过表2可以看出，4种方法在T2统计检测结果中，SDPCA在其中的16个故障数据下的检测效果都是最优的。特别是故障3、故障9和故障15这几个传统方法难以检测的故障，在其它3种方法下的检测率均低于2%，而通过SDPCA方法在T2统计量下可以得到高于5%的检测率。通过表3可以看出，在Q统计检测结果中，SDPCA方法在11个故障下的检测率都是最高的。尤其在故障10和故障16的检测中，SDPCA在两种统计量下的检测效果均明显优于其它3种方法。图1～4为故障10在4种方法下的Q统计量检测结果。

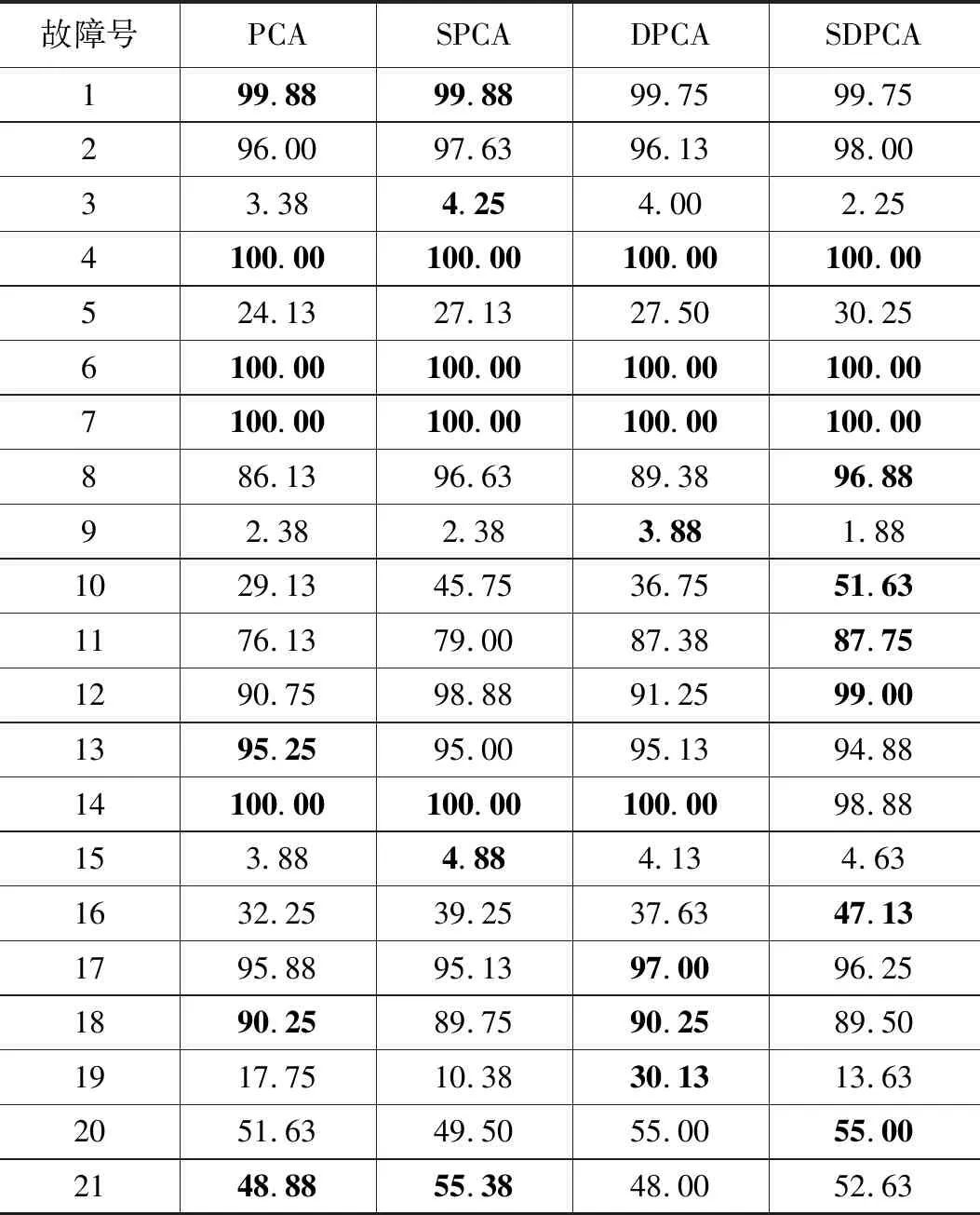
表3 TE过程在Q统计量下的检测率 %

此外，稀疏算法可以有效减少非零负荷的数目， TE过程的数据经过稀疏动态处理之后，SDPCA模型的所有主元中所包含的非零负荷数目为116，而DPCA模型下共包含了792个非零负荷。非零负荷的大量减少，使得SDPCA相比DPCA具有更高的实时计算效率。表4列出了同一台服务器使用MATLAB软件分别用4种方法采用T2统计量处理TE过程故障数据所用的时间。从表中可以看出经过数据动态处理后的SDPCA和DPCA两种方法所花费的时间更长一些，但经过稀疏处理后的SDPCA方法比DPCA方法的检测时间更短一些。

表4 TE过程的检测时间

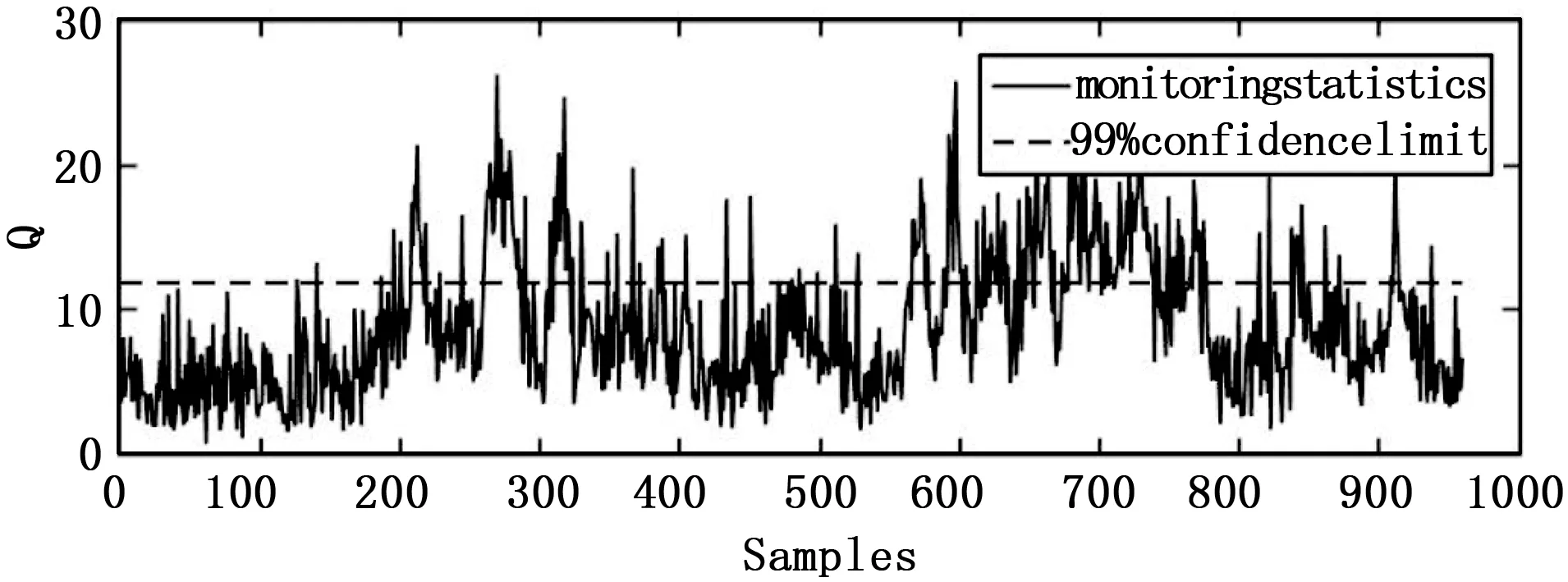
图1 TE过程故障10在PCA下的检测结果

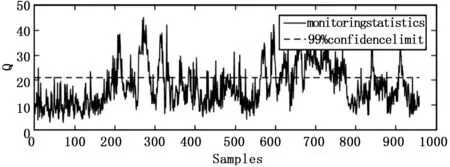
图2 TE过程故障10在DPCA下的检测结果

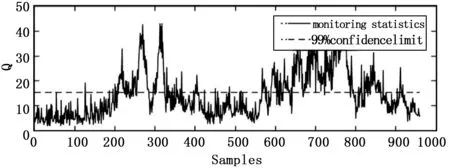
图3 TE过程故障10在SPCA下的检测结果

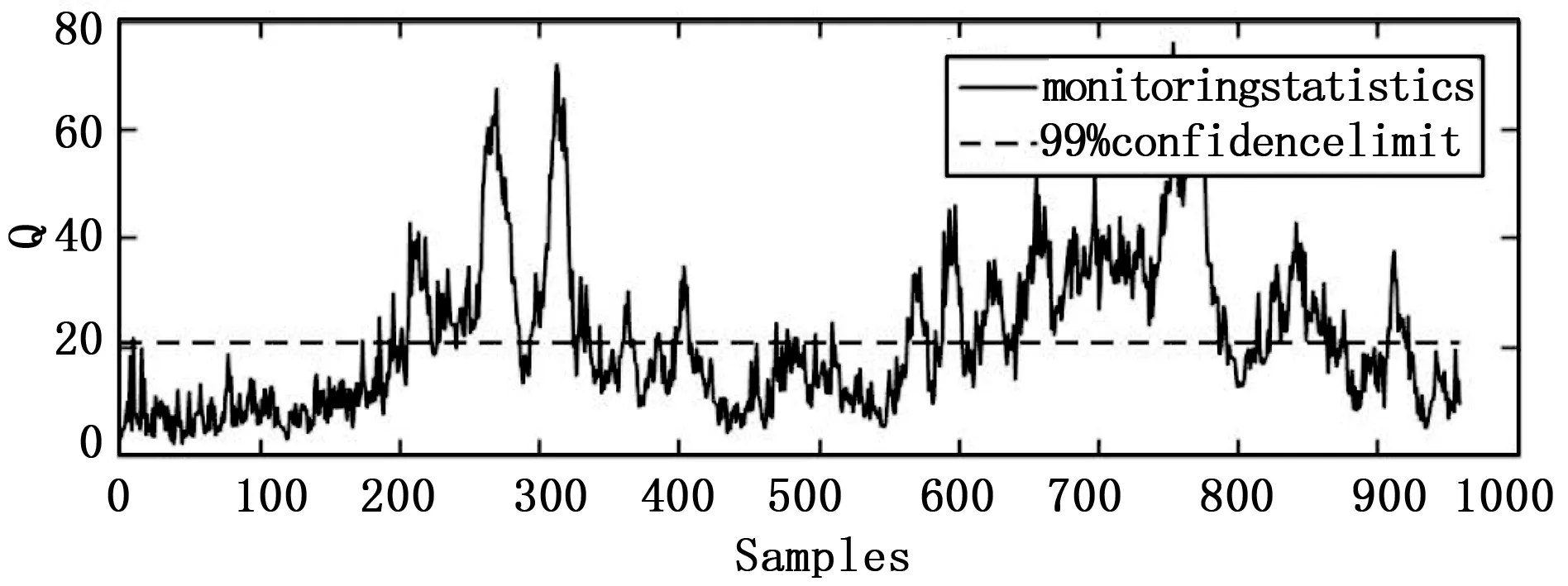
图4 TE过程故障10在SDPCA下的检测结果

4 结束语

结合动态主元分析和稀疏主元分析的特点，本文提出了一种基于稀疏动态主元分析的故障检测方法，并进一步改进了非零负荷数目的前向选择算法。该方法不仅考虑到了实际工业数据的动态特性，同时也大量地减少了非零负荷的数量，从而提高了计算效率，并增加了特征的可解释性。通过数值和TE过程的仿真结果表明，所提方法能够获得良好的动态过程的故障检测性能。未来的研究将进一步研究非零负荷数目的优化选择，以及将动态稀疏方法推广到其它的多变量统计方法中。