分布式电源接入馈线优化规划研究

李文升，宋豪，赵晶，程涛，崔立勃，高国栋，吕宏媛，张媛

（1.国网青岛供电公司，山东 青岛 266002；2.天地电研（北京）科技有限公司，北京 102206）

0 前言

分布式发电DG(distributed generator)是指在用户附近配置较小的发电机组（小于50 MW），以满足特定用户的用电需求或支持现存配电网的经济运行。这些小的机组包括燃料电池、微型燃气轮机、光伏电站、屋顶光伏、风力发电等。分布式电源接入配电网带来提高供电可靠性、利于平衡负荷、提高电网防灾害水平、减小主网投资等一系列积极的影响，同样也会带来电压调整问题、继电保护问题、重合闸成功率、短路电流水平、电网规划设计等一些技术问题。根据国家新能源的战略决策部署，在可预见的未来将会有大量分布式电源接入配电网，传统配电网规划方法无法满足分布式电源接入的规划需求。从规划层面实现分布式电源接入的顶层设计，为规划技术人员及企业管理人员提供决策依据变得非常迫切。

国内对分布式电源的准入容量及最优位置做了大量的研究，文献[1]文中应用遗传算法优化分布式电源的位置和容量，并运用基于支路交换的模拟退火算法规划扩展网络，对分布式电源和网络的综合规划结果进行经济性评估以衡量个体方案的优劣。文献[2]文中基于放射状链式配电网连续解析模型和离散模型，研究多台分布式电源装置接入系统对沿线电压和有功网损的影响，探讨分布式电源的最优接入位置。文献[3-5]应用静态负荷模型，以电压不越限与线路载流量为约束条件，建立了分布式电源准入容量和接入位置分析，以网损最小为目标函数，将准入容量纳为约束条件建立分布式电源最优布置函数。文献[6]从电力系统静态安全约束的角度出发，建立了计算分布式电源准入容量的数学模型。对于多个分布式电源的情况，提出了准入容量计算的双层优化模型和相应的优化求解算法，并通过对实际配电系统进行分析，验证了该方法的正确性和有效性。以上文件提出了基于电网静态约束的较为科学、严谨的计算馈线准入容量的计算方法，但计算过程较为复杂，也尚未提炼出可用于工程实践的一般性的指导原则。

本文从配网实际接线模式出发，研究馈线、变电站最大接入能力；基于成本效益分析，研究馈线最佳分段；以网损最小为约束，研究分段容量与分布式电源接入容量的匹配关系。在理论研究基础上，建立简化计算模型，采用电网典型计算参数，求取计算结果，并进一步总结提取一般性的指导性原则，为规划技术人员提供简单易行的决策依据。

1 馈线的分布式电源最大接入能力

以电压限制为约束计算馈线的分布式电源准入容量，并考虑极限情况，每条馈线均采用最大准入容量接入，以电网的安全可靠性运行准则校验接入是否可行。

以环网连接辐射运行的配电网络为例，分析计算分布式电源接入的容量限制。假设在K点输入有功功率Pdg的分布式电源。

图1 计算模型示意图

1.1 电压限制下的单条中压线路

按电压允许值计算的最大接入能力[3]，分布式电源接入点K的电压为：

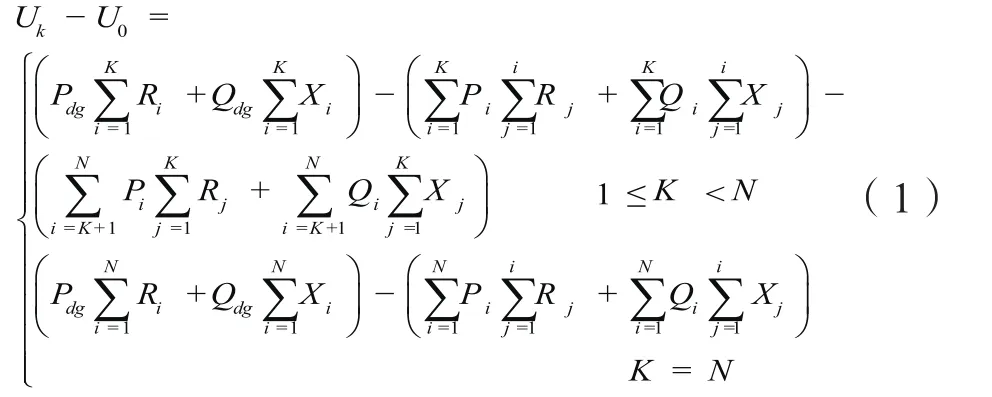
其中，Uk为第k节点电压；U0为母线侧电压；Pdg为分布式电源有功出力；Qdg为分布式电源无功出力；Ri为线路i电阻值；Xi为线路i电抗值。

若分布式电源接入点达到电压极限，分布式电源达到该接入位置处的最大接入能力。根据我国相关规定，10 kV与380V电网节点电压不得超过1.07 p.u.假设功率因数λ恒定，代替Qdg，求解上式Pdg。由于在推算过程中忽略了线路损耗，按上式计算得出的准入容量偏小，因此引入修正系数α，一般可取1.03-1.08，约为网络正常运行时的网损比例。分布式电源准入容量与接入位置之间的函数关系为：

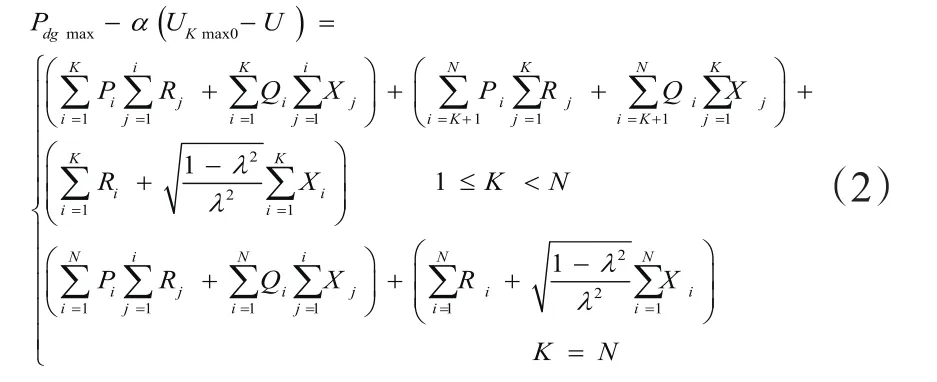
针对常见的配电网负荷分布进行进一步简化。常见的配电网负荷分布包括沿负荷馈线均匀分布、递增分布与递减分布等。这里介绍一下常用的均匀分布情况。

在负荷均匀分布情况下，有Pi=P/N，Qi=Q/N，Ri=R/N，Xi=X/N，代入Pdgmax的求取公式得出：

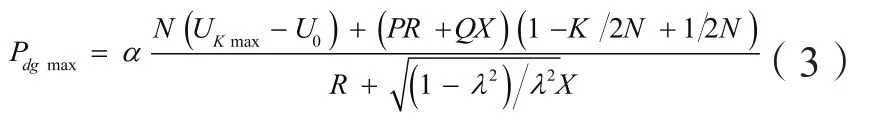
《电能质量 供电电压允许偏差》GB12325－2008，供电电压偏差允许值20 kV及以下三相供电电压偏差为标称电压的+7%，-10%，按电压升高0%至电压升高7%分别计算Pdgmax，从计算结果可以看出，电压升高百分比越大，Pdgmax越大，节点位置离母线越远，Pdgmax越小。

选取架空线路及电缆线路典型型号计算给出单条不同类型中压线路准入容量，可以看出：从电压限制来看，单条线路准入容量可达线路最大输送能力，一般取9 MW。同等容量接入的电缆线路电压偏差较架空线路电压偏差大。

1.2 N-1安全标准下变电站供带馈线

根据DL/T5729-2016[7]，供电安全准则是保障配电网安全可靠供电的重要基础，主要以是否满足N-1校验的方式评估。变电站满足N-1校验，可供带负荷即为该变电站最大安全供电负荷。

从保障配电网安全可靠供电角度，分布式电源接入后配电网应仍要求满足N-1校验。N-1安全标准下的变电站最大接入能力计算思路为：分布式电源出力就地平衡馈线负荷后，多余出力通过变电站上送，变电站应满足N-1校验，即一台主变故障情况下另一台主变不过载且不弃电源出力。

基于以上思路，变电站供电范围内的负荷最小、分布式电源出力最大分情况对应变电站的最大接入能力。计算公式为：

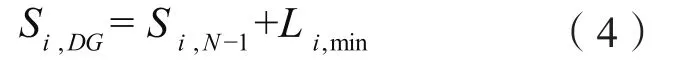
通常，电网规划预测给出地区最大负荷或变电站最大负荷，但不会预测最小负荷。可以基于最大负荷预测值及现状电网最小负荷与最大负荷比例估算变电站最小负荷。计算公式为：

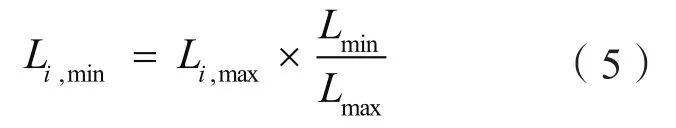
其中，Si,DG为第i座变电站供带馈线最大接入能力；Si,N-1为一台最大容量主变故障情况下变电站剩余总量之和；Li,min为第i座变电站最小供电负荷；Li,min为第i座变电站最大供电负荷；Lmin为地区现状最小供电负荷；Lmax为地区现状最大供电负荷。

2 馈线最优分段研究

不同分段馈线的供电可靠性差异较大，分段的合理与否直接关系到负荷用户及分布式发电商的停电损失。本文结合发电商利益、供电企业投资、社会用户停电损失等各方要素分析给出馈线的最优分段区间。

2.1 最优分段计算模型

分布式电源接入配电网将会提升配电网可靠性，具体表现在电网出现故障且故障隔离后，分布式电源可供带部分负荷，减小停电范围的同时缩减停电时间，进而提升供电可靠性。分段数的增加带来可靠性提升，但也相应增加投资。本文建立架空及电缆系统的成本效益分析模型，采用故障遍历法分析停电影响，绘制成本效益曲线，求解合理分段范围。

图2 典型架空系统分布式电源接入模型示意图

图2 给出典型架空分布式电源接入示意图。本模型以联络接线为例分析，逐一遍历段内线路故障情况下停电、复电过程及相应影响，并汇总形成综合停电结果。由于线路故障率远高于开关故障率，因此忽略开关故障影响，段故障率等效为段内所有线路长度的故障率。以架空线路为例给出逐一遍历过程：假设第i段出现故障，第i段线路两侧开关识别故障自动跳开，实现故障自动隔离，该段用户及发电企业均为修复完成后恢复供电，其余段在主站评估优化孤岛供电范围后恢复分布式电源的供电负荷。

分别评估计算该停电过程中带来的户均停电小时数、用户缺供电量及停电损失、发电商减发电量及减发损失。

2.1.1 户均停电小时数评估

第i段故障，停电时户数可表示为：

其中，Si为第i段故障停电时户数，单位h·户；L为线路总长度，单位：km；n为线路分段数；N为用户数；M为分布式电源数量；SG为分布式电源装机容量，单位：MW；SV为馈线最大输送容量，单位：MW；TREP为故障修复时间，单位：小时；TCE为分布式电源供电范围优化决策时间，单位：小时。

遍历所有分段，计算总停电时户数：

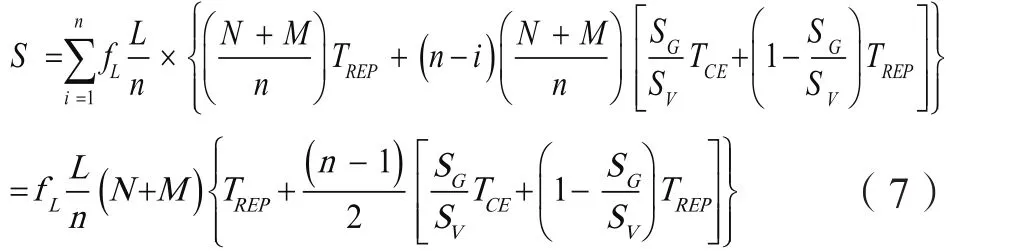
计算户均停电小时数：

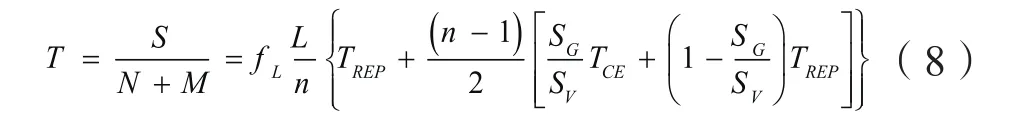
2.1.2 用户缺供电量及停电损失评估

在求得的户均停电小时数基础上，乘以单位电量停电损失，求得用户停电损失。单位电量的停电损失可等效为度电产值，缺供电量计算公式为：

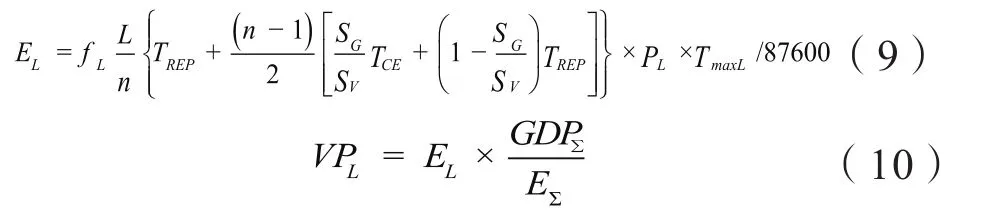
其中，EL为用户缺供电量，单位：万kwh；PL为馈线最大负荷，单位：MW；TmaxL为负荷利用小时数，单位：小时；VPL为用户停电损失，单位：万元；GDPΣ为地区国民生产总值，单位亿元；EΣ为地区总供电量，单位：亿kwh。

2.1.3 发电商减发电量及减发损失评估

电网侧故障造成用户停电的同时，分布式电源孤岛保护脱网，隔离故障后，恢复部分供电。计算发电商停发减发电量及损失，计算公式为：

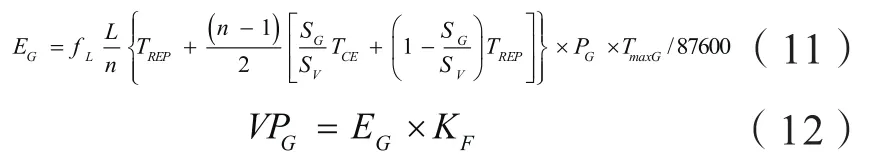
其中，EG为发电商减发电量，单位：万kwh；PG为分布式电源最大出力，单位：MW；TmaxG为分布式电源发电利用小时数，单位：小时；KF为单位电量上网电价，单位：元/kwh。

2.2 典型网络最优分段

选取典型架空系统单联络接线模式，假设线路负荷均匀分布于分段间，馈线实施配电自动化，且为智能分布式配电自动化，开关具备遥控功能。分别计算不同分布式电源机容比情况下的最优分段。计算结果绘制图3所示的曲线。

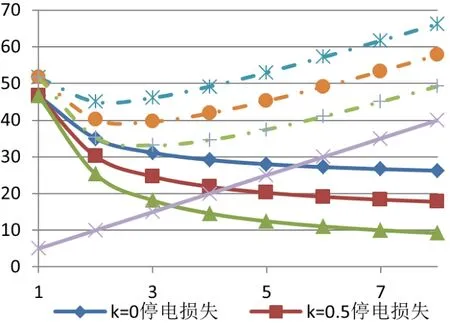
图3 不同机容比情况下的停电损失与投资的关系曲线

可以看出，k值越大停电损失曲线越低越陡，说明分布式电源装机容量越大对供电可靠性贡献越大，若对分布式电源装机容量大的馈线增加分段，相应的停电损失也降低越多。也就是，分布式电源装接容量越大的馈线对分段越敏感，但增加分段也意味着投资增加，总成本相对较小区间3-6段为合理范围。另外，从单位投资降低停电损失效益角度来看，4-6段停电损失曲线斜率平稳（斜率趋于0），6段后再分段作用效果不明显。综合以上，推荐最优分段为4-6段。

2.3 分段装机容量与配变容量匹配关系分析

馈线分段内应该如何配置装机容量与配变容量是馈线规划需要解决的一个问题，如果分布式电源容量装接过多，可供带本段及前后多段的负荷，供电负荷大、供电距离长，网损也大；分布式电源装接容量过小，下网电力增加，远距离送电，网损也变大。本文以网损最小为约束条件，分析段内装接容量与配变容量的最佳匹配关系。

假设负荷沿线均匀分布（如图1），已知分布式电源的容量来求取最优接入位置，求取线路网损Ploss函数对接入点x0的偏导数，即求得在该接入容量下网损最小的最佳接入位置[3]。

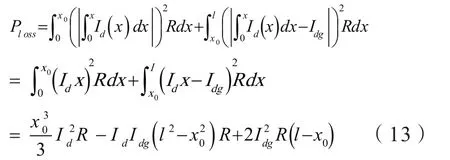
计算网损最小情况下的最优接入位置

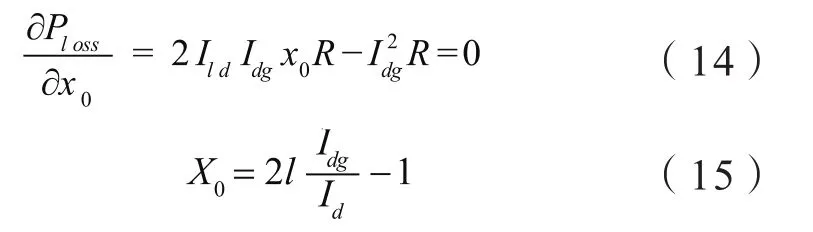
可见，容量为Idg的分布式电源最优接入位置为21Idg/Id。同样，由上述公式计算已知接入点情况下的最优接入容量Idg=(I+x0)/21Id。

假设馈线分为4段，由以上公式计算得出：当在第一个分段处接入分布式电源，最优接入容量为线路最大负荷的7/8；在第2个分段处，分布式电源最优接入容量为最大负荷的3/4；线路末端接入，接入容量为最大负荷的1/2。可以看出，分布式电源供带接入点及下游负荷的同时向上供带至10 kV母线侧一半的负荷，网损最小，也就是分布式电源就近消纳损耗最小。同理，若馈线沿线有多个分布式电源需待接入，段内就近消纳损耗最小。本文提出“段内机容匹配原则”，即分段内分布式电源装接容量与配变装接容量相当。可表示为

式中SG为段内分布式电源装机容量；SV为段内配变装接容量；RL为线路平均负载率；RG为分布式最大概率出力比例。通常情况下RL约为30-40%，约与分布式电源最大概率出力区间相当，该比例系数可取为1。

3 分布式接入馈线规划流程

1）预测区域最大负荷预测值，进行电力电量平衡，规划变电站座数及变电容量；

2）预测变电站最大负荷、最小负荷，计算变电站最大接入能力及馈线最大接入能力；

3）基于地块负荷结果，进行中压馈线及配电设备规划，设置最优分段；

4）根据段内机容配比原则，分段内接入最优分布式电源容量；

5）校验变电站下所有中压馈线分布式电源的加总容量，若超出变电站最大接入能力则削减馈线接入容量直至满足为止。

4 算例

选取某新建经济开发区开展算例应用，开发区面积为11.56平方公里，用地性质以高端产业、科技研发、商务居住为主。该区域分布式电源主要光伏发电，10 kV电网接入。新建开发区A1地块分布式电源分布示意图如图4所示。

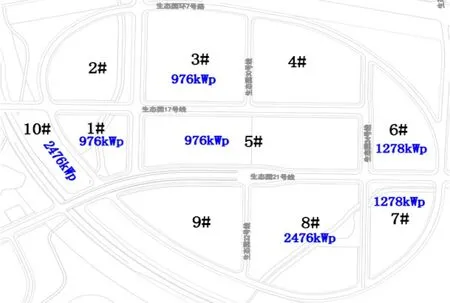
图4 经济开发区A1地块分布式电源分布图

4.1 可接入分布式电源总容量分析

根据负荷预测，开发区2020年负荷预测值为90 MW，规划2座110 kV变电站供电，变电站总容量200 MVA。每座变电站最大负荷为45 MW，全年最小负荷与最大负荷的比例系数为40%，变电站最小负荷为18 MW。变电站最大接入能力为：

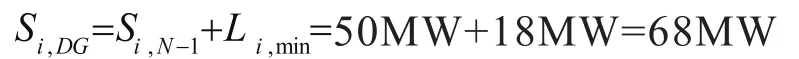
共计可接入136 MW。规划10 kV馈线20条，平均单条馈线接入分布式电源6.8 MWp，最大接入9 MWp。

4.2 分布式电源接入规划

根据分段方式、分布式电源接入方式的不同，提出两种方案：

方案一：馈线分为3分段，分支馈线分布式电源装接容量超过3 000 kWp。1#、3#、5#、10#地块分布式电源集中接入第一分段的分支上。

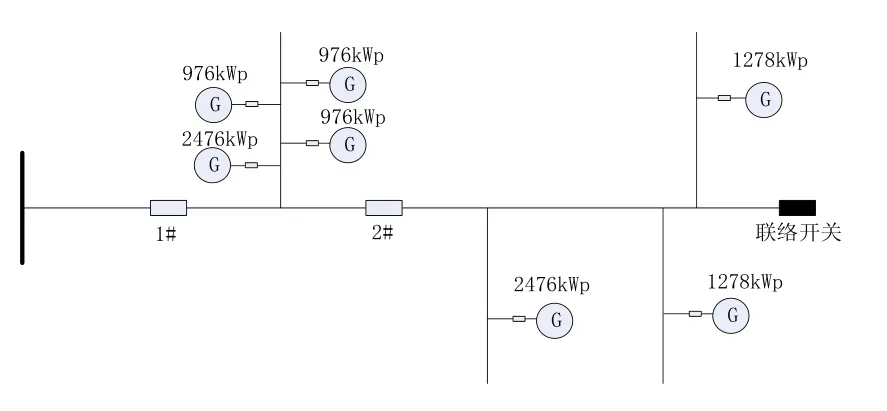
图5 A1地块供电方案1示意图

方案二：馈线分为4分段，分支馈线分布式电源装接容量均小于2 400 kWp，超过者增加分支。每段的接入容量按照本文所提“段内机容匹配原则”。10#地块2 476 kWp接入1#分段，3个976 kWp接入2#分段。平均分段容量为2.5 MVA，平均分布式电源装接容量约为2.4 MWp。

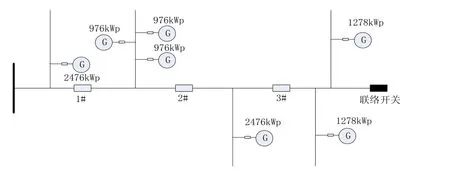
图6 A1地块供电方案2示意图

4.3 规划效果分析

计算方案一与方案二的供电可靠性、网损等相关指标，计算结果见表1。

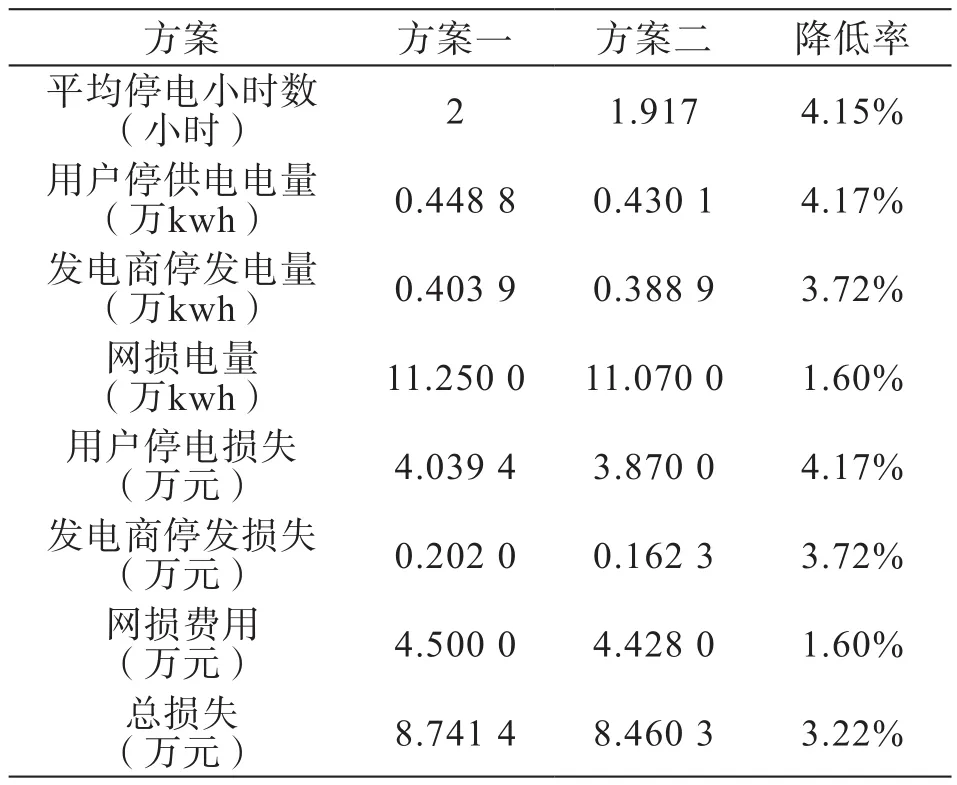
表1 不同规划方案效果计算

可以看出，采用方案二供电可靠性停电损失降低4.17%，发电商停电发电量降低3.72%，网损相对降低较小为1.6%。可以看出，优化分段、采用“段内机容配比原则”接入分布式电源规划对电网各项技术指标均有影响，特别是用户停电损失，因此推荐方案二。

5 结束语

本文基于理论研究基础上，设置电网典型计算参数，总结提出一般性规划原则，具体如下：

1）若考虑配变低压侧配置无功自动投切装置，馈线分布式电源接入容量受限于最大输送容量。变电站接入分布式电源总容量为变电站N-1容量与变电站最小负荷之和。

2）对于分布式电源容量越大的馈线，增加分段对故障停电损失降幅更加明显，但考虑分段投资，最优分段取为4-6段。

3）基于网损最小约束条件，提出“段内机容匹配原则”，即段内配变容量与段内分布式电源装机容量配置相当。

本文所提的方法及一般性原则是面向馈线典型接线模式做出的尝试性研究，当接线模式较为复杂，分布式电源接入容量差异较大的情况，求解将更加复杂，如何采用有效的算法求解有待进一步研究。