内置式永磁同步电机交直轴电感研究
叶小奔 钟成堡,2 陈飞龙 谢 芳 刘 娜 张 闯 杨文德
(1.珠海格力电器股份有限公司 珠海 519070;2.空调设备及系统运行节能国家重点实验室 珠海 519070)
引言
鉴于永磁同步电机效率高、功率密度高、启停快速准确及调速范围宽等特点而被广泛应用于变频调速控制系统中[1-3]。内置式永磁同步电机由于其可靠的转子结构,过载能力强及调速范围宽等特性而越来越受到业界关注,大量用于机械手、机器人、混合动力汽车及智能设备等领域。
电感是永磁电机控制中重要的性能参数,电感的准确计算对其控制算法的实现以及系统性能的优劣均有直接的影响。考虑到永磁同步电机其转子永磁铁的凸极效应等,为更好的简化电机数学模型,提高控制精度,需将ABC轴系下的复杂电机数学模型转换到dq轴系下。基于此,精确计算dq轴系下的交直轴电感参数将显得尤为重要[4-6]。
随着有限元技术的发展,近年来,国内外研究人员广泛采用有限元仿真方法对永磁同步电机进行电感参数的计算分析。文献[2]采用冻结磁导率的仿真方法并考虑交直轴交叉耦合对内置式永磁同步电机进行了仿真研究,并进一步给出了交叉耦合对同步电机电磁转矩的影响规律。文献[3]基于内置式永磁同步电机研究了永磁体和电枢磁势共同作用下对其电感特性的影响,并提出了根据测量所得的电压及电流数据计算获得不同转子位置及电流下的磁链,之后通过该磁链获取所需的电感参数的一种改进的研究方法。文献[6]在研究永磁同步电机电感参数时,结合仿真与实验手段对比分析了忽略交叉饱和影响的有限元法以及冻结磁导率方法。文献[7]基于一定假设下同时求解了永磁电机交直轴电感,结果表明,直轴电感精度满足工程要求,而交轴电感由于直轴磁路等因素的影响其计算精度较差。文献[8]在气隙磁场基础上提出了一种计算同步电机电感参数的解析公式法,并通过实际样机验证了解析计算的有效性。
本文在永磁同步电机数学模型的基础上,结合最值法原理对电感参数进行了研究,并对比分析了仿真与实验结果。以现有12槽10极的分数槽集中绕组电机为例,采用最值法进行了仿真研究,仿真结果与实验结果一致性较高,误差在4 %以内,满足工程精度需求,同时研究了实际样机制作中由于定子内圆圆度导致的电感参数的变化规律。
1 永磁同步电机基本数学模型
永磁同步电机其定子结构类似于普通电励磁三相同步电机。如果永磁电机的永磁体和励磁电机的励磁线圈产生的感应电动势同为正弦时,则可采用电励磁同步电机的数学模型来分析永磁同步电机。
为简化分析,假设条件如下[9-10]:
1)转子上无阻尼绕组,磁钢无阻尼作用;
2)气隙磁场为正弦分布;
3)忽略铁芯材料的涡流及磁滞损耗;
4)不计铁芯饱和效应。
在上述假设下,结合图1所示的电机解析模型,可得永磁同步电机在三相静止坐标系UVW下其电压方程可以表示为:
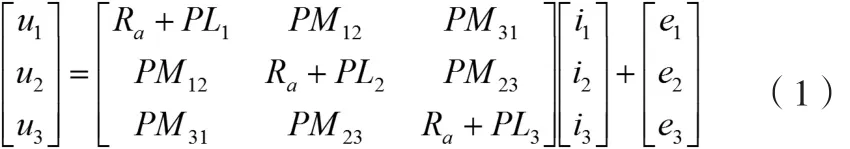
式(1)中:
u1、u2、u3分别为U、V、W相定子电压;
i1、i2、i3分别为U、V、W相定子电流;
Ra为定子绕组电阻;
L1、L2、L3分别为定子绕组自感;
M12、M23、M31为绕组间的互感;
P为微分算子;
e1、e2、e3分别为永磁体在U、V、W相电枢绕组中感应的旋转电势。
定子绕组自感满足:

式(2)中:
La1为定子绕组的漏感;
La0为定子绕组自感均值;
La2为定子绕组的二次谐波幅值。
绕组间互感满足:
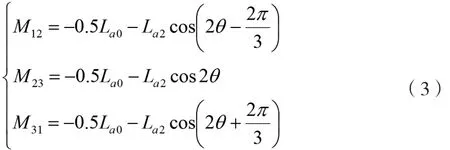
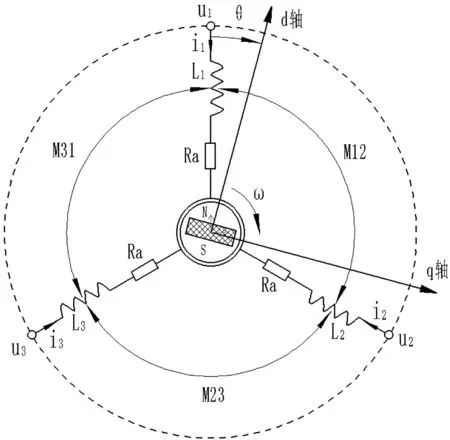
图1 永磁同步电机数学模型
与定子三相绕组交链的永磁铁磁链满足:
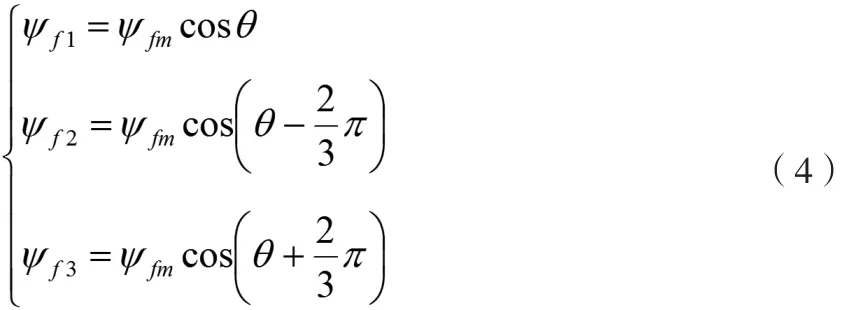
式(4)中:
ψfm为与定子三相绕组交链的永磁体磁链的幅值;
θ为U相绕组轴线与永磁体基波磁场轴线之间的电角度。
假设ω为电机转子的旋转角速度,则有:

此时,永磁体磁场在定子三相绕组中产生的旋转电势 e1、e2、e3满足:

模型中取d轴方向与永磁体基波磁场轴线的方向一致,即三相静止坐标系UVW的U轴与两相旋转坐标系dq的d轴间的夹角同为θ,则坐标系UVW与坐标系dq间的坐标变换矩阵为:

结合式(7)的坐标变换矩阵,将UVW三相坐标系下的电压方程式(1)转换到dq两相坐标系下,即:
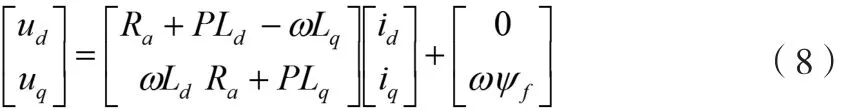
式(8)中:
ud、uq分别为d轴、q轴的定子电压;
id、iq分别为d轴、q轴的定子电流;
Ld、Lq分别为定子的绕组自感;

定子的绕组自感满足:
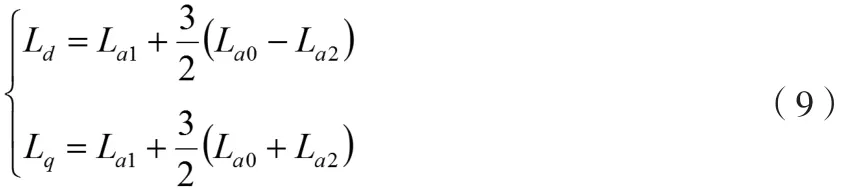
2 最值法电感测试原理
为获得式(9)所表达的电感结果,目前业界建立的测试方法多种多样,针对永磁同步电机,最值法操作便捷,易于实现,故本文采用最值法进行测试与仿真研究。图2为最值法原理。
在电机三相中任选两相,比如A、B相,按照图2接线,并通入对应交流电,慢慢移动转子,在不同测试位置处保持静止,记录每个位置处电压u、电流i及功率p的有效值,并筛选出最大和最小电压值,结合式(10)计算Lmax和Lmin,式(11)即为对应的d、q轴电感值。

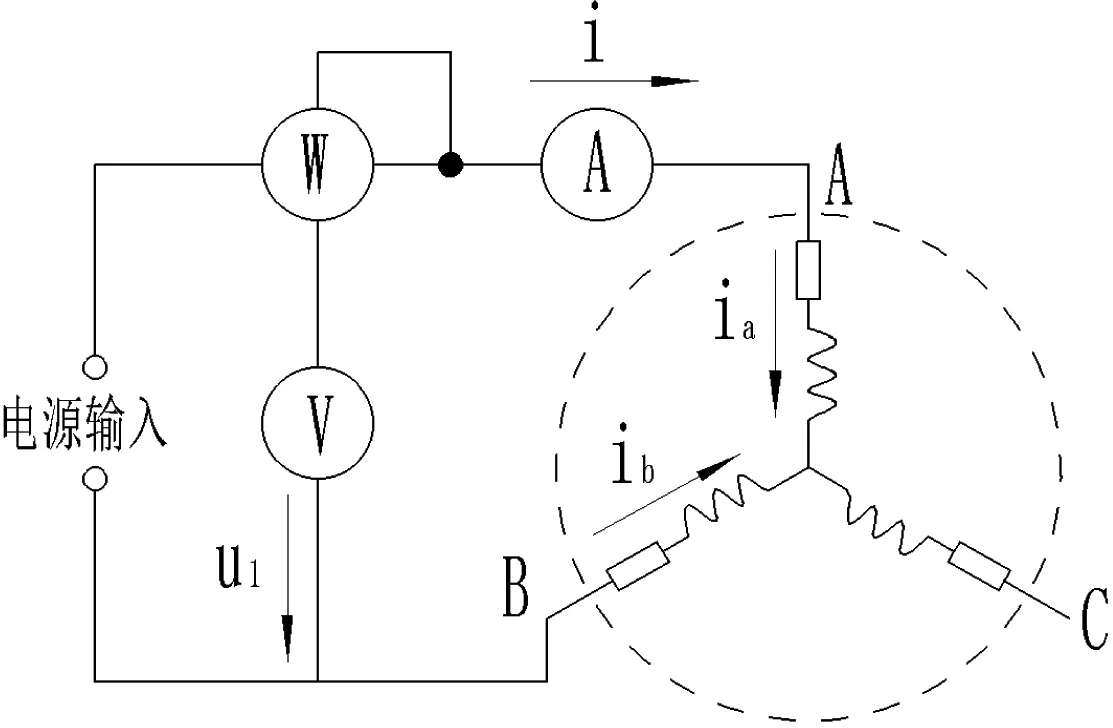
图2 最值法原理
3 最值法下交直轴电感计算分析
表1为现有12槽10极内置式型永磁同步电机基本参数,对其在maxwell2D中创建二维模型,如图3所示。
依据最值法测试原理在有限元软件中进行设置,外电路中通入交流电,仿真周期为1.25个电周期,转子相对定子的旋转角度θ变化范围为0~180 °。图4为电压随转子旋转角度的变化关系,图5为电感随转子旋转角度的变化关系。
由图4~5可知,随着转子旋转角度的变化,电感及输出电压均呈现周期性的变化规律。结合图5及式(11)可知,仿真所得该电机直轴电感Ld为1.094 mH,交轴电感Lq为1.285 mH。实测获得该电机的直轴电感Ld为1.12 mH,交轴电感Lq为1.33 mH。对比结果表明,d、q轴电感有限元仿真与实测结果一致性较高,仿真与实测误差均在4 %以内,满足工程精度要求。
4 定子内圆圆度对交直轴电感影响
在实际的样机试制过程中,发现由于定子采用分块拼装,容易出现拼装后电机定子内圆圆度较差的问题,永磁同步电机在很多应用场合对精度要求很高,因此为了更精确的控制电机,有必要掌握定子内圆圆度对电感参数的影响规律。
由表2及图6可知,定子内圆圆度主要影响d轴电感值,随着圆度不断的增大,d轴电感呈现一定的下降趋势,而q轴电感基本保持不变,分析结果为永磁同步电机的进一步研究与应用提供必要的参考依据。

表1 样机基本参数
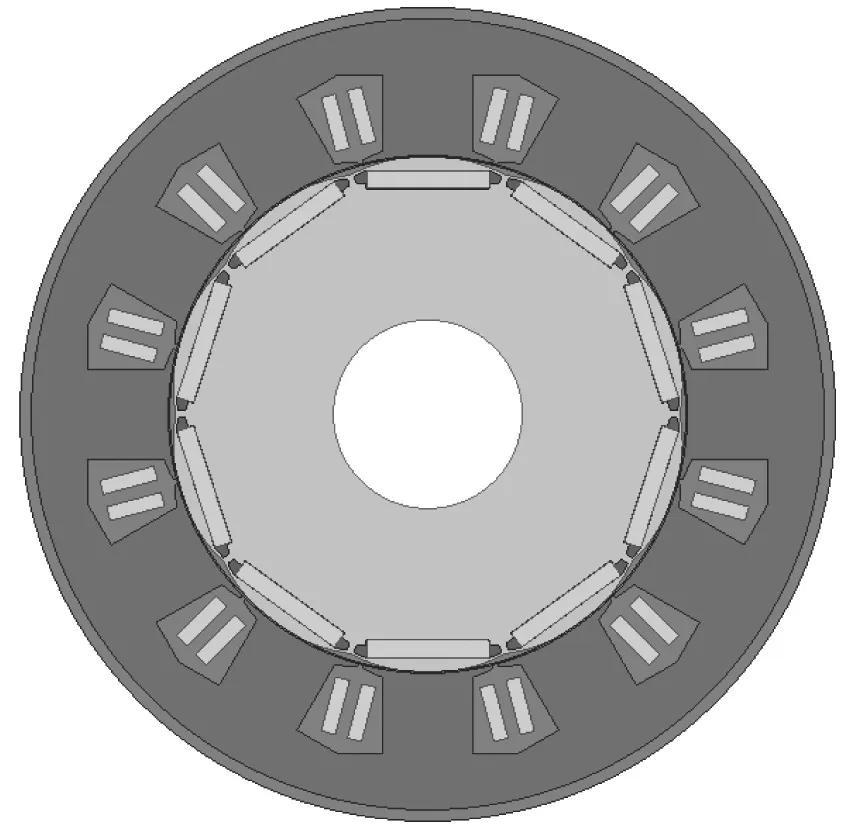
图3 内置式永磁同步电机模型
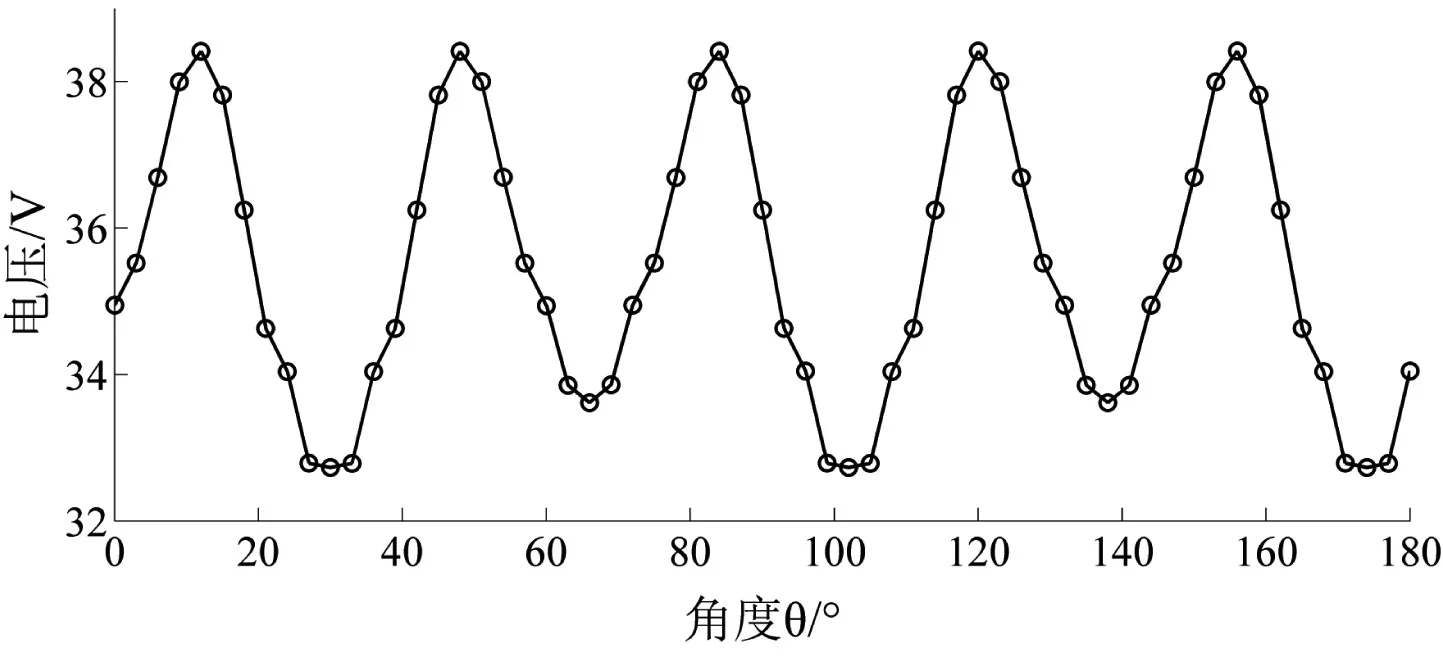
图4 电压随转子旋转角度的变化关系

图5 电感随转子旋转角度的变化关系

表2 定子内圆圆度对d、q轴电感的影响
5 总结
本文首先给出了永磁同步电机数学模型及最值法原理,然后基于最值法采用有限元仿真分析了12槽10极永磁同步电机电感,并与实测结果对比分析,同时研究了定子内圆圆度对交直轴电感的影响,结果表明采用最值法获得的交直轴电感其仿真与实测误差在4 %以内,满足工程精度要求;定子内圆圆度对d轴电感影响较大,而对q轴基本无影响。研究结果对于提高永磁同步电机性能有一定的参考依据与应用价值。

图6 电感随定子内圆圆度变化规律

