一种粒子群优化的SVM-ELM模型*

王丽娟，丁世飞

1.中国矿业大学 计算机科学与技术学院，江苏 徐州 221116

2.徐州工业职业技术学院 信息与电气工程学院，江苏 徐州 221140

1 引言

极限学习机（extreme learning machine,ELM）是一种简单、有效的单隐层前馈神经网络SLFNs学习算法[1]。只需设置网络的隐含层节点个数，在算法执行过程中，输入权值、隐含层偏置采取随机赋值的方式，通过最小二乘法得到输出层权值，产生唯一的最优解。由于ELM是基于经验风险最小化原理，随机输入权重和隐含层偏置，可能会导致部分隐含层节点无效[2]。因此ELM分类正确率的高低取决于隐含层的节点数，需要大量的隐含层节点来保证分类的精确度。和传统的基于梯度下降的学习算法相比较，由于ELM需要更多的隐含层神经元，这就降低其运算速率以及训练效果，为此人们提出了许多ELM的改进算法。

Huang等人基于递归最小二乘法（recursive least square，RLS)，提出了在线时序极限学习机（online sequential ELM，OS-ELM）算法[3]。之后，又提出了一种在线连续模糊极限学习机（online sequential-fuzzy-ELM，OS-Fuzzy-ELM）模型来解决函数逼近和分类的问题[4]。Rong等人针对原始的极限学习机由于分类网络的结构设计而导致的模式分类的低度拟合/过度拟合问题，提出了修剪极限学习机（pruned-ELM，P-ELM）作为ELM分类网络系统化和自动化的方法[5-6]。Silva等人对极限学习机进行了改进，提出利用群搜索优化（group search optimizer，GSO）战略选择输入权值和隐含层偏置的ELM算法，称为GSOELM方法[7]。这些优化方法，和ELM相比，都得到了很好的分类效果[8]。

20世纪90年代初，文献[9-10]提出支持向量机（support vector machine，SVM）。该算法建立在统计学习理论的基础之上，根据结构风险最小化原则提出的[11-12]，比神经网络更适合于小样本的分类，且泛化性能出色[13-14]。在模式识别、回归分析、函数估计、时间序列预测等领域都得到了发展，并被广泛应用于手写字体识别、人脸图像识别、基因分类等领域[15]。SVM通过核函数把低维空间的线性不可分问题转化为高维空间的线性可分问题，构造最优分类面，实现对数据样本的分类[15]。

ELM分类正确率的高低取决于隐层的节点数，但是大量的隐层节点使得ELM的结构很臃肿，而且容易导致内存不足。为了提高ELM单个节点学习能力和判断能力，本文利用支持向量机（SVM）来精简ELM，通过构建SVM-ELM模型，提高单个节点的判断能力。传统的参数选取都是经过反复的实验，凭借经验值来选取的，存在着很大的主观性；如果通过交叉验证的方式来选取参数，又会消耗大量的时间。本文为了使得SVM-ELM模型获得较好的分类准确率，利用PSO算法进行优化[16]，实现分类目标。

2 SVM-ELM模型

极限学习机（ELM）是2004年由南洋理工大学黄广斌教授提出，是单隐层前馈神经网络（single hidden layer feedforward neural network，SLFN）的一种[17-18]。传统的ELM算法随机确定隐层节点的权值wi和偏置bi，从实验结果来看，这种方法大幅度地节省了系统的学习时间，但是如果想要获得较好的分类效果，需要大量的隐层节点，而较少的节点则导致分类效果较差。这就表明，单个隐层节点的学习能力和判断能力不足，需要较多的节点来弥补，而节点的学习能力不足则是由于节点的线性决策函数的权值和偏置值随机决定造成的，使得节点欠学习[19]。如果能够提高ELM单个隐层节点的学习能力，那么即使较少的隐层节点也能获得较好的学习效果，ELM的网络结构就得以优化。SVM通过寻求结构化风险最小来提高泛化能力，基本思想是寻找最优分类面，使正、负类之间的分类间隔（margin）最大[20]。

由于ELM经验风险最小，以训练误差最小的准则来评价算法优劣，容易出现过拟合现象，影响分类模型泛化能力；一个好的分类模型在考虑结构风险和经验风险的同时还要对二者合理优化平衡，从而保证分类模型的泛化能力。本文将结构风险最小化的支持向量机（SVM）引入到极限学习机（ELM）中，提出一种ELM和SVM相融合的分类模式[21]。选取ELM为基础分类器，以SVM来修正改善分类效率。利用SVM来提高每个节点的判断能力，精简ELM的结构，提高其泛化性能。根据分类的类别数来确定层的节点数，改变传统的随机确定的方式，然后利用SVM来确定每个隐层节点的权值和偏置[22]，提高每个节点的学习能力和泛化能力。对于k类分类问题，SVMELM的隐层节点数为k，第i个节点的任务就是，利用SVM把第i类与其他的k-1类分开，根据SVM得到的训练结果得到每一个隐层节点的权值和偏置。

式（1）的对偶问题为：

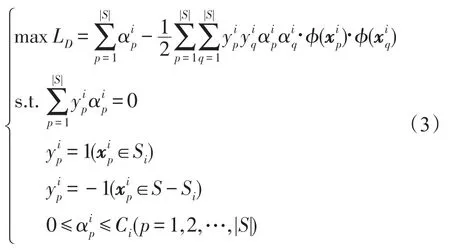
隐含层的输入矩阵表示为：

其中：

故：

其中，g(x)为ELM的激活函数。ELM常用的激活函数有Sigmoid函数、Sine函数、RBF（radialbasisfunction）函数等。本文选用效果较好的Sigmoid函数。则隐层节点数为k、激励函数为g(x)的SLFN模型为：

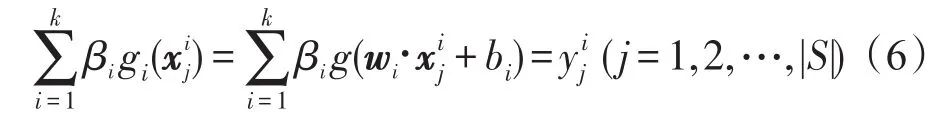
即学习系统为Hkβk=Y，学习参数：

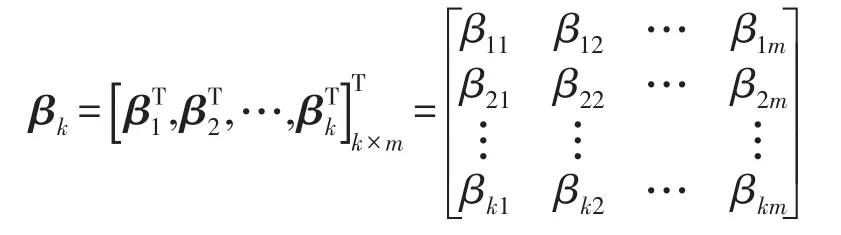
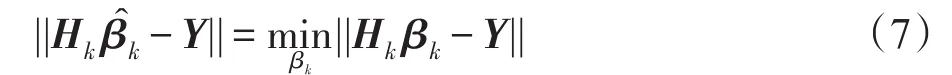
3 基于粒子群优化算法的SVM-ELM

文献[23]提出了粒子群优化算法（particle swarm optimization，PSO），该算法是一种启发式随机优化算法，在有限的迭代递推中快速搜索到全局最优解，该特性已被广泛地应用于数据挖掘和模式识别［20］等领域。支持向量机的参数选择直接影响到SVM模型的分类结果[24-26]。即使对于同一个分类问题，选择不同的SVM模型核函数、惩罚参数都将产生不同的分类结果。在实际应用中，为了获得性能更高的SVM分类器，则需要对SVM的各个参数进行优化调整[27]。因此，本文提出一种PSO-SVM算法，使用粒子群优化算法和支持向量机相结合的学习算法，即利用PSO算法的全局搜索能力对SVM的惩罚参数和核函数参数的取值进行优化调整[23]，避免选择局部最优的参数，使SVM的参数取值更具指导性，从而得到一个更精确的、分类效果优化的SVM分类器。文献[28-30]中阐述了PSO算法比人工神经网络（artificial neural network，ANN）、遗传算法（genetic algorithm，GA）实现更简单，使用参数更少。

基于PSO全局搜索对SVM参数全局寻优的PSO-SVM-ELM模型训练流程图如图1，详细处理步骤如下：

步骤1数据预处理。优化算法通过已知数据集随机产生训练集和测试集进行训练来获得SVM模型。

步骤2初始化粒子群的粒子数、最大迭代次数、每个粒子的初始位置、速度初值、个体最优位置和全局最优位置等，以及SVM的参数C和RBF核函数的宽度参数σ。

步骤3通过交叉验证算法PSO在全局空间搜索粒子最优解，获得SVM模型惩罚参数、核函数参数的最优值。

步骤4将训练数据集带入SVM训练得到PSOSVM训练模型。

Fig.1 PSO-SVM-ELM model flowchart图1 PSO-SVM-ELM模型流程图

步骤5用测试数据集验证PSO-SVM模型的处理能力，得到优化了的PSO-SVM模型。

步骤6根据分类类别确定隐含层节点数，利用PSO-SVM模型训练，获得ELM每个隐含层节点的权值和偏移。

步骤7根据隐含层节点数k及激活函数sigmoid函数得到学习系统模型，求解学习参数。

步骤8获得高精确度的分类模型PSO-SVMELM。

其中，利用PSO算法优化SVM参数的详细过程如图2，详细步骤为：

步骤1获得训练数据集，组建粒子群；设置SVM参数搜索范围。

步骤2初始化粒子群参数包括粒子数量、最大迭代数、粒子群初始位置和速度初值以及每个粒子个体位置最优pbest和群体位置最优gbest等，初始化SVM模型参数C和RBF核函数的宽度参数σ。

步骤3更新pbest和gbest并记录粒子的适应值。

步骤4更新粒子群中粒子的位置和速度。

步骤5若达到最大迭代次数或找到最优解，则算法结束，转向步骤6，否则转向步骤2，继续求解。

Fig.2 PSO-SVM model flowchart图2 PSO-SVM模型流程图

步骤6输出SVM模型的惩罚参数C和RBF核函数的宽度参数σ的全局最优值，算法结束。

利用粒子群优化算法对SVM-ELM模型中的参数进行自动选择，克服了人为选择的主观性，避免了人为尝试浪费过多的时间，同时通过设置粒子适应度函数可以实现控制参数选择的方向的目的[31-33]。

4 实验分析

为了验证基于粒子群算法的SVM-ELM模型的有效性，从UCI机器学习数据库中选取了4个用于分类的数据集葡萄酒质量数据集Wine、小麦种子数据集Seeds、Balance Scale以及CNAE-9进行实验，数据描述如表1所示。

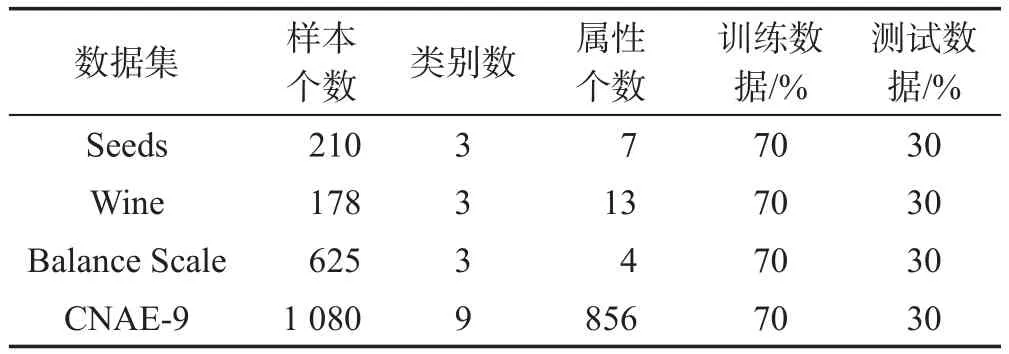
Table 1 Description of data sets表1 数据集描述

在SVM-ELM模型中，运用SVM模型求解过程来优化ELM隐含层节点的权值和偏置时，SVM的核函数有多种：径向基核、多层感知器核等。根据实验结果，本文选择了径向基核函数，即；ELM激活函数选择性能较好的Sigmoid函数，即g(x)=1/(1+e-x)。

基于粒子群算法的SVM-ELM模型中，待优化的参数为RBF核函数的宽度参数σ、惩罚参数C。这三类数据集的种群大小以及参数搜索范围的取值如表2所示。

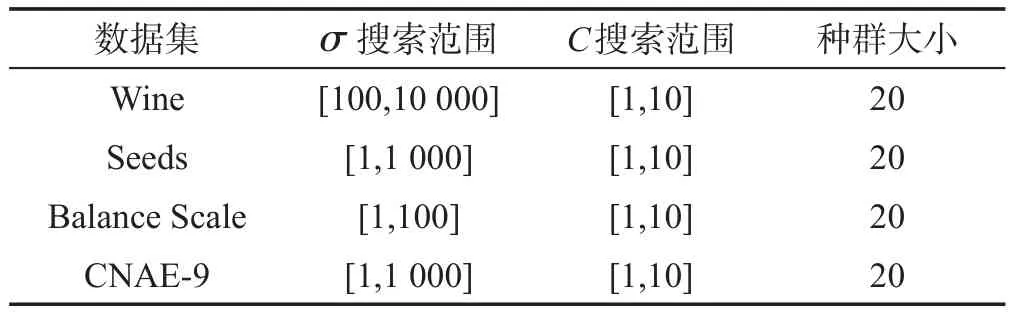
Table 2 Value of PSO parameters表2 PSO参数的取值

粒子群的加速因子c1=c2=2，种群的规模m=20，惯性权重w=0.9，最大迭代次数为2 000。实验环境：Intel®Xeon®CPU E3-1225 V2@3.20 GHz处理器，4 GB RAM，32位操作系统，Matlab R2012b。PSO算法在经过多次迭代之后，每个数据集获得的参数σ和C如表3所示。

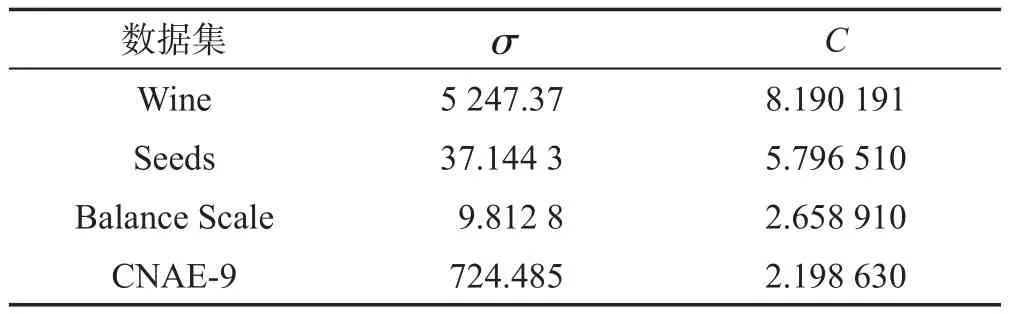
Table 3 Parameter value of PSO-SVM-ELM model表3 PSO-SVM-ELM模型参数值

数据集 Wine、Seeds、Balance Scale、CNAE-9 的gbest值随着飞行路径的变化分别如图3～图6所示。从图中可知针对这4个数据集，PSO算法具有较强的收缩能力，都能最终找到全局最优值，可以有效地解决SVM参数优化问题。

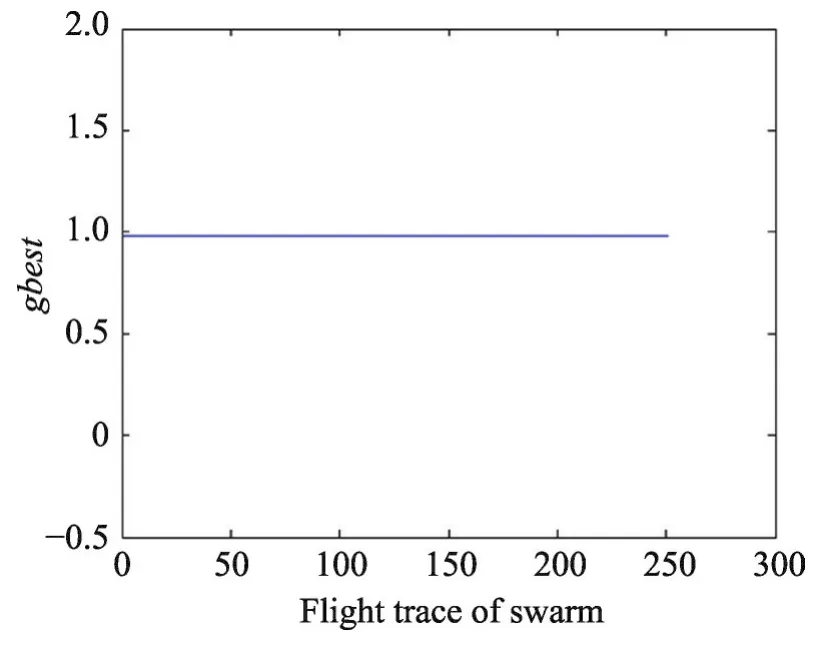
Fig.3 Flight trace of global optimal value of Wine data set图3 Wine数据集全局最优值的飞行路径

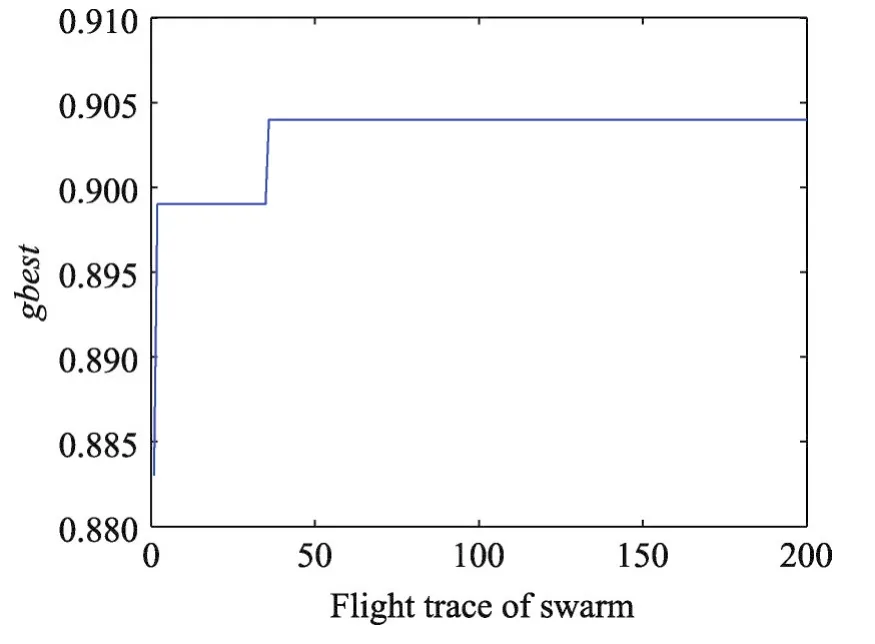
Fig.5 Flight trace of global optimal value of Balance Scale data set图5 Balance Scale数据集全局最优值的飞行路径

基于粒子群优化的SVM-ELM模型的分类结果如表4所示。

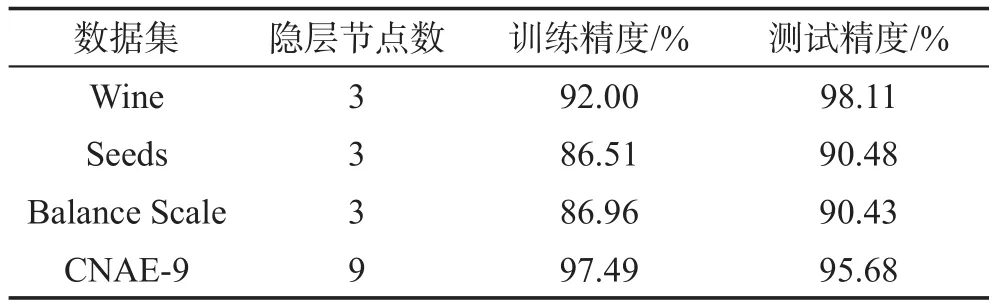
Table 4 Classification results of PSO-SVM-ELM model表4 PSO-SVM-ELM模型的分类结果

通过不断的尝试、实验，根据分类效果确定SVMELM模型的参数。Wine、Seeds、Balance Scale数据集均有3类数据，故这3类数据集的SVM-ELM模型的隐层节点数均为3。而CNAE-9数据集的数据类别为9，故隐层节点数为类别数9。SVM-ELM分类结果如表5所示。

Fig.4 Flight trace of global optimal value of Seeds data set图4 Seeds数据集全局最优值的飞行路径

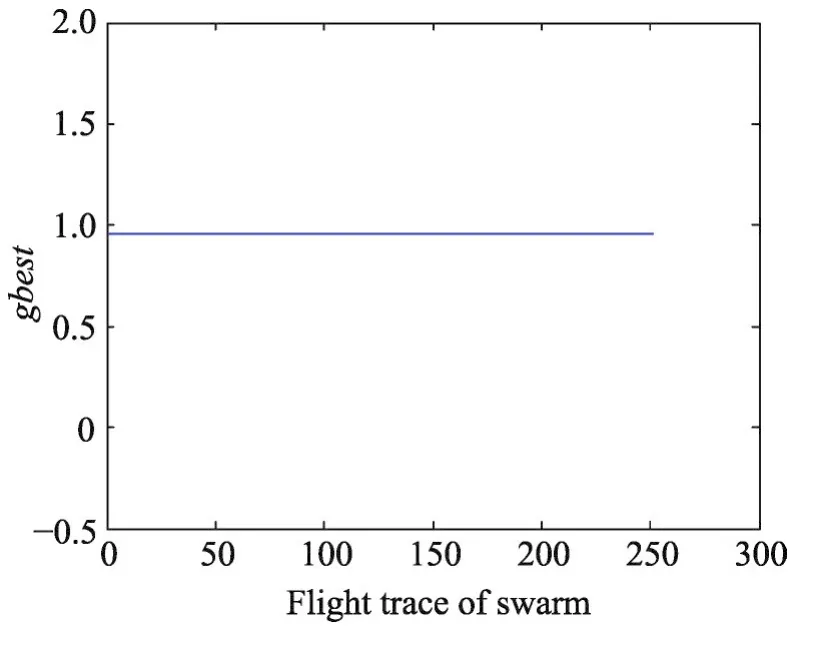
Fig.6 Flight trace of global optimal value of CNAE-9 data set图6 CNAE-9数据集全局最优值的飞行路径

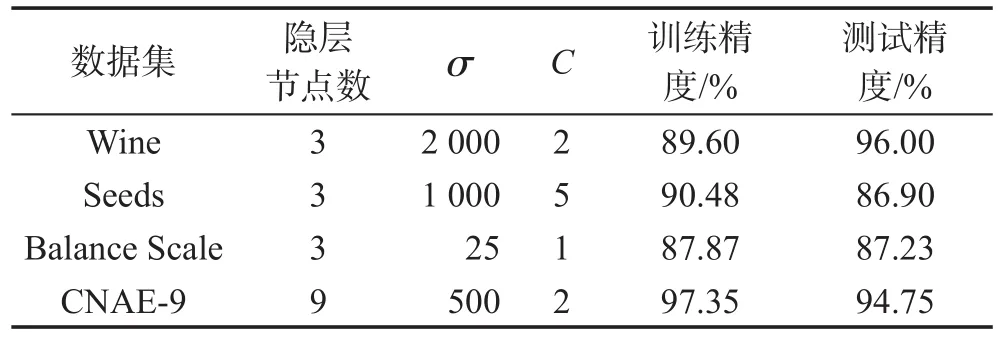
Table 5 Experimental results of SVM-ELM表5 SVM-ELM的实验结果

在设置不同的隐层节点数的情况下，ELM的分类结果如表6所示。表6中所列出的数据是在隐层节点数确定时，重复10次实验，选择其中测试精度的最大值作为最优值。

Table 6 Experimental results of ELM表6 ELM的实验结果

在Wine数据集上，随着隐层节点数的增多，ELM的测试精度不断提高；在Seeds、CNAE-9数据集上，随着隐层节点数目的增多，ELM的测试精度出现局部的波动，但整体依然是不断提高的。这表明ELM的学习效果和隐含层的节点数有很大的关系，要想达到良好的学习效果，必须有足够多的隐层节点，导致网络规模很臃肿。在Balance Scale数据集上，随着隐层节点数目的增多，ELM的测试精度出现先逐渐提高，然后下降的情况，这说明ELM的稳定性较差，且容易出现过拟合的现象。

比较表4～表6可以发现，本文提出的PSO-SVMELM模型在这4个数据集上的测试精度均高于SVM-ELM和ELM。其中在Wine数据集上，PSOSVM-ELM的测试精度高于SVM-ELM模型的测试精度2.11%，高于ELM的最高精度5.66%；在Seeds数据集上，PSO-SVM-ELM的精度高于SVM-ELM模型的测试精度3.58%，高于ELM的最高精度5.96%。PSO-SVM-ELM、SVM-ELM和ELM对于所选取的数据集的分类正确率的比较如表7所示。

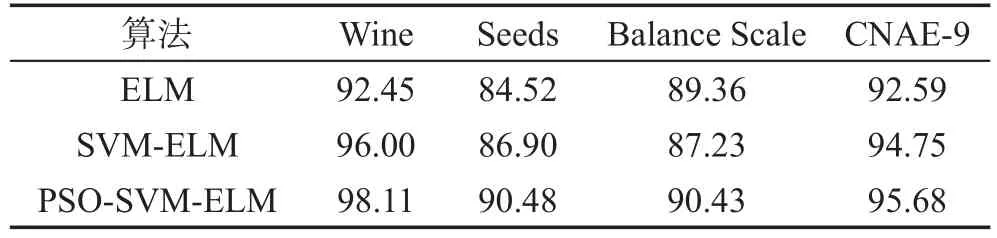
Table 7 Comparison of experimental results表7 实验结果对比 %

SVM-ELM的参数确定经过了多次的尝试，浪费了大量的时间，并且没有找到最优值。而ELM达到最高精度的隐层节点数分别为5 000、1 000、20、300，也经历了无数次的尝试。ELM的结果极不稳定，且容易出现过拟合的现象。而PSO-SVM-ELM的隐层节点数仅仅为数据集中的数据类别数，网络稳定，不会出现过拟合的现象，并且可以很方便地就可以找到最优值。

5 结论

本文提出了基于粒子群算法优化的SVM-ELM模型，即PSO-SVM-ELM模型，通过SVM确定ELM的隐层节点的权值和偏置，然后利用粒子群算法（PSO）来优化SVM-ELM的参数。PSO-SVM-ELM模型在提高极速学习机的泛化性能的同时精简了ELM，使得在隐层节点数为待分类数据集的类别数时，能够达到很好的分类效果，实验足以说明基于粒子群优化的SVM-ELM模型在进行数据分类时是比较理想的。