爆炸作用下RHT模型参数敏感性分析∗

辛 健

（91550部队 大连 116023）

1 引言

开展舰载武器系统对陆攻击毁伤评估研究是靶场面临的一个重要研究方向。由于真实的毁伤试验成本高，因此不能通过大量的重复的试验来获取充分的数据。近年来，数值模拟方法已成为毁伤效应研究的重要技术手段之一，但数值模拟的准确性，与选用的本构模型及其参数直接相关。对于机场跑道、指挥所等重要打击目标，研究其主要构成材料的动态力学性能是进行数值模拟的关键［1～2］。混凝土RHT本构模型［3］综合考虑了混凝土失效面的压力相关性、压缩损伤演化、应变率效应等特点，同时引入了偏应力张量第三不变量对失效面形状的影响，并考虑了拉、压应变率效应的差异，因而被广泛应用于混凝土动态响应过程的数值模拟［4～7］。

选定本构模型后，需要确定本构参数，通常采用理论分析和力学试验结合的方法来获取参数［8～11］。针对某一特定的动态响应过程，借助于参数敏感性分析，可以评估参数对计算结果的影响程度，确定参数的敏感度，从而为数值模拟提供参考依据，对力学试验方案进行优化设计。本文基于参数敏感性分析方法，开展了混凝土内部爆炸的数值模拟，对RHT本构模型参数的敏感性进行了初步分析。

2 敏感性分析方法

敏感性分析是系统分析中分析系统稳定性的一种方法［12］。设有一系统，其系统特性P由n个因素 a=｛a1，a2，…an｝决定，即 P=f（a1，a2，…an）。在某一基准状态下，系统特性为 P*。分别令各因素在一定的变化范围内变动，分析由于因素变动，系统特性偏离基准状态的趋势和程度，这种分析方法称为敏感性分析。

进行敏感性分析，首先需要确定基准参数集，具体分析参数ak对系统特性的影响时，可令其余参数取基准值且固定不变，而令ak在一定的范围内变动，此时系统特性表现为进而考察单个参数对系统特性的影响。

以上分析仅能了解系统特性对单因素的敏感行为，在实际系统中，决定系统特性的各因素往往是不同的物理量，量纲各不相同。凭借以上分析，无法对各因素之间的敏感程度进行比较。因此，有必要进行无量纲化处理。为此，我们定义了无量纲形式的敏感度函数和敏感度因子。即将系统特性P的相对误差：

与参数ak的相对误差：

的比值定义为参数ak的敏感度函数S（kak）：

通过对Sk的比较，就可以对系统特性对各因素的敏感性进行对比评价。

3 RHT模型参数敏感性分析

RHT本构模型由Riedel等［1］于1999年提出，强度描述方面，模型引入了三个失效面，即最大失效面、弹性屈服失效面和残余失效面，它们分别描述混凝土的失效强度，初始屈服强度及残余强度的变化规律。状态方程方面，模型采用了考虑多孔度α影响的p-α 状态方程［13］。

图1 TNT在混凝土中爆炸模拟

利用 ANSYS/AUTODYN 有限元软件［14，采用RHT本构模型，进行了TNT装药在球形混凝土内部爆炸的数值计算，计算模型如图1所示。计算采用2D轴对称模型，TNT位于球心，混凝土采用Lagrange算法，炸药采用Euler算法，欧拉网格包含了靶体中受爆炸影响较大的区域，Euler/Lagrange耦合方式选择自动模式，能量容差值为0.05。

以爆炸后混凝土内部损伤区域面积作为系统特性，考察RHT模型各个本构参数对数值计算结果的影响，进而分析参数的敏感度，取软件材料库中35MPa混凝土默认参数为基准参数，其中，拉伸失效选择主应力失效模式，PTFS（Principle Tensile Failure Stress）基准值取3.5MPa，断裂能Gf基准值取120J/m2，其余参数均取默认数值。为了便于分析比较，将全部参数进行排序编号，如表1所示。

表1 RHT模型参数

首先采用基准参数进行计算，得出装药爆炸后混凝土内部的损伤情况，如图2所示。当损伤面积不再扩大时，进行损伤面积的判读，为了量化方便，选取损伤度D为1.0的区域（图2中虚线内区域）面积为损伤面积S0，S0即为基准状态下的系统特性。为了考察RHT模型参数ak（k=1，2，…，31）对损伤计算面积的影响，调整参数ak的数值为其基准数值的80%，即参数ak的相对误差dak=0.2，其它参数仍取基准值，计算得出损伤面积Sk。依此方法，可计算得出RHT模型每个参数单独改变dak=0.2时，对应的损伤面积。

图2 爆炸后混凝土损伤情况

由式（1），可得出由于参数ak的变化引起损伤面积Sk的相对误差：

由式（3），可得出参数ak的敏感度函数S（kak），如表2所示，参数敏感直方图如图3所示。

从敏感性分析结果可以看出，RHT模型各个参数对计算结果的影响各异，敏感度较高的参数包括：单轴拉压强度比ft/fc，拉压子午比Q0，剪压强度比 fs/fc，残余强度参数 B、M，最小塑性应变 Ef，min，单轴抗压强度fc，失效面强度N，如表3所示。表3以外的其他参数敏感度都小于0.25，即该参数变化20%时引起的结果变化小于5%，对计算结果影响较小。值得注意的是，在本文的数值计算中，参数pcrush、plock、cporous和n敏感度为0，即这些参数的变化对计算结果几乎没有影响。

表2 敏感度函数S（kak）

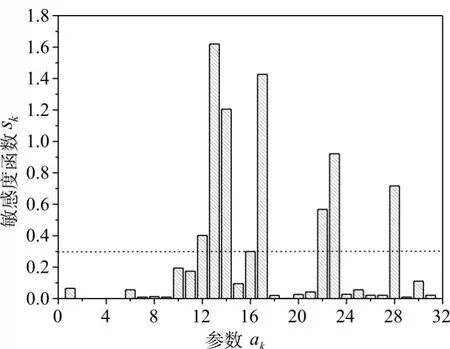
图3 参数敏感度直方图

通过参数敏感性分析，得出了参数敏感度。分析结果可为其它数值模拟工作提供参考，为确定本构模型参数的力学试验方案优化设计提供参考依据，针对敏感度高的参数细化试验方案，提高试验数据的准确度，从而提高参数的准确度，从参数角度降低数值模拟的误差，提高计算结果的准确度。

表3 敏感度较大的参数

4 结语

准确合理地选取材料本构模型参数是目标动态力学响应过程数值模拟的关键问题，了解参数变化对计算结果的影响程度具有实际意义。本文在单因素敏感性分析的基础上，定义了无量纲形式的敏感度函数，进行了混凝土内部爆炸过程的数值模拟，确定了爆炸过程混凝土RHT本构模型参数的敏感度。其中，敏感度较高的参数包括：单轴拉压强度比 ft/fc，拉压子午比 Q0，剪压强度比 fs/fc，残余强度参数B、M，最小塑性应变Ef，min，单轴抗压强度fc，失效面强度N。通过参数敏感性分析和敏感度因子排序，可为其它动态响应过程的数值模拟提供参考，并可以针对不同的具体情况，确定符合实际的主要参数和次要参数，对参数获取的试验方案进行优化设计，从而提高数值模拟的准确度。