金属机身飞机框间距及截面参数分析

马骏

(上海飞机设计研究院 飞机结构强度工程技术所, 上海 201210)

0 引 言

隔框的间距对机身受压蒙皮壁板的设计有非常大的影响。同时隔框的间距对壁板的重量也有较大影响，随着隔框间距的增大，固定在隔框上的地板梁的跨度也会增大，必然导致地板结构重量的变化。

目前国内外资料基本没有对于框距初步确定的设计分析，都是以经验值20 in[1]作为说明，Hans-Jürgen Schmidt[2]研究了典型金属隔框的设计原则并分析了隔框截面形式的选择；邓扬晨等[3-4]研究了军用飞机加强框的拓扑优化设计以及小型飞机普通隔框的设计优化方法；陈振兴等[5]研究了民用飞机隔框与蒙皮壁板的连接结构；姜晓伟[6]研究了隔框的逆向设计和数字化加工。但以上研究都偏向于研究单一隔框，并未对隔框间距做过多分析。

本文从稳定性、强度、重量三方面分析框距初步设计值的确定方法，同时对飞机普通隔框的截面形式进行结构参数分析，以期为后期的详细设计阶段提供参考。

1 框间距初步设计分析

1.1 结构稳定性约束

对于飞机机身结构，机身隔框的间距需要保证在设计载荷下，隔框间的壁板不发生失稳。一般民用飞机的机身中间等直段为横截面近似圆形的薄壁加筋结构。在分析圆柱筒壳的弹性稳定问题时，可以取单位周长的一条壳壁，将其看作是两端受轴向压力作用而沿长度支承在弹性基体上的细长板条，当压力增大到一定数值时，此板条在直线形态下平衡，就丧失了稳定性，而可能在波纹状的微弯状态下维持平衡。因此可以选取一段单位周长壁板作为分析模型，如图1所示。

上述模型的稳定问题可以利用欧拉公式(式(1))进行计算分析。

(1)

Iz为所取模型截面惯性矩，其计算过程如下所示。

首先，计算形心位置，得到中性轴位置。

yc

(2)

A2=l·t2

(3)

A1=h1·t1+2(b1-t1)t1

(4)

A=A1+A2

(5)

(6)

(7)

然后，计算截面惯性矩

Iz=Iz1+Iz2+Iz3+Iz4

(8)

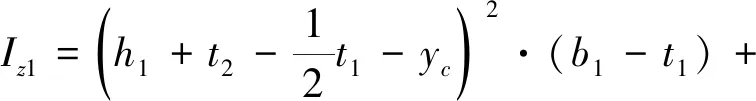
(9)

(10)

(11)

(12)

将以上各式代入欧拉公式，有

(13)

计算采用Lskin=10 m等直段机身简化模型，不考虑窗框等开口以及地板等部件的影响，参考150座级飞机数据，设计h1=28 mm，蒙皮厚度根据气密压差计算(设计载荷下，考虑急速气动引起的压差变化以及安全系数，取2倍压差载荷)，根据计算分析，本文取蒙皮厚度t2=1.2 mm，取飞机极限弯矩M=6.5×109N·mm，机身半径R=2 000 mm。长桁数量设为86根，计算模型的简化蒙皮段长度l=145 mm，各部件材料为2024-T3铝合金。代入式(13)，得到含有框距的一个约束函数。

(14)

1.2 结构强度约束

在强度方面，在机身最上端，弯曲正应力最大，因此根据强度条件有

(15)

式中：[σ]=271.94 MPa

代入数据得到t1和b1的约束函数：

28t1+2(b1-t1)t1>97.90

(16)

1.3 质量计算

飞机结构设计以重量最轻为目标，因此隔框间距以及长桁截面参数的确定要在满足约束函数的情况下，使得结构重量最轻。

机身质量计算如下：

M=Mskin+Mstringer+Mframe

(17)

Mskin=2πR·Lskin·ρ=0.35 t

(18)

Mstringer=nstringer·A1·Lskin·ρ

(19)

(20)

式中：Aframe为隔框的横截面积。

Aframe的变化并不影响本节所分析的内容，因此，根据某型民用飞机将Aframe设为定值，令Aframe=220 mm2，由此得到

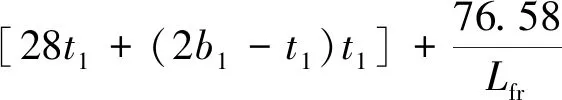
(21)

1.4 结果分析

根据式(14)、式(16)、式(21)绘制隔框间距与机身段重量的关系图，如图2所示，可以看出：机身段与隔框间距呈现一定的关系，左侧为以拉伸强度为约束条件的曲线，此时由于拉伸静强度的限制，面积A最小值不会有变化，则蒙皮加筋板的重量不会变化，图中的重量变化是由于隔框间距增大，导致隔框数量减少从而引起整体重量的降低；隔框间距继续增大后，约束条件转变为失稳条件，此处长桁的翻边宽度，长桁厚度，隔框间距均在变化，综合作用导致重量的变化。在约束条件切换的地方出现机身重量的最小值，因此，在这个地方附近取设计值接近最优设计值，其设计参数为Lfr=516 mm。

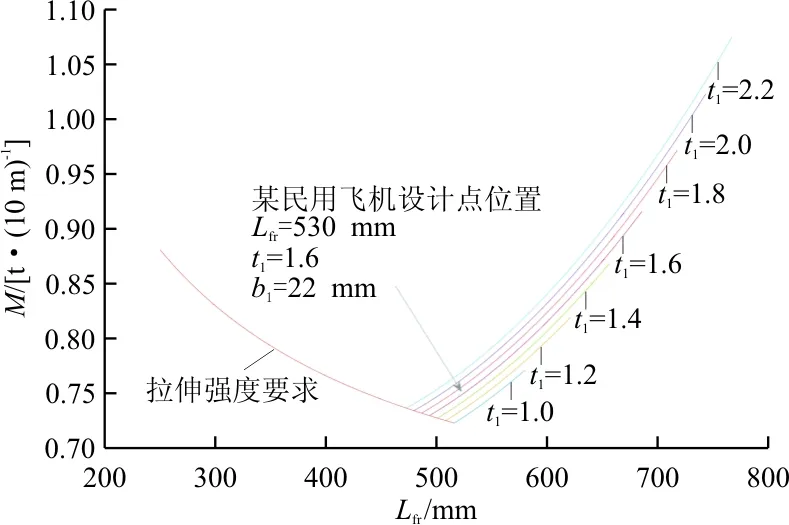
图2 机身段质量与隔框关系图

图2是经过合理简化得出的，没有考虑地板组件对失稳的有利影响，因此根据图2得到的设计点是偏于保守的设计点。上述设计点可以作为初始设计点，在综合考虑其他各方面因素以及机身结构的具体情况进行调整，例如：内部各种设备的安装，维护维修的开口，系统管路的要求等。

一般150座级飞机设计经验值为20 in (508 mm)，与本文分析计算值相符。对于其他构型尺寸的飞机，初始设计值应根据具体情况具体对待，仍可按照本文的设计方法定出初始设计值。

2 隔框结构尺寸分析

座舱普通框和加强框在机身的径向对座舱壳体的膨胀有很大的约束作用。普通框的主要作用是保持机身的外形，防止蒙皮壁板在纵向压缩载荷作用下发生弹性失稳[7]。

2.1 隔框尺寸初步分析

上文分析了隔框的间距使得机身筒体不发生框间的局部失稳，即使如此，机身筒体仍有可能发生跨框的总体失稳，普通框的结构剖面尺寸主要取决于框的结构刚度不会引起机身的总体失稳，即最小机身框面内弯曲刚度要求。为了防止机身壳体在承受弯曲时出现总体失稳，所需要的隔框刚度为

(22)

通过对已有试验数据的研究发现Cf的值为1/16 000[4]，则有

(23)

代入数据计算，得

If≥1.74×105mm4

(24)

为了方便分析，本文分析简化的隔框直接与蒙皮壁板相连的结构形式，不讨论“浮框式”结构，普通隔框示意图如图3所示。

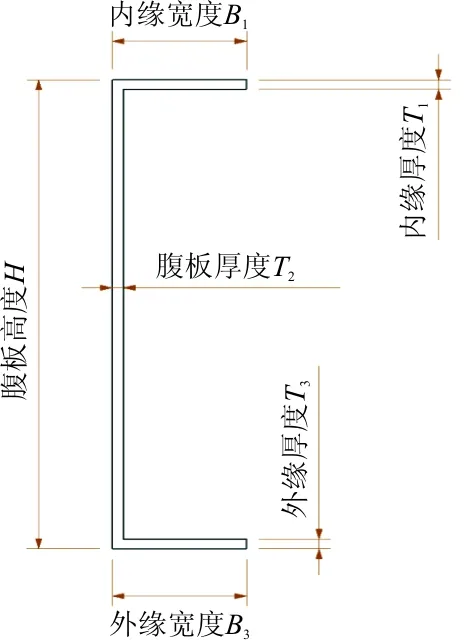
图3 隔框截面示意图

计算可得

(25)

Af=H·T2+(B1-T2)·T1+(B3-T2)·T3

(26)

对于隔框截面来说，从获得高截面惯性矩的角度，腹板应该越薄越高，缘条应越厚越短，但是腹板太薄以及缘条宽度太小容易造成侧向失稳，同时腹板太高会造成内部空间的减少，这会极大地降低乘坐空间舒适性。

初步设计时，假定T1=T2=T3=1.6 mm，且令B1=B3，由此得到：

If=0.133H3+0.683B1+3.2(0.5H-0.8)2×
(B1-1.6)

(27)

将式(27)代入式(24)得到一个可行域，如图4所示。

图4 隔框参数可行域

在可行域内边界选取若干组合数据，计算截面面积Af以及侧向弯曲截面系数Iy，如图5所示。

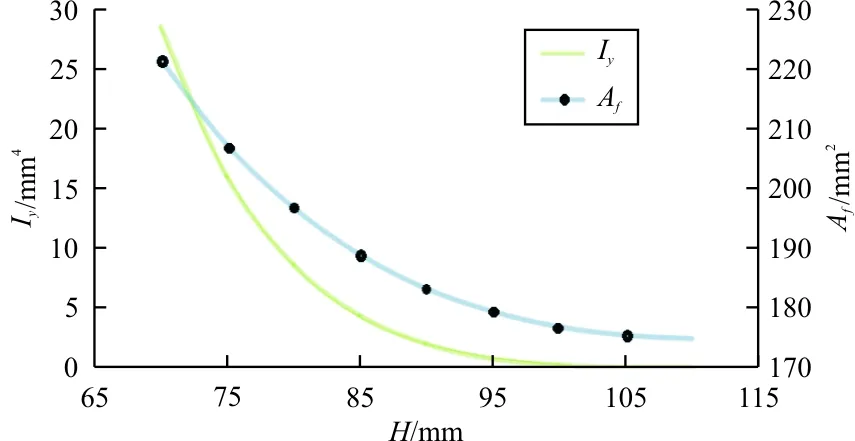
图5 隔框腹板高度影响曲线

在确定隔框截面初步参数时，根据以上分析，参数选取应该使Af尽量小从而重量小，且Iy又不能太小以防止侧向失稳，可初步确定H=80～95 mm，从而B1=B3=15 mm。

2.2 格框尺寸参数DOE分析

上文分析了150座级民用飞机隔框间距取值的初步分析方法以及机身普通隔框截面尺寸值初步确定方法。本节通过有限元分析机身普通隔框各个参数对隔框约束条件的重要性，进一步确定隔框的截面参数。使用Isight[8-9]试验设计(Design of Experiment，简称DOE)模块进行设计分析，自动循环计算隔框结构各尺寸因子对约束的影响。计算模型选取长10 m，半径2 m的等直段筒段模型，载荷工况为2倍气密载荷的极限工况，约束条件为蒙皮壁板应力水平。以隔框内缘条厚度、内缘条宽度、外缘条厚度、外缘条宽度、腹板厚度以及腹板宽度6个参数作为变量因子，如表1所示。

表1 参数提取汇总表

对Isight的DOE模块进行相应设置，采用最优拉丁超立方设计方法进行DOE分析计算，计算结果如图6所示。图中颜色表示变量因子与目标约束呈负相关的关系，隔框各项参数的增大皆会导致蒙皮应力的降低。定量分析各参数对蒙皮应力S的相对影响，如表2所示。

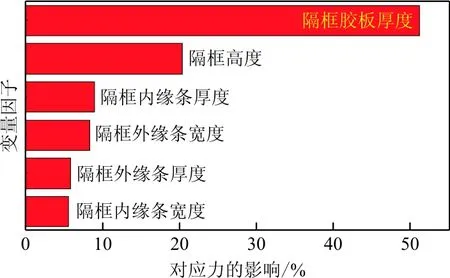
图6 DOE分析结果示意图

参 数对S的相对系数隔框内缘条厚度-0.17隔框外缘条厚度-0.06隔框腹板厚度-0.88隔框高度-0.40隔框内缘条厚度-0.15隔框外缘条厚度-0.17

从图6和表2可以看出：隔框腹板厚度对蒙皮应力的影响最大，其次是隔框高度，隔框内缘条宽度影响最小。由此可得，在2倍气密设计载荷工况下，隔框腹板的厚度对蒙皮应力的影响占主导地位。但是腹板厚度的增加容易造成隔框整体重量的增加，而隔框抗弯截面系数对于腹板厚度值并不敏感，因此一般通过调整隔框的高度，隔框高度对蒙皮应力水平影响较大，同时隔框高度对隔框抗弯截面系数影响也较大。另外DOE分析结果显示隔框外缘条宽度的影响大于内缘条宽度，且外缘条还需要与蒙皮壁板进行连接，因此设计时隔框外缘条宽度应大于内缘条宽度。

DOE分析结果可为后期详细设计优化阶段作参考，影响大的参数作为优化变量，影响小的参数选取常量，以节省优化资源[10]。

3 结 论

(1) 提出了一种简化计算模型，即选取蒙皮壁板单位周长壁板截面，以静强度和局部稳定性为约束条件，计算出隔框间距初步设计值，并与现有民用飞机隔框间距设计经验值20 in(508 mm)比较，结果吻合很好。

(2) 分析了普通隔框截面参数初步设计方法，对150座级飞机给出了隔框截面参数可行域，初步确定H=80～95 mm，从而B1=B3=15 mm。

(3) 分析了隔框各个参数对于蒙皮应力的影响大小，初步确定隔框外缘条宽度的影响大于内缘条宽度，且外缘条还需要与蒙皮壁板进行连接，因此设计时隔框外缘条宽度应大于内缘条宽度。