基于精英保留策略的改进蝙蝠算法及其在车辆路径问题中的应用

(武汉理工大学自动化学院 湖北 武汉 430000)

一、引言

经典的车辆路径问题(Vehicle Routing Problem，VRP)最先由G.Dantzig和J.Ramser[1]在1959发表的《The Truck Dispatching Problem》一文中提出。VRP问题为NP难问题，其一经提出，便引起了众多学者的研究，VRP问题被分成了许多类型的问题。比如作为VRP问题经典分类的带时间窗的车辆路径问题(Vehicle Routing Problem with Time-Window，VRPTW)，其由Solomon[2]在1979年首次提出，随后便受到广大学者的关注，顾名思义，其在原有的基础上多了一个时间窗的要求。其根据对时间窗要求的严格与否又被分为硬时间窗和软时间窗，本文仅考虑硬时间窗的情况，即严格遵守时间窗，车辆要在各客户点的最晚受理服务时间前到达。

二、问题的模型

VRPTW问题一般被描述为：假设配送中心(此处用0表示)最多可以以K辆车对L个客户进行配送运输服务，配送运输车辆的载重量上限分别为qk(k=1,2,…,K)，每个客户的货物需求量分别为gi(i=1,2,…,L)，cij为客户点i和客户点j之间的距离(i、j=1,2，…，L，且i≠j)，同时，记车辆到达客户点i的时间为RTi，车辆在客户点i处理服务(卸货)的时间为UTi，tij为车辆从客户点i到客户点j所需时间，客户点i要求的时间窗为[ETi,LTi]。要求配送中心计划用最短的总行驶距离或运输费用完成对所有客户的配送任务。

首先定义客户点的编号集合H={1,2,…,L}、配送路线的编号集合C={0,1,…,L}和配送车辆的编号集合V={1,2,…,K}，其中L为总客户数，K为配送中心的最大可用车辆数。则VRPTW问题的模型[5]如下：

(1)

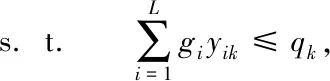
(2)

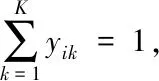
(3)

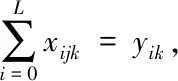
(4)

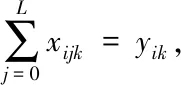
(5)

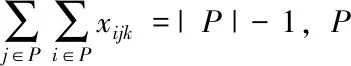
(6)

ETi≤RTi≤LTi,i∈H

(7)

xijk∈{0,1},∀i、j∈H,∀k∈V

(8)

yik∈{0,1},∀i∈H,∀k∈V

(9)

其中，设定仅当客户i由车辆k配送时，yik=1，否则yik=0，仅当车辆k从客户i到客户j时，xijk=1，否则xijk=0。

在该模型中，式(1)为目标函数，为单目标问题，仅要求Z(车辆的总行驶距离)最小，式(2)限制了车辆的承载能力(车辆单次运输的货物不能超过其承载能力)，式(3)限制了每个客户点仅能到达一次，式(4)限制了每个客户点都必需要到达，式(5)限制了要从每个客户点驶离(不能停留在客户点)，式(6)限制了车辆线路从配送中心出发，最后要回到配送中心。式(7)限制了车辆到达客户点的时间范围。式(8)和式(9)限制了描述时间的变量xijk和yik的取值只能为0或1，以表示车辆k是否从客户点i到客户点j和车辆k是否经过客户点i的客观事实。

三、基本蝙蝠算法

Yang[8]受到蝙蝠在高维空间定位、捕猎方式的启发，于2010年提出了蝙蝠算法(Bat Algorithm，BA)，其可以应用于各种实际问题的求解。

蝙蝠算法基于以下原则[8]：

(1)每只蝙蝠在捕食过程中，都是使用回声定位的方法来判断自己和猎物或障碍物之间的距离(而不是使用视觉或嗅觉)。

(2)每只蝙蝠在位置xi处，以速度vi按任意方向飞行，并发出不同频率fi和响度Ai的超声波来搜索猎物。蝙蝠会根据它们离猎物的距离来调整超声波的响度Ai和脉冲发射频率ri。

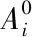
蝙蝠算法的实现步骤如下：

Step2：根据每只蝙蝠的初始位置xi和适应度函数f(x)，得到每只蝙蝠的初始目标值，通过比对，得到当前全局最优解x*。

Step3：根据式(10)、(11)、(12)进行迭代，更新下一代各蝙蝠的位置、飞行速度和超声波频率。其中β为[0,1]上的随机数。

fi=fmin+(fmax-fmin)β

(10)

(11)

(12)

(13)

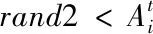
(14)

(15)

Step6：计算出当前所有蝙蝠的适应度值，并筛选出当前的全局最优解。

Step7：重复执行Step3-Step6，直到满足精度要求或达到设定的迭代次数。

Step8：输出全局最优解。

基本蝙蝠算法由于其模型简单，在应用的过程中，容易陷入局部极值，无法得到全局最优解；其又容易在后期出现收敛速度慢等问题，对其应用带来了极大的不便。因此，对蝙蝠算法的改进也从未停止过，如文献[5]中，马祥丽将蝙蝠的位置x对应了两个向量：xa和xb，其中一个表示车辆的编号，一个表示配送的顺序，其相当于省去了两个限制条件(3)、(4)式(每个客户点只能到达一次，每个客户点都要送到)，其增加了维数，但却也减少了计算过程，最后的仿真结果也验证了其有效性。文献[6]中，戚远航在蝙蝠算法中引入了随机插入策略、普通插入搜索、交换搜索等，提高了搜索空间，加强了蝙蝠算法的收敛效率。

四、改进蝙蝠算法解决VRPTW问题

因为基本蝙蝠算法是被设计用来解决连续函数的优化问题的，而VRP的解是离散化的(若干个客户点的有序序列)，所以要想用蝙蝠算法来解决VRP问题，首先要将VRP问题中的各变量进行编码，然后再制定BA算法在VRP问题中的相关运算规则及相关操作算子。

(一)编码和解码

设有L个客户点，K辆车，蝙蝠种群规模为s，维数d=L+K-1，记蝙蝠种群集合S={1,2，…，s}，编码长度集合D={1,2，…，d}。将蝙蝠位置xi(i∈S)取为(1,2，…，d)的一个全排列。解码时，首先在xi的首末位置各插入一个0，以表示车辆从配送中心出发，最后回到配送中心，再将xi中大于L的分量换为0，以代表配送中心，于是xi就变为了各个车辆的配送路线了。例如L=10，K=3，假设最优解x*为(1,4,6,8,11,2,3,5,12,7,9,10)，解码时，x*变为(0,1,4,6,8,0,2,3,5,0,7,9,10,0)，于是三辆车的线路就为0-1-4-6-8-0,、0-2-3-5-0和0-7-9-10-0了。

(二)操作算子

因为在蝙蝠的位置、飞行速度和超声波频率的更新公式中，存在位置、速度和频率的加法、减法或乘积运算，所以需要定义其相关的操作算子，定义如下所示：

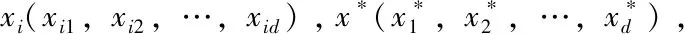
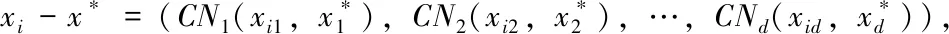
x+v为x先按CN1交换，其结果再按CN2交换，一直到按CNd交换之后的结果。

v1+v2，表示每一次有两个交换数，同时交换两次。但是由式(2)可以看出v2f可能不是整数或超出了配送点的编号范围，需要进行修正操作，采用向上取整，数值超过范围的取临界值或取一个在范围内的随机值或取当前全局最优解在此处的分量。本文f取在[0,1]上，然后采取向上取整。

(三)精英保留策略

在局部搜索中，如果找到了比全局最优解更优的解，更新当前全局最优解，同时群体中适应度最差的个体替换成之前的全局最优解，以提高收敛效率、避免丢失潜在的良好精英片段。

图1 算法流程图

五、仿真实验

本文算法的相关实验均在同一实验环境中进行，其中CPU主频为2.50GHz，内存为12GB，操作系统为64位windows 10，编程语言为C++。

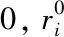
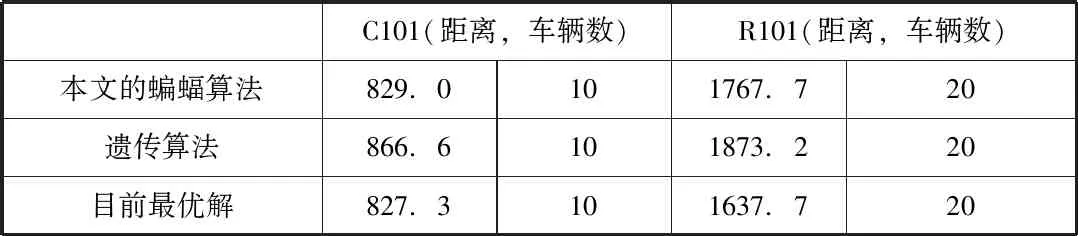
表1 本文的蝙蝠算法与多目标算法的比较结果

本文得到的最优的一次路径为：

C101中车辆1线路0-57-55-54-53-56-58-60-59-0，车辆2线路0-98-96-95-94-92-93-97-100-99-0，车辆3线路0-81-78-76-71-70-73-77-79-80-0，车辆4线路0-67-65-63-62-74-72-61-64-68-66-69-0，车辆5线路0-20-24-25-27-29-30-28-26-23-22-21-0，车辆6线路0-43-42-41-40-44-46-45-48-51-50-52-49-47-0，车辆7线路0-90-87-86-83-82-84-85-88-89-91-0，车辆8线路0-5-3-7-8-10-11-9-6-4-2-1-75-0，车辆9线路0-32-33-31-35-37-38-39-36-34-0，车辆10线路0-13-17-18-19-15-16-14-12-0，总距离为828.936768。

从结果来看，虽然差不多，但是遗传算法的迭代次数、群数数更多，也就意味着计算更复杂，耗时更多。

六、结论

本文提出了一种改进的蝙蝠算法求解VRPTW问题。实验结果表明蝙蝠算法具有较强的寻优能力、较高的鲁棒性、较少的时间耗费；但蝙蝠算法的改进工作仍有不少的前进空间，还需要更多的研究与改进。