砂带抛光机器人力/位混合主动柔顺控制研究

秦振江，赵吉宾，李 论，张洪瑶

（1.东北大学 机械工程与自动化学院，沈阳 110819；2.中国科学院沈阳自动化研究所中国科学院机器人与智能制造创新研究院，沈阳 110016）

0 引言

随着加工制造业对零部件的表面精度要求越来越高，抛光工艺越来越多的成为零件加工的最后一道工序，目前研磨抛光加工主要还是依赖于工人手工操作，然而手工操作难以保证恒力作用于工件，导致工件表面一致性较差，同时手工抛光还有效率低，工作环境恶劣等缺点[1]。机器人技术的发展为解决上述问题提供了方案，机械手臂动作灵活，在加工的过程中可以随时调整姿态，这为机器人加工过程中恒力控制提供了基础。

经典机器人柔顺控制主要是基于机器人动力学的阻抗控制和力/位置混合控制两大策略，但由于机器人动力学建模复杂，模型参数不确定及接触环境不确定等因素，使得其难以推广应用[2]。针对目前广泛使用的工业机器人，结合六维力传感器，提出运用最小二乘系统辨识实验法建立力/位置混合控制力控模型，避免了建立机器人加工过程中动力学模型的复杂性，并基于模糊PID的过程控制，搭建砂带抛光机器人恒力控制系统，完成加工过程中的恒力控制。

1 砂带抛光机器人系统组成

砂带抛光机器人系统组成，如图1所示。将KUKA机器人与砂带机结合构成加工系统，结合六维力传感器完成机器人加工柔顺控制。

图1 砂带抛光机器人系统

上位机通过以太网分别于机器人控制柜、六维力传感器相连，六维力传感器安装于机器人末端法兰与被抛光工件之间，可以测量力传感器坐标系下X、Y、Z三个方向的力与力矩。在机器人抛光过程中，通过TCP/UDP通信协议，将上位机与机器人、力传感器通信连接，力传感器实时采集加工过程中受到的作用力，并将所采集的力信息传输到上位机，上位机计算工件所受抛光力大小，对比抛光力和参考力的大小，通过恒力控制算法计算机器人位姿调节量并传输到机器人控制系统，调节机器人运动，实现对抛光力的实时补偿功能，从而使整个抛光过程保持在相对恒定作用力范围之内。

力/位置混合柔顺控制策略是指将机器人运动空间在笛卡尔坐标系下分解，自由方向上的运动用位置控制器进行控制，受限方向上的运动用力控制器进行控制，两组控制器的控制量之和为关节控制量[3]。本文基于力/位置混合主动柔顺控制策略就是在实际加工过程中，对加工轨迹由轨迹程序进行位置控制，对加工轨迹的法向方向进行力控制，两者控制量共同作用于机器人位姿控制系统，使得机器人在抛光过程中保持在一个相对恒定的作用力范围之内。

2 抛光工件重力补偿与受力分析

2.1 抛光工件的重力补偿

机器人在抛光过程中姿态会随着加工轨迹发生变化，使得工件重力G在力传感器坐标系上分量发生变化。为了消除工件重力对求解接触力的干扰，影响恒力控制，必须对工件进行重力补偿。

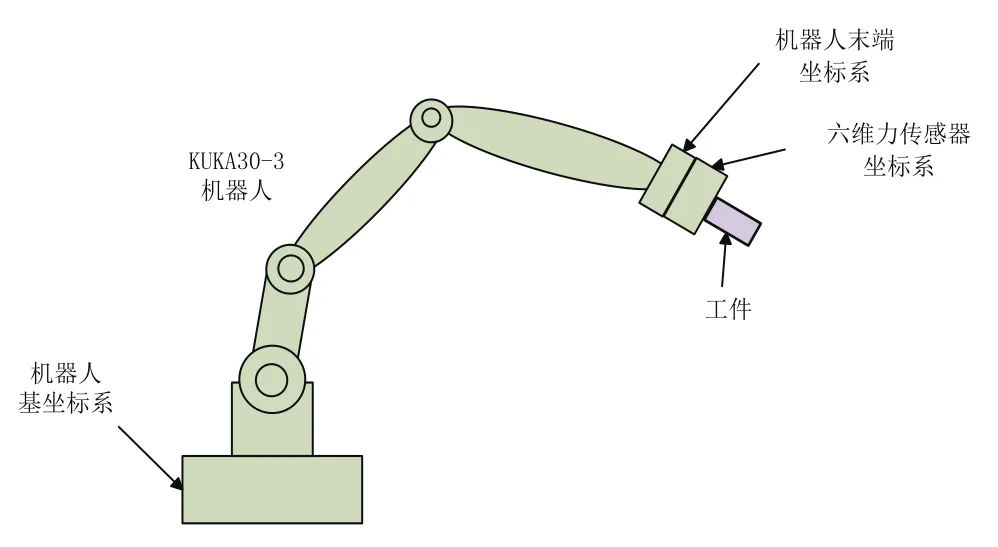
图2 机器人坐标系位置

机器人抛光系统中涉及到三个坐标系，如图2所示，机器人基坐标系BASE、机器人末端坐标系END、力传感器坐标系SENSOR。工件重力在基坐标系中的值为BFG=[0 0 -G]，为常数；力传感器直接感受到负载重力作用力的大小为：SFG=[FGXFGYFGZ]。根据机器人坐标变换，则有如下等式：

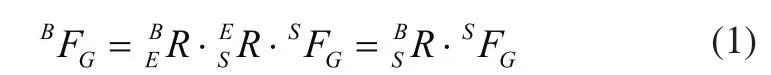
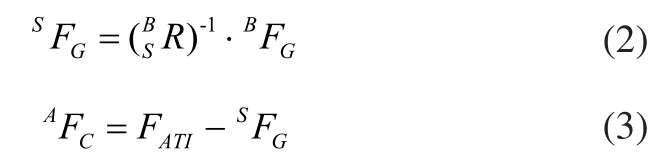
2.2 抛光工件的受力分析

抛光工件受力模型，如图3所示，其中α为砂带与水平的夹角，θ为砂带接触面与工件之间的夹角，力传感器受到来自工件法向的压力Fn，抛光夹具和工件自身的重力G，以及工件与砂带接触产生的摩擦力f。

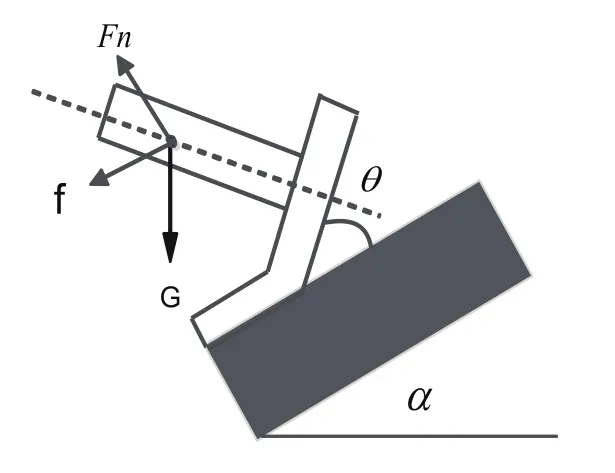
图3 工件受力模型

在抛光过程中，通过重力补偿算法将重力对六维力传感器进行力补偿，忽略加工过程中的惯性力影响，这样力传感器相当于只受接触力和摩擦力作用。由于抛光过程中，机器人的位姿在不断的变化，为了求解抛光接触力，即工件受到的法向压力Fn，需要将重力补偿后力传感器的力转换到机器人基坐标系下。定义接触力Fn在基坐标系中的单位向量为：e=(e1, e2, e3)，则接触力为：

3 恒力抛光控制算法

抛光机器人恒力控制算法流程如图4所示，其中Fr为按照工艺要求给定的抛光力，Fn为上位机计算的抛光接触力值，比较Fr与Fn，通过力控模型求解得到位置修正量ΔX对加工轨迹进行修正，实现基于机器人力/位置混合主动柔顺控制的恒力控制算法。

3.1 基于最小二乘的力控模型求解

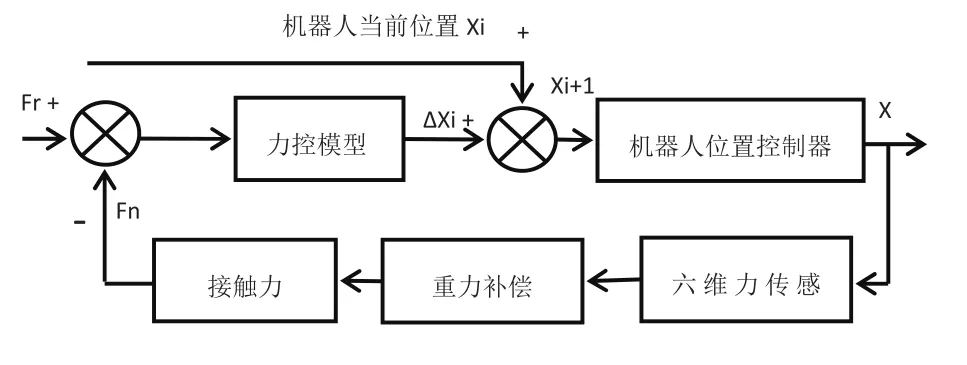
图4 力/位置混合控制流程

基于最小二乘法，对实验过程中获取的抛光接触力和与之对应的机器人位置数据进行辨识，求解抛光力与机器人末端执行器位置的具体函数关系。这样在恒力控制中可根据给定的抛光力与实际接触力的差值，计算机器人位置调节量。机器人夹取工件进行砂带抛光时，将机器人及末端执行器等效为刚体，其受力模型可以等效为弹簧加阻尼的二阶系统，实验中获得的3000个接触力与位置数据分布如图5所示。

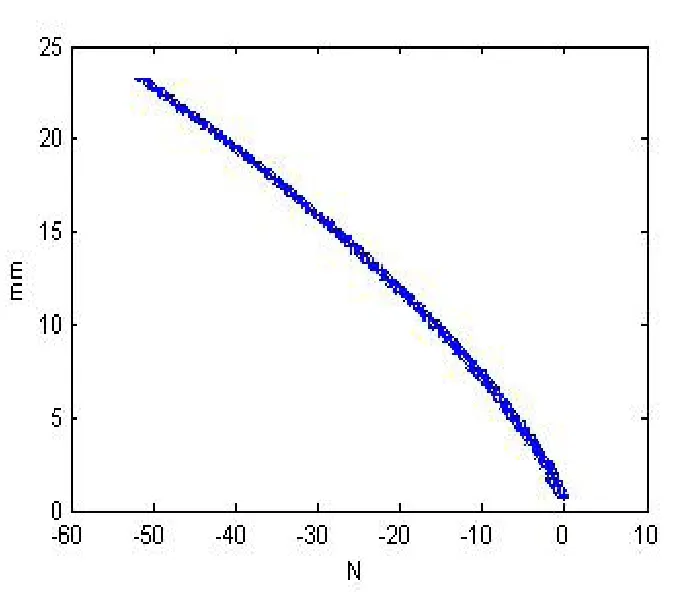
图5 数据样本图

对于二阶系统，结合图5的数据样本分布，建立公式(5)所示的力控模型，需要辨识的参数就是a，b，c。

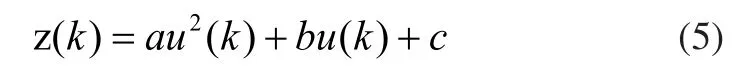
式(5)中，z(k)为系统输出量的第k次真值，即机器人末端执行器位置变化量，u(k)为系统的第k次输入真值，即工件所受抛光接触力。

则式(5)可改写为：z(k)=h(k)θ，式中，θ为带估计参数。令k=1, 2, …, m，则有：矩阵表达式为：Zm=Hmθ，最小二乘法就是寻找一个θ的估计值θe，使得各次测量值的Zi（i=1, 2, …, m）与估计值确定的估计值之差的平方和最小[6,7]，即：

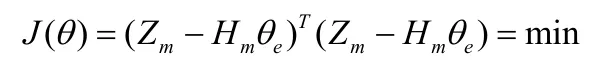
由上可求出系统的最小二乘估计值：

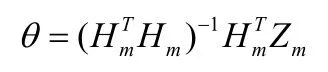
3.2 基于模糊自整定PID的过程控制

选用工业过程控制中广泛使用的PID控制器优化机器人加工柔顺控制过程。PID控制的特点就是对控制器参数，比例系数Kp、积分系数Ki和微分系数Kd进行调整，根据设定目标值与实际输出值的控制偏差，将偏差的比例，积分和微分通过线性组合构成控制量，对受控对象进行控制[8]。

机器人对工件进行抛光时，由于系统控制模型不可避免存在一定的误差，且工作环境复杂，非线性特性突出，典型的PID只利用一组固定的参数进行控制已经不能满足恒力抛光的控制要求。为此，采用如图6所示的模糊自整定PID控制器，利用模糊控制规则在线整定PID参数，以适应复杂的加工环境。

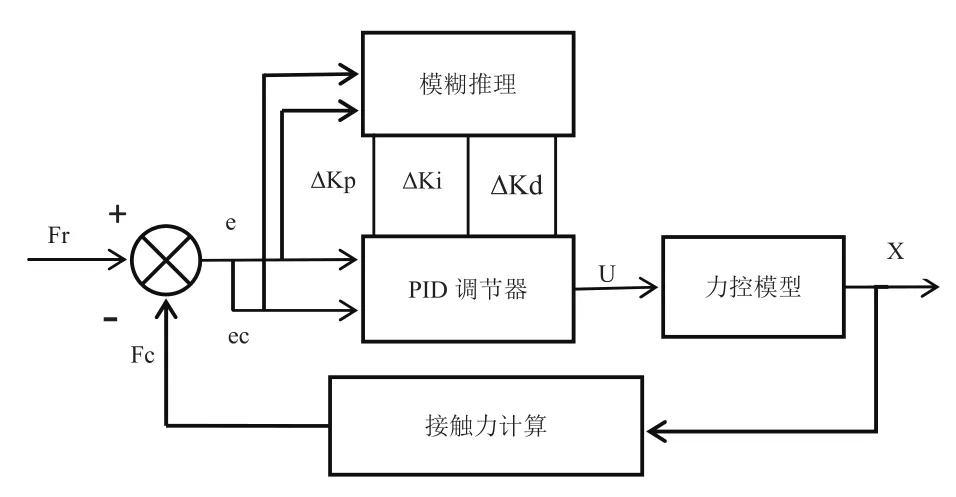
图6 模糊PID控制器结构图

图6中，Fr和X分别为恒力控制控制系统的输入和输出，输入为理想抛光力，输出为机器人位置调整量；e和ec分别为设定抛光力和实际抛光力的误差和误差变化量，作为模糊控制器的输入语言变量；ΔKp、ΔKi、ΔKd分别为模糊控制输出用于调整PID控制器参数[9]。定义它们的模糊论域为式(6)、式(7)，模糊集合为式(8)，考虑上位机程序书写，选用相对简单的三角形隶属函数作为模糊控制的隶属函数，建立ΔKp、ΔKi、ΔKd的模糊规则如表1所示，选用加权平均判决法进行非模糊化处理。

4 试验与结果

通过重力补偿算法，调节机器人在不同的位姿下，测得抛光工件重力在传感器坐标系的分量为GetFx，GetFy，GetFz以及通过重力补偿算法补偿后传感器值Fex，Fey，Fez如图7所示。补偿后的传感器值基本维持在0值附近，验证了重力补偿的有效性。

在重力补偿的基础上，通过示教机器人抛光轨迹，获取抛光路径中抛光力（0～50N）与机器人位姿变化量的对应数据。利用最小二乘法对获得的数据进行MATLAB线下辨识，实验过程如图8所示。通过处理实验过程采集的3000个数据点，得到辨识结果和辨识误差分别如图9、图10所示。对比图5和图9，结合辨识误差主要分布在区间[-0.6，0.6]mm内，验证了辨识结果的有效性。求得力控模型为：

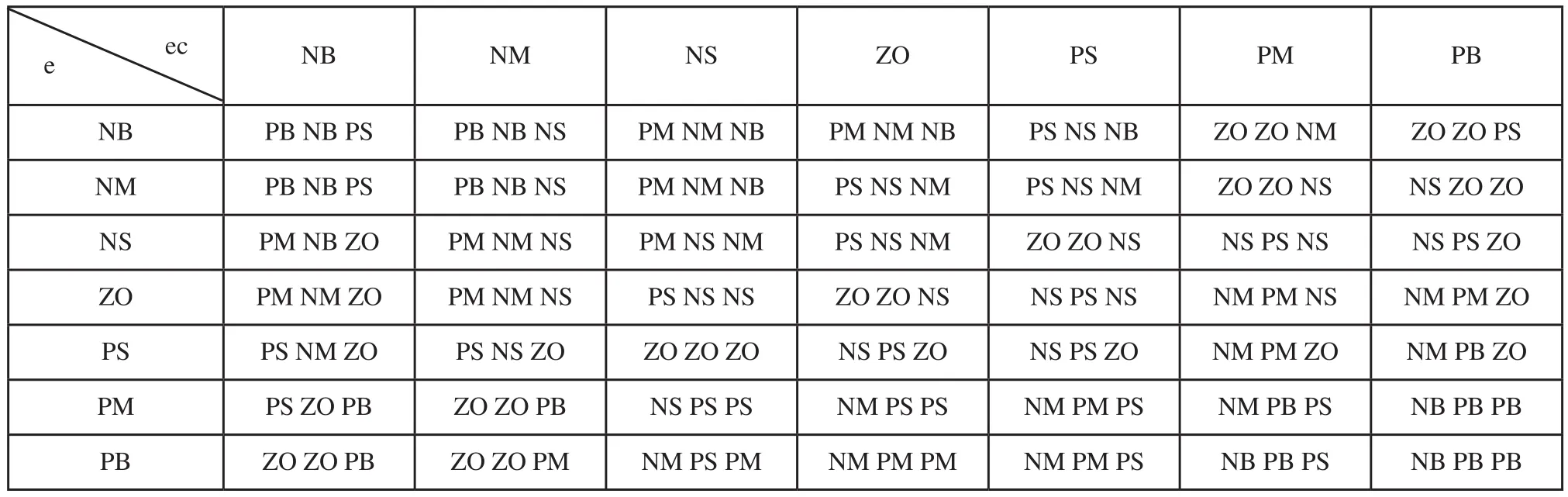
表1 模糊规则表

图7 重力补偿结果

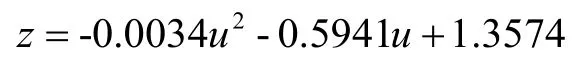
图8 卫浴五金件抛光加工

实验中将最小二乘方法得出的力控模型与模糊PID过程控制器结合，选择恒力控制的参考力为-10N（控制显示取其负值），砂带机驱动轮直径为50mm，转速为450r/min，砂带型号为100μm，PID的初始值分别为0.4，0.6，0.6，e和ec的实际论域分别设为[-30，30]，[-20，20]。模糊控制的力控效果，如图11所示，在力控稳定之后，误差波动主要分布在[-1，1]N范围内，实现了有效恒力磨抛控制。

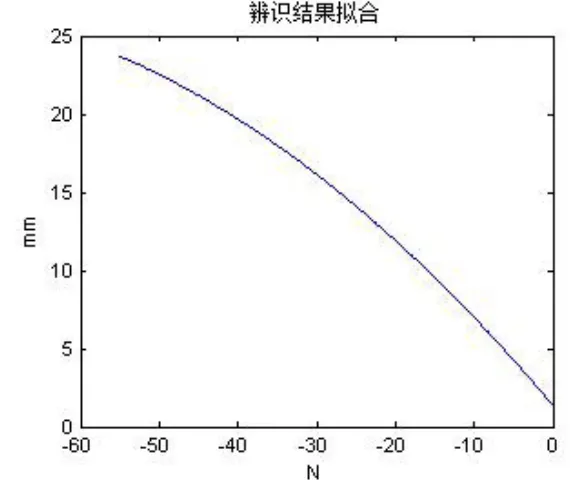
图9 系统辨识结果

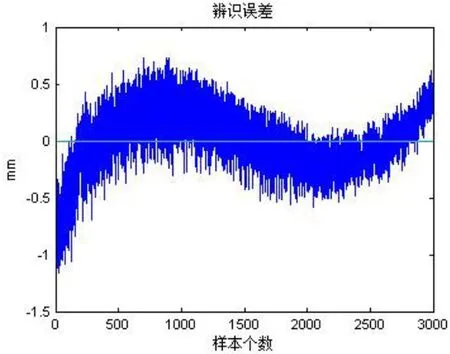
图10 系统辨识误差

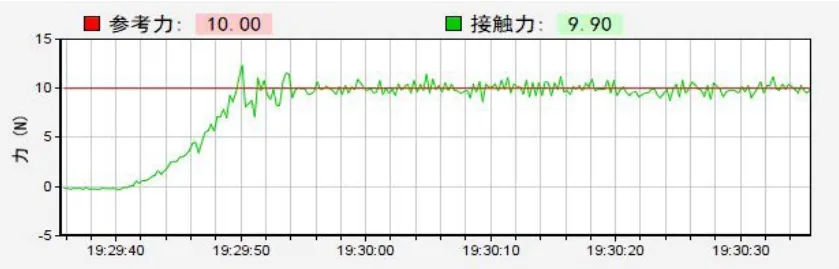
图11 恒力控制图

5 结论

在砂带机器人抛光系统中，通过对加工工件所受作用力进行分析，利用重力补偿算法，消除重力对求解抛光接触力的干扰。利用最小二乘方法辨识实验数据建立力控模型，结合模糊PID过程控制，搭建力/位置混合主动柔顺控制策略。通过对卫浴五金件进行抛光实验，结果表明，该控制策略能够将抛光作用力控制在相对稳定的范围内，实现恒力控制。