基于改进灰狼算法求解柔性车间调度问题

吴继浩，杨 涛

（西南科技大学 信息工程学院，绵阳 621010）

0 引言

柔性车间作业调度（Flexible Jobshop Scheduling Problem，简称FJSP），属于一个典型的NP难问题。解决作业车间调度问题的方法主要有以下四类：1）运筹学方法，包括整数规划，分支定界方法等；2）启发式规则；3）神经网络方法；4）元启发式算法。有很多知名的智能优化算法都已经成功应用FJSP领域，如蚁群算法、遗传算法、模拟退火算法和粒子群算法等。由NFL[1]定理可知，这个定理在逻辑上证明了没有哪种元启发式最适合解决所有的优化问题。这个领域每年都会提出新的元启发式算法。针对连续函数优化问题，Mirjalili等[2]在2014年模仿了一群狼的生活和捕食方式的行为提出了一种新的启发式算法，即灰狼算法（GWO）。

GWO是一种基于群体的元启发式算法，它设定每个狼群都有层次结构，狼群中的每只狼都有特定的角色。Mirjalili在文献[2]中，通过对29个连续函数优化问题的测试，结果表明GWO在求解精度和稳定性上要明显优于PSO、DE和GSA等算法。GWO中所有候选狼（解决方案）都被最好的三只狼所吸引，从而更快地聚集到这些好狼位置周围。但是这样也很容易造成GWO算法容易陷入局部收敛。由于上述原因，GWO的收敛性能有待提高。Zhang等[3]提出了基于Powell局部优化方法的PGWO算法，用于解决集群问题。龙文等[4]提出一种改进灰狼优化（IGWO）算法用于求解约束优化问题。

灰狼算法多用于解决连续函数问题的研究，在FJSP这类非常复杂的离散组合优化问题应用还比较少，本文针对经典的FJSP的特点，通过优化初始种群，采用新的解码机制，在迭代后期结合遗传算法的交叉变异和模拟退火的Metropolis准则提出一种新的“哨兵”机制，随机的向各个新的位置随机探索，有效的防止了GWO的局部收敛。经过实验对比，证实所提出的算法有效提高了GWO求解FJSP问题的能力。

1 问题建模及约束

对柔性车间（FJSP）问题[5]描述如下：车间中有M类设备，将一批订单分解为在一段时间内要求加工N个工件。每个工件由一系列工序组成，允许在一组可用的机器中加工它们。所有的作业和机器都在0时刻可用，而机器只能在给定的时间执行一个工序。不允许机器抢占加工。在本文中的FJSP问题设置机器的运行时间和运行时间之间的运输时间忽略不计。以最大完工时间最小为目标函数。

具体的建模和约束如文献[5]中Model M2，文献[5]中约束(2.1)定义了最大完工时间，约束(2.2)定义了工件的完工时间。如果没有Oij分配到机器M，约束(2.3)将M的起始和完成时间设置为零。约束(2.4)保证机器加工过程不能被打断且加工同一个操作时间相等。约束(2.7)保证了每道工序必须按照工艺顺序依次在指定的设备上加工，且必须在前一道工序i（如果存在）加工完成后才开始后工序j加工。约束(2.8)保证机器只能加工一个工件。

2 基本灰狼优化算法

Mirjalili在文献[2]中指出，GWO算法模拟了灰狼在自然界中的领导层次和狩猎机制。四种类型的灰狼，如alpha，beta，delta和omega，用于模拟领导层次结构。此外，还实施了狩猎、寻找猎物、环绕猎物和攻击猎物这三个主要步骤。算法进化过程中，alpha、beta和delta负责定位猎物的位置，并引导omega个体完成靠近、包围和攻击等行为，最终达到捕食猎物的目的。具体的过程及建模可以参阅文献[2]。

3 改进灰狼优化算法

3.1 编码及解码

对于GWO算法而言，如何将一个可行的工件加工序列转换为一个灰狼个体的位置向量是一个最为关键的问题。标准的GWO算法是主要是用于求解连续变量优化问题而提出的，FJSP是一个离散优化问题，如何设计有效的编码规则是问题解决的关键。文献[6]利用基于随机键编码的LOV规则，文献[7]采用了ROV规则。经笔者实际的多次实验仿真，得知LOV规则的编码更适用于灰狼算法解决FJSP问题。根据LOV规则设计如图1基于结构体的数据结构：

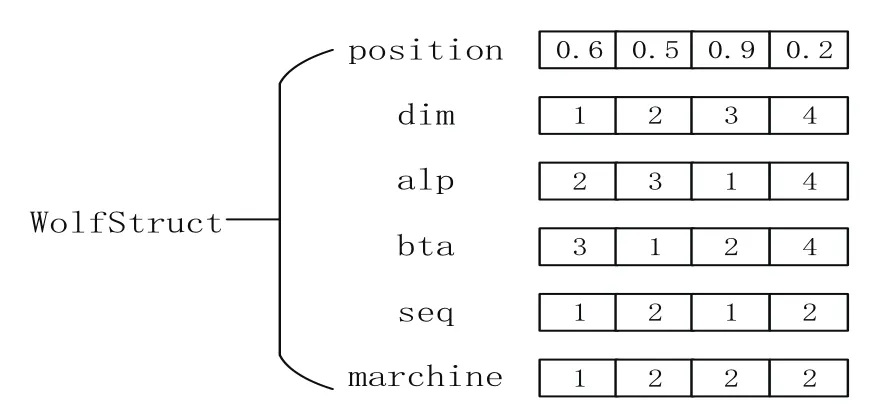
图1 灰狼个体数据结构

假设有两个工件，每个工件的工序数和可使用的机器如图2所示。

图2 工序图

编码时，首先随机生成WolStruct.poisition=[0.6，0.5，0.9，0.2]，根据LOV规则，对WolStruct.poisition变量做降序排列得到中间序列WolStruct.alp=[2，3，1，4]，然后按照公式获得加工顺序序列WolStruct.bta=[3，1，2，4]，其中φi为上述中间序列WolStruct.alp。最终得到加工序列WolStruct.seq=[1，2，1，2]。

经上述编码算法生成工序序列：C=[1，2，1，2]表示工件加工的顺序，第一个1表示工件1的第一道工序，第二个2表示工件1的第二道工序，转换成如T=[101，201，102，202]中间序列，解码安排机器，按照如下所示的步骤安排：

Step1：读入WolStruct.alp序列，解码得到T中间序列。

Step2：识别机器最早的停止时间Te及最后加工的工序Oi,j。

Step3：识别能够加工工序Oi,j+1:P(Oi,j+1)的所有可用机器。

Step4：计算每台机器的等待时间Mk∈P(Oi,j+1)：如果Mk在时间t没有加工任何工序，则等于Oi,j+1在机器Mk上的加工时间。如果Mk在t时刻正在处理工序Oz,y，则等待时间等于机器Mk等待操作的总处理时间+（Oz,y在Mk上剩余的加工时间）+Oi,j+1在Mk上加工时间。

Step5：选择等待时间最短的机器来处理Oi,j+1。如果Mk在时间t没有加工任何工序，则直接处理Oi,j+1，否则将Oi,j+1加入Mk的等待加工工序名单。

Step6：从Step2中得到Te及Oi,j，接着安排Oi,j+1到一个合适的机器。如果有很多等待名单，按照Cmax最小为规则选择一个加工序列。

3.2 种群初始化

初始狼群的好坏直接将决定后期狩猎过程的优劣，好的狼群将提高算法的运行效率。狼群G，个体S的位置可以表示如下：

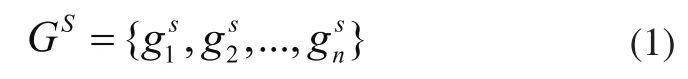
其中ub=100，lb=-100，W为群体G的灰狼总个数，n为工件工序的总个数，即灰狼的位置维度，这样每个位置分量取值范围在[-100,100]。

为了有效解决初始解的质量，保证初始化种群的多样性，提高初始解的质量。根据它们的处理工序差异性来定义两个位置之间的聚集性。随机生成后，经过LOV规则转换成加工序列WolStruct.bta。灰狼个体位置的聚集性由如下公式计算：

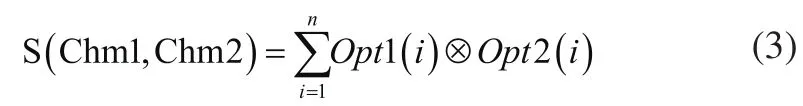
Chm1,Chm2是两个经过LOV规则转换后的工序加工序列WolStruct.bta。Opt1(i)，Opt2(i)和n代表WolStruct.bta的位置i上的值。当两个工序i位置上值相同时，操作返回0，如果不相等，则返回1。S的值被称为汉明距离，当S值非常小时，表示种群中两个灰狼的位置距离很近。定义聚集率：P=S/n。生成种群个体时，保证每个灰狼的位置PS＞Pcmax=0.5，可以有效保证生成狼群个体的多样性以提高解的质量。

3.3 个体位置更新方法

由于灰狼算法的设计原理，在GWO算法进化后期，群体中所有灰狼个体均向最好的三个灰狼个体区域靠近，从而导致了种群丧失了群体多样性，GWO容易出现早熟现象。文献[8]针对不同的应用领域都做出了一定有优化，有效地降低了GWO出现早熟现象和陷入局部最优的概率。本文提出“哨兵”机制。在种群中通过对最优灰狼个体进行GA算法的遗传变异操作，然后引入模拟退火算法Metropolis接收准则，生成种群的哨兵灰狼，在alpha，beta狼周围，不断的巡逻，降低狼群陷入局部最优解的概率。

初始化种群后，通过编码、解码操作，根据最大化完工时间得出每个灰狼的适应度，从小到大排序，最优的GN个灰狼个体保存为新的种群，并且确定alpha，beta，delta的值。

根据alpha，beta，delta结构体的seq序列，采用文献[9,10]的交叉、变异操作，得到3个哨兵灰狼。通过哨兵和alpha狼汉明距离来赋予其狼群等级，以确保哨兵狼的权限。根据3.2节定义的聚集率P，按照如下公式确定哨兵狼的合理性。当生成的哨兵狼聚集率PS∈{Pcmin，PC}就合格，否则一直重新交叉、变异直至合格。

式中：M为狼群最大迭代次数，m为当前迭代次数，PC为自适应聚集率，Pcmax为最大可接受聚集率，Pcmin为最小可接受聚集率。本文Pcmax=0.5，Pcmin=0.2。

采用Metropolis准则接收哨兵狼，在迭代后期替换种群中最差的3个灰狼个体。其中关键参数由如下公式确定：

初始温度：

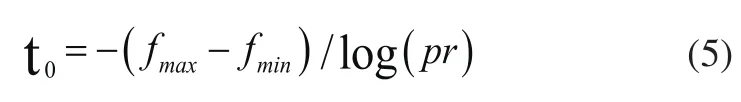
Metropolis准则：

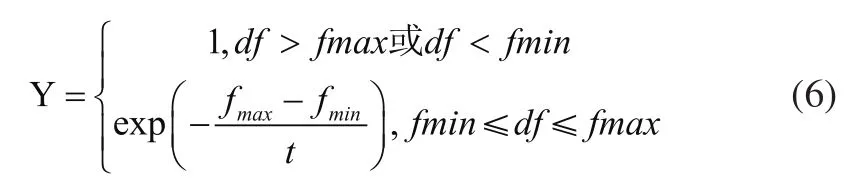
退温函数：

式中fmax和fmin分别为种群中最优和最差个体的适应度值。k为降温的次数，ω是一个常数。其中df为新产生个体适应度和要替换个体适应度的差，pr取值范围是(0,1)。

具体操作如下：

Step1：LOOPNew＞=LOOP*0.63时进入；

Step2：生成哨兵狼，计算适应度函数，如果df＞f max或df＜fmin就替换旧个体，否则按照（rand是介于0和1之间的随机数）概率接收新个体。

Step3：最差的第三个个体已经替换完毕，即保存当前种群进入下一次迭代。

本文将改进后的灰狼算法简称为GSGWO算法，流程图如图3所示。

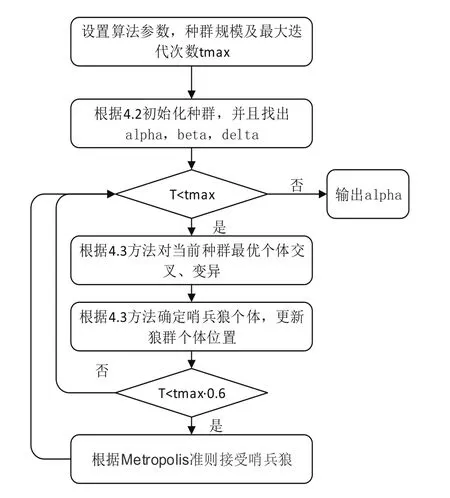
图3 算法流程图

4 仿真及实验

选择7个比较经典的测试集来验证提出的GSGWO算法，包括5个小规模Kacem实例[11]和2个大型的BRdata实例[12]。实例m×n，其中m是作业数，n是机器数。实验仿真环境为Windows10、处理器 Intel(R) Core(TM) i7-7700 CPU @ 3.60GHz、内存8.00G，MATLABR2016a实现算法编程。

为了验证改进GSGWO算法的寻优性能，与文献[6]中GWO+邻域局部搜索（HGWO），文献[8]中改进GA算法（GA），文献[9]中遗传算法+模拟退火算法（GASA），文献[2]中GWO，分别对上述7个实例进行求解，求解结果如表1，表2所示。GWO，HGWO，GA，GASA种群大小均取60，迭代次数均为5000次，其中GA，GASA交叉概率和变异概率为0.8、0.2，运行60次。

表1结果表明，在5个小规模Kacem实例问题，对于机器数较少的简单问题如4×5，8×8，GSGWO均可以给出比较满意的解，GWO，HGWO，GA，GASA，GSGWO均能找到最优解，对应8×8实例文中五种算法最优解甘特图如图4所示。当调度复杂度提高时，GWO寻找最优解的能力明显低于GA。表1中数据Δavg和m*的值可以看出，GWO算法虽然可以快速接最优解的周围，但是容易被头狼带到局部最优。GSGWO虽然从Δavg这个参数来对比，没有对GWO形成绝对优势，但是GSGWO由于有哨兵狼这个小分队，在后期接近最优解的范围，能够有一定的概率捕捉到最优解的位置。

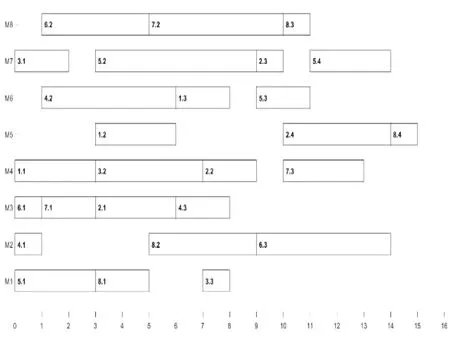
图4 8×8实例最优解的甘特图

通过表2结果表明，BRdata数据集中MK09为20×10，MK10为20×15。问题规模明显大于表1。对应20×15实例文中五种算法最优解甘特图如图5所示。GWO，HGWO算法都难以找到问题的最优解，寻优率都为0，但从Δavg这个参数可以得出，HGWO算法明显要优于GWO，更靠近最优解，HGWO加入的邻域搜索对算法陷入局部最优解有一定的抑制作用。标准GA算法的对FJSP问题的求解能力要优于标准GWO，GASA算法对FJSP问题的求解效率要高于GA算法，本文提出的GSGWO更容易找出最优值，虽然寻优率并不高，但是相对于标准的GWO和HGWO算法，GSGWO算法的优化性能已经有了很大的改善。GSGWO相对于GA，GASA表现出了对于解决FJSP问题的优势。

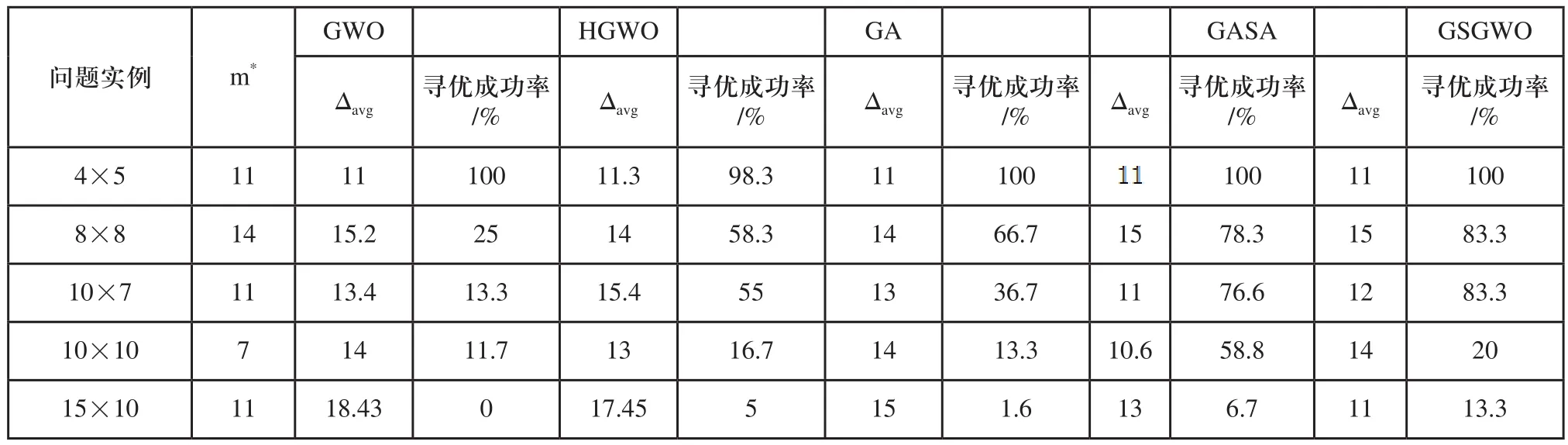
表1 Kacem实例的结果

表2 BRdata的结果

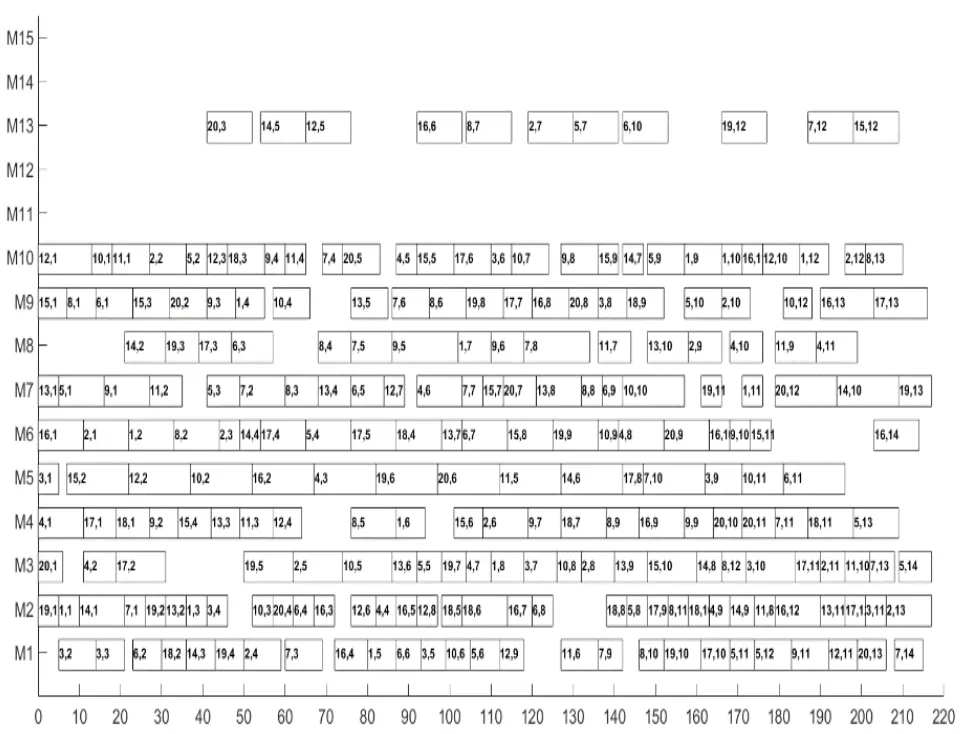
图5 20×15实例最优解的甘特图

5 结束语

本文针对的是单目标优化，FJSP问题大多都是多目标优化，工件优先级也未成考虑，滚动插单这些约束都未考虑，下一步研究工作方向，向着多目标，优先级，动态插单方向研究灰狼算法的有效性。车间调度问题还有很多分支，如流水车间、作业车间和开放式车间等。这些领域的灰狼优化算法的研究也是下一步的研究方向。