基于多场耦合的电机复杂工况暂态温度场研究

吴尧辉，董 雪，吴昊珍

（1.河南理工大学 电气工程与自动化学院，焦作 454000；2.直驱电梯－河南省工程技术研究中心，焦作 454000；3.郑州工商学院，郑州 450000）

0 引言

电机温度场的计算主要是考察电机实际工作的温升是否超过绝缘材料允许的极限温升。对电机温度场的研究多在稳定工况下进行[1～3]，采用公式法、热网络法和有限元法[4～6]，计算电机各部位温度，分析电机热源稳定时的温升规律。电机在实际工作中处于特殊的工作制或者工作环境下，热源是复杂多变的，当电机处于负载变化的复杂工况下，热源随负载的增加而增加，尤其是当电机处于过载状态时，考虑电机的热积累问题，由于绕组电流的增大导致铜耗的增大，电机温升迅速增加，长时间过载运行可能会使电机温升超过绝缘材料允许的极限温升。因此对负载变化的复杂工况下电机温度场的考核才能反映电机实际工作状况，为电机的使用和设计材料的选择提供依据。

由于负载变化的复杂工况下电机热源不稳定，温度场的计算应采用实时调取热源的方法计算，即温度场与电磁场进行实时耦合计算，通过建立温度场-电磁场的有限元多场耦合模型，计算复杂工况下电机暂态温度场。

1 多场模型的建立与模型参数设置

1.1 多场模型的建立

根据电机具体参数如表1所示，在满足精度要求的基础上建立二维电磁场和温度场模型，二维模型相比三维模型计算量较小，时间较短。电磁场和温度场模型如图1所示。

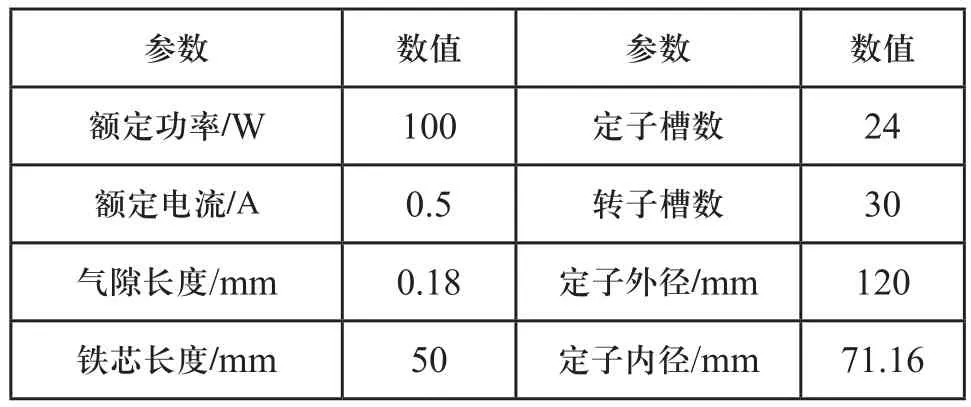
表1 电机主要参数

1.2 二维暂态温度场计算方程和边界条件

根据能量守恒，电机的发热量等于散热量加上自身的温升变化，即[7,8]：

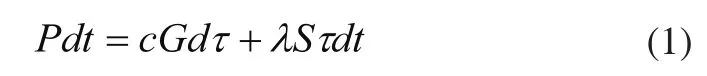
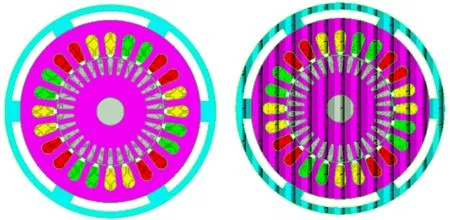
图1 电磁场和温度场模型图

式中，Pdt为单位时间dt电机产生的总热量；c为电机的比热容；G为电机重量；dτ为单位时间电机温升；λSτdt为单位时间dt电机总散热量；λ为散热系数；S为电机散热面积。

直角坐标系求解域内瞬态热传导方程和边界条件[9]：

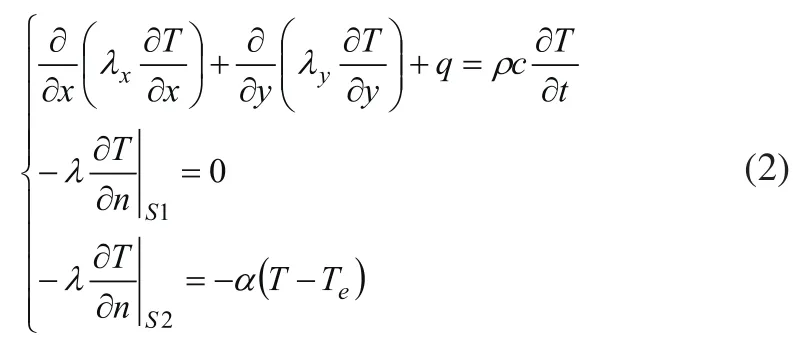
式中，λx、λy为物体在x、y方向上的导热系数；T为电机温度；q为热源密度；ρ为物质密度；c为物质比热容；t为时间；S1为电机绝热边界面；S2为电机散热边界面；n为边界法向量；λ为S1和S2面法向热传导系数；α为S2面散热系数；Te为周围介质温度。

1.3 模型参数的设置

1.3.1 材料性能参数的等效

相较于实际电机的三维结构，二维模型参数计算时应对电机端部进行等效计算。

1）对于定、转子端部绕组的等效，采用场路结合法等效为恒定阻抗[9]。

2）电机的温升与电机本身的重量有关，对于定子端部绕组和转子端环重量的等效通过折算铜和铝材料的密度折算到定、转子槽里。

1.3.2 热性能参数的等效

1）槽内材料导热参数的等效

定子槽内包含绕组、槽绝缘、槽楔、浸渍漆等材料，各个材料导热系数不同，为了简化计算，将定子槽部等效为一种材料的导热模型，等效导热系数λ的计算公式为[10]：

式中，kck为槽空率；kjq为浸漆系数；λjy为槽绝缘导热系数。

2）定转子对流系数的等效

对于定、转子气隙间复杂的热交换采用等效的热传导方式进行计算。定转子对流系数αeff包括气隙传热和端部传热两部分计算，即：

式中，α为气隙传热系数，可根据相关经验公式求得；α'为端部传热系数。

对于端部传热系数α、α'：

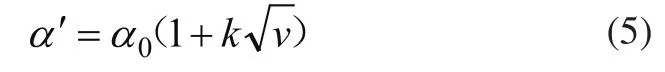
式中，α0为绕组端部、铁芯与空气的接触面的表面换热系数；k为吹拂效率系数；v为空气吹拂绕组端部、铁芯与空气接触面的速度。

3）外壳表面散热系数的等效

电机散热方式是自然散热，表面散热系数分外壳表面散热和端部散热两部分计算。

各表面散热系数可由经验公式求得，对于端部散热的散热系数通过折算到定子外表面与外壳之间的散热，端部的折算为：

式中，α1为电机实际表面各部分散热系数，S1为实体电机表面积，α2为二维模型等效对流散热系数，S2为定子外表面面积[2,7,8]。

2 电磁场-温度场耦合参数设置

2.1 多场耦合计算方法

图2 多场耦合模型求解过程

负载变化的复杂工况下，电机热源和热相关参数一直在变化，温度场需多次调取热源计算整个复杂工况。电磁场模型计算平均热源，温度场模型调取平均热源求解后产生温升，热相关参数改变，再次求解参数变化后的电磁场，产生平均热源后再赋给温度场，温度场在上一次求解基础上继续进行计算，如此往复，求解满足精度要求的暂态温度场。仿真计算过程如图2所示。

2.2 电磁场和温度场模型计算时长与步长

电磁场计算热源时，电机热源随负载一直在变，在保证精度基础上减少计算量，电磁场模型根据工况的不同设置1～2ms的步长计算各个负载下的热源。

温度场计算时，不同工况选用适当的步长计算。热源稳定时，温度场选用较大的步长计算；复杂工况下热源不稳定，温度场选用较小的步长计算，温度场步长至少比电磁场步长大一个数量级。各自模型的计算时间和步长如表3所示。

2.3 各复杂工况电磁场-温度场模型耦合参数

我国现行的国家标准规定电机工作制为S1～S10共10类，电机实际工作时，工作制不足以包括所有的复杂工况。针对小型异步机DJ16规划的复杂工况如表2所示。电机每个复杂工况均包含额定负载、1.3倍负载和1.5倍负载。

表2 不同复杂工况的负载变化

多场模型耦合时，耦合频率根据热源变化频率设置。负载变化频率较高时，热源变化较快，耦合频率较高；负载变化频率较低时，耦合频率较低。各工况耦合频率如表3所示。

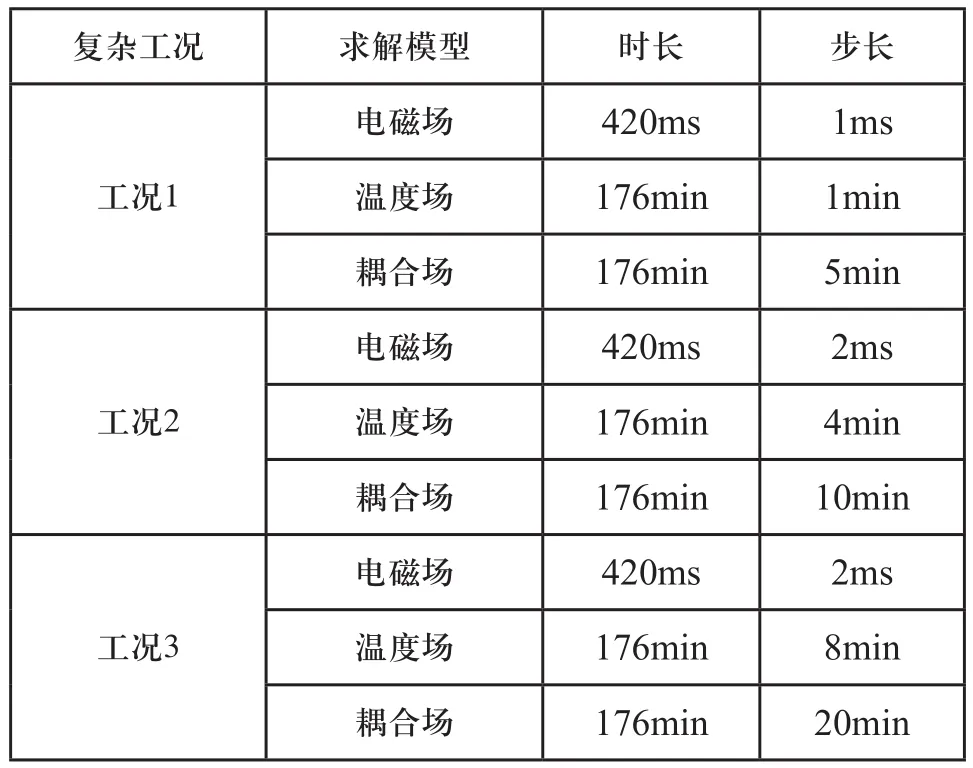
表3 各模型求解时长、步长和耦合频率

3 各复杂工况暂态温度场的计算及规律分析

3.1 工况1高频变化负载温度场的计算

环境温度为28℃，电机运行176min后的温度场部分仿真数据如表4所示。如图3所示是电机运行33min的温升曲线图，0～11min，定、转子和外壳温度持续上升。0～5min内定子槽内温度上升最快，定子槽内的热量一部分传递到外壳，一部分传递到转子，而转子的热量只能通过气隙向定子槽内传递，因此转子本身温度上升很快，5～10min转子与定子槽内温度基本相等，之后转子温度很快超过定子槽内。

电机定子槽内温度在1.3倍恒定负载与高频变化负载变化情况如图4所示。负载高频变化时，温升曲线跟随负载的变化一直处于震荡状态。额定负载时温升增加缓慢，1.3倍和1.5倍过载状态时，温升增加迅速，整体温升趋势与1.3倍恒定负载时趋势基本一致，1.3倍恒定负载定子温度高于高频变化负载3℃。在实际中为了简化计算，可用恒定负载的温度场计算来近似地代替负载高频变化的温度场计算。

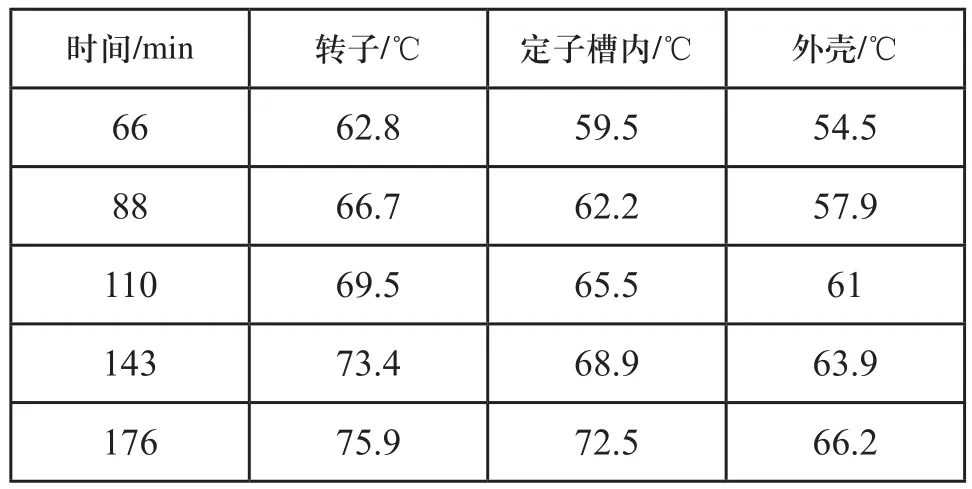
表4 工况1暂态过程温度场仿真数据

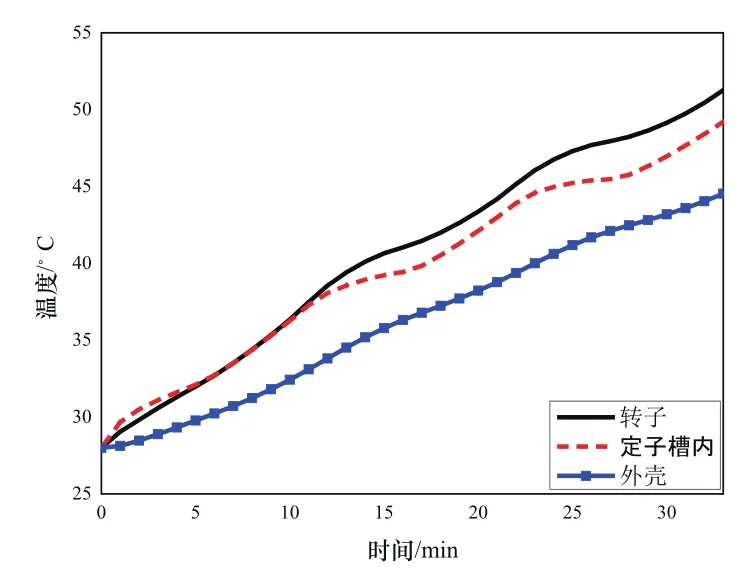
图3 工况1温升曲线图

3.2 工况2中频变化负载温度场的计算

环境温度为28℃，电机运行176min后部分时刻的温度场数据如表5所示，温升曲线图如图5所示。第一个周期内，电机整体温度呈上升状态，1.3倍负载和1.5倍负载时温升相比额定负载时增加迅速。第二个周期开始时，电机负载由1.5倍过载状态到额定负载状态，温升曲线趋势平缓。64～88min，随着负载的增大，温升曲线继续迅速上升。

图4 定子槽内温升对比图

第三个周期88～108min即额定负载开始后，电机定、转子温度稍有下降，外壳温度继续增加。由于前两个周期电机的热积累，定、转子温度均已超过电机额定负载运行时热平衡的温度，此时电机由1.5倍负载状态到额定负载状态时，电机热源减小即发热量减小，电机散热量增加，电机定、转子温度稍有下降，外壳温度继续增加。由额定负载到1.3倍过载状态后，电机整体温度继续上升。如此循环，电机最终运行176min后转子温度达到79℃，定子温度达到74.7℃，外壳温度达到68.2℃。

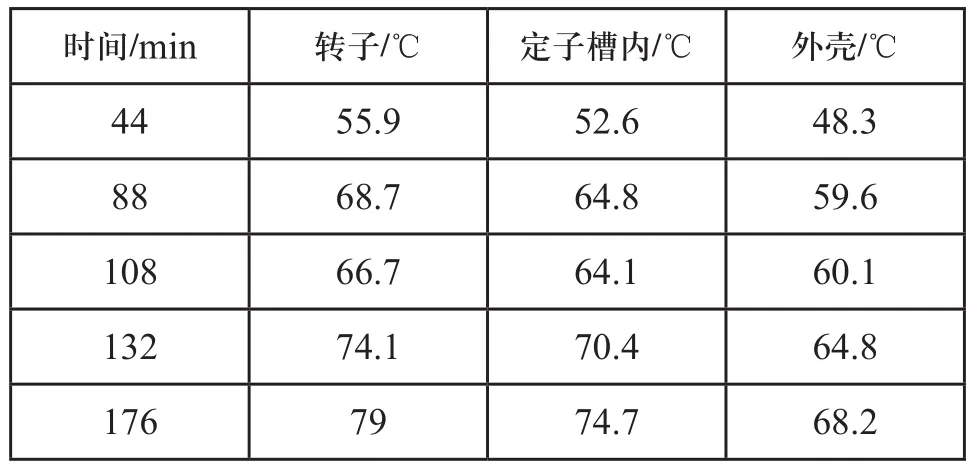
表5 工况2暂态过程温度场仿真数据

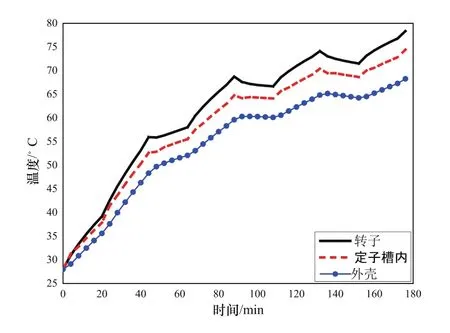
图5 工况2温升曲线图

3.3 工况3低频变化负载温度场的计算

环境温度为28℃，电机运行176min后数据如表6所示，温升曲线如图6所示。对比2、3两个工况，结合表5和表6，负载持续率相同，负载变化的频率不同时的温升情况分析：工况2、3中负载持续率相同，工况2负载变化的频率比工况3高，考虑电机热积累现象，整个运行时间结束后工况2的温度稍低于工况3，过载状态时间持续越长，电机温升越高，长期低倍过载运行对电机绝缘材料不利。

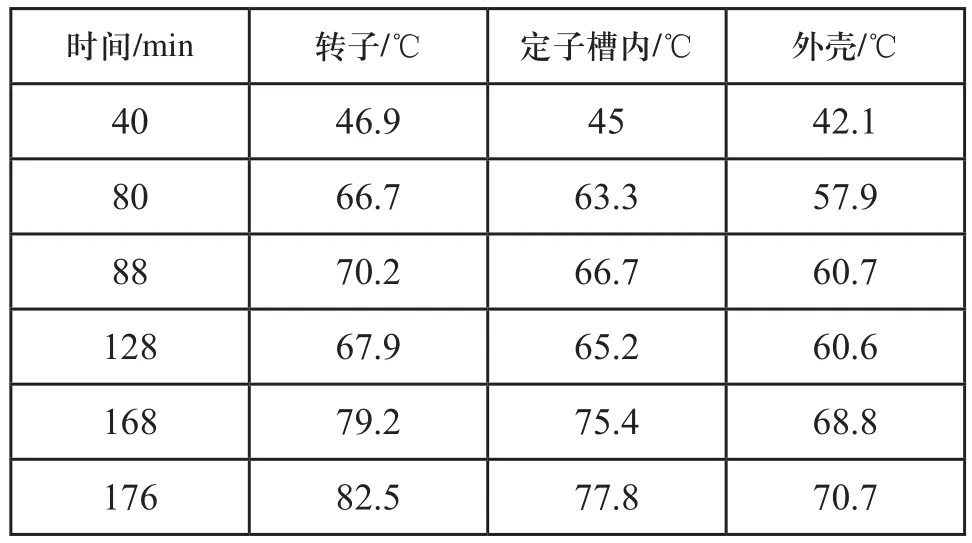
表6 工况3暂态过程温度场仿真数据

图6 工况3温升曲线图

4 实验研究与分析对比

4.1 实验平台的搭建

搭建负载变化的复杂工况下温度场实验平台进行电机暂态温度场实验。电机中埋设的温度传感器是K型热电偶，埋设位置如图7所示，1～20点用数据采集卡进行数据采集，转子采用红外测温仪进行数据采集。搭建的实验平台如图8所示。

4.2 各复杂工况仿真与实验结果对比分析

工况1运行176min后，转子实验温度是75.6℃，相比仿真温度75.9℃低0.3℃；定子槽内中实验温度是72℃，相比仿真温度72.5℃低0.5℃；外壳实验温度是65℃，相比仿真温度66.2℃低1.2℃。同样对比工况2、3运行176min后的实验与仿真数据，转子实验温度分别相较仿真温度低0.8℃和0.3℃，定子槽内温度分别相较仿真温度低0.7℃和1.3℃，外壳实验温度分别相较仿真温度低2.6℃和2.2℃，具体仿真与实验温度值如表7所示。

图7 电机传感器位置图

图8 实验平台图

由仿真数据与实验数据对比曲线图9可得到，各个复杂工况下的温度场实验数据曲线与仿真数据曲线趋势基本一致，温度分布一致，转子温度最高，其次是定子槽部，外壳温度最低。仿真数据曲线稍高于实验数据曲线。基于以上实验结果与仿真结果的对比，分析如下：

1）多场耦合模型是二维模型，仿真计算的参数对端部进行了等效计算，仿真结果反应的是电机z轴方向的平均温升，而实验所埋设的温度传感器只反应电机某一点的温度，因此仿真数据相比于实验数据较高。

2）电机内部埋设的温度传感器K型热电偶，是通过数据采集卡进行数据采集；转子通过红外测温仪进行数据采集，存在一定的测量和读数误差。

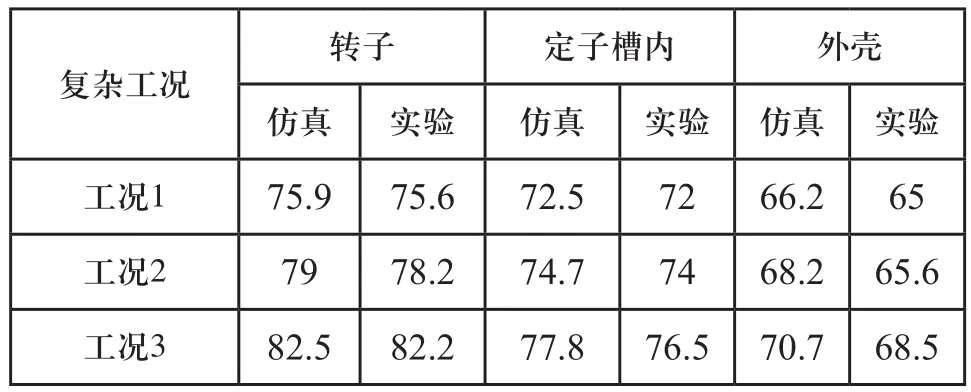
表7 各工况运行结束时刻各部位温度

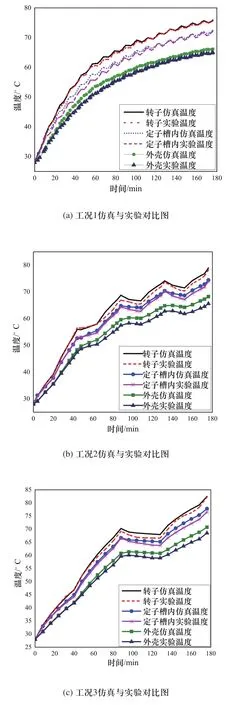
图9 不同工况仿真与实验对比图

5 结论

以小型封闭式异步电机为对象，采用多场耦合的方法计算复杂工况下的电机暂态温度场，分析不同工况下的温度分布和温升规律，通过与实验数据的对比分析，验证模型计算的正确性，得到以下结论：

1）复杂工况下电机的暂态温度场，采用多场耦合方法即电磁场和温度场实时耦合的方法计算电机暂态温度场。

2）多场耦合的计算模型要对材料性能参数和热性能参数进行等效计算。

3）电磁场-温度场耦合模型计算时，各模型采用合适的计算时长和步长，耦合模型采用合适的耦合参数。

4）合理的耦合热源进行等效计算能够简少多场耦合的计算量。