一种伺服系统两自由度复合控制器设计的新方法

刘红俐，朱其新，朱永红，张国平

（1.苏州科技大学 机械工程学院，苏州 215009；2.景德镇陶瓷大学机电工程学院，景德镇 333001；3.深圳市大族机器人有限公司，深圳 518058）

0 引言

伺服系统又称随动系统，是用来精确地跟随或复现某个过程的反馈控制系统。伺服系统使物体的位置、方位、状态等输出被控量能够跟随给定值的任意变化的自动控制系统。伺服系统最初用于国防军工，如火炮的控制，船舰、飞机的自动驾驶，导弹发射等，后来逐渐推广到国民经济的许多部门，如自动机床、无线跟踪控制等[1～3]。

在过去几十年中，伺服控制被国内学者进行了广泛的研究。文献[4]提出了一种交流永磁同步电机伺服系统的鲁棒控制器的设计方法，文献[5]提出了交流永磁同步电机伺服系统的非线性控制器的设计方法，文献[6]设计的交流永磁同步电机伺服系统的模糊自适应内模控制器的设计，文献[7]提出了应用于磁盘驱动的伺服系统的前馈解耦控制器的设计。但已发表的伺服控制文献大多讨论的是伺服系统的单自由度控制。

随着科学技术的不断发展，人们对控制系统的要求也越来越高，不仅要求控制系统有很高的跟随性能，而且要求控制系统有很强的抗干扰能力。在工业控制领域广泛应用的PID控制器等常规控制器，都只能设定一组控制器参数，属于一自由度控制器。一般来说，如果按干扰抑制特性最优来整定参数，则系统的跟随性能就会差；如果按跟随性能来整定参数，则干扰抑制特性就会不令人满意。所以常规控制器的设计通常采取折中或试凑的办法解决。这样一般能满足大多数控制系统的控制要求，但对高性能伺服控制系统而言则难以满足要求。为了解决常规控制器存在的问题，Horowitz在文献[8]中提出了两自由度控制器的思想。所谓两自由度控制是指采用适当的方法，找到两族独立的参数设计出两个独立的控制器，分别用来优化系统的跟随性能和干扰抑制特性。但两自由度控制在很长一段时间没有引起广大研究者的足够重视，直到1984年，在Horowitz的论文发表20年后，文献[9]才深入研究了两自由度PID控制器的优点，之后在两自由度PID控制器这一议题上又发表了较多论文[10]。

已发表的文献在讨论PID控制器的设计时，可分为两类：一类是PID参数的整定，PID参数整定的方法适用于对动静态性能要求不高的系统，但对高速高精度的伺服控制等场合，PID整定的方法不再适用；另一类是PID参数的优化设计，该类方法比较复杂，优化时间较长，而且不易被一般工程师所掌握[11]。针对现有PID控制器设计上的不足，本文提出一种基于极点配置的PID控制器设计的简便的方法。据作者所知，基于极点配置的两自由度控制器设计尚未见报道。受文献[8]和文献[9]的启发，本文将极点配置的PID控制器设计方法应用于两自由度伺服系统的控制器的设计中，详细讨论了前馈控制器和基于极点配置的PID反馈控制器的设计方法。

1 伺服系统位置环对象的数学模型

伺服系统通常包含三环结构，即电流环、速度环和位置环。要设计位置环的调节器，应将速度环用其闭环传函代替，但由文献[1]可知，按典型Ⅰ型系统设计电流控制器和按典Ⅱ系统来设计速度环控制器，则速度还的闭环传递函数为一高阶系统，此时位置控制器的设计十分复杂，所以应对其作降阶或简化处理。从工程上讲，可以应用反映位置环主要特征的环节来等效。

当位置环的截至频率远小于速度环的截至频率时，速度环的闭环传递函数可以等效为一个惯性环节[1,12]，即：

速度的积分是位置，所以位置环对象的数学模型为：

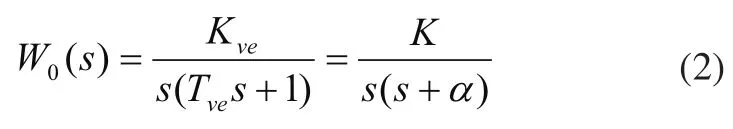
其中K=Kve/Tve，α=1/Tve，K为位置环对象增益，α为位置环对象的阻尼系数。

2 两自由度复合控制器的设计

2.1 不变性原理

两自由度复合控制的控制结构如图1所示，其中R(s)为系统给定，Y(s)为系统被控量，W0(s)为被控对象传函，Wc(s)为系统控制器传函，Wf(s)为前馈控制器传函，则系统的闭环传函为：

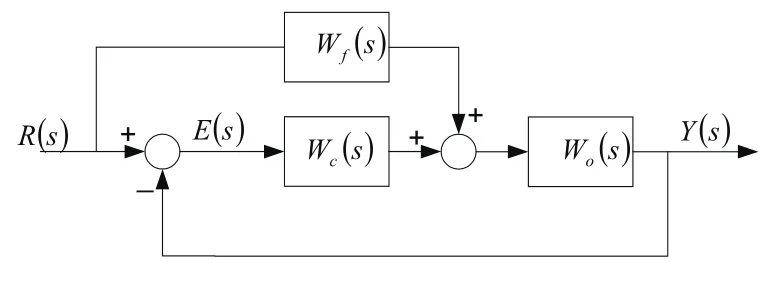
图1 复合控制的结构图

误差传函为：

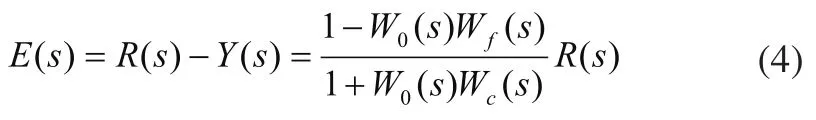
2.2 控制器的设计

由不变性原理设计前馈控制器，即：

1）在分析电流环时，速度环的反电动势被忽略，将电流环看成一个惯性环节只是一种近似。

2）实际的速度环的闭环传递函数是一高阶对象，将其看成一个一个惯性环节也是一种近似。

3）在位置伺服的被控对象中没有考虑伺服机械对象的共振模态。

所以要使伺服系统具有良好的动静态性能，必须要精心设计前馈控制器和PID反馈控制器，前馈控制器可以按不变性原理设计。PID反馈控制器可以由极点配置的方式设计，由式(1)可知，位置伺服系统的被控对象为，在实际的伺服系统设计中，K可由系统分析估算得到或由参数辨识精确得到，α也可由参数辨识精确得到，但在不进行参数辨识时α也可以根据经验直接取值，α一般情况下在10～50之间取值便可。

由式(5)可知，前馈控制器由两个纯微分环节组成，这在物理上难以实现。但在计算机控制系统中，可以在离散的状态下近似实现。

PID控制器的传递函数可表示：

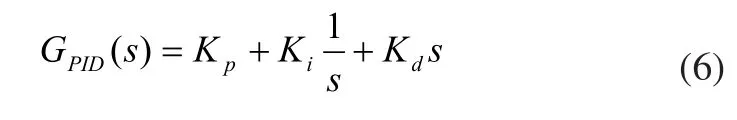
其中Kq，Ki，Kd分别为比例、积分和微分环节的系数。

在不包括前馈环节时，位置环的闭环传函为：

由于闭环传函的分母为3阶，所以闭环系统有3个极点，可以将这3个极点配置在如图2所示的位置上。

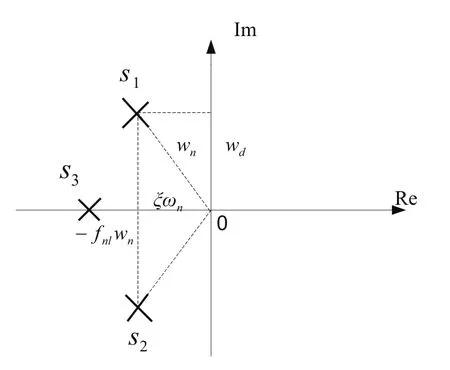
图2 系统期望极点的位置图

在图2中，s1和s2为一对共轭极点，s3为一负实极点且：

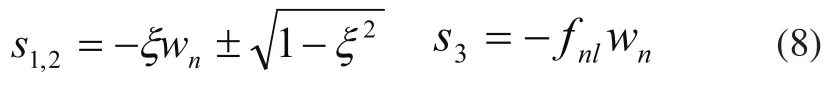
其中ξ为阻尼系数，wn为无阻尼振荡频率，fnl为第三极点比例系数。即将位置闭环传递函数的分母配置成，也即：

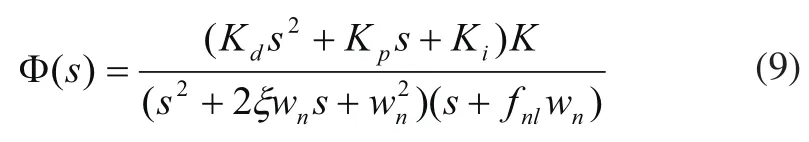
比较式(7)和式(9)可知：

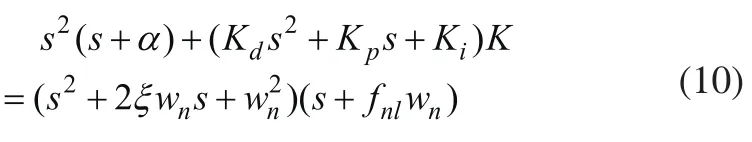
易得：

另外：

在设计PID控制器之前，应根据系统的动静态性能要求和传送部件的特性给出，wn取值越大，系统的响应越快，但太大会导致系统不稳定；为保证系统具有的足够的相角裕度，同时又具有较好的响应速度，ξ一般在0.6～0.8之间取值，常取0.707；fnl一般在1左右取值。这样由式(11)～式(15)便可计算出Kp，Ki，Kd，Ka和Kv。这样便完成了PID控制器和前馈控制器的设计。

3 实验

一个半导体生产装备中的伺服系统被用来验证本文的方法。实验中参数如下：系统的采样频率为2000Hz、伺服电机的极数是2、电机每一转的编码器的脉冲数为27200、编码器的精度为1μ m/count，K=3055，α=30，ωn=90π，ξ=0.707，fnl=0.5。在实验中用了S型加减速运动轨迹指令。伺服系统的位置跟踪响应曲线如图3所示，位置误差曲线如图4所示。由图3和图4可知，该复合控制器具有令人满意的动态和静态性能。

图3 伺服系统的位置跟踪曲线

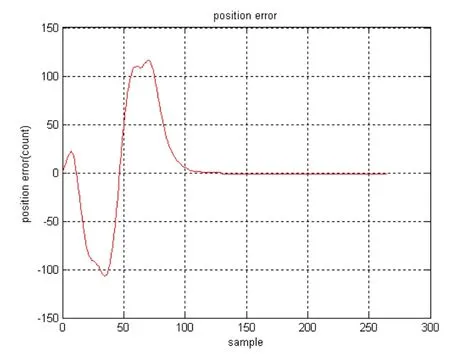
图4 伺服系统的位置误差曲线

4 结论

本文提出了一种两自由度控制器设计的新方法，前馈控制器通过不变性原理来设计，反馈控制器通过极点配置的方法来设计，并详细介绍了基于极点配置的PID控制器的设计方法，同时将该控制器应用于伺服系统的控制中。实验结果表明该两自由度复合控制器具有令人满意的动态和静态性能。本文只介绍了二阶对象的PID控制器的极点配置的设计方法，至于高阶对象的PID控制器的极点配置的设计方法有待于进一步研究。