基于一般灰数的灰靶决策模型拓展与应用
刘中侠,刘思峰,蒋诗泉
(1.南京航空航天大学 经济与管理学院,南京 210016;2.铜陵学院 财税与公共管理学院,安徽 铜陵 244000)
0 引言
灰靶理论最早是由灰色系统理论创始人邓聚龙教授提出,其基本思想是在决策模型中含有灰元或在一般决策模型与灰色模型相结合的情况下,从一组模式序列中,找出最靠近子命题目标值的数据,构造标准模式,各模式与标准模式一起构成灰靶,标准模式即是靶心。每个灰关联差异信息空间中的模式与靶心的灰关联度称靶心接近度,简称靶心度,并提出灰靶变换。继邓聚龙之后,刘思峰在灰靶决策模型中利用靶心距的数值反映了局势效果向量的优劣[1]。在邓聚龙和刘思峰已有的研究基础上,陆续有相关学者对灰靶决策进行深入研究和扩展[2-6]。文献[7,8]从决策者指标满意域和风险态度对群体决策的影响视角,提出了基于前景理论的三参数区间灰数群体灰靶决策模型,该方法充分考虑了专家关于各属性的心理期望灰靶和决策风险态度。文献[9]针对指标值为区间数的情形,把灰靶决策模型由实数序列推广到区间数序列,建立了基于区间数的灰靶决策模型。文献[10]通过比较指标集中各指标值与靶心连线所围成图形的面积大小来对决策方案的优劣进行评价,从而在一定程度上弱化了建模对象中极端指标值对靶心距计算结果的影响,建立了蛛网灰靶决策模型。文献[11,12]提出了冲突利益主体不完全确定权重信息情景下的群决策方法和基于区间数的多时点多属性灰靶决策模型,针对多属性决策的不确定性和多时点性,利用隶属度对案例进行排序,旨在对决策方案的排序进行优化。文献[13]结合层次分析法和离差最大法确定指标权重,提出了多指标灰靶决策的靶心贴近度法,该方法是对加权灰靶决策的一种改进。本文在已有的研究成果基础上,将灰靶决策理论从实数和区间灰数推广到一般灰数,针对一般灰数灰靶决策方法的不足,给出一般灰数的概念及其距离计算公式。运用多目标线性规划的理论给出确定指标权重的优化方法,依据灰靶决策思想,对目标属性值和方案值均是一般灰数的决策方案,构建了基于一般灰数的灰靶决策模型,在一定程度上拓展了灰靶决策理论。
1 一般灰数的基本概念
在现实问题中,由于多种原因会使得决策信息表现为复杂性和不确定性,为了准确地表示复杂不确定信息。在灰理论的思想的指导下,将区间灰数的概念和距离测度进行了拓展,这些研究将为灰关联与灰靶等决策模型提供了坚实的理论基础。
定义1[1]:设则称g±为一般灰数。其中任一区间灰数,满足且分别称为g±的下界和上界。
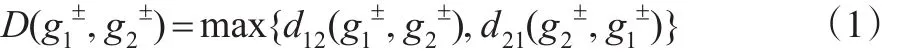
2 基于一般灰数的灰靶决策模型构建
基于一般灰数处理方法和灰靶决策模型的构建机理的角度,下面分别依次论述模型构建算法和步骤。
2.1 决策矩阵规范化处理
设skj为方案k的第j个指标值,该值为一个一般灰数,即,其中k=1,2,…,l;j=1,2,…,m。
(1)若skj为效益型指标,则规范化算子为,其中
(2)若skj为成本型指标,则规范化算子为,其中
2.2 靶心和靶心距的确定
2.3 计算投影一致性系数
定义5:称PrjA-A+(A-Ai)表示方案Ai与负靶心连线在正负靶心连线上的投影值;PrjAi+A(A-A+)表示正负靶心连线在方案Ai与正靶心连线上的投影值,其计算公式分别为
定理1:PrjA-A+(A-Ai)越大,方案Ai越靠近正靶心A+;越小,方案越远离正靶心越大,则方案Ai越靠近负靶心A-,PrjA+Ai(A-A+)越小,方案Ai越远离负靶心A-。
证明:(略)。
定理2:设PrjA-A+(A-Ai)与PrjAi+A(A-A+)如定义6所示,设,其中γi为一致性系数,则,且一致性系数γi越大说明第i方案越好。
证明:(略)。
定义6:称ψi=Ri--Ri+为靶心距得分函数。其中,Ri+表示第i个方案到正靶心的正靶心距,Ri-表示第i个方案到负靶心的负靶心距。其中,ψi值越大表明方案越优,值越小表明方案越劣。
定义7[14]:TODIM方案排序法,方案Ai相对每个方案Aj相对优势度,其中:
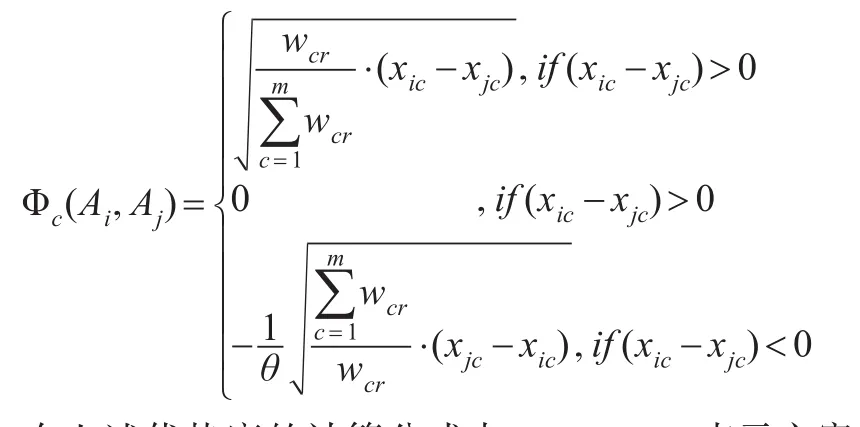
在上述优势度的计算公式中,Φc(Ai,Aj)表示方案Ai相对方案Aj在属性C下的优势度,参数θ是衰退系数,其值越小,表示决策者损失规避程度越高。最后计算方案Ai的全局优势度根据ξi的大小对方案进行排序,ξi越大,方案方案越好。
2.4 指标权重的确定
设指标权向量为w=(w1,w2,…,wm)T,根据灰靶决策模型的效果向量测度准则,建立以下权重确定的多目标最优化模型:
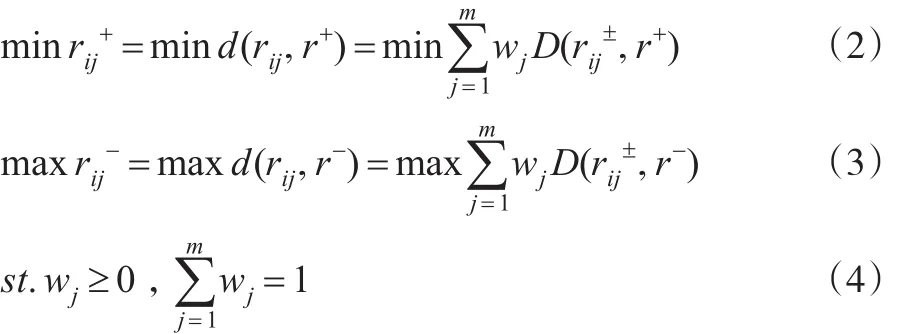
3 基于一般灰数的灰靶模型决策步骤
步骤1:决策信息规范化处理;
步骤2:正负靶心确定;
步骤3:依2.4确定权重,计算靶心距和靶心距得分函数;
步骤4:计算投影值;
步骤5:计算灰靶决策一致性系数γi;
步骤6:TODIM法计算方案全局优势度;
步骤7:方案排序。
4 案例分析
某投资银行准备对一个企业进行投资,通过第一轮筛选后,还剩最后三家企业,现要在这三家企业A1、A2、A3中选择一家,其评价指标分别为:S1表示企业年产值(千万元);S2表示企业社会效益(千万元);S3表示对环境污染程度,指标权重为W=(w1,w2,w3)经专家评价三个指标的权重范围为w1∈[0.1,0.2],w2∈[0.2,0.3],w3∈[0.3, 0.5],具体指标数据见表1。试确定银行的最佳投资方案。
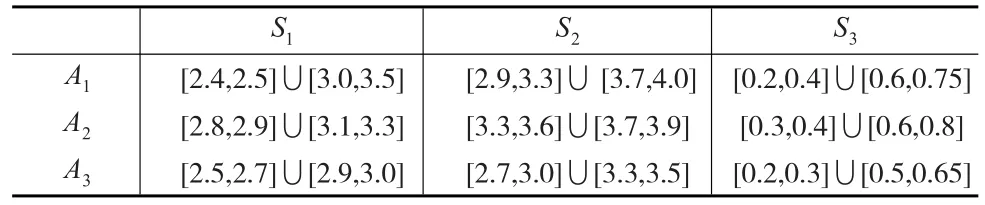
表1 决策矩阵
步骤1:信息规范化处理(见表2)。

表2 规范化决策矩阵
步骤2:确定正负靶心。
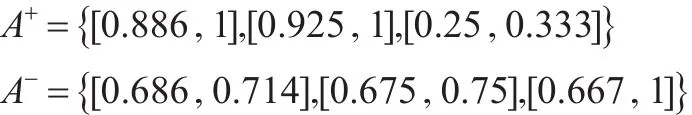
步骤3:根据2.3确定权重,计算靶心距和靶心距得分函数值。
(1)计算指标权重

求解最优化问题:

解得:W=(0.2,0.3,0.5)。
(2)计算靶心距
根据定义4,分别计算正负靶心距。

(3)计算靶心距得分函数值
根据定义6,计算靶心距得分函数值。
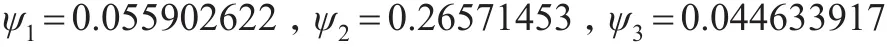
步骤4:计算投影值。

步骤5:计算灰靶决策一致性系数γi。

步骤6:基于TODIM方法计算方案全局优势度。

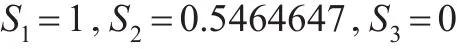
步骤7:三种方法的方案排序。

表3 不同方法结果比较
为了说明该模型的优越性,将本文排序法同靶心距得分函数方法进行比较,本文方法排序是A2>A1>A3而靶心距得分函数排序也为A2>A1>A3这两种方法排序完全一致。充分说明本文方法排序的合理性。将本文方法同TODIM法比较,TODIM法方案排序A1>A2>A3,排序结果是不尽相同,因为采用的TODIM法排序默认衰退系数θ=1,而TODIM法衰退系数取值的不同会影响方案的排序结果。而本文方法则不受其他主观因素干扰,所以排序的可信度更高,综上可以看出,与TODIM法比较而言本文方法的排序结果更值得信赖。
同时,由于决策环境信息的复杂不确定性,所以决策者只能以一般灰数的形式给出决策信息,此时很难根据现有的灰靶决策方法进行决策。而基于一般灰数的灰靶决策模型就能很好地解决这一问题,该模型是考虑方案与正、负靶心之间的距离关系,通过在改变投影方向并结合相对贴近度的思想,并利用多目标优化模型给出一种确定指标权重的方法,构建了基于一般灰数的灰靶决策模型。本文给出的案例充分说明该法对排序更加科学合理。
5 结束语
本文针对信息为一般灰数的决策问题进行了系统研究。首先,利用一般灰数来表征复杂不确定信息。其次,给出了一般灰数的距离定义。再次,利用灰靶决策的思想和相对贴近度的思想,提出了基于一般灰数的灰靶决策拓展模型,该模型有效地解决了复杂不确定信息的决策问题,其最大优点是有效解决策信息为复杂不确定性的一般灰数时,难以精确排序问题。最后,通过实际案例充分说明该模型的科学合理性,为复杂不确定信息下决策问题的研究提供了一个新的研究视角。

