随机前沿模型变量选择研究
蒋青嬗,钟世川
(广东外语外贸大学a.数学与统计学院;b.广州国际商贸中心重点研究基地,广州 510006)
0 引言
随机前沿分析(SFA)是效率测算的常用方法,在经济、管理等领域应用较广。目前SFM有大量理论和实证研究[1-3],但暂无研究涉及SFM的变量选择。变量选择对于建模非常重要。如果模型内包含较多变量,模型的复杂度增加、解释能力差且可能导致多重共线性问题。在完全共线性情况下,估计量不存在。在近似共线性情况下,估计量非有效且估计量的经济意义不合理。同时,变量的显著性检验失去意义,极可能将重要变量剔除。对于随机前沿分析,影响因素分析、要素投入比计算和技术效率测算是核心部分。变量选择有助于挑选出显著影响产出的投入,避免资源浪费。变量选择对应的参数估计的精度较高,要素投入比计算较准确,从而得出的要素分配更合理。基于上述分析,对SFM进行变量选择具有一定的可行性。
传统的变量选择方法有全部子集法和逐步回归法。该类方法效率较低且稳定性较差。当变量数目增加时可能存在维数灾难问题。考虑到传统变量选择方法的不足,惩罚方法应运而生。惩罚方法通过把较小的系数压缩为零来进行变量选择。该法较稳定且计算量较少。目前有较多变量选择的理论研究。在惩罚函数构建上,Antoniadis和Fan(2001)[4]、Fan和Li(2001)[5]提出惩罚函数的构建标准,Fan和Li(2001)[5]构造了满足上述要求的SCAD惩罚。Tibshirani和 Zou(1996)[6]分别构造了 Lasso惩罚和Alasso惩罚,Yuan和Li(2006)[7]、Wang和Leng(2008)[8]分别构造了集群Lasso惩罚和集群Alasso惩罚。
本文研究SFM的变量选择问题。随机前沿模型包含复合残差项,该项由双边误差项(刻画随机误差)和单边技术无效率项(刻画技术无效率程度)组合而成。在形式上,随机前沿模型复杂于经典的线性模型。由于复合残差项的特殊性,已有的针对于线性模型的变量选择方法并不能直接套用。本文开创性地使用Alasso惩罚方法对随机前沿模型进行变量选择,通过数值模拟考察变量选择的有效性和参数估计的效果。
1 随机前沿模型的变量选择
1.1 模型引入
引入经典的随机生产前沿模型:

其中Y=(y1,…,yN)′为因变量,衡量N个生产单元的产出;X为N×p阶自变量矩阵,衡量N个生产单元在p种要素间的投入;β=(β1,…,βp)′为参数变量;ε为复合误差项。该误差项包含两部分:v为双边随机误差,服从正态分布,即v~N(0,)。u为单边误差项,可刻画技术无效率程度,服从半正态分布,即IN表示单位矩阵。v和u相互独立且与自变量X不相关。模型中的未知参数为β,和。
对于随机前沿模型,常用的估计方法有修正最小二乘法、广义矩估计、极大似然估计和贝叶斯估计。相对来说,极大似然估计操作简单且估计量有效。接下来介绍随机模型模型的极大似然估计法,下文的变量选择方法也以极大似然估计法为基础。
对于双边误差项vi和单边技术无效率项ui,其密度函数可分别表示为:

由于vi和ui独立,i=1,…,N,故ui和vi的联合密度函数可表示为:
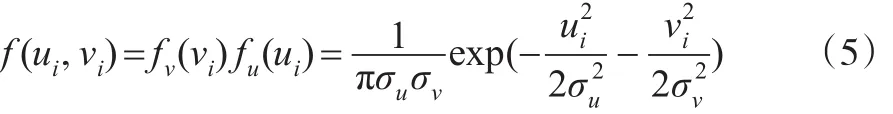
由于εi=vi-ui,从而εi和ui的联合概率密度函数为:
将f(ui,εi)对ui积分,推导可得到εi的边际密度函数:
从而模型的对数似然函数(已去除常数项)如下:

其中εi=yi-Xiβ,Xi为自变量矩阵的第i行,i=1,…,N。
式(6)的未知参数集合为φ={λ,σ2,β},最大化式(8)可得到参数估计量由于反解可得和的估计量和
1.2 变量选择方法
基于Alasso惩罚函数的优势,此处使用Alasso惩罚函数对随机前沿模型进行变量选择。随机前沿模型的待估参数集为φ={λ,σ2,β},由于只需对自变量进行选择,所以只对参数变量β施加惩罚。上述目标分两个步骤完成:
步骤1:计算基于Lasso惩罚的参数估计。

步骤2:使用参数估计获得惩罚权重,令:

该步骤的目标函数为:

步骤1和步骤2的目标函数无法得出显示解,对应的参数估计可迭代至收敛。本文取收敛规则为10-6,其中和分别为第w次和第w+1次迭代得到的估计量。不断迭代直至达到收敛规则。最终可得参数集φ的估计。
上述步骤中,参数r控制着惩罚的力度。如果r过大,较多的参数被压缩至零,容易导致欠拟合。如果r过小,无法达到变量选择的目的。常用的选取r的方法有交叉验证、AIC准则和BIC准则等,其中基于BIC准则的变量选择具有更好的稀疏性。本文的侧重点在于变量选择的准确性和模型的稀疏性,所以用BIC准则决定惩罚参数r。
步骤1和步骤2可对随机前沿模型进行变量选择并得出模型中的未知参数的估计。技术效率的测算是随机前沿模型的目标。Jondrow等(1982)[9]认为单边误差项u基于复合误差项ε的条件分布包含了复合误差中关于单边误差的所有信息,其令该条件分布的期望或者众数作为单边误差项的估计,即最终技术效率的估计为本文虽然对随机前沿模型进行变量选择,但对技术效率的估计仍可沿用JLMS方法。
推导可知ui基于εi的条件分布服从截断正态分布,即,其中。该分布的期望或者众数可作为技术无效率项的点估计,即:

相应技术效率的估计为TEi=exp(-ui),其中ui为ui的点估计。
2 蒙特卡罗模拟
本文模拟的目的在于考察变量选择的准确性及参数估计的精度。对于变量选择的准确性,考察了三个衡量指标:①重要变量被错误剔除的比例。②非重要变量被正确剔除的比例。③正确识别真实模型的比例。如果第一个指标越小,那么第二个和第三个指标就越大,变量选择的准确性也越高。对于参数估计的精度,考察估计量的偏差、标准差和均方误差。如果上述三个指标越小,则参数估计的精度越高。
此处设计如下三组模拟:
(1)取N=300,p=6,考虑如下随机前沿模型:

其中X为N×p阶自变量矩阵,X内的元素服从(1,5)的均匀分布。由于本文着重于变量选择,为了模拟的简洁性,此处的模拟不包含截距项;(β1,β2,β3,β4)=(1,2,3,4) ;随机误差项v~N(0,IN) ,无效率项u~N+(0,22IN),从而的真值为2的真值为5。
(2)取N=500,其余的定义同模拟(1)。
(3)取N=800,其余的定义同模拟(1)。
模拟(2)和模拟(3)的样本容量大于模拟(1),有助于分析大样本下的效果。在模拟分析时,本文同时采用普通极大似然估计方法对随机前沿模型进行估计并比较本文提出方法(用AVS表示)和普通极大似然估计方法(用LME表示)在变量选择和参数估计方面的表现。基于上述方法的模拟(1)、模拟(2)和模拟(3)均模拟200次。分析结果如表1和表2所示:

表1 变量选择的准确性 (单位:%)

表2 参数估计的效果
由表1可知,AVS法和LME对应的指标NZZ均为0,这表明虽然本文侧重于变量选择,但AVS法和LME均不会把重要变量剔除掉,重要变量的可靠性得到保证。同时,由于进行变量选择后随机前沿模型仍包含所有的重要变量,所以不会造成遗漏变量、参数估计有偏和不一致的问题。AVS法对应的指标ZZ和Z远高于LME,这说明AVS法能以较高的正确率将模型中的非重要变量剔除掉并识别出真实模型,变量选择的准确度较高。当样本容量增加时,AVS法对应的指标ZZ和Z小幅度增加,变量选择的准确性也增加。而LME因其较低的准确率基本不具备变量选择的功能。虽然随着样本容量的增加,LME对应的指标ZZ和Z增加,但仍处于较低的水平,故可认为LME基本不具备变量选择的功能。
表2清楚地展示了AVS法和LME法对应参数估计的偏差、标准差和均方误差。β5、β6的真值为零且AVS和LME能以较高的比例剔除掉这两个参数对应的变量,故此处不考虑β5、β6的参数估计效果。由于变量个数、指标数较多,为更直观简洁地比较AVS法和LME的参数表现,此处把AVS法和LME得出的参数估计的偏差、标准差和均方误差分别提取出来并绘制成如图1。参数β1、β2、β3、β4和参数λ、σ2在偏差、标准差和均方误差方面相差较大,故此处把β1、β2、β3、β4和λ、σ2分开处理。图 1(a)、图1(c)、图 1(e)分别对应β1、β2、β3、β4的估计在模拟(1)、模拟(2)、模拟(3)处的偏差、标准差和均方误差,图1(b)、图1(d)、图1(f)分别对应λ、σ2的估计在模拟(1)、模拟(2)、模拟(3)处的偏差、标准差和均方误差。每个图包含两条线,AVS和LME。判断AVS法是否优于LME法即为判断AVS线是否有较多的点位于LME线的下方。
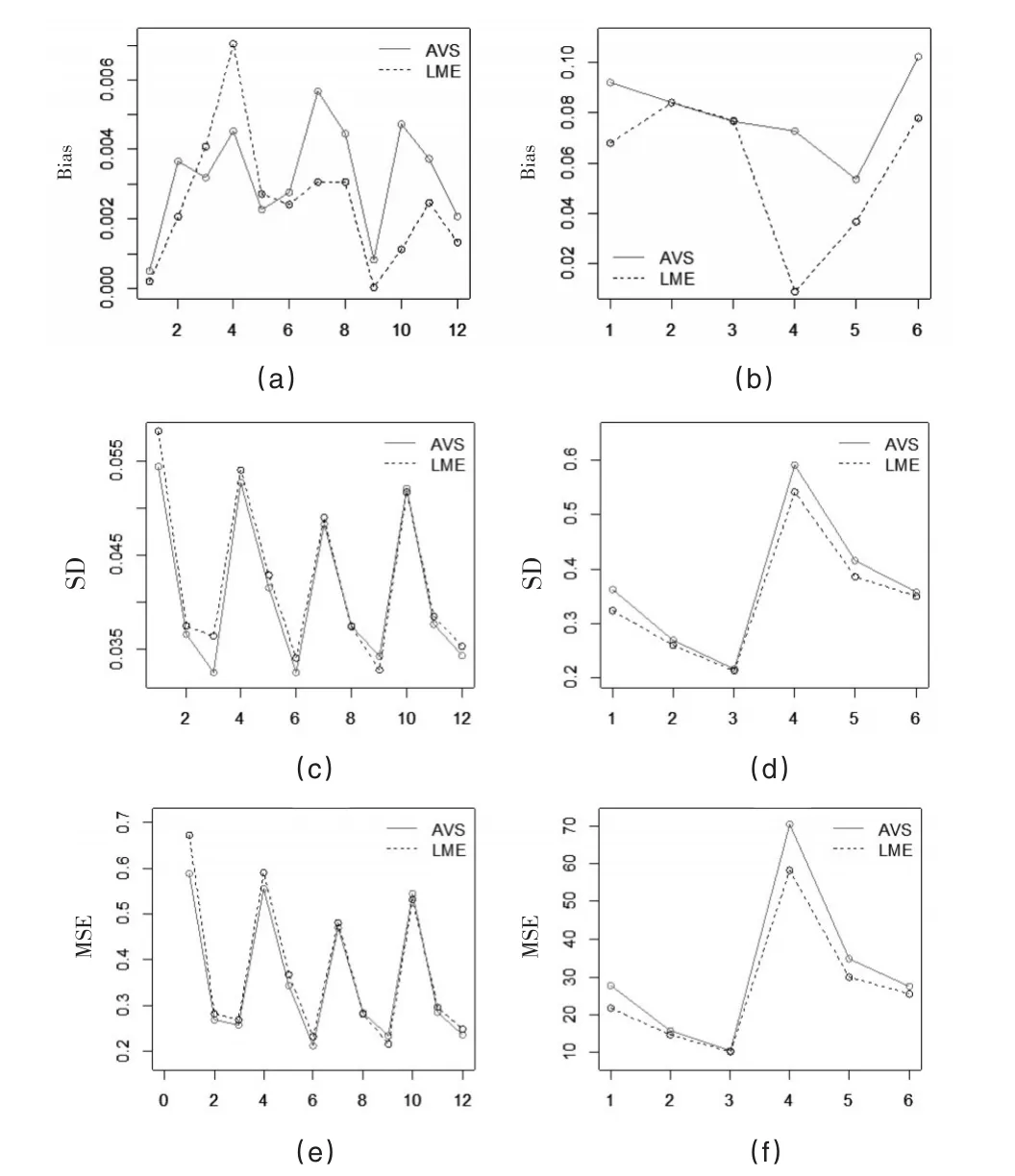
图1 AVS法和LME估计效果比对
从图1(a)中可知,AVS线大部分位于LME线的上方。12个点中,AVS有9个点高于LME。对于AVS线,第1、2、3点先上升后下降,第4、5、6点先下降后上升,第7、8、9点和第10、11、12点均连续下降。对于LME线,第1、2、3点连续上升,第4、5、6点连续下降,第7、8、9点平行下降,第10、11、12点先上升后下降。从图1(b)中可知,AVS线几乎完全位于LME线的上方。6个点中,AVS有5个点高于LME。对于AVS线,第1、2、3点连续下降,第4、5、6点先下降后上升。对于LME线,第1、2、3点先上升后下降,第4、5、6点连续上升。上述分析表明AVS法的参数估计的偏差大于LME。随着样本量的增加,部分参数估计的偏差绝对值增加,部分参数估计的偏差绝对值减少,偏差的表现不稳定。
从图1(c)中可知,AVS线大部分位于LME线的下方。12个点中,AVS有10个点低于LME。对于AVS线,第1、2、3点,第4、5、6点,第7、8、9点和第10、11、12点均连续下降。LME线也如此。从图1(d)中可知,AVS线完全位于LME线的上方,AVS的6个点均高于LME。对于AVS线,第1、2、3点和第4、5、6点均连续下降。LME线也如此。上述分析表明,对于参数β1、β2、β3、β4,AVS法的标准差低于LME,这说明变量选择方法能有效减少自变量对应的参数估计的标准差。对于参数λ和σ2,AVS法的标准差要高于LME。随着样本容量的增加,AVS法和LME对应的标准差均逐渐减少。
从图1(e)中可知,AVS线大部分位于LME线的下方。12个点中,AVS有10个点低于LME。对于AVS线,第1、2、3点,第4、5、6点,第7、8、9点和第10、11、12点均连续下降。LME线也如此。从图1(f)中可知,AVS线完全位于LME线的上方,AVS的6个点均高于LME。对于AVS线,第1、2、3点和第4、5、6点均连续下降。LME线也如此。上述分析表明,对于参数β1、β2、β3、β4,AVS法的均方误差低于LME。对于参数λ和σ2,AVS法的均方误差均高于LME。该结果较好理解。参数λ和σ2的估计与残差密切相关,引入越多的变量,残差会拟合得越好。
综上可知,对于自变量对应参数β1、β2、β3、β4,AVS法的估计效果优于LME法。对于参数λ和σ2,AVS法的估计效果次于LME法。
3 结论
本文首次使用Alasso惩罚方法对随机前沿模型进行变量选择和参数估计,Alasso惩罚方法为连续最优化过程,具有较好的稳定性和较少的计算量。接着使用蒙特卡罗模拟考察变量选择的准确性和参数估计的效果。
模拟结果表明:(1)随机前沿模型常用的LME方法基本不具备变量选择的功能,LME方法不能有效识别模型中非重要的要素投入。(2)AVS能以较高的准确率剔除非重要变量、保留重要变量和识别真实模型,变量选择的准确性较高。所以在进行影响因素分析时,AVS法的结果更为可靠。(3)对于自变量对应的参数估计,AVS法的偏差大部分高于LME,但标准差和均方误差均低于LME,这说明变量选择方法能有效减少自变量对应的参数估计的标准差和均方误差,从而使自变量对应的参数估计的精度增加,参数估计的总体效果更优。在进行要素投入比计算或者影响因素分析时,使用AVS法较优。
基于上述模拟分析可知,文中方法在要素投入比计算和影响因素分析时较有效,因此可将模型应用到此类问题的分析中。变量选择对应的参数估计的精度较高,要素投入比计算较准确,从而得出的要素分配更合理。此外,变量选择也有助于挑选出显著影响产出的投入,从而生产单元无需过多关注不显著的投入,避免了资源浪费。本文模型以产出随机前沿模型为基础,做少许变化即可把文中方法应用到成本随机前沿模型。面板数据同时考虑了空间相关性性和时间依赖性,具有更高的自由度和更丰富的信息量。文中方法也可顺利拓展到面板随机前沿模型的变量选择。

