端部状态对斜置圆柱气动力分布的影响
马文勇, 汪冠亚, 郑 熙, 陈 铁, 李 智, 张程远, 方平治
(1. 石家庄铁道大学 土木工程学院, 石家庄 050043; 2. 长江三峡集团 福建能源投资有限公司, 福州 350003; 3. 中国气象局 上海台风研究所, 上海 200030)
0 引 言
圆柱是土木工程、航空航天工程、机械工程、海洋工程等领域常见的细长结构形式之一[1],如输电导线、斜拉桥拉索、桥塔、烟囱等,其风荷载取值都是以圆柱结构气动力为原型建立起来的。这些结构长细比大、柔度高、易发生风致大幅振动,常见的振动形式有烟囱的涡激振动、输电导线的驰振、斜拉索的风雨振等。
在细长柱体结构的风荷载测试中,当模型端部直接连接于风洞壁面时,壁面边界层会在连接处产生马蹄涡,从而影响流动状态;当模型端部与风洞壁面有一定距离时,自由端的三维流动又会对柱体尾流产生影响;而加装端板就是为了减小壁面边界层和自由端分离对流动状态的影响。Stansby[2]通过风洞试验研究了端板对圆柱基准风压系数的影响,表明端板可以降低基准压力、增加阻力;Fox等[3]指出端板是确保直圆柱绕流“二维”流动的条件,为确保中间“二维”流动的区域,两端板间距必须大于7倍圆柱直径;Inagaki等[4]研究了端部状态和长细比对圆柱表面气动力的影响,指出当长细比较大时,端部边界层越薄,中间的阻力系数越大;郑云飞等[5]指出当长细比较小时,端部状态不仅对端部附近的风压有影响,对中间部分也有很大影响。
上述研究大多是针对端部状态对直圆柱气动力的影响,而对斜置圆柱的研究则相对较少。Shirakasi等[6]首次在斜置圆柱背风面发现了沿轴向的“次流动”,并证实了该流动是扰乱规律性旋涡脱落的主要原因;Matsumoto等[7]证实了“次流动”的存在,将其命名为“轴向流”,指出轴向流的存在会减小升力;Hayashi等[8]研究了两端有端板的有限斜置圆柱表面风压分布,将圆柱轴向风压分布分为3个区域:近上游端板区、中间区和近下游端板区;顾明等[9]对无端板情况下风向角对倾斜拉索表面风压分布和大小的影响进行了研究;李寿英等[10]对斜置圆柱的绕流进行了CFD模拟,指出斜置圆柱绕流与直圆柱绕流有很大差异;马文勇等[11]通过风洞试验对临界雷诺数下斜置椭圆柱的绕流进行了研究,指出斜置椭圆柱和直椭圆柱有很大不同,斜置椭圆柱可以增加截面有效面积,从而促使流体在其表面重新附着。目前,针对倾角较大时端部状态变化对斜置圆柱气动力影响的研究仍然比较缺乏。
本文通过刚性模型风洞测压试验测试3种端部状态下的平均风压系数沿轴向和周向的分布变化以及阻力系数变化,分析端部状态对斜置圆柱气动力分布的影响,为斜置细长柱体的静态、动态风洞试验研究提供建议。
1 试验概况
1.1 试验设备及模型
试验在石家庄铁道大学STDU-1风洞实验室低速试验段内进行。试验段宽4.4m、高3m、长24m,风速0~30m/s连续可调。在23m/s风速下,试验段中心区域速度场不均匀性小于0.5%,背景湍流度小于0.5%。采样时长30s,采用电子压力扫描阀测试压力(量程±2540Pa,精度±0.15%,采样频率330Hz),并对压力信号进行修正[12]。
试验模型采用有机玻璃制作,直径d=180mm,模型中心安装直径40mm的钢管以提高模型刚度,并通过钢管将模型两端固定于钢架上。模型长度随着圆柱倾角β(模型轴向与垂直于来流平面的夹角[13])的不同而变化。沿模型轴向布置4圈测点A、B、C、D,与模型轴向中心的距离分别为1300、650、0和780mm;每圈周向布置44个测压孔,测压孔位置以周向角θ表示;沿模型轴向布置4排测点,其对应的周向角θ为0°、90°、180°和270°,每两个测点的间距为100mm。为方便描述圆柱轴向测点到两端导流板的距离,建立如图1(a)所示的x-y坐标系,坐标系原点为斜置圆柱中央断面与圆柱中心轴的交点。
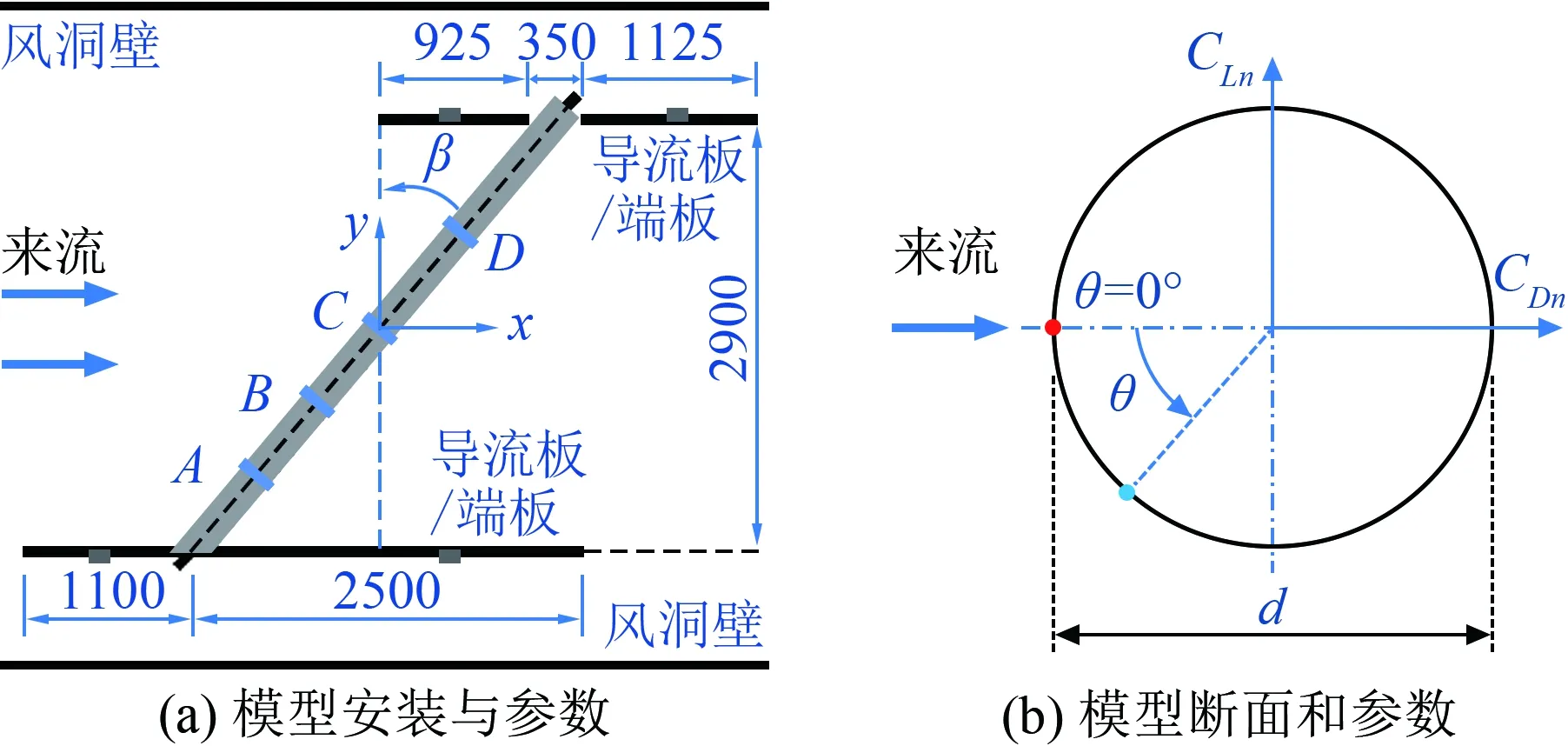
图1 模型及试验参数定义
为减小模型两端的钢架对端部流动的影响,在钢架上固定导流板。上游导流板长3.6m、宽1.2m,下游导流板长2.4m、宽1.2m。在两个导流板上开直径0.35m的圆孔,便于将钢管固定在钢架上。
1.2 试验工况
试验风速为5.4m/s,对应的雷诺数Re≈6.43×104,圆柱倾角β=60°,此时模型长度为6m。对于斜置圆柱气动力试验,消除端部效应和保证轴向流动是试验面临的两个主要问题。试验中,圆柱体两端平行流向安装有导流板,当导流板封闭时,与端板作用类似,此时也可称为端板。因此,共采用4种工况:
工况1(图2(a)):上下游导流板都不封闭。导流板减弱了钢架对端部流动的影响,但是柱体两端无端板,轴向流动不受限制,同时上游自由端的绕流也并未消除;
工况2(图2(b)):上下游导流板都封闭,相当于两端均安装了端板的斜置圆柱;
工况3(图2(c)):上游导流板封闭、下游不封闭。此时消除了上游自由端的绕流影响,同时使轴向流在下游端不受阻碍;
工况4(图2(d)):在工况3的基础上,在圆柱上距离C圈测点160mm的下游位置,增加一个与导流板平行的直径350mm的圆形挡板,挡板与圆柱同心,以说明端板本身对已经形成的轴向流的影响。
为方便与已有研究成果对比,也对β=0°的直圆柱进行了研究,此时模型长度为2.9m。


图2 4种试验工况照片
1.3 试验参数
风压系数Cpnθ(t)、平均升力系数CLn、平均阻力系数CDn和雷诺数Ren定义如下:
(1) 风压系数Cpnθ(t):
(1)
式中:P(θ)为测点处风压,P0为静压;ρ为空气密度;U为来流风速。平均风压系数以Cpn表示,驻点(θ=0°)、下测点(θ=90°)、背风点(θ=180°)、上测点(θ=270°)对应的平均风压系数分别为Cpnst、Cpnd、Cpnb和Cpnu。
(2) 平均升力系数CLn、平均阻力系数CDn:

式中:Cpn(θ)为测点平均风压系数;N为周向测点个数44。本文的阻力系数和升力系数是基于风速的垂直分量的风压系数积分得到的,这种方法有利于检验是否可以将斜置圆柱等效为风速的垂直分量作用下的垂直圆柱,方便与垂直圆柱的结果进行对比。采用此方法得到的阻力系数与传统意义的阻力系数有一定差异,即阻力方向垂直于结构轴向但并不平行于来流方向。
(3) 基于风速的垂直分量计算的雷诺数Ren:
(3)
式中,ν为运动粘性系数,一般取1.5×10-5。
1.4 试验结果的验证
当Re=6.43×104、β=0°、两端导流板封闭时,平均风压系数沿断面周向的分布与相似试验条件的文献[14]的结果基本一致,如图3所示。在此雷诺数下,平均风压系数沿断面周向对称分布,这也与典型的圆形断面亚临界风压系数分布特点相吻合。A~D圈测点的数据重合性较好,说明模型及流场沿轴向比较均匀。

图3 β=0°时的风压系数分布
2 试验结果
2.1 端部状态对直圆柱气动力的影响
文献[13]指出,在直圆柱(β=0°)绕流中,导流板与端板的作用类似,都是减小端部影响,防止端部形成三维流动,使流动更加接近二维流动。本文通过两种端部状态对直圆柱气动力开展研究:
(1) 两端导流板都不封闭。对应的4圈测点位置命名为A1、B1、C1、D1,相应的气动力系数以下标1区分:Cpn1、Cpnst1、Cpnd1、Cpnb1、Cpnu1、CDn1;
(2) 两端导流板都封闭。对应的位置和气动力系数以下标2区分:A2、B2、C2、D2、Cpn2、Cpnst2、Cpnd2、Cpnb2、Cpnu2、CDn2。
图4为4排测点的风压系数沿轴向的分布,可以看出:
(1) 在两种端部状态下,驻点风压系数沿轴向的分布几乎无变化(都在1.0左右),说明端部状态的变化对驻点附近的风压分布几乎无影响。
(2) 两端导流板封闭时,背风点风压系数在-1.4左右,上下测点风压系数在-1.2左右,且都沿轴向变化不大,说明此时风压沿轴向分布均匀。
(3) 两端导流板不封闭时,背风点和上下测点的风压系数沿轴向可分为近端部区和中间区:
在近端部区(y/d<-4和y/d>4),背风点风压系数沿轴向呈现先增大后减小的趋势,最小风压系数在关于模型轴向中心对称的y/d=-7和7的位置;离端部越近,上下测点的风压系数绝对值越大。
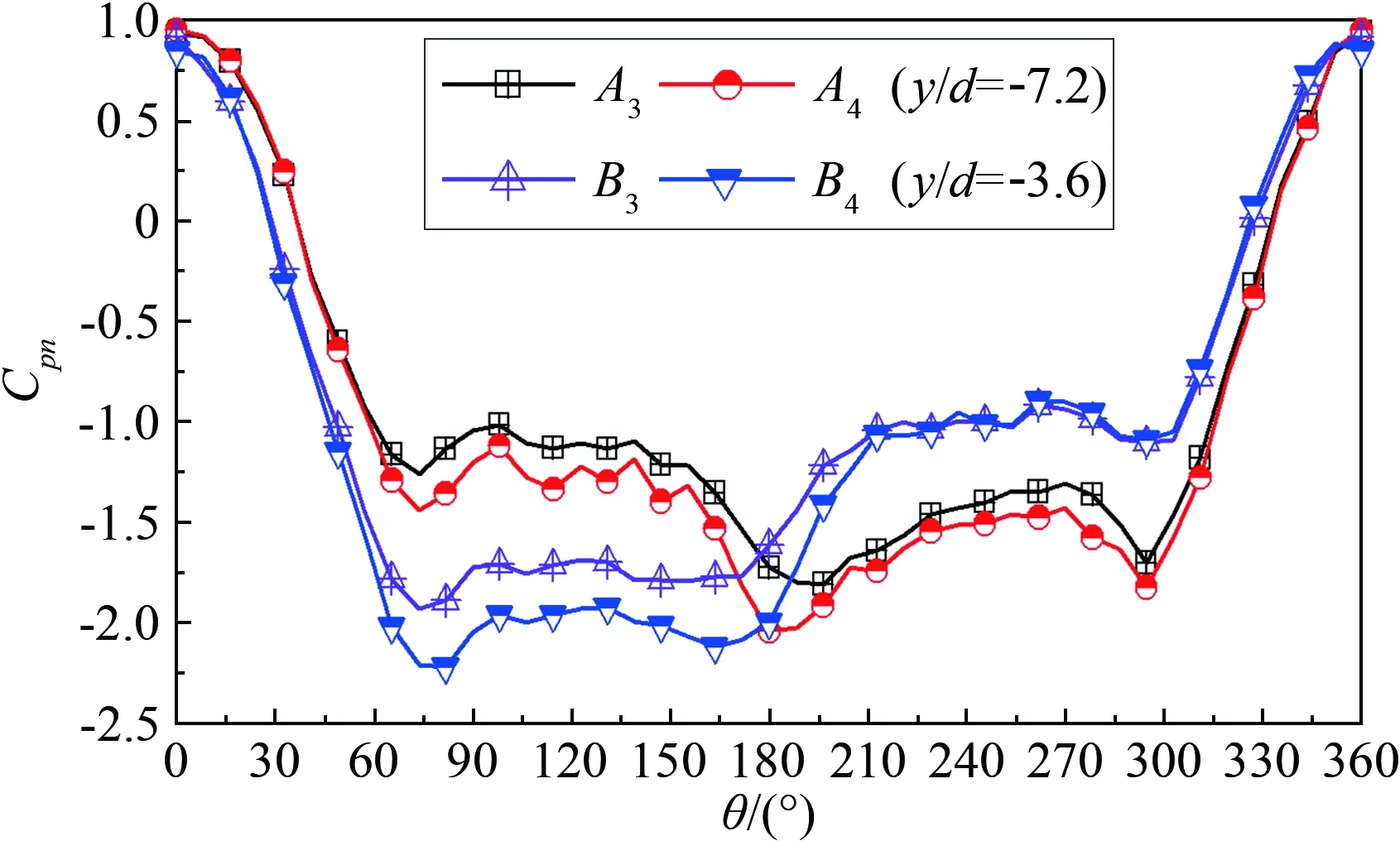
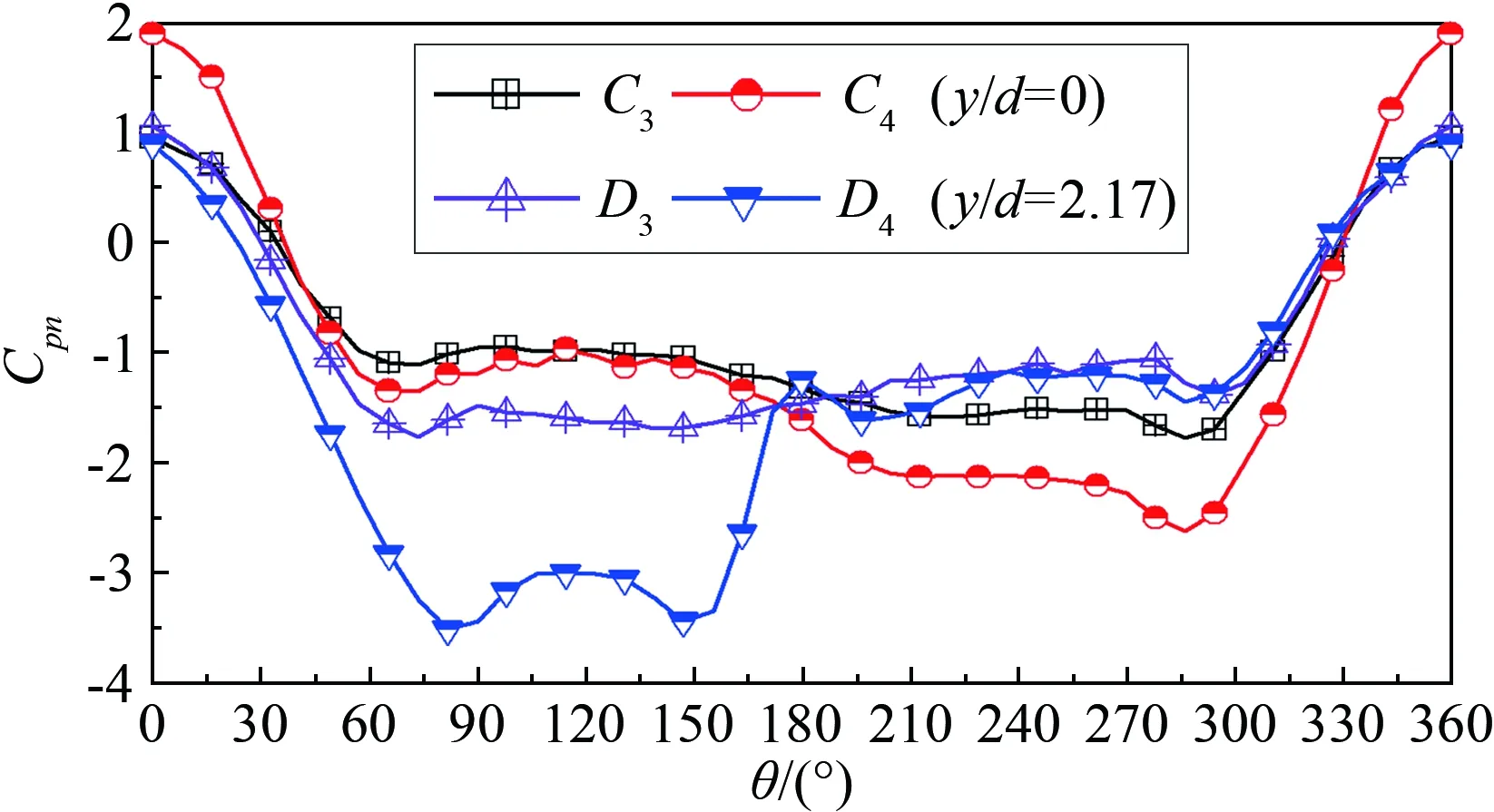
在中间区(-4 (a) 驻点和背风点(θ=0°和θ=180°)沿轴向的风压系数分布 (b) 上下测点(θ=270°和θ=90°)沿轴向的风压系数分布 总之,两端导流板封闭时,风压沿轴向分布均匀;两端导流板不封闭时,风压分布的均匀性发生改变:风压分布均匀区由整个圆柱(-8 图5为A~D圈的风压系数沿周向的分布(A圈位于近端部区,其他圈位于中间区)。由图5可知: (1) 两端导流板不封闭时,B、C、D圈的风压系数分布几乎相同,A圈则与B、C、D圈有很大差别,可能是近端部区的流动受导流板影响造成的。此时,A~D圈对应的阻力系数为1.35、0.93、0.91、0.93,这与ESDU[16]建议的取值范围相差较大。 (2) 两端导流板封闭时,A~D圈的风压系数分布几乎重合,再次说明了两端导流板封闭时各个周向的风压沿轴向分布的均匀性。此时对应的阻力系数为1.31、1.32、1.29、1.27,与ESDU建议的取值范围接近(本文的试验值未进行阻塞度修正)。 (3) 在θ=0°~40°和320°~360°范围内,无论两端导流板封闭或不封闭,中间区的周向风压系数分布几乎无变化;而在θ=40°~320°范围内,两端导流板不封闭时的风压系数大于封闭时的风压系数。 (4) 从A圈可以看出,在两种端部状态下,在θ=0°~60°和270°~360°范围内,近端部区的周向风压系数分布重合;而在θ=60°~270°范围内,风压系数分布有很大差别,说明端部状态的改变对尾流区的风压系数有很大影响。 (a) A圈和B圈的风压系数分布 (b) C圈和D圈的风压系数分布 在直圆柱绕流中,端板(封闭导流板)可以有效减小自由端影响;而在斜置圆柱绕流中,端板的作用有很大的不同。通过3种工况对斜置圆柱开展研究: (1) 两端导流板不封闭。对应的位置和气动力系数为:A1、B1、C1、D1、Cpn1、Cpnst1、Cpnd1、Cpnb1、Cpnu1、CDn1; (2) 两端导流板封闭。对应的位置和气动力系数为:A2、B2、C2、D2、Cpn2、Cpnst2、Cpnd2、Cpnb2、Cpnu2、CDn2; (3) 上游导流板封闭,下游导流板不封闭。对应的位置和气动力系数为:A3、B3、C3、D3、Cpn3、Cpnst3、Cpnd3、Cpnb3、Cpnu3、CDn3。 图6为β=60°、Ren=3.25×104时,3种工况下驻点平均风压系数Cpnst和背风点平均风压系数Cpnb的分布。参照文献[8]的研究方法,把圆柱沿轴向的风压分布分为3个区域:近上游端部区、中间区和近下游端部区。由图6可知: (1) 在近上游端部区y/d=-8处,驻点处的风压系数Cpnst2≈Cpnst3>Cpnst1,说明气流流过圆柱上游端部时,导流板的封闭阻止了部分气流绕过端部的流动。在-8 (2) 在中间区-6 (3) 在近下游端部区6 图6 驻点和背风点的风压系数分布 图7为β=60°时、上下测点对应的平均风压系数沿轴向的分布。在近上游端部区,当-8 图7 上下测点的风压系数分布 Fig.7Windpressurecoefficientdistributionatbothflanks,CpndandCpnu 综上所述,斜置圆柱沿轴向的风压分布可分为3个区域:近上游端部区、中间区、近下游端部区。在近上游端部区的背风面会形成马蹄涡,受轴向流作用会向中间区流动,使中间区的风压分布产生交替变化;导流板的封闭会增加马蹄涡的强度和风压交替变化的幅度。 图8为A~D圈的周向风压系数分布。在圆柱迎风面(即330°<θ<360°和0°<θ<30°的区域),在不同端部状态下,A~D圈的风压系数分布基本相同,说明端部状态变化对迎风面风压系数分布几乎无影响;随着θ的增大,在不同端部状态下,A~D圈的风压系数分布呈现不同的变化形式,说明端部状态对背风面风压分布有较大影响。 (a) A圈的风压系数分布 (b) B圈的风压系数分布 (c) C圈的风压系数分布 (d) D圈的风压系数分布 从图8(a)可以看到,两端导流板都封闭时,A圈背风点的风压系数最小,两端都不封闭时最大,即Cpnb1>Cpnb3>Cpnb2。对应A圈的阻力系数CDnA1、CDnA2、CDnA3分别为1.34、1.55、1.38,这说明两端导流板的封闭可以减小A圈背风点风压系数,增大其阻力系数。 与对A圈的影响类似,B圈的阻力系数CDnC1(1.22) 从图8(c)可以看到,导流板封闭状态对C圈风压系数的影响与对B圈的影响类似(见图8(b)),CDnC1(1.20) 从图8(d)可以看到,D圈的风压系数分布形式与B圈相似,端部状态的改变同样也主要影响圆柱背风面下表面(θ=80°~180°)的风压系数分布。 A~D圈的风压系数分布变化对应了前文上下测点风压系数沿轴向的交替变化。 综上所述,端部状态的改变主要影响背风面的风压分布,而对迎风面驻点附近的风压分布无太大影响;在沿轴向的中间区,周向分布的最强负压会交替出现在背风面上表面和下表面,这一现象反映出流体绕斜置圆柱流动具有很强的三维特性;端部状态对中间区的阻力系数有较明显影响,两端导流板的封闭可以使中间区的阻力系数增加。 在以上研究中,A~D圈的测点主要分布于中间区。为了研究近上游端部区的周向风压分布以及近下游端部区的周向和轴向风压分布,选取上游导流板封闭、下游导流板不封闭的工况,在y/d=0.89位置增加一个直径为350mm的挡板,顺风向放置,A、B、C圈测点在挡板上游,D圈在挡板下游,对应的位置和气动力系数为:A4、B4、C4、D4、Cpn4、Cpnst4、Cpnd4、Cpnb4、Cpnu4、CDn4、CLn4。 图9为有挡板时驻点和背风点沿轴向的风压系数分布。主要针对近挡板区域的风压分布进行研究,可以看出:(1) 在挡板的上游附近,驻点风压系数分布曲线有一个凸起的尖角,其他位置驻点的风压系数基本不变,说明此时气流在挡板上游附近聚集,使此处产生较大压力,这一结果与前文两端导流板封闭时的情况一致;(2) 在挡板位置上游,背风点风压系数分布曲线也有一个凸起的尖角,此尖角比迎风面的尖角小,说明挡板对上游迎风面风压影响较大;(3) 挡板上下游的风压系数差异较大,其变化形态与上游导流板封闭时上游导流板附近的风压分布形态相似,说明此时挡板下游的流动状态和上游导流板封闭时的流动状态相似。 图9 驻点和背风点的风压系数分布 Fig.9WindpressurecoefficientdistributionforCpnstandCpnb 图10为有/无挡板时上下测点(θ=270°和90°)沿轴向的风压系数分布。可以看出:(1) 在靠近上游导流板的区域,风压系数分布曲线几乎重合,说明有/无挡板对此区域的风压分布几乎无影响;(2) 有挡板时,在-4 图10 上下测点的风压系数分布 Fig.10Windpressurecoefficientdistributionatbothsides,CpndandCpnu 图11为有/无挡板时A~D圈的风压系数分布。由图11(a)可知:(1) 在A圈0°<θ<60°、300°<θ<360°和B圈0°<θ<55°、210°<θ<360°范围内,有/无挡板时的风压系数分布无太大差别;(2)有挡板时,在A圈60°<θ<300°和B圈55°<θ<210°范围内的风压系数绝对值增大,且B圈的增大幅度比A圈的更大,说明离挡板越近,挡板对风压分布的影响越大。 从图11(b)可以看出:(1)在C圈迎风面0°<θ<30°和330°<θ<360°范围内,有挡板比无挡板时的风压系数要大,这是因为C圈距离挡板较近,在迎风面出现了气流聚集;(2)在D圈0°<θ<180°范围内,风压系数分布有很大差别,结合图9可知,在挡板下游的D圈背风面下表面,出现了一个绝对值很大的负压。由此可知:在上游近挡板区,挡板主要影响迎风面风压分布;在下游近挡板区,主要影响背风面风压分布。 (a) A、B圈风压系数分布 (b) C、D圈的风压系数分布 综上所述,有挡板时,挡板的上下游可分为上游近挡板区和下游近挡板区;挡板对近上游端部区的风压分布影响不大,主要影响上下游近挡板区和近下游端部区;加挡板后,驻点和背风点沿轴向的风压系数分布曲线在上游近端部区出现了突变(尖角),且驻点突变的幅度大于背风点,说明挡板对迎风面的影响大于背风面;上游近挡板区的风压分布趋势与近上游端部区相似。 通过刚性模型测压试验,对Re=6.43×104时不同端部状态下的直圆柱(β=0°)和斜置圆柱(β=60°)气动力进行了研究(主要研究了端部状态改变对风压系数分布和阻力系数的影响),得到以下结论: (1) 对于直圆柱而言,即使本文模型的长细比已经达到16,自由端仍然对风压分布有较大影响。在不使用端板的情况下,虽然圆柱中间区的风压沿轴向均匀分布,但其阻力系数仍远小于二维圆柱的对应值,基准风压也明显小于二维圆柱的对应值。因此,对于模拟准二维圆柱的气动力测试试验,端板非常必要。 (2) 轴向流是斜置圆柱的一个重要流动特征,端板和轴向流之间存在复杂的相互影响关系:端板可能阻碍轴向流发展,轴向流也可能将端板本身的影响进一步传递。在下游位置的封闭导流板(端板)或者挡板,都会阻碍来自上游的轴向流;在上游位置的封闭导流板(端板)或者挡板,会形成马蹄涡并沿轴向传向下游,形成交替的上下表面风压变化;从影响范围上来看,端板或挡板对上游轴向流的影响范围要小于对下游的影响范围。 (3) 对于大角度斜置圆柱,端板本身所产生的影响范围会随着轴向流的发展而扩大,采用端板消除端部效应的手段会适得其反。因此,相比于垂直圆柱,斜置圆柱需要更大的长细比才能模拟准二维流动。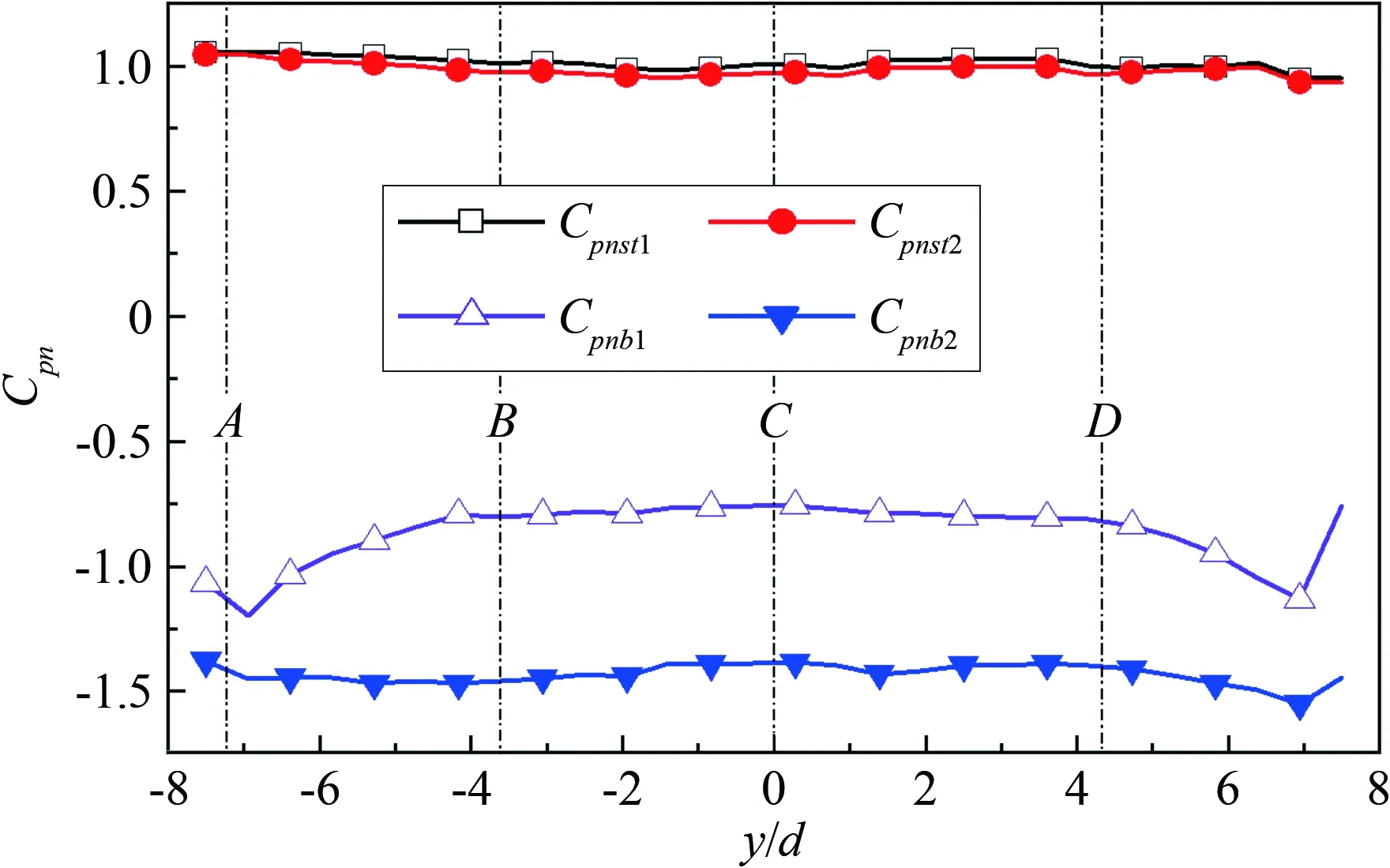
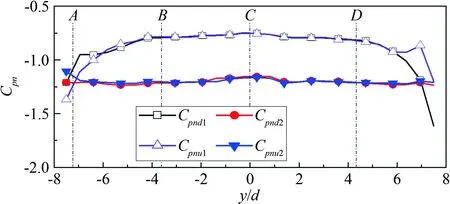


2.2 端部状态对斜置圆柱轴向风压分布的影响

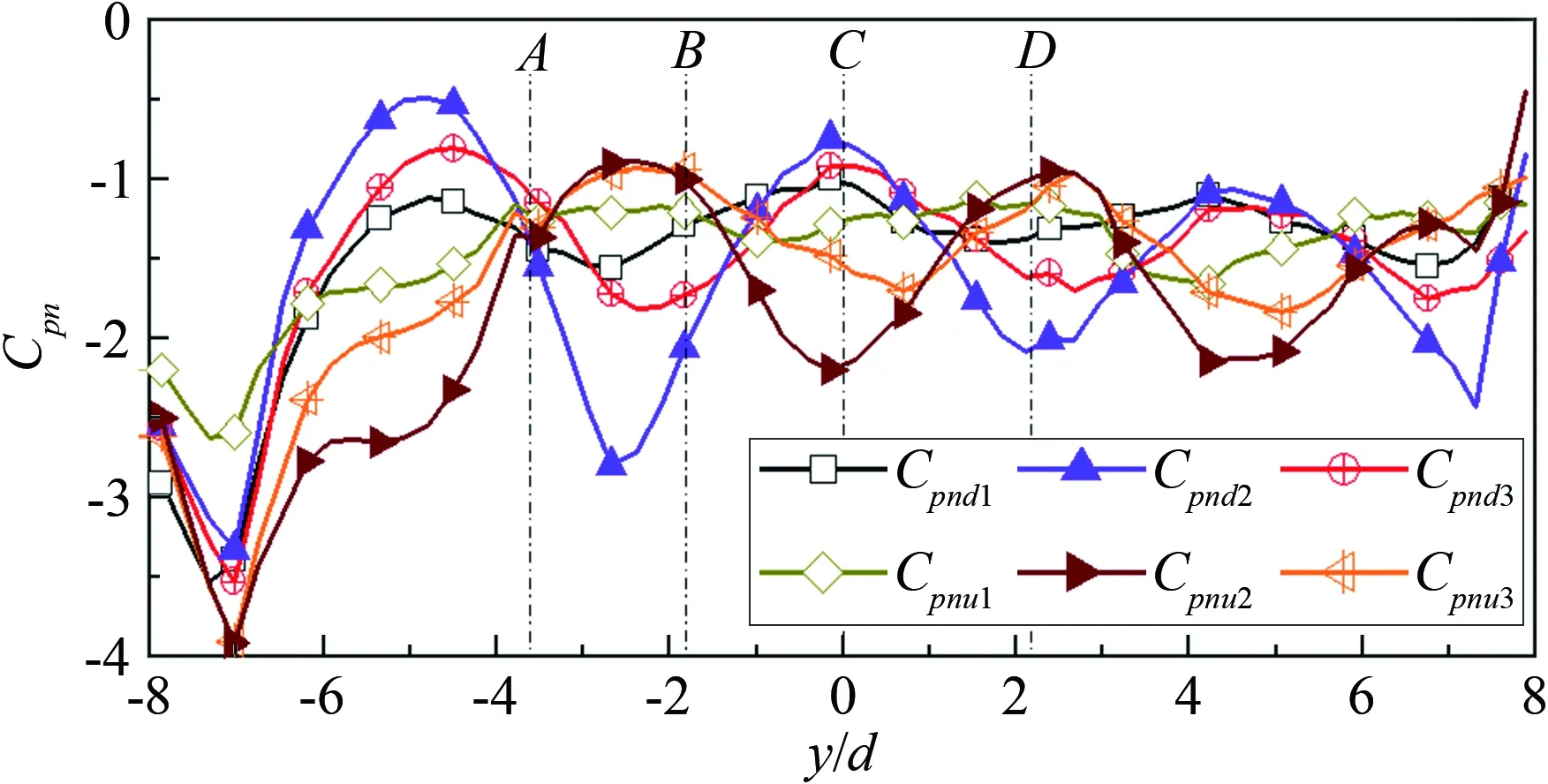
2.3 端部状态对斜置圆柱周向风压分布的影响

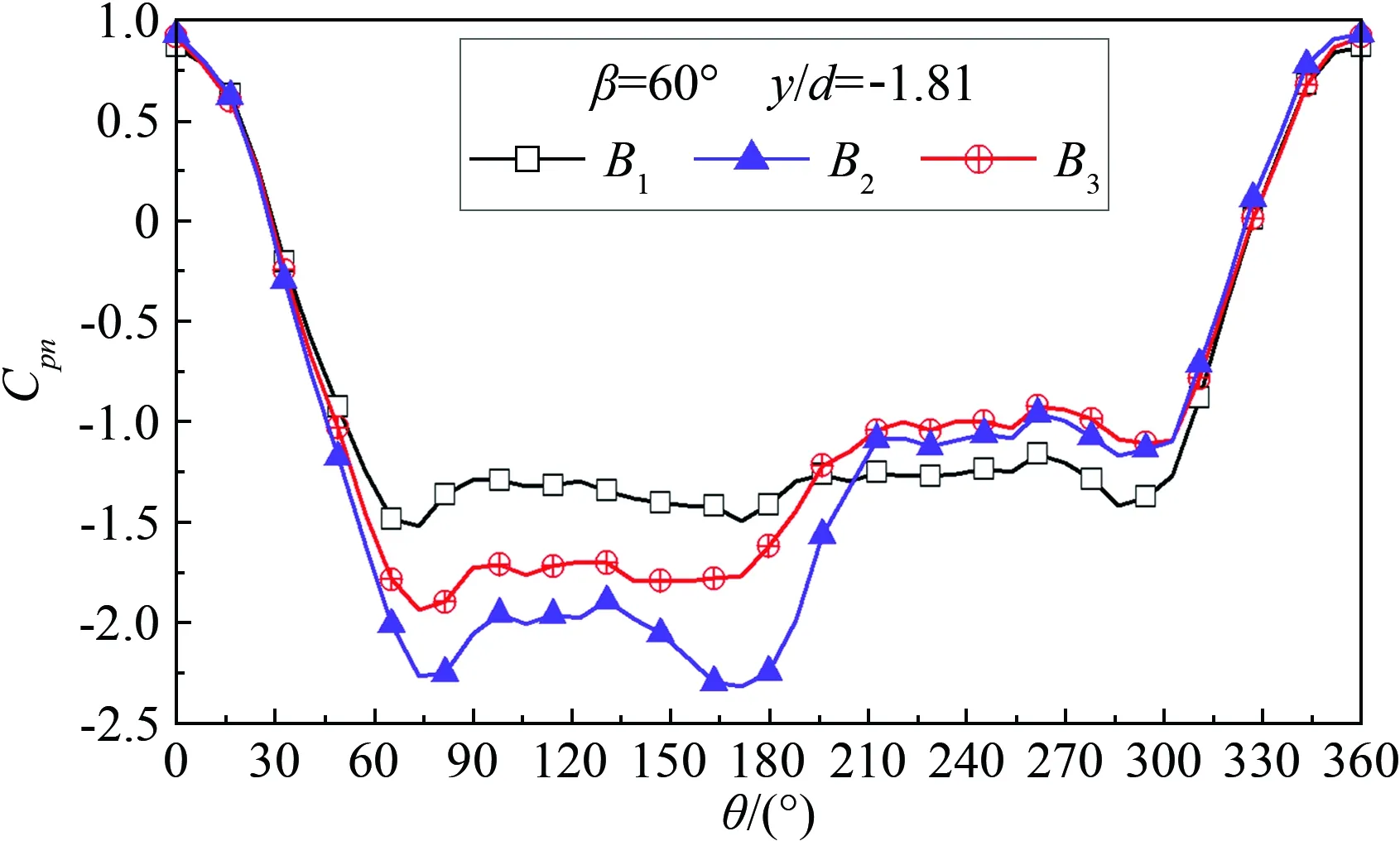
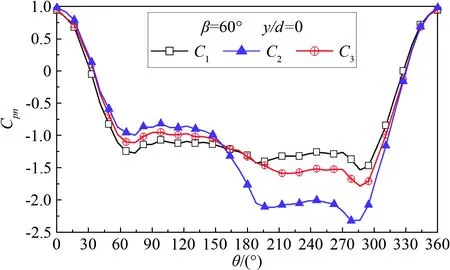
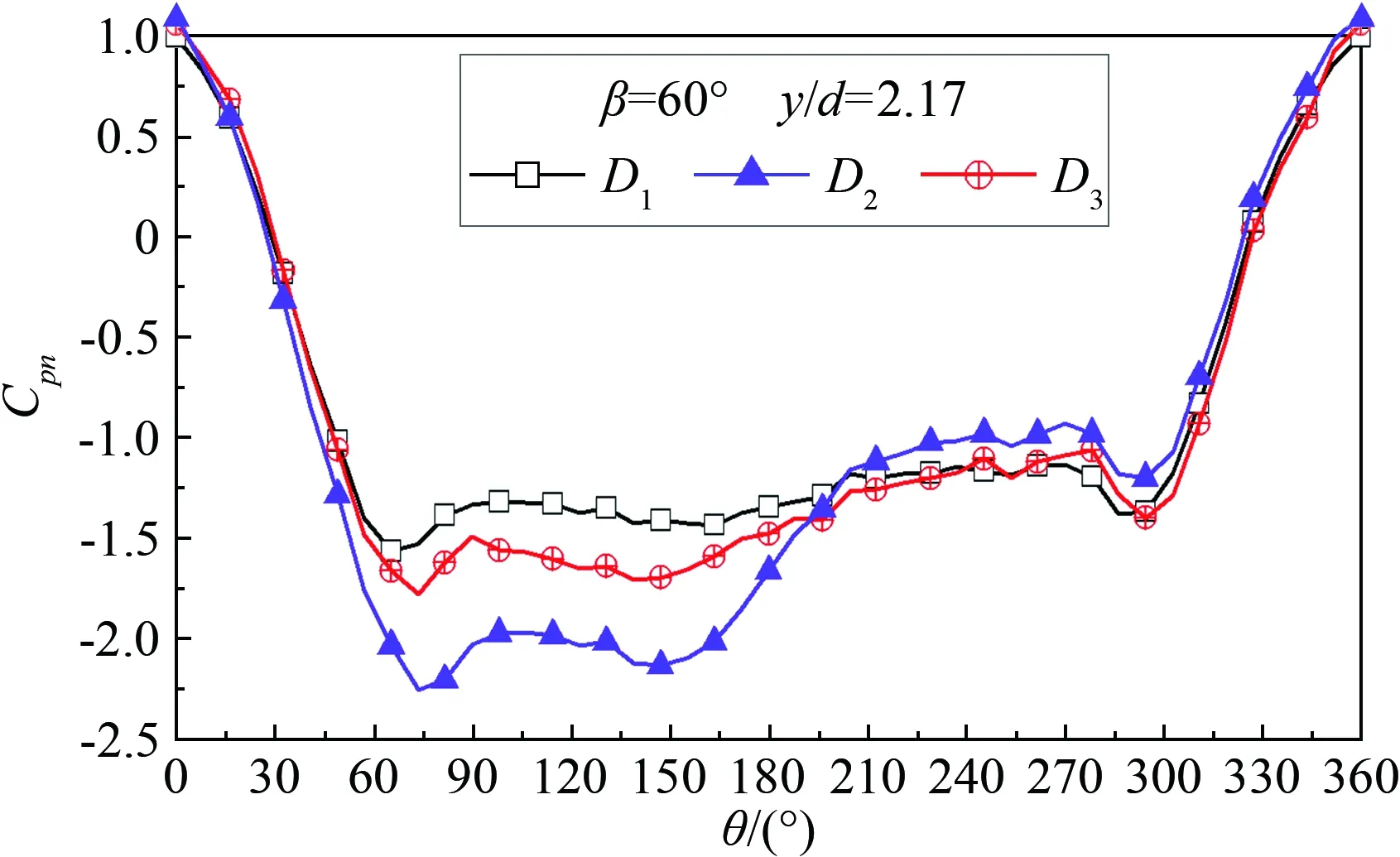
2.4 中间位置(y/d=0.89)挡板对风压分布的影响
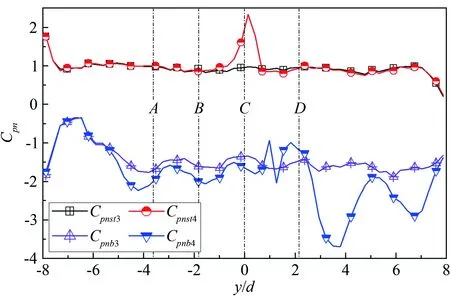

3 结 论

