基于卡尔曼滤波的室内定位方法设计

莫建麟

(阿坝师范学院电子信息与自动化学院，四川汶川 623002)

随着计算机硬件和软件技术的发展，借助GPS设备和全球定位信息系统，室外环境定位效果良好。GPS在移动终端的普及给移动终端带来了很大的便利，方便了人们的生活。而GPS在室内定位却不准确，在某些情况下甚至无法定位。无论是商场导购还是室内救援都需要精准的定位服务。

目前针对室内定位的很多方法均采用无线网络技术、基站定位、惯性定位等多种技术以及将这些技术结合来实现室内人员和物体等位置的监控，并采用一些进化算法、神经网络等方法和支持向量机等方法来进行解决[1-2]。石欣等[3]提出了一种基于改进RSSI的多维标度室内定位算法，基于节点信号建立相异矩阵，并通过多维标度法建立相对坐标，通过平面四参数模型进行坐标转换。李玲霞等[4]提出了一种基于相关性测序的定位算法，利用相邻位置的信号信息构建数据库，然后通过相关性测序算法来实现接收信号参考强度与运动序列之间的匹配。杨明极等[5]提出一种基于主成分分析的聚类算法，对信号强度采用主成分分析法进行白化处理，去除RSSI信息的相关性，以提高定位精度。周瑞等[6]提出了一种基于支持向量机和回归分析法的Wi-Fi指纹定位算法，并采用状态转换方法来识别行走周期并进行计步，以降低惯性传感器的误差和定位误差。刘晓晨等[7]提出了一种基于改进BP网络的室内无线定位方法，以RSSI作为输入，以二维坐标作为输出建立网络，并利用网络的初始化权值和阈值思想进行算法优化，并通过样本数据进行训练。本文提出一种基于RSSI和改进卡尔曼滤波的室内节点定位方法，并通过实验证明该方法的有效性。

1 基于RSSI的室内节点定位

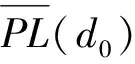
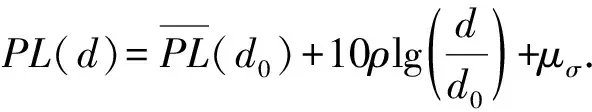
(1)

其中，d0为近地参考距离(取值为1 m)，ρ为信道衰减指数(取值为1～4),μσ为误差项。

在公式(1)建立的模型基础上，接收节点与锚节点之间的距离可以表示为：

(2)

在估计了接收节点和发送节点(锚节点)的距离后，就可以通过极大似然估计法计算接收节点之间的位置。当接收节点接收了n个发送节点的信号，并根据公式(2)估计了与其之间的距离后，由于锚节点位置已知，可以建立具有n个方程的方程组：

(3)

其中，n个发送节点的坐标为(x1,y1),(x2,y2),,(xn,yn)，接收节点的坐标为(x,y)，估计的距离为d1,d2,,dn，公式(3)为非线性方程组。

采用极大似然估计法对AX=B的系数A和B进行估计，可以得到：

(4)

(5)

X=(x,y)T.

(6)

根据公式(6)估计得到的A和B，可以得到估算的值：

X=A-1B.

(7)

2 基于卡尔曼滤波的节点定位

根据式(7)得到的发送节点的坐标仍然不够精确，下面采用基于卡尔曼滤波算法的节点定位方法。

初始化：初始化需要优化的位置X(0),令k+1时刻的网络安全态势预测值为y(k+1)，X(k+1)表示k+1时刻的观测变量，Xi(k+1)(1≤i≤m)为Xi(k+1)的第i个分量，这些因素的个数总计为m，建立回归方程为：

(8)

其中，参数A00,A01,,Amm以及W20,W21,,W2m可以通过式(4)和式(5)来进行估计，得到式(9)：

(9)

其中，

(10)

步骤1 根据式(11)和(12)计算状态方程和预测方程：

X(k+1)=F(k)·X(k)+W1(k).

(11)

y(k+1)=A(k)·X(k+1)+W2(k).

(12)

其中，状态转移矩阵表示为F(k)，状态转移过程中产生的噪声采用W1(k)表示，k时刻的状态向量表示为X(k)=[x1(k),x2(k),,xm(k)]，k+1时刻的状态向量表示为X(k+1)，k时刻的观测噪声表示为W2(k)，k+1时刻的观测向量表示为y(k+1)，A(k)为可以进行观测的观察向量，其中m表示状态向量的维度。

步骤2 建立预测的信息过程：

N(k)=y(k)-A(k)F(k)X1(k-1).

(13)

其中，y(k)的预测值为：

y(k)=A(k)F(k)X1(k-1).

(14)

步骤3 对下列等式进行递归计算：

N(k)=y(k)-A(k)F(k)X1(k-1).

X1(k)=F(k)X1(k-1)-kg(k)N(k).

步骤4 根据式(15)计算发送节点的位置值：

y(k)=A(k-1)X(k).

(15)

3 仿真试验

3.1 实验描述

为了对实验环境进行验证，对图1所示的场景进行分析，该场景包含4条走廊和1个房间，场景包含的区域大小为52×41 m2，参数设置：路径衰减因子ρ为4，近地参考距离为1 m，通信半径为3～15 m，采用文中方法独立仿真20次，并与文献[5]和文献[6]的方法进行比较。

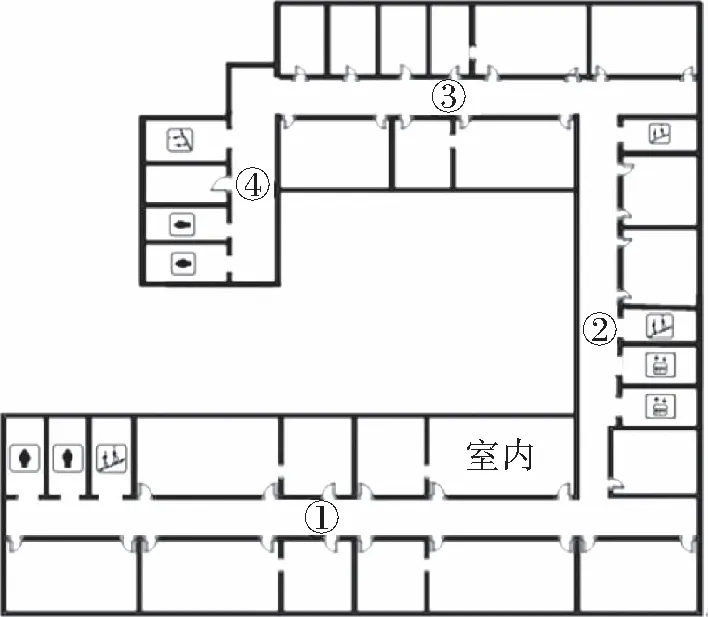
图1 定位场景设置

在图1中，4个位置是锚节点的位置，其它任何节点均可以通过这4个节点的位置，根据本文方法进行定位。算法将从静态情况下的平均定位误差和动态情况下(当在该环境进行行走时，选择不同的情况进行实时定位，这些情况可以分为：短路径(SP)、长路径(LP)、短路径折返(SP-BF)、长路径折返(LP-BF)和室内+走廊(RC))的平均定位误差进行分析。为了进行对比，先对平均定位误差进行定义：

(16)

(17)

其中，R为通信半径。

3.2 待定位节点静止时平均定位误差对比

在待定位节点静态布置的情况下，三种方法随锚节点个数变化得到的平均定位误差,如图2所示。

图2 平均定位误差对比

从图2可以看出，随着锚节点个数的增加，本文方法、文献[5]方法和文献[6]方法均随锚点个数的增加，得到逐渐降低的平均定位误差。其中，文中方法的平均定位误差降得最快，在锚节点个数增加到6时，其对应的平均定位误差为0.07。而文献[5]和文献[6]的方法得到的平均定位误差接近，分别为0.22和0.21。显然，本文方法得到的平均定位误差远远小于文献[5]和文献[6]方法。

3.3 待定位节点移动时的绝对定位误差

由于待定位节点移动时，平均定位误差不断变化。采用绝对定位误差进行比较，不同算法在不同的移动路径情况下，得到的绝对定位误差见表1。

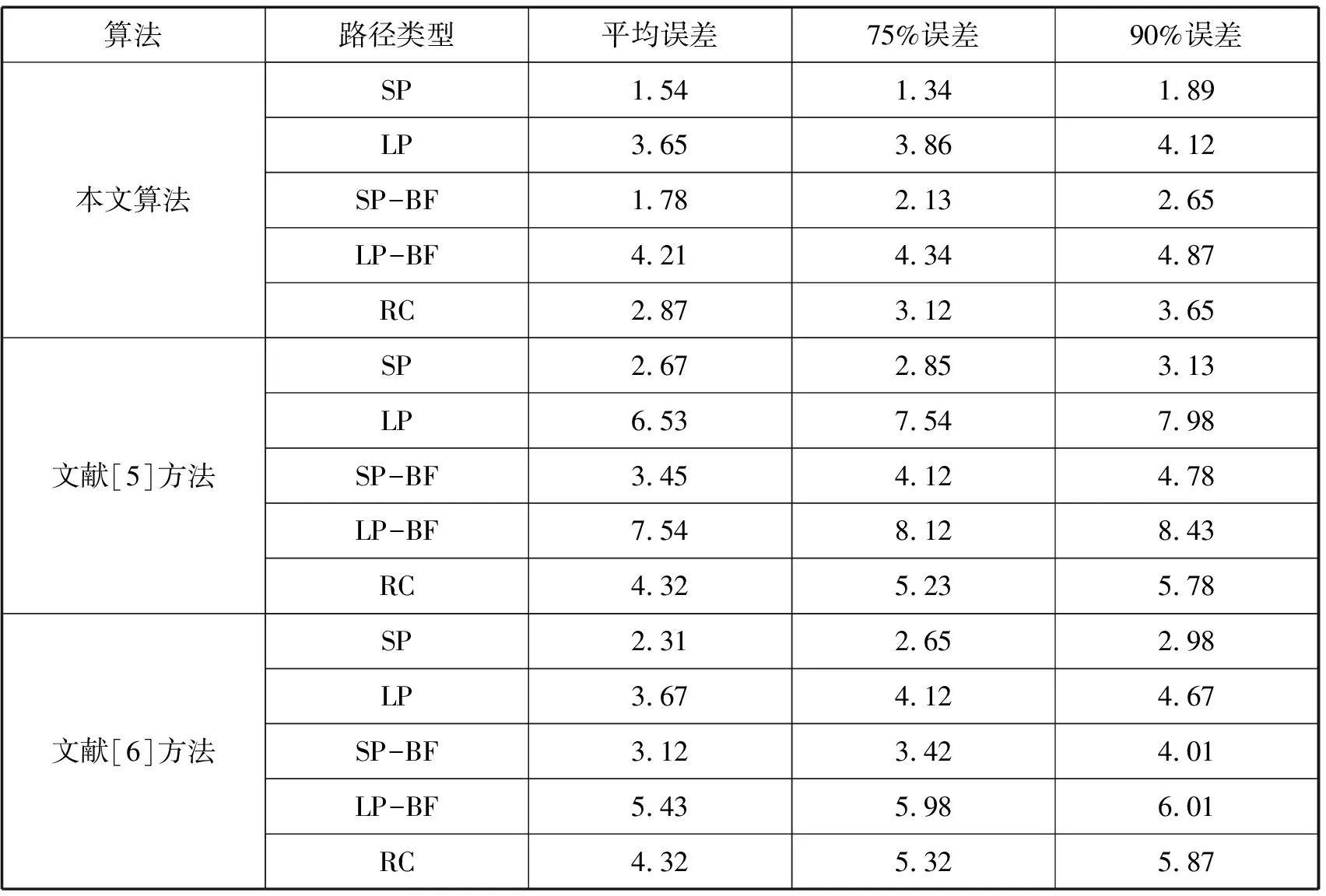
表1 不同算法的绝对定位误差

从表1中可以看出，运用文中方法得到的5种路径定义的平均绝对定位误差均在5 m之内，而75%的定位误差在4.5 m内，而90%的定位误差在5 m内，远远低于另外两种方法，具有较大的优越性。

4 结语

针对传统方法对室内人物和物体定位难度大的问题，本文提出一种基于卡尔曼滤波的室内定位模型。该模型基于RSSI估算待定位节点与发送节点之间的距离，然后通过最小二乘算法来估计位置的初始值。基于估计的初始值，采用卡尔曼滤波算法进一步优化，得到较为精确的预测值。以某室内场景作为仿真环境，对该室内的静止位置和移动目标分别估计平均定位误差和平均绝对定位误差，实验结果表明本文方法在两种情况下均具有较高的定位精度。