Mn掺杂ZnO纳米线磁性质的第一性原理研究

谢建明， 王月影， 陈红霞

(盐城师范学院新能源与电子工程学院， 盐城 224000)

1 引 言

自旋电子学器件要求把磁性材料和非磁性半导体材料结合起来，为此人们把少量的磁性原子掺杂在非磁性的半导体材料中，形成稀磁半导体(DMS)[1]. 由于DMS材料具有磁性和半导体特性，在自旋电子学领域展现出非常广阔的应用前景. 比如自旋阀、自旋二极管、稳定的存储器和逻辑器件等等. 因此，无论在物理上，还是在应用上，稀磁半导体材料都是一个值得深入研究的课题. 一类典型的稀磁半导体是Mn掺杂GaAs，它的居里温度可达到110 K[2]. 考虑到稀磁半导体的商业化应用，则需要将居里温度提高到室温以上.

纤锌矿ZnO是一种宽带隙(室温下为3.37 eV)的半导体材料，激子束缚能高达到60 meV，具有优良光电、压电、压敏、气敏等性质[3]. 理论研究表明，宽带隙半导体可能具有较高的居里温度[4]. 理论和实验上开展了很多关于半导体材料的掺杂研究工作[5-10]. 研究表明掺杂可以显著改变功能材料的各种物性. Zhang等人研究了Gd掺杂ZnO纳米线的磁耦合性质，发现Gd原子处于相邻的位置时，它们之间的相互作用是铁磁性的[11]. Ghosh等人研究了Fe和Co共掺杂ZnO纳米线，发现掺杂纳米线的磁性依赖于Fe和Co的位置[12]. 张等人研究了Cr和Ni掺杂ZnO纳米线的电子结构和磁性质，发现纳米线的磁性依赖于掺杂位置以及纳米线的生长方向[13, 14]. 目前还没有Mn掺杂ZnO纳米线的相关理论研究工作. Mn原子掺杂后会对纳米线的结构和物性产生什么影响，需要进行详细的研究.

本文采用第一性原理方法系统的研究了Mn原子掺杂ZnO纳米线的电子结构和磁性质. 研究结果表明，掺杂提高了纯纳米线的稳定性；所有掺杂纳米线都显示了半导体特性. 纳米线的总磁矩主要来源于Mn原子3d轨道的贡献. 在超原胞内，Mn和O原子磁矩平行排列，表明它们之间是铁磁耦合.

2 计算方法

计算采用了DMol软件包中自旋极化的密度泛函理论. 我们选择了全电子和DND基矢. DIIS方法被用来加速自旋极化自洽场收敛. 交换关联势我们选择了GGA/PBE[15]. 自洽场计算时，总能量的收敛标准为10-6Ha，力的收敛标准0.002 Ha/Å，位置移动收敛标准为0.005 Å. Mulliken布局分析被用来分析电荷转移和原子磁矩[16]. PBE/DND的准确性在前面关于ZnS纳米线和ZnO团簇掺杂磁性质研究工作中已经得到检验[17-21].

3 结果和讨论

纯纳米线是从纤锌矿ZnO体材料中沿[0001]方向切割出来的. 超原胞包含24对Zn、O原子，记作P-ZnO.

我们首先对P-ZnO进行结构优化. 优化后结构显示在图1中. 能带计算结果表明P-ZnO是直接带隙半导体，带隙为1.732 eV. 自旋极化计算表明纯纳米线没有磁性.

图1 纯纳米线和单掺杂纳米线的结构图. 小球代表Zn原子，中等球代表O原子，大球代表Mn原子. Fig. 1 The top views of pristine and monodoped ZnO nanowires . The small, medium, and big balls represent Zn, O, and Mn atoms, respectively.

为了研究掺杂对纳米线结构和物性的影响，我们用一个Mn原子替代纳米线超原胞中的一个Zn原子，对应掺杂浓度为4%. 考虑了两种不同掺杂位置，一种是替代纳米线中间位置的一个Zn原子，另一种是替代纳米线表面位置的一个Zn原子. 分别记作M-ZnO和S-ZnO. 首先对两种掺杂纳米线进行结构优化. 优化后的结果也显示在图1中. 结构优化后，M-ZnO和S-ZnO中Mn-O键的键长分别伸长约0.004 Å和0.009 Å. 表明Mn原子趋于远相邻的O原子.

为了研究掺杂对纳米线稳定性的影响，首先计算了两种掺杂纳米线的束缚能Eb. 定义为Eb=(Etot-EP-EMn+EZn)，其中Etot和Ep分别代表掺杂纳米线和纯纳米线的总能量.EMn和EZn分别代表单个Mn原子和Zn原子的能量. 计算结果列在表1中. 比较发现，两种掺杂纳米线的束缚能都为负值，说明掺杂过程是放热的. 即掺杂增强了纳米线的稳定性. 中间掺杂纳米线束缚能更低，表明Mn原子掺杂ZnO纳米线时，Mn原子趋于占据中间位置. 而在ZnS纳米线中，Mn原子趋于占据表面位置[17].

表1 单掺杂纳米线的束缚能(Eb)，总磁矩(μtot)，Mn原子局域电荷(Q)，局域磁矩(μ)，以及相邻的O原子和Zn原子的磁矩(μO，μZn).

Table 1 The binding energies (Ef, in eV), total magnetic moments (μtot, inμB), local charge (Q, in a.u.), and local magnetic moments (μ, inμB) of Mn atom of monodoped ZnO nanowires. The nearest-neighboring magnetic moments of O atoms and second nearest-neighboring magnetic moments of Zn atoms (μOandμZn, inμB) are also shown.

IsomerEfEgμtotQμμOμZnM-ZnO-2.6720.4784.420.964.590.160.10S-ZnO-2.6450.4634.870.934.61-0.1860.05

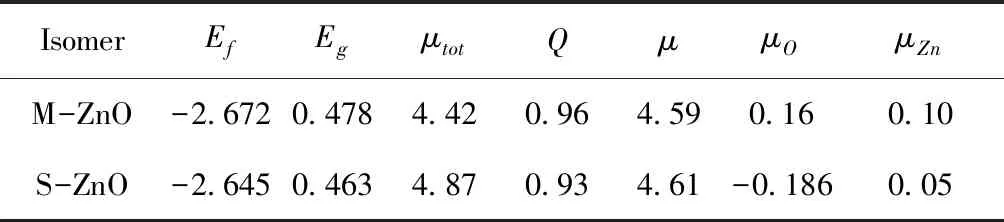
在结构优化的基础上，进一步计算了掺杂纳米线的电子性质和磁性质. 表1列出了掺杂纳米线的能隙. 发现掺杂得纳米线的能隙显著小于纯纳米线的能隙. 为此，图2画出了两种掺杂纳米线的能带图. 发现在纯纳米线的带隙中出现了一些扁平的能带，使得纳米线能隙减小. 对于S-ZnO，导带底和价带顶都在点，显示出直接带隙半导体特性. 而M-ZnO只有导带底在点，显示出间接带隙半导体特性. 而Mn表面掺杂和中间掺杂ZnS纳米线都显示了直接带隙半导体特性[17].

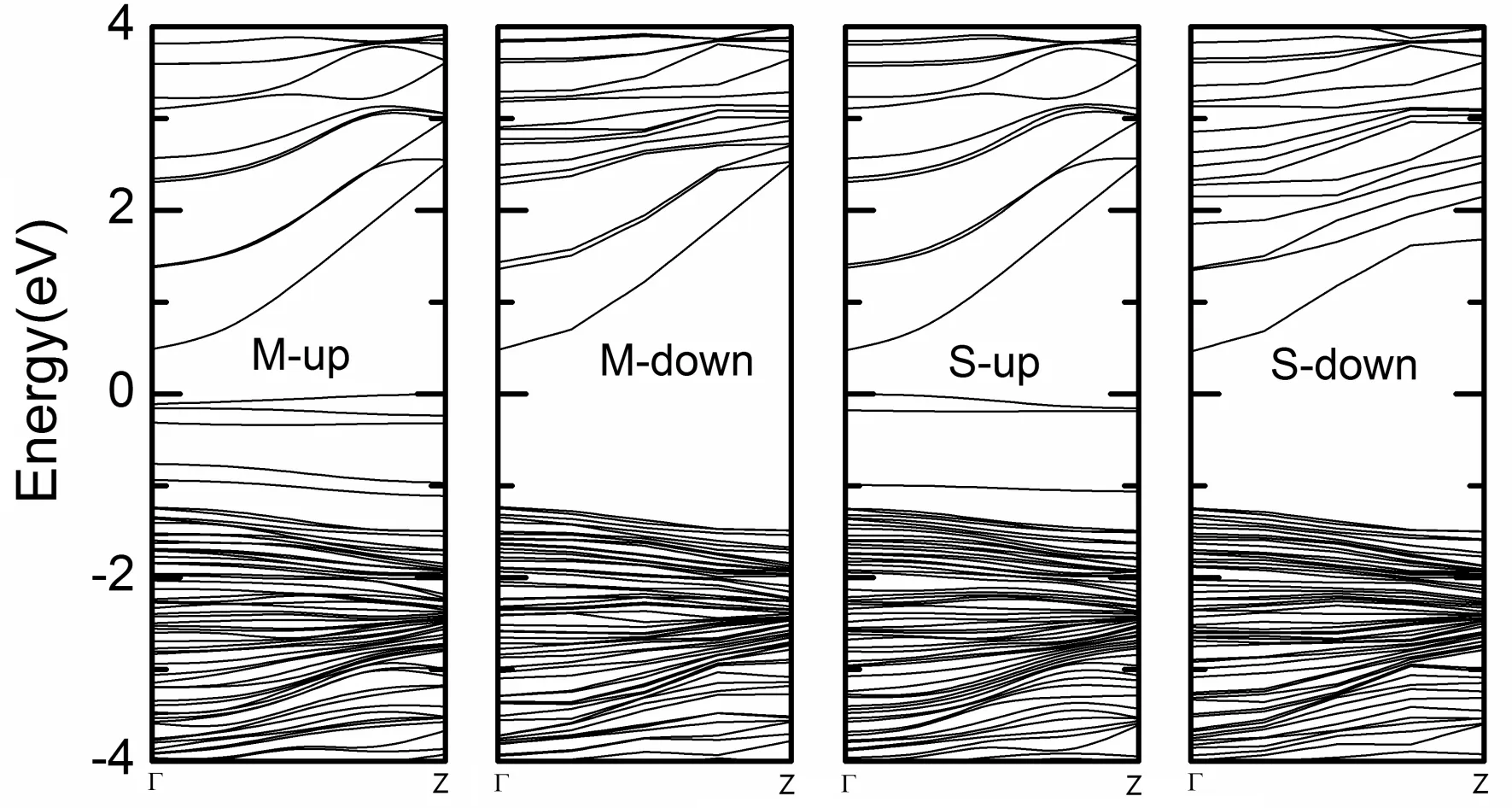
图2 Mn单掺杂ZnO纳米线的能带图. Fig. 2 Electronic band structures for M-ZnO and S-ZnO.

接着，我们计算了两种掺杂纳米线的分波态密度(PDOS). 结果显示在图3中. 从图3可以看出，Mn原子显著改变了费米能级附近的PDOS. 导致了价带顶的自旋极化. 对所有掺杂纳米线，都可以观察到价带顶Mn原子d轨道和O原子p轨道的强杂化. 费米能级附近局域态主要来源于Mn-3d价电子，它在纯纳米线的能隙中引入占据态，导致掺杂纳米线能隙显著减小.

图3 Mn掺杂ZnO纳米线的分波态密度图. Fig. 3 The PDOSs for the M-ZnO (a) and S-ZnO (b).

为了证实PDOS结论，Mulliken布局分析被用来分析电荷转移和原子磁矩. 所有掺杂结构的磁性质也显示在表1中. 掺杂纳米线的总磁矩分别为4.42和4.87μB，是非整数值. 而Mn掺杂ZnS纳米线的总磁矩都等于5μB[17]. 总磁矩主要来源于Mn原子的贡献. 由于杂化，相邻的O原子和Zn原子也贡献了一小部分磁矩. 超原胞中，Mn原子和相邻O原子磁矩方向相同，表明它们之间是铁磁耦合.

最后，为了研究Mn原子间相互作用. 我们用两个Mn原子替代纳米线中两个Zn原子. 共考虑了三种可能的掺杂位置，分别记为MM、MS和SS. 优化后的结果显示在图4中.

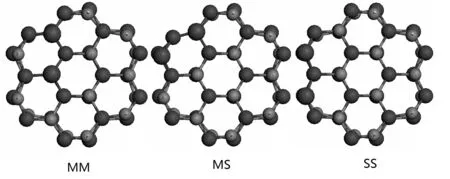
图4 Mn双掺杂ZnO纳米线的结构图. 小球代表Zn原子，中等球代表O原子，大球代表Mn原子. Fig. 4 The top-view maps of Mn-bidoped ZnO nanowires. The small, medium, and big balls represent Zn, O, and Mn atoms, respectively.

为了探究掺杂纳米线的磁性耦合状态，接着计算了双掺杂纳米线中Mn原子间距、束缚能以及铁磁态和反铁磁态的能量差ΔE(ΔE=EFM-EAFM). 结果显示在表2中. 三种掺杂纳米线的束缚能都为负值，表明掺杂增强了纳米线的稳定性. 所有纳米线铁磁态能量都比反铁磁态的能量高，表明Mn掺杂ZnO纳米线磁性耦合状态为反铁磁态. 比较发现，三种掺杂纳米线铁磁态的Mn原子间距都比反铁磁态的Mn原子间距大，表明Mn原子间距越大，体系越不稳定. 其中，MS结构的束缚能最低. 此时，两个Mn原子替代了纳米线表面和中间位置各一个Zn原子. Mn原子间距最小，能量最低. 表明ZnO纳米线可能实现高浓度的Mn掺杂.

Mn原子的局域电荷、局域磁矩以及纳米线总磁矩也列在表2中. 三种掺杂纳米线铁磁态的总磁矩分别为9.86、9.80和9.74μB. 主要来源于两个Mn原子的贡献. 反铁磁态的总磁矩分别为0.11、0.09和0μB. 而Mn掺杂ZnS纳米线铁磁态总磁矩都是10μB；反铁磁态总磁矩都为零[17].

4 结 论

本文采用第一性原理系统地研究了Mn原子掺杂ZnO纳米线的电子性质和磁性质. 所有掺杂纳米线的束缚能都比为负值，说明掺杂增强了纳米线的稳定性. Mn原子趋于占据纳米线的中间位置. S-ZnO显示了直接带隙半导体特性，M-ZnO显示了间接带隙半导体特性. 两种掺杂纳米线的总磁矩分别为4.42和4.87μB. 纳米线的总磁矩主要来源于Mn原子3d轨道的贡献. 由于杂化，相邻的O原子和Zn原子也产生了少量自旋. 在超原胞内，Mn原子和O原子磁矩平行排列，表明它们之间是铁磁耦合. 计算结果表明ZnO纳米线可能实现高浓度的Mn掺杂.

表2 双掺杂纳米线Mn原子间距(d)，束缚能(Eb)，能量差(E)，总磁矩(μtot)，Mn原子局域电荷(Q)，局域磁矩(μ)

Table 2 The distances between twoMn atoms (d, in Å), binding energies (Eb, in eV), energy differences (E, in meV), total magnetic moments (μtot, inμB), local charges (Q, ina.u.), and local magnetic moments (μ, inμB) of Mn atoms in bidoped ZnO nanowires.

铁磁态反铁磁态dEbQμμtotdEbQμμtotDEMM3.47-5.1010.944.720.954.609.863.39-5.1650.93-4.700.954.580.1164MS3.20-5.0640.924.670.964.639.802.88-5.2050.874.490.93-4.550.09141SS3.45-5.0540.924.629.743.40-5.1180.904.60063