螺旋槽干气密封润滑气膜摩擦系数的规律探寻
丁雪兴,徐 洁,张伟政,陆俊杰
(兰州理工大学石油化工学院,甘肃兰州730050)
干气密封是基于无限窄槽理论和气浮轴承原理进行开发的非接触式密封装置,被广泛应用于多个领域的旋转机械轴封[1-3],其中螺旋槽干气密封是最具有代表性的装置,其静环表面光滑,动环表面有螺旋状沟槽且随轴旋转,端面间形成的几微米气膜产生极高的气膜刚度进行密封[4]。在运行过程中,润滑气膜摩擦会使气膜温度升高、温度梯度增大,导致介质泄漏量增大、气膜刚度减小、动静环发生较大热变形[5-6]。随着国家2025智能制造的提出,旋转机械逐渐向高参数工况发展,润滑气膜摩擦影响程度加深,更是对干气密封机组稳定、维护周期、摩擦磨损、能源消耗等提出了巨大的挑战,因此研究润滑气膜摩擦系数有重要意义。
早在1980年,J.Sedy[7]忽略螺旋槽的存在,将动静环简化为一对平行的圆板,通过计算流体内摩擦力得到密封端面间的摩擦力矩;宋鹏云等[8]依据当量间隙近似计算了密封端面间润滑气膜的总摩擦力矩;X.Meng等[9]通过研究流体黏度对微结构平行表面压力分布和承载力的分布,表明了黏性楔形效应对润滑剂的速度分布起着重要作用;S.Blasiak[10]和陈志[11]等分别用传热数学模型和ANSYS Workbench研究了密封环和端面气膜的温度分布,表明气膜产生的剪切热是影响干气密封系统热力分布的关键因素。在数值模拟方面,I.Shahin[12]、丁雪兴等[13-14]利用Gambit软件分析得出干气密封的层流流动模拟与实验结果吻合较好,并得到了压力分布和速度分布及泄漏量;魏龙等[15]通过试验的手段得到了泵用机械密封的端面摩擦因数随介质压力的变化趋势;吴波等[16]研究了不同螺旋槽结构参数对螺旋槽干气密封性能的影响程度,邓成香等[17]进行了计算网格的独立性分析,表明数值模拟结果受到非槽区膜厚网格层数的影响更大。可见,现阶段润滑气膜内摩擦特性的研究较为罕见,且网格划分时大多采用的是传统的Gambit软件,利用高精度网格划分的ICEM软件较为缺乏,而ICEM软件独有的block技术进行结构化网格划分,能很好地贴合几何体,较Gambit生成的网格大大提高了数值模拟精度。
本文采用CFD软件进行模拟计算,改变参数得到压力和速度分布,并利用牛顿内摩擦定律计算,最后分析了润滑气膜摩擦系数的变化规律。
1 数值模拟与计算
1.1 几何模型
结合干气密封系统及动静环的结构特点,建立润滑气膜几何模型,如图1所示。
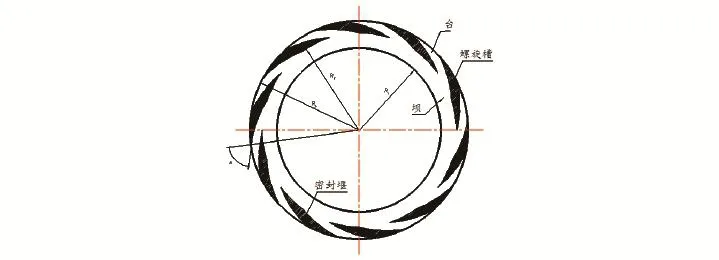
图1 润滑气膜几何模型Fig.1 Geometrical model of lubricating film
本文选取文献R.P.Gabriel[18]中的螺旋槽干气密封端面结构尺寸进行分析,几何参数如表1所示。
1.2 流场的基本假设
做密封端面润滑气膜的稳态分析就是求解雷诺方程以揭示气膜压力的分布规律,因此除等温条件外,推导中还要使用如下假设:
(1)压力在厚度方向保持不变。
(2)密封端面为刚性光滑表面,不考虑粗糙度和变形的影响。
(3)流体为牛顿流体,且不存在涡流和湍流。
(4)气固无界面滑移。
(5)忽略惯性力和体积力的影响。
(6)气体的黏度和密度保持恒定。
(7)动静环对中分布,无偏差或者安装误差。

表1 螺旋槽干气密封的几何参数Table 1 Geometrical parameters of spiral groove dry gas seal
1.3 网格划分
螺旋槽在环形动环上周向均布排列,因此润滑气膜具有对称分布的特点,则可用Solidwoks直接建立1/n润滑气膜模型作为计算域,如图2所示。

图2 润滑气膜的计算模型(轴向放大1 000倍)Fig.2 Calculative model of lubricating film(axial magnifi⁃cation 1 000 times)
划分该模型的网格存在三个难点:一是跨尺度,需要在极薄气膜厚度下保证网格质量;二是不规则模型的复杂性,需考虑计算精度、抗畸变程度以及再次划分等多个因素[19];三是周期边界,划分块时考虑周期边界。图2中periodic-2面为周期边界,网格节点要求一一对应,需将其分割为多个面以达到精度要求。随之进行点、线关联,设置节点数,通过Pre-mesh Quality评价生成的六面体网格质量,满足要求后输出可导入的网格文件。
1.4 网格无关性验证
针对螺旋槽干气密封的气膜计算域模型,分别划分网格数为 13 253、17 238、22 893、26 708,检测模型最高压力值及最高流体速度的大小(见表2)。
由表2可知,网格数量从13 253增加到26 708时,流场的最大压力从669 155.3 Pa变为680 103.4 Pa,增幅为1.64%;流场的最大流速从89.51 m/s变为89.53 m/s,增幅为0.03%。对比可知,在该网格数量变化范围内,流场最大压力和最大流速的变化是很微小的,且当网格数量达到22 893及以上时更加稳定,考虑到数值模拟的计算时间以及减少工作量的要求,故采用网格数目为22 893。
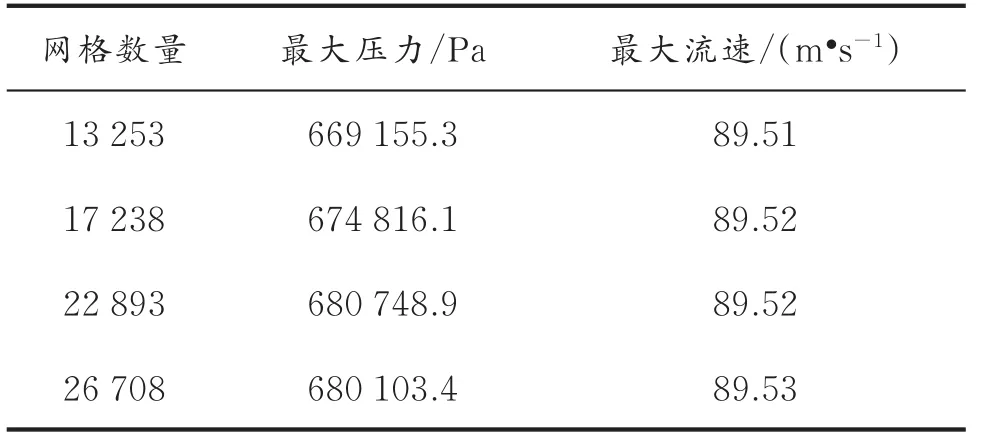
表2 网格无关性验证参数对比Table 2 Comparison of parameters for grid independence verification
1.5 边界条件
采用无滑移边界条件,外半径处为压力入口pressure-inlet,内半径处为压力出口pressure-outlet,动环端面为旋转壁面moving-wall,静环端面为静止面wall。此外两个循环周期边界分别为periodic-1、periodic-2,满足条件:

1.6 输出结果
在Fluent中设置转速为11 000 r/min,入口压力为0.46 MPa,出口压力为标准大气压0.101 325 MPa,密封介质为空气,介质黏度μ为1.8×10-5Pa·s。压力插值采用二阶精度格式,速度耦合采用SIMPLEC算法,开启监视器观察进出口的质量流量的变化、流场的压力以及计算残差,得到流场压力分布云图和速度分布云图如图3所示。
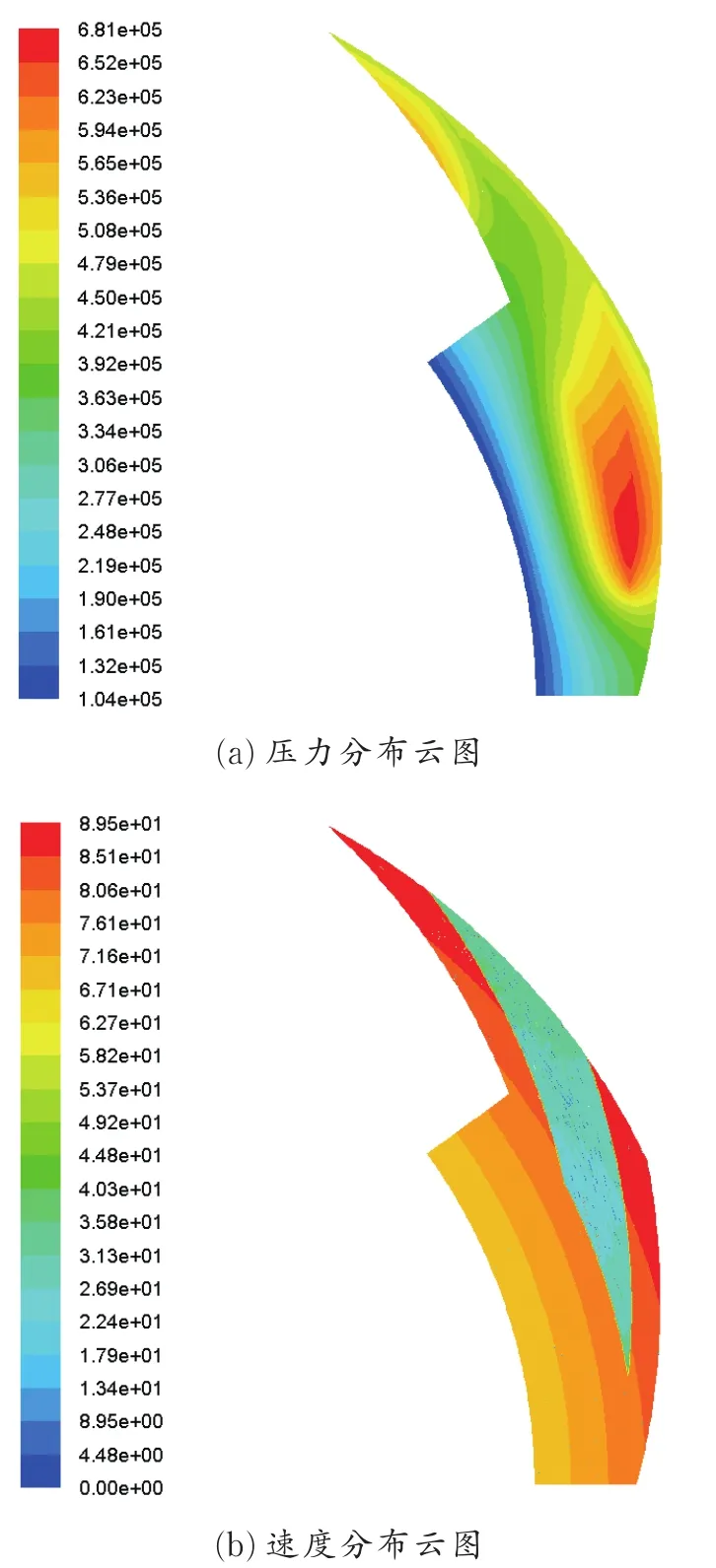
图3 润滑气膜速度和压力分布云图Fig.3 Pressure and velocity distribution of lubricating film
从图3(a)中可以发现,在槽的入口处压力为进口压力,但是随着气体不断深入槽根径的过程中,气体的压力不断升高,说明槽内有泵吸效应和动压效应,同时在槽根径达到了压力的最大值,为0.68 MPa,随后由于槽区与非槽区存在阶梯,发生了台阶效应,对气体流程产生一定的阻力,并有一定的压降,这也是槽根径压力达到最大的另一个原因,最后在槽的内径压力达到了最小值,为0.10 MPa。观察图3(b)可以发现,气膜最大流速可达到89.52 m/s,随着气体从外半径流入内半径,密封环端面间坝区气膜速度是逐渐降低的,槽区气体因膨胀做功速度明显较小。图中的总体趋势可以说明,螺旋槽的存在对气体的流动有巨大影响。
2 润滑气膜摩擦系数的计算
对于常见的气体或液体,满足牛顿内摩擦定律,润滑气膜摩擦力f与气体的动力黏度μ、速度梯度有关:

对式(2)进行化简,
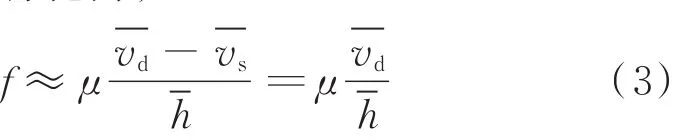
气膜摩擦系数λ与润滑气膜摩擦力f、润滑气膜开启力F有关:

3 参数对润滑气膜摩擦系数的影响
影响润滑气膜摩擦系数的因素有很多,对不同工况参数、结构参数进行数值模拟,得出润滑气膜摩擦系数随不同参数的变化规律。
3.1 工况参数对润滑气膜摩擦系数的影响
3.1.1 转速的影响 转速为3 000~20 000 r/min,介质压力为0.46 MPa,保持槽型结构参数不变,得到润滑气膜摩擦系数随转速的变化规律,结果如图4所示。
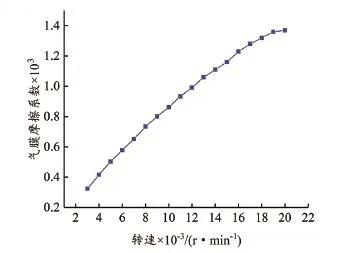
图4 不同转速摩擦系数分布Fig.4 Distribution of fr ictional coefficient to differ ent rotational speed
从图4中可以看出,随着转速增加,润滑气膜摩擦系数增加,最大可达到0.001 4。螺旋槽干气密封润滑层的流动是由压差流和剪切流引起的,如图5所示,压差影响径向速度vr的变化,动环的旋转影响周向速度vθ的变化。一方面,随着转速的增加,周向速度vθ增大,速度梯度增大,另一方面,在转速提高的过程中,槽内压力升高,使压力的波动变大,二者的综合作用使分子动量交换越频繁,流层间制
约越大,所以润滑气膜内摩擦力增大。

图5 润滑气膜的速度示意Fig.5 Speed diagr am of lubricating film
3.1.2 介质压力的影响 介质压力为0.46~0.96 MPa,转速为11 000 r/min,保持槽型结构参数不变,得到润滑气膜摩擦系数随介质压力的变化规律,结果如图6所示。

图6 不同介质压力摩擦系数分布Fig.6 Distribution of frictional coefficient to different medium pressure
从图6中可以看出,随着介质压力增加,润滑气膜摩擦系数减小,且在5 MPa之前降低速度快,在5 MPa之后降低速度缓慢。在该参数下,由于转速、黏度不变,所以润滑气膜摩擦力基本不发生变化。介质压力增大,润滑气膜产生的气膜开启力增大,使气膜摩擦系数降低,但当介质压力增加到5 MPa左右时,润滑气膜摩擦系数变化率明显减小,表明介质压力增加到一定值时,压差流占主导地位,动压效果逐渐达到饱和。
3.1.3 平均气膜厚度的影响 平均气膜厚度为2.55~5.05 μm[20],介 质 压 力 为 0.46 MPa,转 速 为11 000 r/min,保持槽型结构参数不变,得到润滑气膜摩擦系数随平均气膜厚度的变化规律,如图7所示。

图7 不同平均气膜厚度摩擦系数分布Fig.7 Distribution of frictional coefficient to different average gas film thickness
从图7可以看出,随着平均气膜厚度增加,润滑气膜摩擦系数在0.001 3~0.000 8内线性递减。气膜开启力和摩擦力随平均气膜厚度的变化如图8所示,可以看出,随着平均气膜厚度在2.55~5.05μm内增加,气膜开启力从3692.78 N减至2 761.71 N,气膜摩擦力由4.62 N减至2.33 N,二者递减关系均呈非线性,其主要原因为气膜厚度较小时,气膜的剪切率较高。

图8 不同平均气膜厚度气膜开启力和气膜摩擦力分布Fig.8 Distribution of gas film opening force or friction to differ ent aver age gas film thickness
3.2 结构参数对润滑气膜摩擦系数的影响
螺旋槽的存在有利于减小润滑气膜摩擦系数,图9为剪切力分布云图。从图9可以看出,在螺旋槽尖端和非槽区交汇处壁面剪切力增大,物体壁面的突变使得在法向和切向产生力,从而在近运动界面的流层中产生涡量[21],即螺旋槽的存在使流体微团自身发生了旋转在此处产生涡量。一方面,涡量的本质是剪切力,涡量产生的剪切力与动环旋转产生的剪切力相抗衡;另一方面,涡量具有扩散性[22],旋涡强度会在从强度大的地方向强度小的地方扩散的过程中能量耗散,流体速度减小,动量交换减弱,气膜摩擦力减小。

图9 壁面剪切力分布云图Fig.9 Distribution of wall shear str ess
3.2.1 螺旋角的影响 螺旋槽螺旋角为72°~78°,其它槽型结构参数不变,介质压力为0.46 MPa,转速为11 000 r/min,得到润滑气膜摩擦系数随螺旋角的变化规律,结果如图10所示。
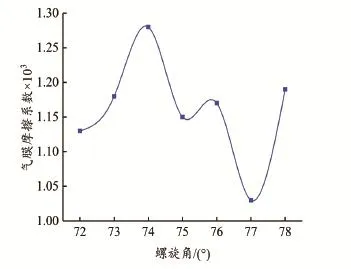
图10 不同螺旋角摩擦系数分布Fig.10 Distribution of friction coefficient to different spiral angle
从图 10中可以看出,在螺旋角为 72°~78°时,润滑气膜摩擦系数变化幅度很小。润滑气膜摩擦系数在螺旋角为74°时有一个波峰,最大值在0.001 28左右,在螺旋角为77°时有一个波谷,最小值在0.001 03左右,但二者的差值只有0.000 25。计算螺旋角在该范围内的润滑气膜摩擦系数的平均值为0.001 16,对应的螺旋角度数为 75°~76°,此时润滑气膜摩擦系数变化较为稳定,可作为今后优化螺旋角的参考。
3.2.2 槽数的影响 螺旋槽槽数为6~12个[20],其它槽型结构参数不变,介质压力为0.46 MPa,转速为11 000 r/min,得到润滑气膜摩擦系数随槽数的变化规律,结果如图11所示。
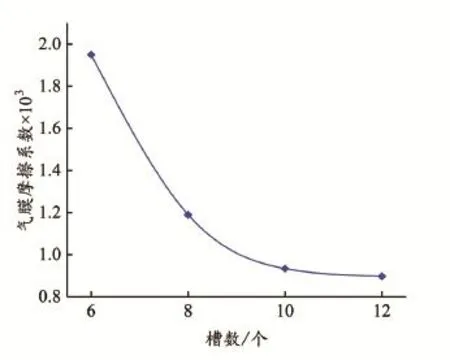
图11 不同螺旋槽槽数摩擦系数分布Fig.11 Distr ibution of frictional coefficient to differ ent number of spiral groove
从图11中可以看出,螺旋槽的槽数增加,润滑气膜摩擦系数减小,可见槽数的增加有利于减小摩擦系数。由图3(b)可看出,流体速度值在螺旋槽根部略微上升,这是因为流体流动到槽根部时受到刚性壁面对流体的反作用力发生了二次流[23⁃24],削弱了主流的速度,抵消了一部分主流黏性剪切力,根据无限多窄槽的原理,槽数增加,二次流的作用将会进一步加强。同时,槽数的增加,可以加强动压效应,提高气膜开启力,降低摩擦系数。但是槽数的变化是有一定的限制范围,从图11中后期趋势变缓可以得知,随着螺旋槽槽数的增加,气膜动压效果增强,润滑层流动状态趋于稳定,润滑气膜摩擦系数变化幅度减小。
3.2.3 槽深的影响 螺旋槽槽深为3.05~11.05 μm,其它槽型结构参数不变,介质压力为0.46 MPa,转速为11 000 r/min,得到润滑气膜摩擦系数随螺旋槽槽深的变化规律,结果如图12所示。
从图12中可以看出,螺旋槽的槽深增大,润滑气膜摩擦系数随之减小,且呈现非线性关系。螺旋槽槽深在3.05~11.05μm逐渐加深,使其有了更加显著的动压效应,从而使开启力随之加大。同时,螺旋槽加深也会使槽区与非槽区的台阶更加明显,台阶效应导致的节流作用也会加强,削弱了一部分速度,最终使润滑气膜摩擦系数降低。
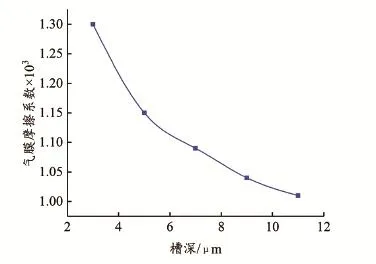
图12 不同槽深摩擦系数分布Fig.12 Distribution of frictional coefficient to different gr oove depth
4 结 论
对螺旋槽干气密封润滑气膜流场进行了数值模拟,并计算分析了润滑气膜摩擦系数的变化规律,得到如下结论:
(1)润滑气膜摩擦系数受转速影响较大,转速增大,润滑气膜速度梯度增大,气膜摩擦系数增大。介质压力增大使气膜开启力增幅明显,气膜摩擦系数降低,但是介质压力增加到一定值时,压差流占主导地位,动压效果逐渐达到饱和,气膜摩擦系数降低趋势平缓。
(2)螺旋槽有利于减小润滑气膜摩擦系数,主要原因是螺旋槽的存在产生了较大动压,气膜开启力增大;其次,二次流及涡流的产生抵消了一部分润滑气膜的摩擦力,同时还存在台阶效应的节流作用。在一定的范围内,螺旋槽越深阶梯效应越显著,产生较大的动压,使得润滑气膜摩擦系数降低。
(3)通过不同槽型参数对润滑气膜摩擦系数的探寻分析可以发现,槽型参数的改变可以在一定程度改变摩擦系数,这为今后槽型与摩擦系数的优化定量分析奠定了基础。

