线型ABC三嵌段共聚物体相结构的模拟

杨婷婷，杨 滢，于 彬

（天津师范大学 物理与材料科学学院，天津 300387）

嵌段共聚物是由2个或2个以上化学性质不同的单体单元构成的聚合物，通过共价键连接而成.嵌段共聚物具有丰富的自组装行为，在光学、电子、化学和生物等领域具有广泛的应用前景[1-3].嵌段共聚物根据组成其单体个数的不同，可分为二嵌段共聚物、三嵌段共聚物和多嵌段共聚物；根据链拓扑结构的不同，可分为线型、星型、梳型、树枝型和环形共聚物等[4].嵌段共聚物通过化学键相连接，由于不同单体的化学性质不同，彼此相互排斥，因此在这种特殊分子结构中会产生微相分离现象，即在10～100 nm尺寸范围产生有序的相结构.嵌段共聚物可作为表面活性剂、热塑弹性体和共混相容剂等，在生物化工、医药和建筑等领域应用广泛[5-6].

AB型双嵌段共聚物是最简单的一种嵌段共聚物，只由A和B两种嵌段构成.近年来，双嵌段共聚物体相的相关研究日趋成熟，在实验和理论研究中得到了相互验证.在AB双嵌段共聚物的溶体状态下，通过改变嵌段的体积分数以及嵌段间的相互作用，观察到了球状相、柱状相、层状相、双连通结构和孔层结构[7-8].在AB嵌段共聚物的稀溶液中，嵌段共聚物的自组装依赖于嵌段的相对长度，从而观察到球状、杆状、层状和双连通结构等大量新奇的形态[9-11].与AB双嵌段共聚物相比，ABC三嵌段共聚物自组装的多样性和复杂性显著提高，因此在结构上会出现了与双嵌段共聚物不同的相图结构[12-15].

三嵌段共聚物的自组装体相主要受体积分数（fA=NA/N，fB=NB/N和fC=1-fA-fB）和分离强度参数χN的影响，其中嵌段A的聚合度NA即嵌段A的链长，嵌段B的聚合度NB即嵌段B的链长，嵌段C的聚合度NC即嵌段C的长度，总聚合度N为共聚物总链长，Flory-Huggins参数χ表示不同单体间相互作用力的大小，主要受温度影响.为了研究线型ABC三嵌段共聚物在三维模拟下自组装的体相，本研究选用Monte Carlo和模拟退火的方法进行计算，通过改变ABC三嵌段共聚物的相互作用力和体积分数，研究不同参数对线型ABC三嵌段共聚物体相的影响.

1 模拟方法与模型

Monte Carlo模拟方法建立在概率论和统计力学的基础上[16]，以随机抽样为主要方法，通过建立概率模型，将其参数设为所求问题的解，然后对模拟过程随机抽样，得到解的近似值，即所求问题的解.本研究采取Monte Carlo模拟方法中的简格子模型对线性ABC三嵌段共聚物的体相进行研究[17-18].模拟过程选取体积为V=Lx Ly Lz（Lx、Ly和Lz为模拟格子3个边的边长）的简立方格子，即3个坐标的方向均采用周期性边界条件[16]实现所需的受限条件.模型中三嵌段共聚物的形式为由此求得各嵌段体积分数为fA=NA/N，fB=NB/N和fC=1-fA-fB.设总链长N=24，NA≤NC，且AA、BB和CC单体间的相互作用力为0，即χAA=χBB=χCC=0.由于采用键长涨落模型[19]，每个单体仅占据1个格点，且任一格点不可被2个及以上单体同时占据，键长为1和计算主要通过链翻转和蛇形运动实现.蛇形运动的具体实现步骤为：随机选取一个空格，并在其周围的18个最近邻位置中随机选取一个嵌段共聚物单体尝试进行交换，如此次交换后与该单体相连的2个键的键长均不超过则该尝试运动被允许；如交换导致与该单体相连的2个键的键长均超过则此次交换被禁止.交换运动最终能否成功还需要由Metropolis抽样原理[20]进一步判断，如交换运动前后的能量差ΔE＜0，则交换运动被接受；反之则此次交换运动以一定概率被接受.

温度的设置采取模拟退火的方法，即Tj=fTj-1，其中Tj为退火到第j步时的温度，f为退火的比例系数.系统的退火过程一直持续到温度达到某个预定值TM为止.模拟中，设定退火步数为70步，即在退火70步时达到预设定的温度值TM.而f的数值取决于相邻两步退火的能量差值，如果能量差值较小，则f=0.92；如果能量差值较大，则f=0.95.一个Monte Carlo步（MCS）定义为所有格点位置都平均历经一次尝试移动，模拟中每个退火步下运行25 000次MCS.

2 结果与讨论

2.1 对称线型ABC三嵌段共聚物的体相

对模拟格子大小V=38×40×42的对称线型ABC三嵌段共聚物进行模拟，设总链长N=24.由于研究对象为对称ABC三嵌段共聚物，故体积分数fA等于体积分数fC，即嵌段A的长度NA等于嵌段C的长度NC，在模拟中设嵌段AB和嵌段BC间相互作用力的大小均为1，即χAB=χBC=1.

嵌段AC间相互作用力的大小χAC分别为1和10时，随着嵌段B长度NB的减小，对称三嵌段共聚物ABC的模拟体相图如图1所示.文中所有图中均由蓝色标注嵌段A，红色标注嵌段B，绿色标注嵌段C.

图1 不同χAC和NB对应的对称ABC嵌段共聚物的模拟体相图Fig.1 Simulated phase structure of symmetric ABC block copolymers with different χAC and NB

由图1可以看出，通过改变χAC以及嵌段A、B和C的体积分数，对称线型ABC三嵌段共聚物的体相呈现不同的形态.当NB=14时，嵌段A与嵌段C组成双连通结构；当NB=12，10和8时，嵌段A、B和C均为周期性排布的层状相，不同的层状所呈现的体相周期不同；当NB=6和4时，嵌段A和嵌段C呈层状相排列，嵌段B呈柱状相排列，形成层中柱的结构.同时，当NB固定时，χAC不同则共聚物的体相也不同.当NB=14时，在不同的相互作用力下，嵌段A和嵌段C虽然同为双连通结构，但当χAC=10时，双连通结构存在一些缺陷；χAC=1时，双连通结构比较完整；当NB=12和8时，嵌段A、B和C均呈周期排布的层状相，但χAC不同时，体相周期大小不同；当NB=6，χAC=10时，共聚物的模拟体相为层状相，而χAC=1时，模拟体相为层中柱结构.

当χAC=1，NB=6和4时，ABC三嵌段共聚物的模拟体相如图2所示，其中图2（a）为NB=6时，模拟体相的正视图，图2（b）为NB=6时，嵌段A和嵌段B的模拟体相图，图2（c）为NB=4的模拟体相图，图2（d）为NB=4时，嵌段A与嵌段B的模拟体相图.

图2 χAC=1，NB=6和4时，对称ABC共聚物及嵌段A和嵌段B的模拟体相图Fig.2 Simulated phase structure of symmetric ABC block copolymers,block A and block B when χAC=1，NB=6 and 4

由图2（b）可以看出，χAC=1，NB=6时，共聚物的模拟体相为层中柱结构，且嵌段B在AC层状相的界面形成了柱状相，而嵌段B形成柱状结构的界面是椭圆形.由图2（c）可知，χAC=1，NB=4时，三嵌段共聚物的模拟体相也出现了类似的层中柱结构，嵌段B形成柱状结构呈现出更加扁平的趋势.通过对比2组层中柱结构，嵌段A、B和C的链长分别为NA=9，NB=6，NC=9和NA=10，NB=4，NC=10时，即嵌段A、B和C的嵌段组分比分别为3∶2∶3和5∶2∶5时，模拟体相呈现层中柱结构，此结果与Stadler工作组的实验结果[21]相符.

χAC=1，NB=12和10时，ABC三嵌段共聚物的层状模拟体相如图3所示，其中图3（a）和图3（c）分别为多周期的层状相，图3（c）和图3（d）为一个周期的模拟体相图.

图3 χAC=1，NB=12和10时，对称ABC共聚物的模拟体相图Fig.3 Simulated phase structure of symmetric ABC block copolymers when χAC=1，NB=12 and 10

当χAB=χBC=χAC=1，NB=8~12时，共聚物表现出多周期层状相（图1）.由图3的（a）和图3（b）可以看出，当NB=12时，嵌段A、B和C均沿简立方格子的z轴方向规则排列，体相周期约为21；当NB=10时，共聚物层状结构的排列与坐标轴存在一定倾角，这是因为模拟盒子的大小和共聚物的体相周期不匹配.通过计算层状结构在3个坐标轴方向的周期数nx、ny和nz，并由估算出体相周期值.当NB=10时，层状相的体相周期约为21.图3（c）和图3（d）为通过改变模拟格子的大小，分别计算出NB=12和10时，嵌段共聚物成单周期层状相，并均沿z方向均匀排布.由图3可知，随着NB的减小，共聚物的体相周期相差不大，均约为21.

改变模拟格子大小V=40×42×44，设总链长N=24，当χAB=χBC=1，χAC=0.1，0和10时，不同NB情况下，对称ABC三嵌段共聚物的体相如图4所示.

图4 改变模拟格子大小后，不同χAC和NB对应的对称ABC嵌段共聚物的模拟体相图Fig.4 Simulated phase structure of symmetric ABC block copolymers with different NB and χAC after changing the volume fraction of each block

由图4可以看出，当χAC=10，NB=14时，嵌段A和嵌段C呈双连通相；NB=12，10和8时，嵌段A、嵌段B和嵌段C均呈层状相，但体相周期各不相同，随着NB的减少，体相周期也逐渐减小；当NB=6时，嵌段B的模拟体相呈现出穿孔层，而嵌段A和嵌段C的模拟体相均呈层状相.χAC=1，NB=14和12时，嵌段A和嵌段C均呈双连通相；NB=10和8时，嵌段A、嵌段B和嵌段C呈层状相；当NB=6时，嵌段B的模拟体相呈柱状相，而嵌段A和嵌段C呈现层状，共聚物的模拟体相呈层中柱相.χAC=0.1，NB=14，12和10时，嵌段B的体相呈层状相，嵌段A和嵌段C平铺在一层呈交错的层状相；当NB=8和6时，嵌段ABC共聚物的体相呈不规则排布.当固定NB=14时，随着χAC的增加，对称ABC三嵌段共聚物的模拟体相由层状相转变为双连通相；固定NB=12，随着χAC的增加，模拟体相由不匀排布的层状相变为双连通结构，再改变成规则排布的层状相；当NB=6时，随着χAC的增加，嵌段共聚物的模拟体相从混乱状态变为层中柱再改变成穿孔层相.由此可知，固定NB时，通过改变χAC，嵌段共聚物的模拟体相和体相周期均发生改变.对比图1和图4可知，在不同模拟格子中，固定χAC=1，当NB=14时，模拟体相均呈双连通结构；当NB=10和8时，三嵌段ABC的模拟体相均呈层状相；当NB=6时，模拟体相为层中柱，由此可知模拟格子大小对三嵌段共聚物体相的影响并不很明显.但当NB=12时，三嵌段共聚物的体相分别为层状相和双连通相，这与计算时选取的随机数以及三嵌段共聚物形成的稳定程度有关.

为了得到更多的有序结构，通过改变模拟格子大小、嵌段AC间相互作用力以及嵌段A、嵌段B和嵌段C的体积分数，计算出嵌段A和嵌段C呈球状和柱状的模拟体相，结果如图5所示.

图5 对称ABC嵌段共聚物形成的双色球和双色柱模拟体相图Fig.5 Two-color ball and two-color column simulated phase structure of symmetric ABC block copolymers

由图5（a）可知，当格子大小V=38×40×42，χAB=χBC=1，χAC=10，NB=20时，嵌段A和嵌段C均呈球状相排布.图5（b）为嵌段A和嵌段C为球形排列的正视图.由图5（b）可以看出，嵌段A和嵌段C所形成的球状相相互交错，均匀地排在简立方格子中.由图5（c）可知，在V=40×40×40模拟格子中，当χAB=χBC=1，χAC=5，NB=18时，嵌段A和嵌段C呈柱状均匀排布，而嵌段B以穿孔层的形式排列在简立方格子中.图5（d）为嵌段A和嵌段C呈柱状均匀排布的正视图.由图5（d）中可以看出，嵌段A和嵌段C形成的柱状相相互交错排布在简立方格子中，并沿着坐标轴方向均匀排布.由图5可知，在不同参数作用下，对称三嵌段ABC共聚物的模拟体相会出现嵌段A和嵌段C呈双色球和双色柱的对称结构.

2.2 非对称ABC三嵌段共聚物的体相模拟

固定非对称ABC三嵌段共聚物的大小V=40×40×40，设总链长N=24，且NA＜NC，即fA＜fC，同时χAB=χBC=1.

当NB=4，χAC=0.1、1和10时，通过改变嵌段A的长度得到非对称三嵌段共聚物的模拟体相如图6所示.

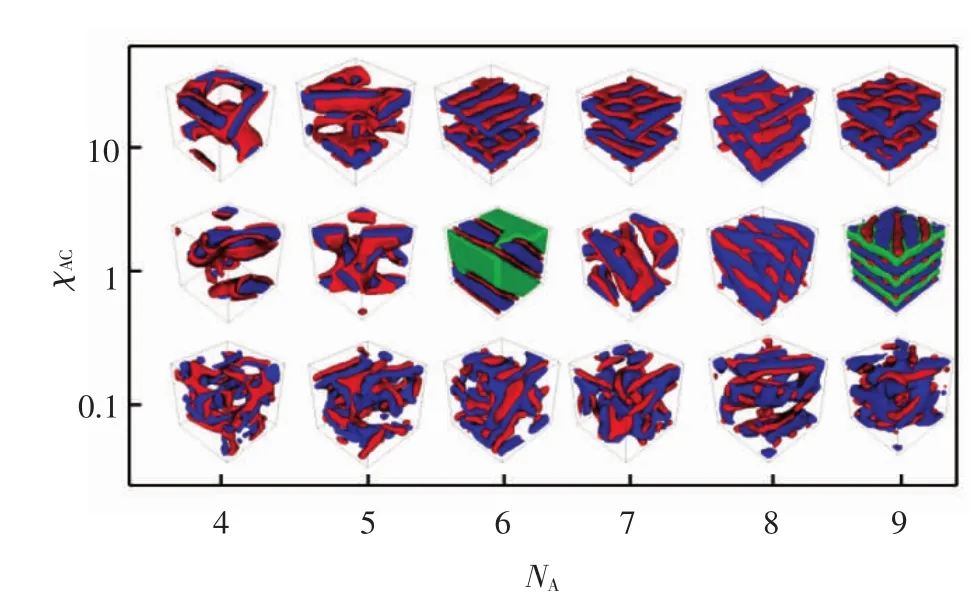
图6 当NB=4时，不同χAC和NA对应的非对称ABC共聚物的模拟体相图Fig.6 Simulated phase structure of asymmetric ABC block copolymer with different χAC and NA when NB is 4

由图6可知，χBC=0.1时，随着NA的增加，ABC三嵌段共聚物获得的自组装体相呈混乱的状态，无有序体相形成，这与实验结果以及其他模拟方法计算出的结果相同[22-24].在χBC=1的情况下，当NA=6，NC=14（即A6B4C14）时，嵌段A和嵌段B形成穿孔层结构，其他部分由嵌段C进行填充；当NA=7，NC=13时，嵌段A形成柱状，而嵌段B呈空心柱，并附着在嵌段A共聚物的表面，其他部分由嵌段C共聚物填充；当NA=8，NC=12时，嵌段B形成柱状相排列，而嵌段A和嵌段C形成层状相；当NA=9，NC=11时，嵌段B同样形成柱状相，嵌段A与嵌段C则呈层状相，且ABC三嵌段共聚物在简立方格子中呈现周期排布.在χBC=10的情况下，当NA=4，NC=16时，嵌段A和嵌段B均成穿孔层排布，且呈空心穿孔层状的嵌段B附着在嵌段A表面，其他部分由嵌段C填充；当NA=6，7，8和9时，嵌段B的体相均呈穿孔层排布，而嵌段A和嵌段C的体相均以层状排布，且在不同体积分数下，嵌段共聚物的体相周期不同.

当NB=7，χAC=0.1，1和10时，改变NA得到ABC三嵌段共聚物的模拟体相如图7所示.由图7可知，当χBC=0.1时，随着NA的增加，ABC三嵌段共聚物呈现不规则的混乱相排布.在χBC=1的情况下，当NA=4，NC=13时，嵌段A呈连通相，嵌段B附着在嵌段A表面形成空心结构，其他部分由嵌段C进行填充；当NA=6，7和8时，共聚物的体相均呈层状相排布.且当χBC=7时，嵌段ABC共聚物的体相呈均匀排布的层状相.在χBC=10的情况下，当NA=4，5和6时，嵌段B的体相呈穿孔层，嵌段A和嵌段C分别呈层状相排布；当NB=7和8时，嵌段A、嵌段B和嵌段C均呈层状排布.

图7 当NB=7时，不同χAC和NA对应的非对称ABC共聚物的模拟体相图Fig.7 Simulated phase structure of asymmetric ABC block copolymer with different χAC and NA when NB is 7

实验和理论研究中已找到了多种有序结构，例如，杨玉良等[16]应用SCFT方法确认得到了层状相、六角柱、核-壳型柱结构、含有内嵌球或界面球的层结构以及包含界面球的柱状结构等稳定形态.Zheng等[25]通过联合Ohta-Kawasaki自由能表达和DFT方法，确认了11个形态.Shefelbine等[26]在对非对称三嵌段共聚物isoprene-b-styrene-b-dimethylsiloxane熔体的研究中发现了核-壳型的gyroid形态，这一结构同时也被Hückstädt[27]在对styrene-b-1，2-butadiene-b-2-vinylpyridine三嵌段共聚物的研究中确认.而本研究通过计算方法，仅验证得到了ABC三嵌物的层状相、层柱状相、界面球状相和穿孔层状相，这是由于模拟格子大小的选取以及嵌段间结构的复杂性造成计算时间的延长，因此获取的有序结构较少.

3 结论

本研究采用模拟退火方法对熔体下线型ABC三嵌段共聚物的自组装行为进行模拟.运用Monte Carlo模拟方法，通过调整简单立方格子大小、嵌段A与嵌段C间的相互作用参数以及嵌段A、嵌段B和嵌段C的长度，获得了多种微观有序结构，并将这些结构与已有的实验和结论结果进行比较，得到以下结论：

（1）在对称三嵌段共聚物中，随着B嵌段长度的减小，对称线型ABC三嵌段共聚物的体相依次形成了双连通结构、层状相和层柱状相.

（2）在对称线型ABC三嵌段共聚物中，当B嵌段的长度为8~12，三嵌段共聚物的模拟体相呈层状结构，且当嵌段AC间相互作用相同时，层状结构的体相周期均约为21.

（3）在非对称线型ABC三嵌段共聚物中，当嵌段AC间相互作用较弱时，三嵌段共聚物的模拟体相结构呈无序排布；随着嵌段AC间相互作用逐渐增加，三嵌段共聚物的模拟体相出现有序结构，如层状结构、穿孔层结构和层中柱结构.