公路隧道二次衬砌钢筋环向间距对结构安全性影响分析

秦之富，王世伟，刘文斌，周 雄，秦武军

(1.招商局重庆交通科研设计院有限公司， 重庆 400067； 2.交通运输部路网监测与应急处置中心， 北京 100000)

新版《公路工程质量检验评定标准 第一册 土建部分》(2017)隧道部分规定衬砌主筋间距偏差为±10 mm，由于隧道内施工环境恶劣，一线施工人员很难合规地完成现场钢筋绑扎、浇筑。目前，有学者就钢筋间距对结构的影响做了一些研究。何明峰[1]采用荷载-结构模型对实测的铁路隧道进行了承载力结构验算，证明了既定工况下隧道钢筋间距超标时结构安全系数。王长海[2]依托工程实例分析了钢筋间距过大对过水闸墩单孔的影响。其他研究者则多采用二维数值模拟方法判定结构的安全系数，从而进行结构安全预测分析。

然而，在以往的钢筋间距受力影响的研究中，多考虑了隧道整体的安全性，对钢筋间距变化引起钢筋受力形态的影响特性研究较少，而详细掌握钢筋受力形态对控制现场工程质量极为重要。因此，本文结合工程案例，采用数值模拟方法，对二次衬砌配筋间距进行独立分析，研究在钢筋环向间距变化的情况下衬砌内力的变化规律及特点，以期为隧道施工质量控制提供支持[3]。

1 工程概况

某公路隧道上覆第四系松散残坡积层，厚度较薄；洞身段地势高，山坡坡度较陡，局部基岩裸露，植被较发育。隧址区地貌单元属高山区。该隧道采用台阶法开挖，复合式衬砌，隧道V级围岩下二次衬砌的支护设计参数如表1所示。

表1 二次衬砌设计参数

2 隧道衬砌的数值模拟

为了研究钢筋间距变化对衬砌结构受力变化的规律及特点，将既定工况下按照Va支护的二次衬砌作为研究对象，不建立土体三维模型，将围岩作用力施加在二次衬砌结构外表面，分别建立不同环向钢筋间距下结构的计算模型。

2.1 计算模型的建立

根据设计资料，采用ABAQUS有限元分析软件建立二次衬砌分析模型，混凝土采用C25普通混凝土，环向钢筋为HRB335，二次衬砌模型轴向长度为10 m，厚度为50 cm，钢筋采用各向同性的弹性模型，二次衬砌采用弹塑性模型，混凝土的应力-应变关系采用双参数模型，混凝土采用CPE4单元，环向钢筋采用线性杆单元T3D2。本文主要研究二次衬砌内环向钢筋间距变化引起的结构受力变化，因此只建立二次衬砌中的环向钢筋，不考虑二次衬砌的纵向钢筋及箍筋[4]，隧道衬砌支护设计如图1所示，有限元计算模型如图2所示，二次衬砌结构主要材料参数如表2所示。

图1 隧道衬砌支护设计Fig.1 Design drawing of tunnel lining support

图2 有限元计算模型Fig.2 Finite element model

表2 二次衬砌材料参数

依据二次衬砌结构形式，在二次衬砌配筋率不变的情况下，分别取二次衬砌内部环向钢筋间距的误差为0、±30 mm、±50 mm，并将其随机布置(随机数由软件自动生成)。模型前后约束轴向方向的位移，底部约束X、Y和Z轴方向的位移，二次衬砌外表面采用地基弹簧进行约束，隧道内为自由面，衬砌结构中心线对称位置处限制左右位移和转角变形，选取V级围岩时的深埋隧道作为荷载计算工况，将已建立好的模型进行网格划分，并进行计算，边界条件及荷载作用方式如图3所示。

图3 边界条件及荷载作用方式

2.2 隧道二次衬砌加载

本次分析着重考虑钢筋间距变化时，衬砌结构内部应力的变化情况。为了便于对比分析计算结果，数值模拟过程中采用JTG D70—2004《公路隧道设计规范》[5](简称《规范》)的计算公式施加围岩压力，不考虑所处地质情况下岩体产生的构造应力。

依据《规范》[5]，围岩垂直竖向荷载计算公式为

q=γh

(1)

h=0.45×2s-1ω

(2)

式中：γ为围岩容重，kN/m3；q为垂直竖向压力，kN/m3；h为荷载等效高度，m；s为围岩级别；ω为宽度影响系数，ω=1+i(B-5),其中i为B每增减1 m时围岩压力增减率，以B=5 m的隧道围岩垂直竖向均布压力为准，当B<5 m时，取i=0.2；当B>5 m时，取i=0.1。

依据《规范》，二次衬砌受力由竖向荷载和水平荷载组成，其中竖向荷载由公式求得，水平荷载考虑无构造应力状态下的侧压力q水=λq，其中在V级围岩的情况下λ=0.3～0.5。

弹塑性计算时，为便于结果对比，依据《规范》中二次衬砌荷载作用方式，结合隧道实际工况，此时围岩压力按《规范》计算法则进行考虑，作用形式为垂直竖向荷载与侧向土压力荷载叠加考虑，并将围岩压力按照70%进行折减，然后作用在二次衬砌上，同时考虑二次衬砌混凝土及钢筋的自重应力。

3 数值模拟及其结果分析

利用已建立的隧道二次衬砌计算模型和相关荷载参数，对隧道二次衬砌有限元模型进行弹塑性静力计算分析[6-9]，并对计算结果进行如下分析。

3.1 隧道二次衬砌结构分析

在二次衬砌配筋率不变的情况下，分别按照设计间距、间距随机偏差±30 mm、间距随机偏差±50 mm三种配筋形式下的二次衬砌结构进行数值模拟分析，分别得出3种钢筋间距下的衬砌结构应力云图，如图4～图6所示。

图4 设计间距下衬砌应力云图Fig.4 Stress of lining under design spacing

图5 间距±30 mm下衬砌应力云图

图6 间距±50 mm下衬砌应力云图

由图4～图6可知：

1) 在同种加载方式及约束条件下，3种工况下二次衬砌应力集中的位置不随钢筋间距的变化而发生较大的变化，但在隧道拱腰及拱脚处均有明显的应力集中现象，其中以拱腰、拱脚处应力集中尤为突出。随着钢筋间距的改变衬砌结构整体应力变化不大，其中当钢筋间距偏差±30 mm时，混凝土最大应力是设计间距下的3.66倍；当钢筋间距偏差±50 mm时，混凝土最大应力是设计间距下的3.64倍。由此可见，±50 mm以内钢筋间距的变化对二次衬砌整体结构受力影响不显著，但在衬砌结构某些位置处发生应力集中。

2) 若考虑二次衬砌结构在侧压力作用下结构的受力情况，实际工程中往往在构造应力的作用下，围岩的侧压力通常会大于竖向压力。在竖向压力和侧压力的共同作用下，根据图5和图6所示，二次衬砌自由面可能产生拉应力，概率较大的位置发生在拱腰和拱顶处，但其他部位也会产生拉应力，在二次衬砌边墙处通常为应力反弯点，此时拱脚的墙背处将产生拉应力。据上分析可知，当二次衬砌配有2层钢筋时，施工质量检查尤其要注意拱脚内侧钢筋以及拱腰外侧钢筋的布设情况。

3.2 隧道二次衬砌钢筋应力分析

在钢筋不发生滑移变形的情况下，二次衬砌内部钢筋与混凝土协同变形[10-12]，二次衬砌的宏观应力变化直接反映钢筋的应力变化，分别提取3种钢筋间距下的二次衬砌钢筋应力云图，如图7～图9所示。

分析图7～图9可知：

1) 弹塑性计算时，二次衬砌钢筋应力集中的位置基本一致，均表现为拱腰内侧钢筋以及拱脚拱背处钢筋应力集中，其中以拱脚的拱背处应力集中现象最为突出，此时钢筋拉应力最大。随着钢筋间距的变化，衬砌结构整体应力变化不是很明显，其中当钢筋间距偏差±30 mm时，混凝土最大应力是设计间距下的5.08倍；当钢筋间距偏差±50 mm时，混凝土最大应力是设计间距下的5.78倍。与衬砌结构相比钢筋内部应力集中现象更加显著，由此可见钢筋间距的变化对钢筋本身的应力影响较大。

图7 设计间距下钢筋应力云图Fig.7 Stress of steel bar under design spacing

图8 间距±30 mm下钢筋应力云图

图9 间距±50 mm下钢筋应力云图

2) 提取3种工况下二次衬砌同一位置处的整圈钢筋应力分布，然后对比分析3种工况下的应力，结果如图10所示。

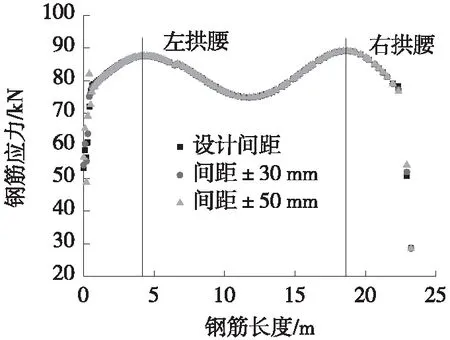
图10 3种工况下钢筋应力曲线Fig.10 Stress curves of reinforcement bars under three working conditions

由于仰拱不是本次分析的重点，分析时只考虑仰拱上部结构。通过对比钢筋应力值曲线的分析结果可知，钢筋应力在拱腰处达到最大，拱顶处应力有所下降，整条钢筋呈现”驼峰”曲线[7]。此外，在拱脚处钢筋应力剧烈变化，并随钢筋分布间距的变大，应力集中的峰值应力值越大，随着提取点逐渐远离钢筋拱脚位置，应力集中现象越来越弱，当达到边墙位置时，应力集中现象几乎消失，整个应力曲线图近似对称，同理可知对边应力分布规律。

3) 将3种工况下的数据进行处理，公式如下：

ηd=[(fd-f设计)/f设计]×100

(4)

式中：ηd为应力系数(与设计值相比的百分值)；d为不同钢筋间距，m；f为应力值，MPa。

按照上述公式，将整根钢筋不同位置处的应力值与原设计工况下的应力值进行比较，如图11所示。与上述应力分析结果基本吻合，靠近拱脚处钢筋应力变化剧烈，钢筋间距为±30 mm时比±50 mm时的变化率要小。钢筋间距为±30 mm时，最大应力集中偏差率为4.4%；钢筋间距为±50 mm时，最大应力集中偏差率为14.0%，且最大应力集中偏差率发生的位置均在拱脚附近。由此可见，钢筋间距的不均匀布设对钢筋应力集中有较大的影响，在偏差为±30 mm时，偏差值相对较小，为可接受偏差率；钢筋间距在此基础上增加20 mm后钢筋的应力集中率出现陡增，为不可接受的偏差率。

图11 钢筋应力集中百分比

4) 综上分析，钢筋的间距偏差主要影响钢筋及其周边裹挟的混凝土，主要体现在拱脚应力集中。随着远离拱脚，应力集中现象减弱，在高于边墙位置时应力集中现象几乎可以消除；此外，拱脚墙背处钢筋受拉应力，根据应力曲线反映的结果，钢筋间距偏差值为±50 mm应力偏差值较大，不利于拱脚位置处钢筋受力；尽管拱脚处应力集中现象明显，但在拱腰处整根钢筋应力值最大，且拱腰位置应力曲线分布呈“驼峰”形式。

4 结束语

1) 在配筋率不变的情况下，二次衬砌钢筋间距的变化对衬砌结构受力影响较小。二次衬砌受力薄弱位置仍然是拱顶、拱腰、拱脚位置，影响主要体现在衬砌表面应力最大值发生变化，反映到实际工程中，结构表层混凝土因应力集中而产生开裂或表层脱落。

2) 通过对比钢筋间距变化引起的结构内力响应，当钢筋间距在±30 mm以内变化时，二次衬砌应力集中现象较弱，此时应力集中最大增幅为5.6倍，当钢筋间距在±30 mm～±50 mm变化时，结构应力陡增到设计间距的14倍，表现为结构应力集中位置处混凝土开裂剥落，随着使用环境的变化，二次衬砌将发生不同程度的裂损，进而影响二次衬砌的耐久性和运营安全。

3) 依据结构计算结论，在隧道施工过程中应力集中现象多发生在隧道拱脚处，但实际工程中拱脚常作为钢筋搭接的位置，若施工质量欠佳将削弱结构的承载力，因此在隧道二次衬砌施工质量控制中，不仅要管控混凝土质量和钢筋强度，还要严格把控拱脚处钢筋绑扎搭接质量，从而增强结构整体受力，更好地消除应力集中。

4) 《公路工程质量检验评定标准 第一册 土建部分》对二次衬砌钢筋间距的偏差作了严格的规定，基于上述计算分析对于施工条件艰苦的高寒地区，在不影响结构整体承载的情况下，通过结构评估可以适当将钢筋间距误差放宽至±30 mm。