基于特质波动率的投资组合研究

段潇儒 郑 旭

（上海交通大学 安泰经济与管理学院，上海 200030）

风险与收益之间的关系一直是金融学研究的重要内容。理论上，经典的资本资产定价模型（CAPM）指出，由于投资者都持有充分分散的投资组合，风险资产的预期收益只与该资产所承担的系统性风险有关，其特质风险不影响均衡价格。而根据Miller，存在卖空限制的情况下，投资者的异质信念会导致证券被系统性地高估，因为此时股票定价由市场上最乐观的投资者进行，悲观投资者的情绪无法体现在市场上，而过高的定价最终会回落，这就意味着异质信念与风险调整后的收益率成反比。Merton提出了投资者认知假说（IRH），认为由于所掌握的信息不完全，投资者只持有自己熟悉（了解风险和收益特征）的证券，在持有的组合未能完全分散的条件下达到均衡时，证券的预期收益率与特质报波动率成正比。

实证研究中，Ang等使用美国市场从1963年到2000年的股票数据，首次对公司层面的特质波动率进行了研究，以每月中的日频数据进行Fama-French三因子回归，用残差的标准差度量特质波动率，发现股票特质波动率与横截面预期收益显著负相关，并且该现象不能由规模、账面市值比、杠杆、流动性、成交量、换手率、买卖价差、协偏度、分析师预测分歧程度、动量等因素解释。Ang等扩大样本范围，对23个发达国家市场进行检验，发现这一现象依旧显著。表征异质信念的分析师预测分歧度无法解释这一现象，意味着与Miller的理论不符，而负相关关系又与Merton的理论预测相悖，Ang等将这一异象称为“特质波动率之谜”。

针对“特质波动率之谜”，国外的研究进行了不同的解释。Jiang发现信息披露质量可以在很大程度上解释特质波动率对收益率的预测效力，因为通常更少的信息披露会导致投资者之间的异质信念，从而增加股票的波动率，而信息披露越少，未来的预期收益越低，这支持了Miller的理论。Boehme等认为Merton和Miller的理论不冲突，前者是针对低“可见性”的股票，而后者对“可见性”则没有要求，用前52周周超额收益率的标准差度量特质波动率，以机构持股度量“可见性”，在低“可见性”的股票范围中，控制相对卖空比例，发现股票的特质波动率和预期收益显著正相关，符合Merton的理论。Bali等则认为Ang等的结论并不稳健，使用月频数据而非月内日频数据估计特质波动率，使用市值加权法而非等权法构造投资组合，以及使用不同的方法分组，都会影响特质波动率与截面预期收益率之间负相关的存在性和显著性。Fu检验了特质波动率的时间序列特性，发现滞后一期的特质波动率不能很好地估计下一期的特质波动率，而使用EGARCH模型估计的预期特质波动率，与期望收益率存在显著的正相关关系；Fu还发现Ang等的结果在很大程度上受到了一部分高特质波动率的小公司的影响，这些公司在特质波动率高的月份的收益率相对更高，而在随后的月份中则出现了负的超额收益。Huang等同样发现控制了短期的反转效应之后，特质波动率与预期收益率之间的显著负相关关系消失了。

国内不少的研究发现A股市场存在特质波动率异象。杨华蔚等沿用Ang的方法估计特质波动率，发现中国市场中，股票特质波动率与横截面收益率存在显著的负相关关系，但与成熟市场不同，特质波动率的异常收益在小规模公司和大规模公司股票中都存在，并且换手率可以部分解释这种负相关，他们将此解释为市场存在的大量散户投资者和卖空机制的缺失等交易者结构与制度限制所致。左浩苗等研究国内股票市场，同样发现特质波动率越高，横截面收益率越低，并且这种负相关关系与特质波动率的估计方法（GARCH、EGARCH、ARIMA模型一步向前预测的特质波动率）和组合加权方式都无关，但在控制了表征异质信念的换手率后，这种负相关关系消失了，他们将此解释为卖空限制和投资者异质信念共同作用，导致资产被高估从而降低未来的收益率。刘维奇等、虞文微等对A股市场的研究同样肯定了“特质波动率之谜”的存在，前者发现价格极差可以在一定程度上解释但不能完全解释“特质波动率之谜”，后者发现卖空机制的引入能够降低异质信念的程度，减弱特质波动率异象。

也有研究得到了不同的结论。邓雪春、郑振龙发现使用ARMA模型估计得到的预期特质波动率与预期收益率之间存在显著的正向关系，并且这种关系在考虑了各种控制变量之后依然成立。田益祥、刘鹏发现使用EGARCH（1，1）模型估计得到的预期特质波动率与股票收益率存在显著的正相关关系，同时机构投资者持股比例越低的股票，特质风险越大，股票预期收益越高。李竹薇等基于HP滤波法将特质波动率分解为长期特质波动率和短期特质波动率两部分，分别研究二者与股票截面收益之间的关系，发现长期特质波动率与股票截面收益成正向关系，短期特质波动率与股票截面收益成反向关系。罗登跃基于Fama-French规模-账面市值比5×5组合对特质波动率与横截面收益的关系进行检验，发现当期已实现特质波动率和非预期特质波动率均与收益显著正相关，滞后一期的已实现特质波动率与收益的关系并不显著，只有在控制了非预期特质波动率时，预期特质波动率才与收益显著正相关。

以上关于特质波动率的研究主要讨论了股票特质波动率与截面收益率之间的相关性，整体来看国内外都没有形成统一的认识，原因在于研究结果与所用数据及估计特质波动率的方法有关。而另一些研究讨论了特质波动率因子的表现，Mc Lean发现特质波动率越高，反转效应越强，并且使用特质波动率作为权重能显著提升反转因子的效果，而动量效应与特质波动率并不相关。焦健采用规模分层提高了特质波动率因子的单调性，使得特质波动率从一个只有头尾区分性的因子升级为具有整体单调性的优质因子。柴宗泽同样考察了基于特质波动率的动量效应和反转效应，发现观察期或者持有期较长时，低特质波动率组合存在动量效应，高特质波动率组合存在反转效应。冯佳睿、袁林青发现特质波动率因子的选股效果自发现以来并没有减弱。

总的来看，关于特质波动率的研究多集中于特质波动率与截面收益率的关系上，而对特质波动率因子的研究较少。基于此，本文使用不同的方法、不同频率和时间范围的数据估计特质波动率，并从投资组合的策略表现角度，着重考虑不同估计的区别，以加深对特质波动率的理解，同时得到对投资者有参考意义的指导。

1 研究方法及数据说明

1．1 预期特质波动率的估计方法

本文采用三类不同的方法对特质波动率进行估计。

1．Fama-French三因子模型残差的标准差

参照Ang等，将Fama-French三因子模型的残差波动率，作为对特质波动率的估计IV1（也叫实现特质波动率）。具体地，在每个月末，对每只股票使用包括当月的最近k个月内（考虑k取1／3／6的情况）所有有交易的日度数据进行如下回归：

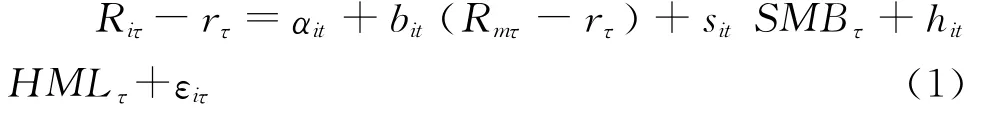
式中：i表示股票；τ表示交易日；t表示月份，τ∈t；Riτ为股票i在t月第τ日的收益率；rτ为t月第τ日的无风险收益率；Rmτ、SMBτ和HMLτ分别表示市场组合的收益率、市值因子收益率（小市值组合与大市值组合收益率之差）、账面市值比因子收益率（高账面市值比组合与低账面市值比组合的收益率之差）；bit、sit和hit分别是股票超额收益率对市场组合超额收益率、市值因子收益率以及账面市值比因子收益率的敏感系数；αit是股票i在t月的回归的常数项，εiτ是股票i在t月第τ日的回归残差项。

则股票i在t月的特质波动率为

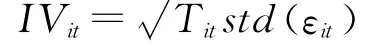
其中Tit为股票i在t月的交易天数；std（εit）为股票i在t月的残差项序列的标准差。

2．GARCH族模型

Fu等认为，用滞后一期的实现特质波动率估计预期特质波动率，暗含特质波动率是鞅过程，对其进行单位根检验发现当期的特质波动率不能较好地估计下期的值，因此他们使用EGARCH（p，q）模型估计特质波动率。基于此，本文将Fama-French三因子模型作为均值方程，对日度数据或月度数据使用GARCH（1，1）和EGARCH（1，1）模型估计特质波动率。

（1）GARCH模型：若使用日度数据，对每只股票，在t月末，使用包括该月交易数据的最近k月的日度数据，估计以下GARCH（1，1）方程的系数：

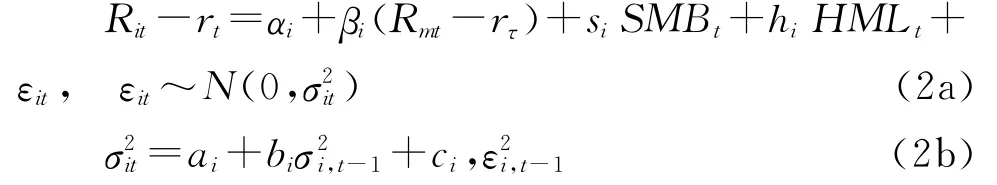
根据模型参数的估计值，将估计的σ2it序列的平均值作为对特质波动率的估计值IV2。

若使用的是最近若干月的月度数据，则将当月的波动率估计值σ2it作为对特质波动率的估计值IV2。

（2）EGARCH模型：对日度数据或月度数据，使用同上的方法估计以下EGARCH（1，1）模型，并得到估计值IV3。

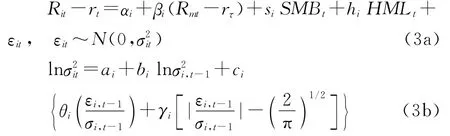
3．ARIMA模型

参考左浩苗等，本文首先估计每只股票每个月的三因素模型，得到各股票的月实现特质波动率的时间序列。t月末，使用包括t月的最近36个月的数据，对该序列采用拟合最优的ARIMA（p，q）过程（1≤p≤2，1≤q≤2，以最小AIC为标准选择最优模型），进行一步向前预测，得到特质波动率的估计值IV4。

1．2 其他变量的选取

为对比特质波动率因子与其他因子的选股效果，本文选取以下几个因素进行研究。

1．规模（mv）和账面市值比（BM）。规模与账面市值比分别代表了公司的市场特征和基本面特征。已有的研究表明，A股市场具有显著的市值效应和账面市值比效应。本文采用的规模变量定义为每个月月末、以亿为单位的股票总市值的对数，账面市值比定义为每个月月末、股票最新的账面价值与总市值的比值。

2．前一个月的收益率（R-1）。Jegadeesh和Titman发现美国市场存在显著的中期动量效应。国内股市动量效应的研究结果有所不同，朱战宇等、周琳杰、马超群和张浩均发现在中国市场只有形成期和持有期在4周内的周度策略中存在异常的动量收益。由此，本文以每只股票上个月末到当月月末的持有收益率衡量反转效应。

3．换手率（turnover）。杨华蔚等、左浩苗等发现换手率可以部分解释特质波动率与截面收益的负相关关系，而国内的研究表明换手率可以度量投资者异质性信念波动的程度（张峥和刘力），因此，本文以月换手率度量异质信念。

1．3 组合构建方法

以月为周期滚动调仓，每个月月末，在上市已满1年的全部沪深A股中，剔除ST股票、处于停牌状态的股票，以及当月实际交易天数不足当月总交易日的90%的股票，对剩余的股票使用当月的交易数据计算特质波动率（或其他变量）。根据计算结果将股票从低到高排序，并等分为5个投资组合，在下月第一个交易日按收盘价买入，并在最后一个交易日卖出，对买入当日涨停或停牌的股票放弃买入，卖出当日跌停或停牌的股票，延后至第一个有交易且收盘非跌停的交易日卖出，手续费按双边千分之三计，以等权的方式计算组合的收益率。多空组合的收益率用最低组的收益率减最高组的收益率得到。

1．4 样本数据

本文构建组合的时间段范围是2005年2月至2016年12月，共计143个交易月。由于某些模型估计参数需要较长时段的数据，本文所用的数据范围包括2000年初至2016年底沪深交易所交易的所有A股的日数据和月数据，包括所有股票的上市日期，每日的后复权收盘价、交易状态、是否ST、是否涨跌停，月末的总市值、账面价值，每月的换手率等，以上数据来自万德数据库。另外，用于三因素模型回归的Fama-French三因素日数据和月数据来源于国泰安数据库，所用的三因素数据使用流通市值加权来构建，无风险收益率采用央行公布的三月定存基准利率折算得到。

2 实证结果

2．1 不同方法估计特质波动率所构建组合的对比

首先考虑用日度数据估计特质波动率的方法。表1给出了用不同时长的日度数据，按照不同方法估计得到的特质波动率的统计特征，IV1使用Fama-French三因子回归残差的标准差估计，IV2使用GARCH（1，1）模型估计，IV3使用 GARCH（1，1）模型估计，由于对GARCH族模型的估计存在不收敛的情况，IV2和IV3的样本数都明显少于IV1。另外，无论使用哪种方法，对特质波动率的估计值都随着估计时间的增加而逐渐增大。

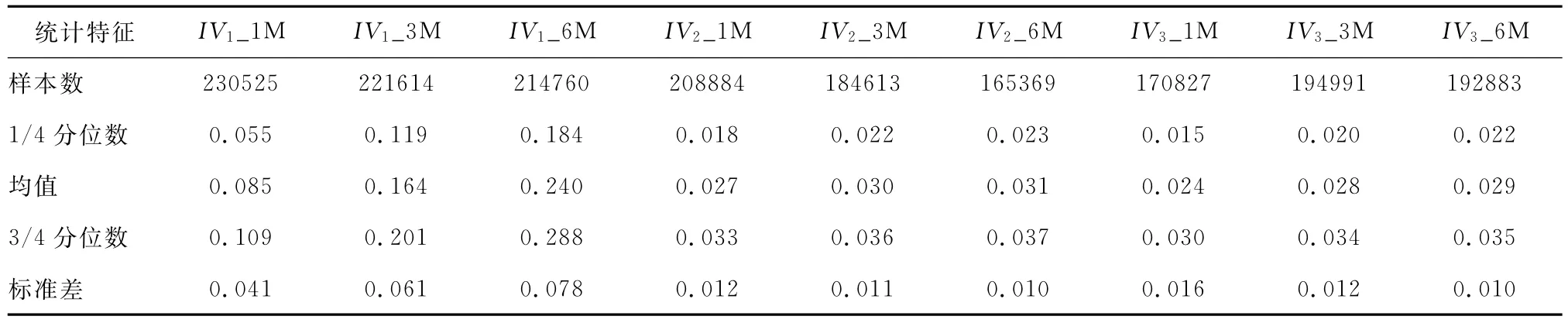
表1 使用日度数据，不同估计方法、不同估计时间得到的特质波动率的统计特征

表2给出了使用日度数据，基于不同估计特质波动率的多空策略组合的表现，包括组合月收益率的统计特征，组合的年化收益率、夏普比率、最大回撤，以及三因子回归的截距项。在三种不同的估计方法中，对于相同的估计时间，使用Fama-French三因子回归残差标准差得到的组合，每期交易的股票数量最多，表现也更好：其月均收益率更高，标准差更小，正偏程度以及超额峰度都更大，年化收益率和夏普比率明显更高，最大回撤也更小。其中，使用一个月数据估计的特质波动率组合表现最好，年化收益率高达22．06%，夏普比率达到了1．702，最大回撤仅为10．34%。另外，表2还显示，对于同一种方法，使用的估计时间越长，得到的多空组合的表现一般越差，说明时间越远的市场信息对投资者的指导意义越弱。

为检验不同估计方法对组合表现的差异是否由所交易股票样本的不同而引起，考虑对同样的估计时段，某只股票只有存在所有方法的估计值时，才将其列入待交易的股票池中，这一做法保证了股票样本一致，得到的结果与表2基本一致，限于篇幅此处不再列出。

对于使用月度数据的模型，参考Fu，本文考虑使用最近60个月的月度数据估计EGARCH（1，1）、GARCH（1，1）模型，以及基于最近36个月的实现特质波动率的 ARIMA（p，q）模型（1≤p≤2，1≤q≤2）。表3给出了使用月度数据，基于不同估计特质波动率的多空策略组合的表现。可以看到，根据GARCH（1，1）和 EGARCH（1，1）模型估计的特质波动率得到的组合，除EGARCH（1，1）表现与使用日度数据估计的组合相近外，月收益率均值、年化收益率、夏普比率甚至稍小于使用日数据估计的组合，不同之处在于使用EGARCH（1，1）模型的组合的最大回撤显著更低，不到9%。另外，使用ARIMA模型得到的组合表现介于GARCH族模型和实现波动率之间，这可能是因为部分实现波动率序列具有平稳性（邓春雪、郑振龙）。

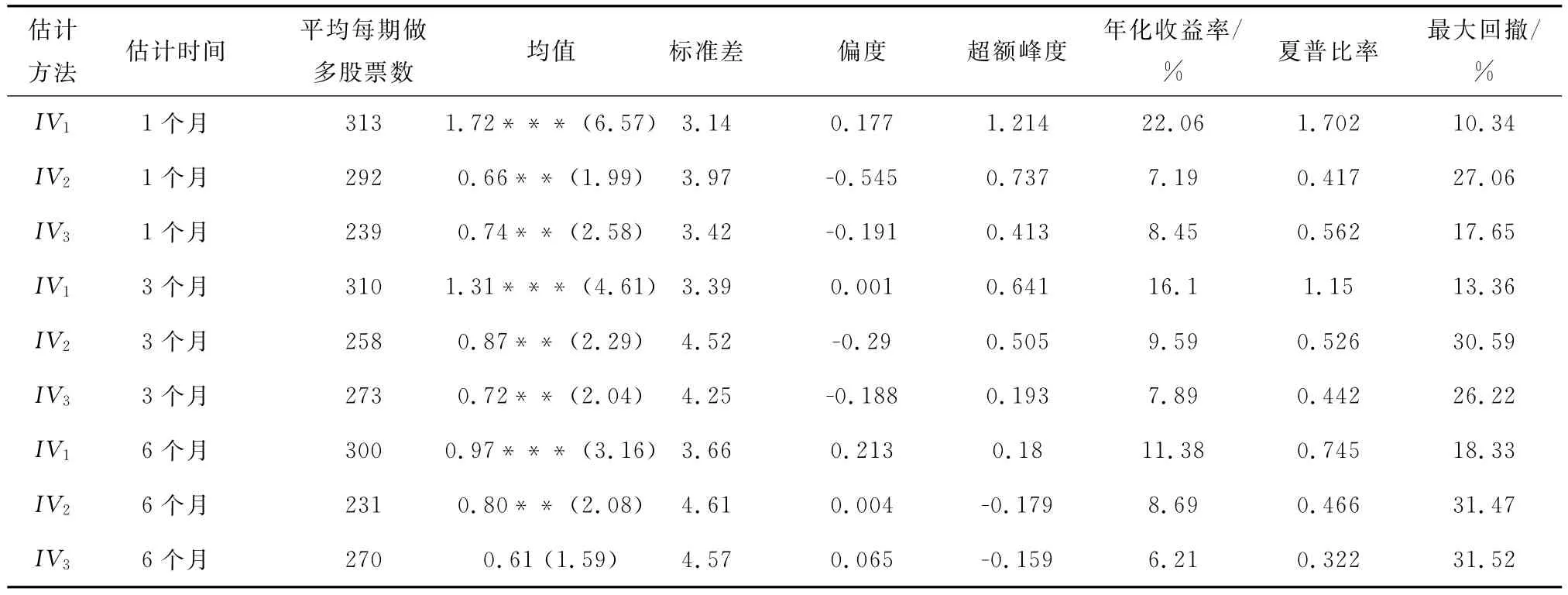
表2 使用日度数据，基于不同估计特质波动率的等权多空组合的策略表现

表4将基于实现特质波动率的多空组合，与市场组合以及基于其他分组变量形成的多空组合的表现进行对比。由该表，虽然实现特质波动率多空组合的月均收益率和年化收益率稍低于反转组合，但它有最大的夏普比率和最小的最大回撤，整体表现最好，而市场组合的夏普比率最低。

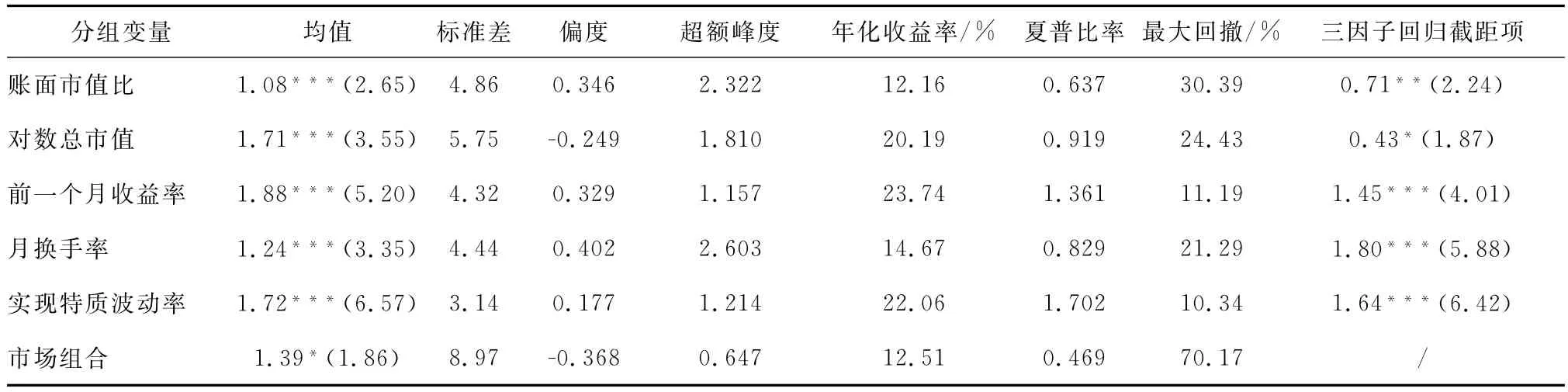
表4 单因子分组多空组合月收益率统计特征对比

2．2 根据实现特质波动率分组的各投资组合特征

以上结果表明，使用1个月的日数据估计实现特质波动率，并基于此形成的投资组合表现优于使用基于其他方法或数据估计的特质波动率的组合，也比使用其他变量形成的投资组合更好，以下考虑根据实现特质波动率分组的各投资组合特征。

表5统计了基于实现特质波动率的分组交易情况。在143个月中，每组交易的股票数量最少为163个，最多为517个，平均每月交易股票数量343个。另外，实现特质波动率越高，由于涨停或停牌无法买入，以及由于跌停或停牌卖出的情况越多。

表6统计了根据实现特质波动率分组的各组合表现。尽管各组合的夏普比率都不是很高，并且最大回撤都在50%以上，但是各组合的表现随特质波动率的增加呈现出单调变化，均值、偏度、超额峰度、年化收益率、夏普比率都随实现特质波动率严格递减，而标准差和最大回撤随之严格递增，这说明实现特质波动率是一个好的分组变量。

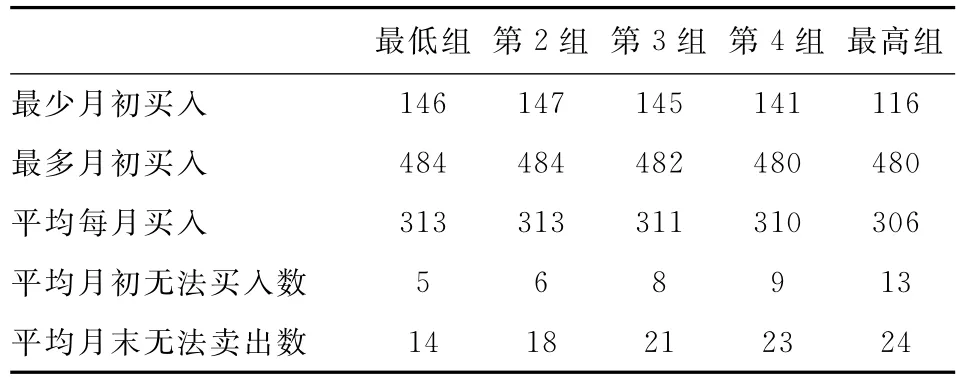
表5 根据实现特质波动率分5组，等权持仓、各组合交易股票情况

表6 根据实现特质波动率分5组，等权持仓，各组的月收益率统计特征等

表7给出了各分组组合的其他变量的平均值，由该表，实现特质波动率越高，账面市值比、对数总市值越小，而前一月收益率和月换手率则越高，这与表8显示的实现特质波动率多空组合的收益率与市值组合收益率负相关，与其他组合正相关一致。

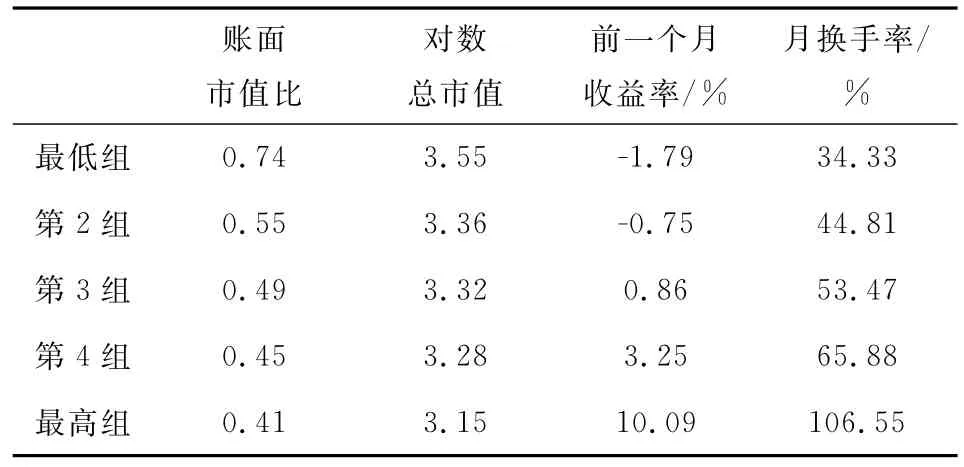
表7 根据实现特质波动率分5组，各组其他变量的平均值

表8 特质波动率多空组合与其他因子多空组合收益率相关系数

2．3 实现特质波动率多空组合的收益分解及改进

考虑实现特质波动率多空组合的收益来源，对多空组合月收益率进行多因子回归，表9给出了多元回归分析的结果，其中R＿M、SMB、HML分别为市场因子、市值因子、账面市值比因子，MOM、TUR分别表示参照Fama、French构建的动量因子和换手率因子。由该表，三因子模型下，截距项显著为正，组合市场收益率显著负相关，与市值因子的关系不显著，与账面市值比显著正相关且系数较大。单独加入动量因子或者换手率因子会降低截距及市场因子的绝对值和显著性，提高账面市值比的显著性并大幅增加调整后的R2，加入换手率因子后，市场因子的影响不再显著，而市值因子的影响则变为正显著，模型的解释力大幅提高。包含所有因子的模型中，系数及显著性从大到小依次为换手率、账面市值比、反转、截距项，市场因子则不再显著。这些结果与左浩苗等所发现的，在控制换手率之后，特质波动率与截面预期收益率之间的关系不再显著一致，说明特质波动率在一定程度上可以表征异质信念。

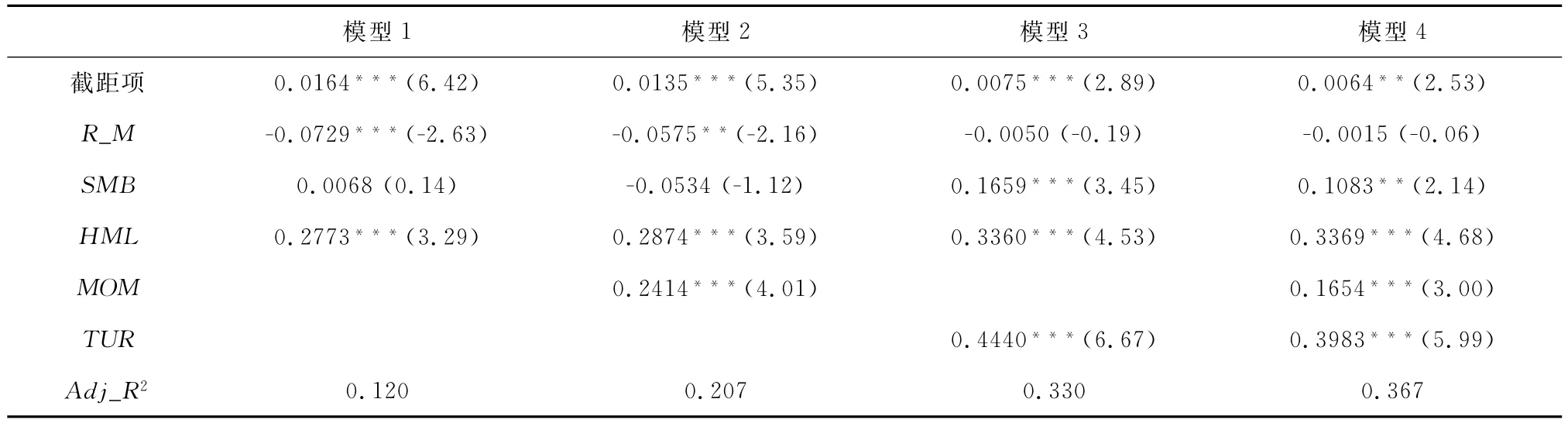
表9 实现特质波动率多空组合月收益率的回归分析

表9的模型1说明实现特质波动率多空组合的收益率与市场因子显著负相关，由此，实际中可以考虑利用市场组合进行对冲。简单起见，每个月末使用未对冲的组合最近12个月内的日数据，估计组合的β系数，对冲组合的收益率用原始组合收益率减去β与市场收益率之积。由于需要12个月的时间估计，对冲组合共有131个交易月。由表10，相比未对冲的组合，对冲组合的月均、年化收益率以及夏普比率都有所提高，最大回撤、收益率标准差、超额峰度等相差不大。图1也直观地反映了对冲组合的表现确实稳定地优于未对冲组合。

表10 对冲与未对冲的多空组合对比

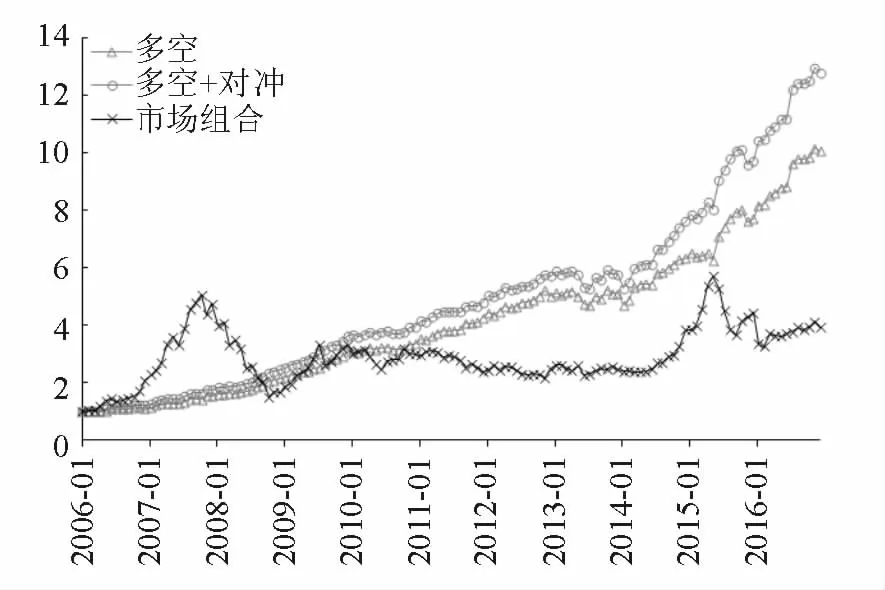
图1 对冲、未对冲组合与市场组合的对比

3 小结

本文首先使用三因子模型回归残差波动率、EGARCH（1，1）、GARCH（1，1）以及 ARIMA 等不同估计方法，基于不同频率或时段的数据估计特质波动率，进一步构造多空组合，对比发现使用Ang等提出的三因子残差波动率（实现特质波动率），基于1个月的日度数据估计的特质波动率，得到的投资组合的表现显著优于其他方法得到的组合，而GARCH族模型估计的特质波动率构造的多空组合表现一般，但是其年化收益率多数为正，这支持了左浩苗等的结论，并与田益祥、刘鹏等人的结果相反。同时，该组合也优于使用账面市值比、市值、前1个月收益率、换手率等指标分组构建的多空组合。

对基于实现特质波动率的组合分组统计，发现特质波动率越高，账面市值比、市值越小，前期收益率及换手率越高，组合收益率与市值因子负相关，与其他因子正相关。进一步对月回归进行分析，可知换手率因子对组合收益率的解释力最大，这与国内已有的研究一致，说明特质波动率因子的收益率可以由异质信念解释。