高斯辅助粒子算法

宋昊霖

摘 要：粒子滤波算法在处理非线性，非高斯问题的状态估计方面有独特的优势。粒子滤波方法由于存在粒子退化，粒子多样性匮乏等问题，不能准确地估计系统状态。该文提出了一种新的粒子滤波算法-高斯辅助粒子滤波算法，将即时的观测值信息引入重要性概率密度函數当中。该研究进行重采样时，用高斯变换对粒子进行了重新分布并调整重采样后的粒子权值。通过仿真实验验证该方法可以有效运用当前观测量值，优化粒子分布，在解决粒子退化问题的同时，也能维持粒子的多样性，提高滤波效率。

关键词：粒子滤波 重要性密度函数 重采样 高斯辅助粒子滤波

中图分类号：TP24 文献标识码：A 文章编号：1672-3791（2019）01（a）-00-03

Abstract：Particle filter algorithm has a unique advantage in dealing with nonlinear， non-Gaussian state estimation. Particle filter method cannot accurately estimate the state of the system due to the particle degeneration and lack of particle diversity. In this paper， we propose a new particle filter algorithm called “Gauss based auxiliary particle filter” that introduces the real-time observation information into the importance probability density function. During resampling step， the particles are redistributed using Gaussian transformation and the weights of the particles after resampling are adjusted. The simulation results illustrate that the proposed method can effectively use the current values and optimize the particle distribution. This algorithm cannot only solve the problem of particle degeneration， but it can also maintain the diversity of particles and improve the filter efficiency.

Key words：particle filter； mportance probability density function； resample； gauss based Auxiliary particle filter

随着信息技术的不断发展，非线性系统状态估计已逐渐成为一个受到国内外学者重视的热点研究课题。随着实际应用对模型的复杂性和滤波精度要求不断提高，卡尔曼滤波等传统的滤波方法已远远不能满足实际使用要求[1]。粒子滤波技术作为一种非线性数值滤波方法，可以高效地处理非线性、非高斯动态系统状态估计[2]。在面向更复杂的非线性模型时，无需对非线性系统做线性估计，更符合实际滤波的要求[3]。

为了改善粒子滤波算法存在的多样性匮乏问题，提高粒子滤波算法的收敛性，提高算法运行速度，改善粒子退化问题，扩展算法的新的应用领域[4]，该文提出了一种改进的粒子滤波算法，即高斯辅助粒子滤波算法，此算法是在辅助粒子滤波算法的基础上，对重采样粒子的状态进行高斯变换使粒子重新分布，并对变换后的粒子权值进行调节，以改进常规重采样算法造成的多样性缺失问题。

1 高斯辅助粒子滤波算法

根据粒子滤波算法的要求，在预测下一时刻的粒子集时，不但要参考已有的粒子还要考虑最新的观测粒子。理想的状态是将即时的观测值信息引入重要性概率密度函数当中，如此不但可以提高滤波效率，也可以充分地运用当前的观测量框架。为此，提出了辅助粒子滤波，引入了一个辅助变量，充分利用系统当前时刻的观测值，对k时刻的状态转移演化粒子状态进行相应调整，使系统分布更合理、更贴近真实状况。

但从辅助粒子滤波的原理可知，当粒子权值变异较大时就需要进行重采样，但过多的重采样又会导致粒子缺乏多样性，最终整个粒子集中具有过多的重复粒子，粒子集已不能准确地估计系统的状态。因此，需要对辅助粒子滤波的重采样步骤进行改进，改变常规重采样方法对小权值粒子直接舍弃，对大权值粒子进行复制的特点，用高斯变换生成重采样粒子，对粒子进行了重新分布并调整重采样后的粒子权值，在解决粒子退化问题的同时，也能维持粒子的多样性。

3 算法比较

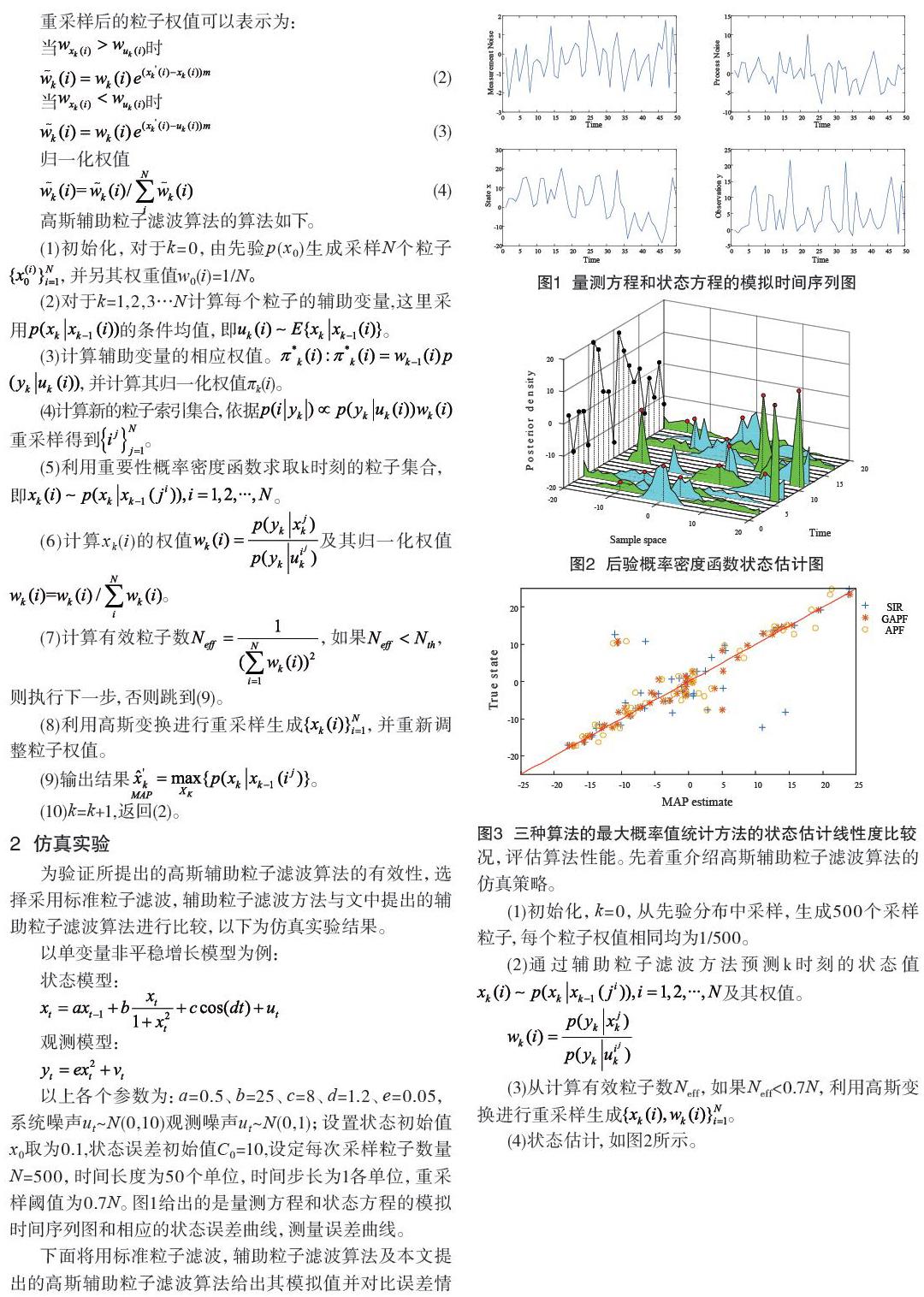
图3为标准粒子滤波算法（“+”），辅助粒子滤波（“o”），高斯辅助粒子滤波曲线（“*”）估计出的模拟量的对比图，图3显示的是状态估计期望值的线性度以及最大估计权值的粒子线性度。通过3种方法对比可以看出，标准粒子滤波方法效果最差，离真值的差异最大，高斯辅助粒子滤波算法比常规的辅助粒子滤波算法有所改进，估计值距离真值的差异也在减小。

由图3中数据可知，标准粒子滤波算法的误差最大，高斯辅助粒子滤波算法优于常规辅助粒子算法，说明改进的辅助粒子算法的跟踪性能最好，最接近系统真值。

4 结语

粒子滤波算法由于重要性概率密度函数和重采样方法选取的不理想，导致样本与真实后验分布抽样存在较大偏差，粒子多样性匮乏，系统的估计精度降低。本文提出的高斯辅助粒子滤波算法，将当前时刻的观测值信息引入重要性概率密度函数中，充分运用当前的观测值，达到提高滤波效率的目的。在进行粒子重采样时，通过高斯变换对粒子进行重新分布并调整粒子权值，提高样本的多样性与准确性。最后通过仿真实验，从算法的线性度方面比较了标准粒子滤波算法，辅助粒子滤波算法和高斯辅助粒子滤波算法。仿真结果表明，高斯辅助粒子滤波算法总体上性能明显优于标准粒子滤波算法和辅助粒子滤波算法，高斯辅助粒子滤波算法避免了采样粒子的退化和匮乏，有效提高了粒子滤波算法的效率与精度，能够在实际应用中提高估计精度。

参考文献

[1] AlanE.Gelfand，AdrianF.M.Smith.Sampling-Based Approaches to Calculating Marginal Densities[J]. Journal of the American Statistical Associati-on，2015，85（410）：398-409.

[2] 胡士强.粒子滤波原理及其应用[M].北京：科学出版社，2010.

[3] Sun J，Wu X，Palade V，et al.Random drift particle swarm optimization algorithm： convergence analysis and parameter selection[J].Machine Learning，2015，101（1-3）：345-376.

[4] Wu J，Song S，An W，et al.Defect Detection and Localization of Nonlinear System Based on Particle Filter with an Adaptive Parametric Model[J].Mathematical Problems in Engineering，2015（6）：1-12.