基于渐进均匀化方法的土工格室材料设计与应用

印长俊，舒亮，潘婷，李卓，肖鹏



基于渐进均匀化方法的土工格室材料设计与应用

印长俊1, 3，舒亮2，潘婷1，李卓4，肖鹏1

(1. 湘潭大学 土木工程与力学学院，湖南 湘潭 411105； 2. 湖南省怀化公路桥梁建设总公司，湖南 怀化 418000； 3. 岩土力学与工程安全湖南省重点实验室，湖南 湘潭 411105； 4. 湘潭大学 机械工程学院，湖南 湘潭 411105)

土工格室加筋层设计应考虑其各向异性的力学性能，利用试验方法测得所有各向异性常数较为困难。通过对土工格室加筋层代表体积单元进行多尺度分析和加筋路堤实体建模仿真，得到所需参数。计算结果表明：采用渐进均匀化方法能够计算三维土工格室加筋层的等效弹性常数，并推导出杨氏模量、泊松比和剪切模量；土工格室的铺设方式对加筋层水平方向的杨氏模量、泊松比和剪切模量有显著影响；加筋层水平方向的泊松比分量为负值，表明加筋层在该平面内有负泊松比特性；土工格室在路基中采用45°铺设方式比采用0°铺设方式可减少路基水平方向的变形值，但对竖向沉降几乎没有影响。

土工格室；渐进均匀化方法；材料设计；多尺度；负泊松比

目前，国内外有关土工格室材料设计的研究已经取得了许多有意义的成果[1−3]。试验研究方面：Madhavi等[4]通过试验方法针对土工格室抗拉强度、格室高度和格室片材长度对路堤承载力以及路堤变形的影响进行了研究。顾良军等[5]通过室内静力承载板试验探究格室内填土对加筋层力学性能的影响，结论是格室内填土的压实度越大，强度越大。高昂等[6]通过改变加筋层数、格室高度和焊距探究路堤承载力的影响因素，静动载试验结果表明以上3种因素均对路堤承载力有不同程度的影响。孙州等[7]对土工格室加固路堤在条形荷载作用下路堤变形情况进行了模型试验研究，通过控制路堤边坡土体的压实度、土工格室铺设层数、埋设深度以及格室焊距等条件分析路堤的承载力、路堤边坡的侧向变形和破坏形式的规律。数值研究方面：Costa等[8]基于2.5维有限元−边界元模型研究了土工格室加筋层刚度及格室埋设深度对路堤力学性能的影响。ZHANG等[9]运用解耦迭代法分析得出格室内填土的非线性对加筋层力学性能的影响。目前的数值计算方法大多将二维格室模型简化为杆单元或复合体，三维格室模型简化为膜单元。上述模型不能模拟格室与填料间的相互作用，如嵌锁作用和摩擦作用[10]。针对该相互作用，Dash等[11−13]分别通过直剪试验、建立土工格室加筋层简化模型和现场试验方法进行了研究，研究结果均表明格室与填料间的相互作用至关重要，不可忽略。鉴于此，邓鹏 等[14]借助有限元分析软件Abaqus建立了土工格室仿实体模型，对填料−格室间的相互作用进行了模拟，分析了格室内填料的强度、格室刚度和路基的压缩性能对路堤力学性能的影响，并通过路堤模型试验验证了计算模型。上述研究只能单独从宏观或细观角度研究土工格室加筋层的性能，试验研究成本高且不具有普遍性。而多尺度方法具有从宏细观角度进行非均质材料设计的优势，并且数值模拟过程相对简单，成本较低。目前运用渐进均匀化方法(Asymptotic Homogenization Method, AHM)[15−16]分析土工格室加筋层力学性能的研究相对较少，本文针对土工格室的铺设方式，采用AHM从宏细观角度分析了土工格室材料参数对加筋层力学性能的影响。

1 渐进均匀化方法

AHM利用严格的数学方法以求解非均质材料的多尺度问题，至今已有30多年。该方法能够计算非均质材料的等效弹性常数和细观内力。

Hassani等[17]已对AHM的解析解法和数值解法做过详细论述，给出了求解2D问题的推导过程，本文将对3D问题进行简单推导。3D问题需要求解6种工况得到等效弹性矩阵[]的12个分量，其矩阵形式为：

弹性矩阵中C(,=1, 2, 3,…, 6)是弹性常数。对于正交各向异性材料弹性矩阵的逆矩阵[]−1可用杨氏模量E(=1, 2, 3)，泊松比υ(,=1, 2, 3)，剪切模量G(,=1, 2, 3)来表示：

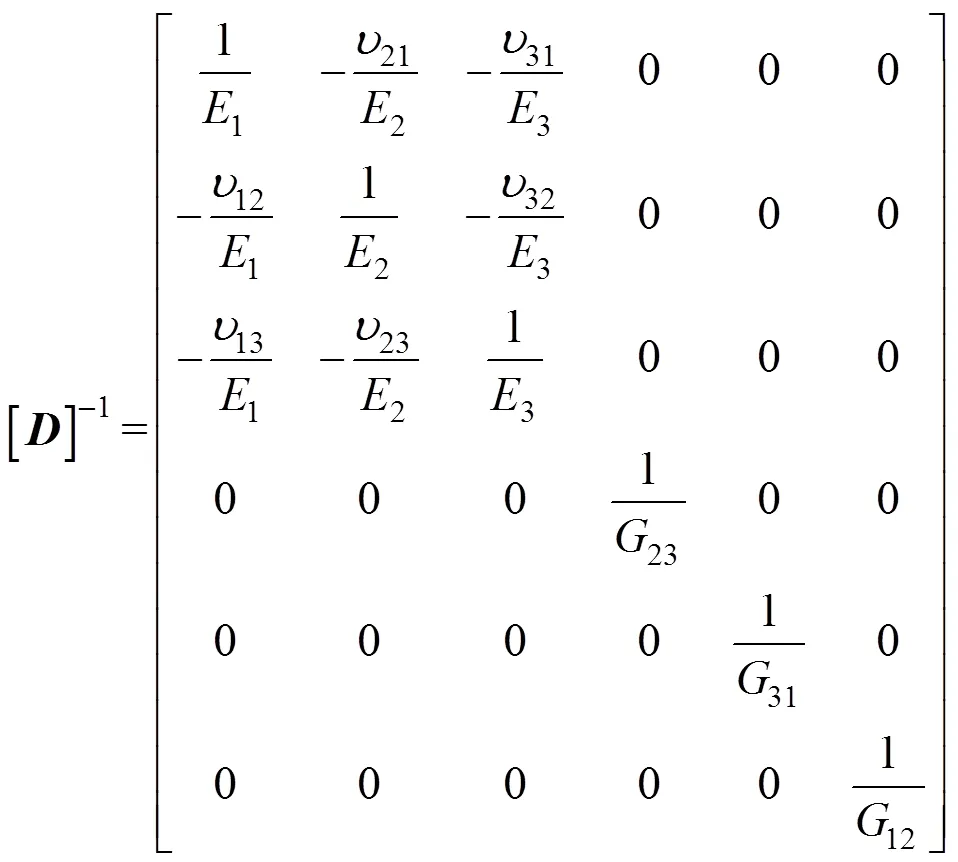
如图1所示，式中1，2和3分别是，和方向加筋层的杨氏模量；12和13为方向作用应力引起的方向和方向应变的泊松比，21和23为方向作用应力引起的方向和方向应变的泊松比，31和32为方向作用应力引起的方向和方向应变的泊松比；12，23和31分别是，和平面的剪切模量。

因为AHM只能计算出弹性矩阵[]，并不能直接求得加筋层杨氏模量，于是需将式(1)中的弹性矩阵[]求逆，求得的逆矩阵的每一项与式(2)中的对应项相等，建立12个方程并求解，得出杨氏模量E，泊松比υ和剪切模量G。

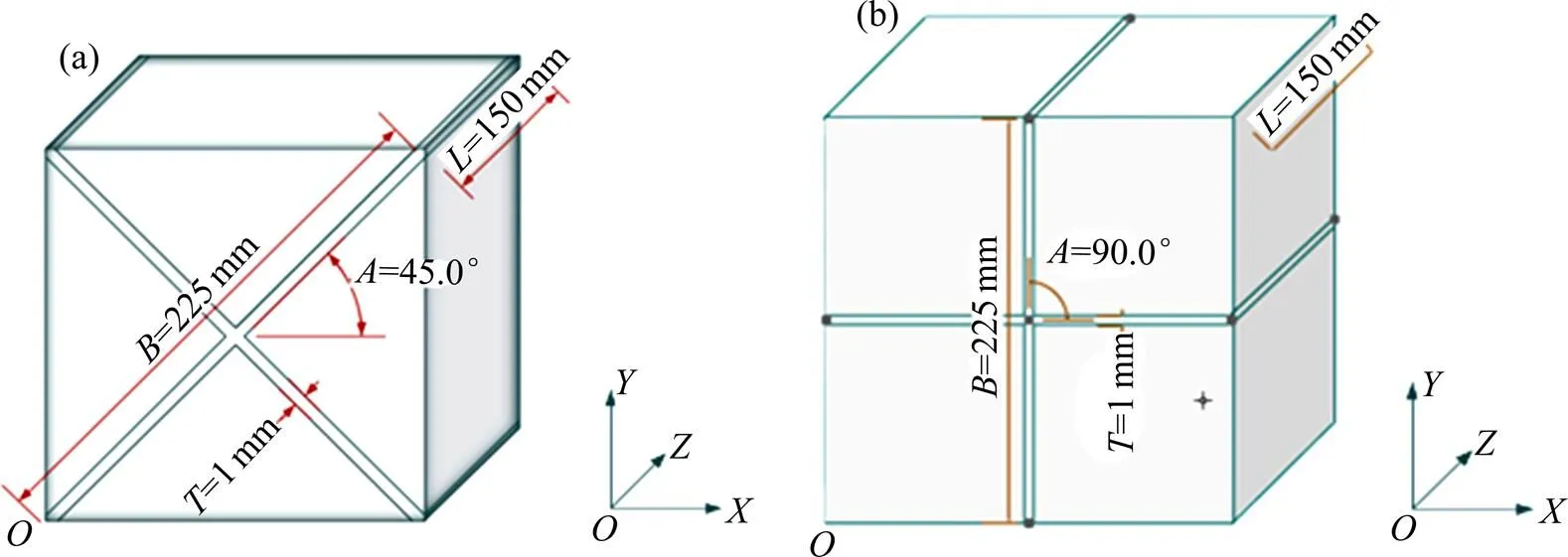
(a) 45°铺设；(b) 0°铺设

2 算例分析

考虑土工格室的铺设方式可能对其力学性能有较大影响，为此针对格室片材与路基纵向(图1中的方向)夹角为45°时的铺设方式和0°时的铺设方式分别建立土工格室加筋层代表体积单元(Representative Volume Element, RVE)(图1)。土工格室规格取自文献[18]中的Test 2：焊距=225 mm，厚度=1 mm，高度=150 mm，此时格室的体积率均为0.889 6%。其中45°铺设方式的格室RVE长度和宽度均为159.10 mm，厚度为150.00 mm。0°铺设方式的格室RVE长度和宽度均为225.00 mm，厚度为150.00 mm。

运用AHM求解土工格室加筋层的等效弹性常数，首先需确定土工格室和室内填料的力学参 数[18]，如表1；然后对RVE模型施加周期边界条件；最后求解各个工况下的等效弹性常数。

表1 土工格室及填料的力学参数

运行自己编制的AHMP程序[19−20]，分别求得土工格室45°铺设和0°铺设时的加筋层弹性矩阵。

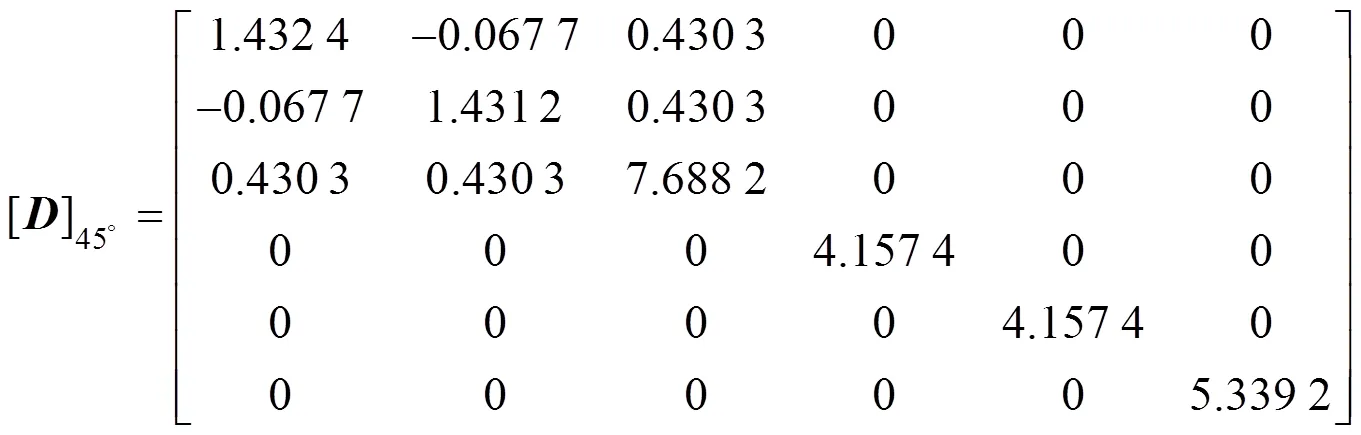
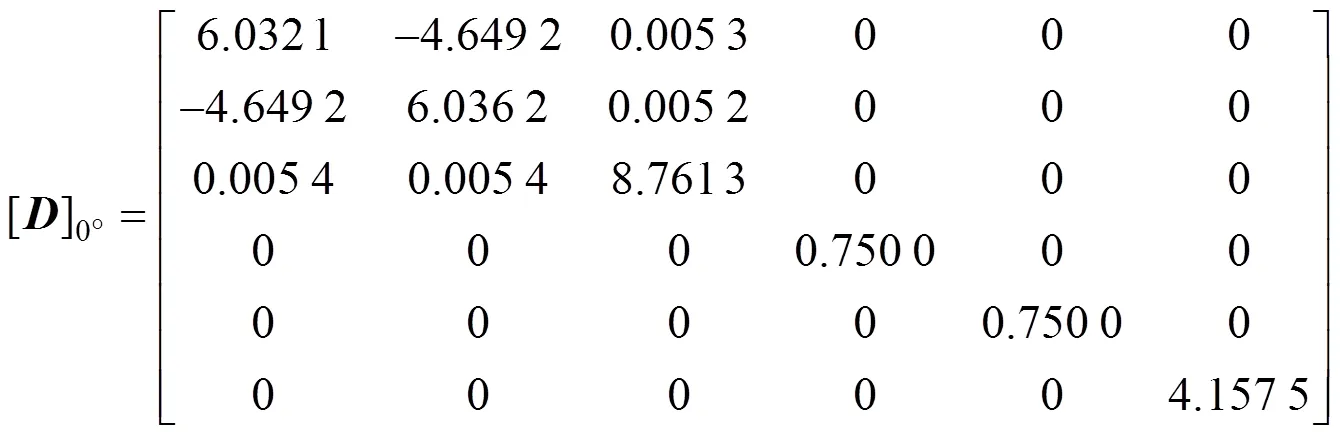
将弹性矩阵(3)和(4)分别求逆，并将所得结果与式(2)的对应项相等，分别建立方程组并求解。计算结果如表2所示。由表2可知：1) 45°铺设的土工格室加筋层竖向杨氏模量7.417 MPa小于0°铺设时的8.756 MPa，其变化率为18.05%，两者均接近参考试验的竖向杨氏模量试验值6.12 MPa[18]，表明AHM用来计算加筋层的杨氏模量是可靠的。2) 45°铺设时加筋层水平方向的杨氏模量1.402 MPa小于0°铺设时水平方向的杨氏模量2.450 MPa，其变化率为74.74%。3) 不同铺设方式下，方向的剪切模量分别为5.339 MPa和4.158 MPa，变化率为22.12%；而和方向上的剪切模量分别为4.157 MPa和 0.75 MPa，变化率达到了81.96%，即变化较大。同样，各方向的泊松比也有很大程度的变化。结果表明土工格室的铺设方式对加筋层杨氏模量、和方向剪切模量以及泊松比均有显著影响，而对于加筋层竖向杨氏模量和方向剪切模量均无显著影响。

由表2还可知，2种铺设方式的土工格室加筋层水平方向的泊松比12和21均为负值[21]。材料泊松比理论范围为[−1, 0.5]，当泊松比为负值，其特征表现为当材料受外力拉伸时垂直方向发生膨胀变形而在受压时垂直方向发生收缩变形。负泊松比特征对土工格室加筋层的工程应用是否有利还需进一步研究。

表2 不同铺设方式下土工格室加筋层的杨氏模量、泊松比和剪切模量

3 路基变形的计算

3.1 有限元模型的建立

为探究土工格室铺设方式对路基变形特征的影响，分别针对格室45°铺设方式和0°铺设方式建立参考试验路基模型[18]，模型尺寸如图2所示。

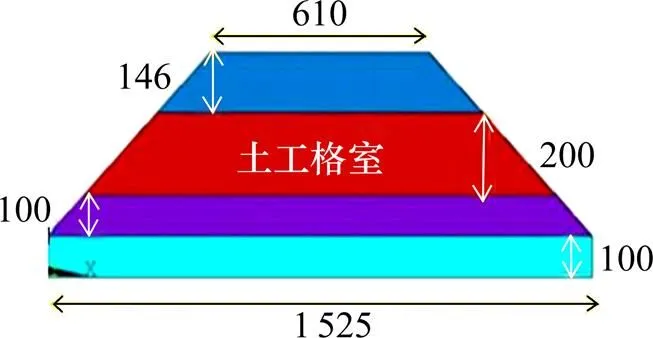
单位：mm

路基底部的水平宽度为1 525 mm，顶部的水平宽度为610 mm，整体的垂直高度为446 mm，垫层的厚度为100 mm。

数值模型结果有2个来源。其一是文献[18]中的数值模型结果，该模型中土工格室层包含2种材料，选用广义胡克定律作为土工格室的本构模型，而铁路道砟选用弹塑性模型中的D-P本构模型。建立模型时，铁路道砟的相关参数和加筋层材料参数均根据文献[18]中的大型三轴试验的实际工况选取。其二是在前述模型基础上，将图2中的土工格室加筋层等效为各向异性均匀化材料，利用AHM所得的2种铺设方式加筋层材料参数分别进行模拟。垫层参数则采用木质垫层通常所选用的规格。以上材料的具体参数如表3所示。

采用ANSYS软件对参考试验路基进行建模。施加与参考文献[18]中一系列大型三轴试验实际工况相同的边界条件：底部边界设置为全约束；垫层侧向边界条件为只约束法向变形。随后进行网格划分，分别将大小为175，225，275，325，350，375，400，425，450，475，500和525 kPa的竖向荷载作用在路基顶部中间部分152 mm×152 mm区域的所有节点上(图3)。

3.2 模拟结果与分析

对不同的材料参数来源的有限元模型分别进行数值模拟。将试验变形值、依据试验参数的计算变形值、依据均匀化参数的计算变形值分别进行对比，如图4所示。

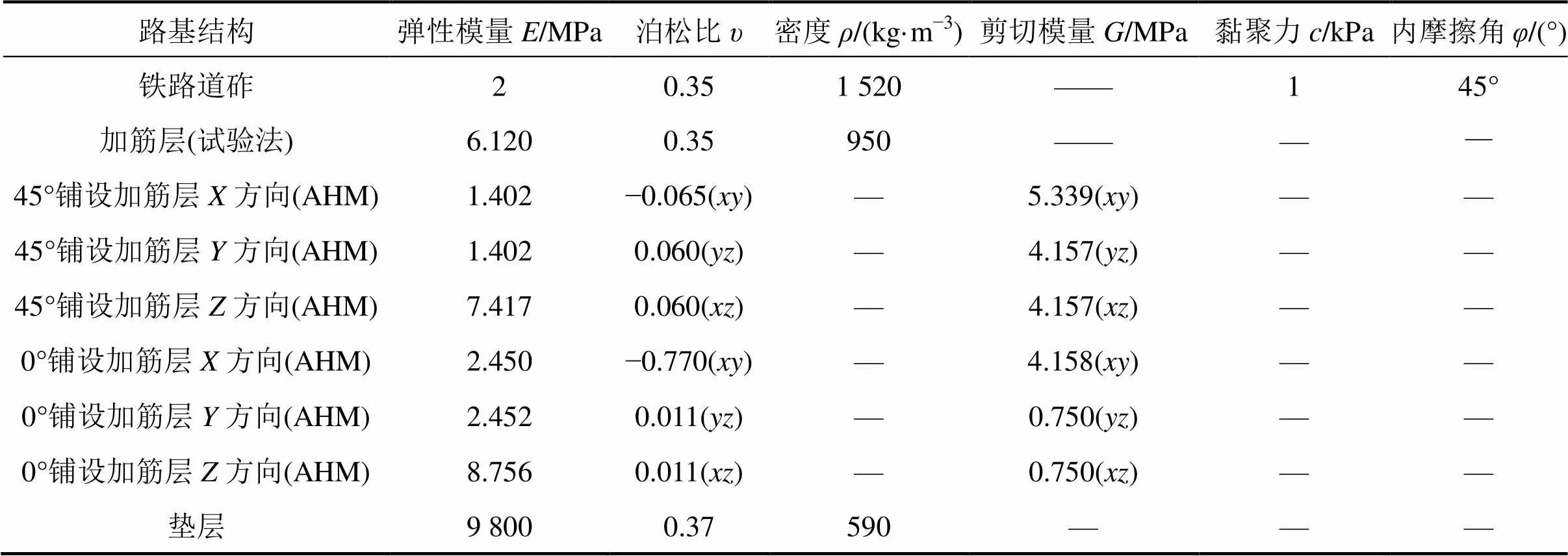
表3 模型计算参数

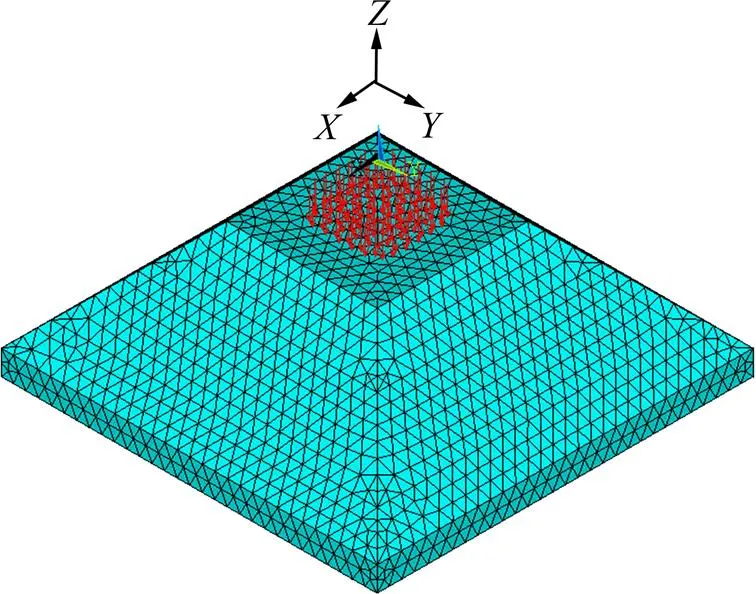
图3 路基有限元模型

由图4(a)可知，路基模型的沉降计算值与实验室试验值吻合较好。当施加175，225，275，300和325 kPa的荷载时，文献[18]的数值计算果与本文结果的沉降值相差约在1~3 mm之间，当荷载增加到350 kPa后两者的结果更为接近，约在0~1 mm之间。而整个数值计算结果均小于试验值，相差约在0~6 mm之间，其计算精度是在可接受范围内的。由此证明利用源于AHM计算的各向异性材料参数用于土工格室加筋层沉降的计算是合理有效的。

由图4(b)可知，路基模型的水平方向最大位移计算值与实验室试验值趋势基本一致，但是试验值的曲线斜率明显大于所有数值计算值曲线斜率，对于这一差异文献[18]的解释是：这是由于各向异性无黏性材料受低围压时的塑性变形很难被预测而造成的。如大部分类似颗粒的材料，其横向位移一般发生在土工格室顶点或者侧面处。尽管模型有不足之处，但其图线的变化趋势与试验值是一致的，并且路基所发生的水平方向位移与试验结果在相同的数量级内，因此模拟结果在可接受的范围之内。图4(b)中显示，路基水平方向产生的最大位移的数值计算结果按照从小到大的顺序依次是：格室45°铺设时的计算值＜文献[18]试验方法的计算值＜格室0°铺设时的计算值。

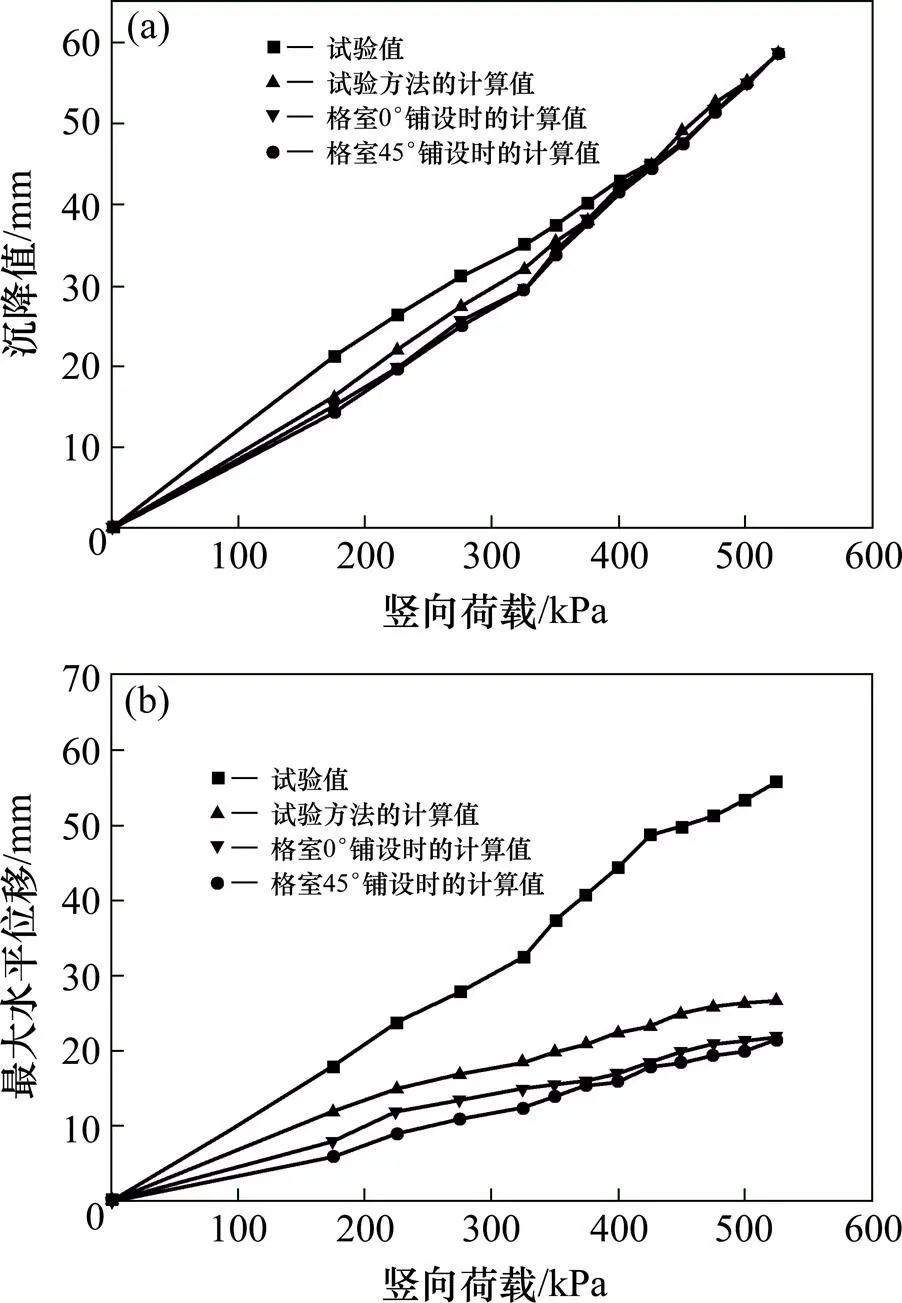
(a) 竖向荷载下路基沉降值；(b) 竖向荷载下路基水平方向最大位移

利用源于AHM计算所得参数的数值计算分析结果可知：

1) 表2中显示，土工格室45°铺设时，加筋层各平面的剪切模量均大于格室0°铺设时的剪切模量。剪切模量越大，材料的刚性越强，其抵抗切应变的能力越强。

2) 图4(a)中显示，当路基产生的沉降值大小相同时，土工格室45°铺设时的路基沉降值小于0°铺设时的路基沉降值。

3) 图4(b)中显示，当加筋路基承受竖向荷载时，45°铺设时路基水平方向最大位移明显小于0°铺设时的水平方向最大位移。

综合上述结果可得，从减少路基水平方向变形角度来说，在路基中采用45°铺设方式优于采用0°铺设方式。

4 结论

1) 源于AHM计算所得的土工格室三维结构各向异性等效弹性常数的用于计算土工格室加筋层的变形是可行的，这为研究非均质材料的宏观力学性能提供了一种参考方法。

2) 土工格室的铺设方式对土工格室加筋层的杨氏模量、剪切模量和泊松比有显著影响。该计算结果将对土工格室加筋层的材料设计与其在实际工程中的应用提供参考。

3) 45°铺设方式和0°铺设方式的土工格室加筋层都具有水平方向的负泊松比特性。

4) 土工格室在路基中采用45°铺设方式比采用0°铺设方式可减少路基水平方向的变形值。

[1] HAN J, YANG X M, Leshchinsky D, et al. Numerical analysis for mechanisms of a geocell-reinforced base under a vertical load[J]. Geosynthetics in Civil and Environmental Engineering, Springer, Berlin, Heidelberg, 2008: 741−746.

[2] Sireesh S, Sitharam T G, Dash S K. Bearing capacity of circular footing on geocell–sand mattress overlying clay bed with void[J]. Geotextiles and Geomembranes, 2009, 27(2): 89−98.

[3] 晏长根, 顾良军, 杨晓华, 等. 土工格室加筋黄土的三轴剪切性能[J]. 中国公路学报, 2017, 30(10): 17−24. YAN Changgen, GU Liangjun, YANG Xiaohua, et al. Triaxial shear properties of geocell-reinforced loess[J]. China Journal of Highway and Transport, 2017, 30(10): 17−24.

[4] Madhavi L G, Rajagopal K, Krishnaswamy N R. Experimental and theoretical investigations on geocell- supported embankments[J]. International Journal of Geomechanics, 2006, 6(1): 30−35.

[5] 顾良军, 谢永利, 杨晓华. 土工格室结构层工程性状试验研究[D].西安: 长安大学, 2004. GU Liangjun, XIE Yongli, YANG Xiaohua. Experimental study on engineering properties of geocell structural layer[D]. Xi’an: Chang’an University, 2004.

[6] 高昂, 张孟喜, 朱华超, 等. 循环荷载及静载下土工格室加筋路堤模型试验研究[J]. 岩土力学, 2016, 37(7): 1921−1928, 1946. GAO Ang, ZHANG Mengxi, ZHU Huachao, et al. Experimental study on geocell-reinforced embankment model under cyclic loading and static load[J]. Rock and Soil Mechanics, 2016, 37(7): 1921−1928, 1946.

[7] 孙州, 张孟喜, 姜圣卫. 条形荷载下土工格室加筋砂土路堤模型试验研究[J]. 岩土工程学报, 2015, 37(增2): 170−175. SUN Zhou, ZHANG Mengxi, JIANG Shengwei. Experimental study on embankment model of geomer reinforced sandy soil under strip load[J]. Journal of Geotechnical Engineering, 2015, 37(Suppl 2): 170−175.

[8] Costa P A, Calçada R, Cardoso A S. Ballast mats for the reduction of railway traffic vibrations. Numerical study[J]. Soil Dynamics and Earthquake Engineering, 2012, 42(4): 137−150.

[9] ZHANG L, ZHAO M, SHI C, et al. Nonlinear analysis of a geocell mattress on an elastic–plastic foundation[J]. Computers and Geotechnics, 2012, 42(3): 204−211.

[10] YANG X. Numerical analyses of geocell-reinforced granular soils under static and repeated loads[D]. Kansas: University of Kansas, 2010.

[11] Dash S K, Shivadas A S. Performance improvement of railway ballast using geocells[J]. Indian Geotechnical Journal, 2012, 42(3): 186−193.

[12] 边学成, 宋广, 陈云敏. Pasternak地基中土工格室加筋体的受力变形分析[J]. 工程力学, 2012, 29(5): 147−155. BIAN Xuecheng, SONG Guang, CHEN Yunmin. Deformation behaviors of geocell-reinforcement in Pasternak ground[J]. Engineering Mechanics, 2012, 29(5): 147−155.

[13] Indraratna B, Nimbalkar S, Christie D, et al. Field assessment of the performance of a ballasted rail track with and without geosynthetics[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(7): 907−917.

[14] 邓鹏, 郭林, 蔡袁强, 等. 考虑填料−土工格室相互作用的加筋路堤力学响应研究[J]. 岩石力学与工程学报, 2015, 34(3): 621−630. DENG Peng, GUO Lin, CAI Yuanqiang, et al. Study on the mechanical response of reinforced embankment considering the interaction of filling and geocell[J]. Journal of Rock Mechanics and Engineering, 2015, 34(3): 621−630.

[15] Bensoussan A, Lions J L, Papanicolaou G. Asymptotic analysis for periodic structures[M]. New York, America: AMS Chelsea Publishing, 2011.

[16] Sanchez-Palencia E. Non-homogenous media and vibration theory[M]. Berlin, Heideberg, New York: Springer-Verlag, 1980.

[17] Hassani B, Hinton E. A review of homogenization and topology optimization II—analytical and numerical solution of homogenization equations[J]. Computers & Structures, 1998, 69(6): 719−738.

[18] Leshchinsky B, Ling H. Effects of geocell confinement on strength and deformation behavior of gravel[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 139(2): 340−352.

[19] 印长俊. 周期性复合材料等效模量计算软件: 中国, 2012SR113371[P]. 2012. YIN Changjun. Periodic composite equivalent modulus calculation software: China, 2012SR113371[P]. 2012.

[20] 印长俊, 肖鹏, 屈畅姿. 用渐进均匀化方法分析混凝土的弹性常数[C]// 中国力学大会. 北京, 2017. YIN Changjun, XIAO Peng, QU Changzi. Computing elastic constants of concrete based on asymptotic homogenization method[C]// CCTAM 2017. Beijing, 2017.

[21] Lakes R, Wojciechowski K W. Negative compressibility, negative Poisson's ratio, and stability[J]. Physica Status Solidi, 2008, 245(3): 545−551.

Design and application of geocell material based on asymptotic homogenization method

YIN Changjun1, 3, SHU Liang2, PAN Ting1, LI Zhuo4, XIAO Peng1

(1. School of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China; 2. Hunan Huaihua Highway and Bridge Construction Corporation, Huaihua 41800, China; 3. Rock and Soil Mechanics and Engineering Safety Key Laboratory of Hunan Province, Xiangtan 411105, China; 4. School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

Anisotropy mechanical properties should be concerned as designing the geocell-reinforcement of embankment, and measuring all anisotropic constants is difficult by experimental method. The required parameters were obtained by the multi-scale analysis of representative volume elements (RVE) of the geocell-reinforcement and simulation of the reinforced embankment. The conclusions are summarized as follows: The equivalent elastic constants of the 3D geocell-reinforcement could be computed by AHM, and Young’s modulus, Poisson’s ratio and shear modulus are deduced by using these; Laying method of geocell affected markedly the mechanical parameters such as Young’s modulus, Poisson’s ratio and shear modulus of the geocell-reinforcement; The Poisson’s ratio components in horizontal direction of the geocell-reinforcement are negative, which indicates that the geocell- reinforcement has a negative Poisson’s ratio characteristic in horizontal direction; Comparing with adopting the 0° laying method of geocell, adopting the 45° laying method of geocell could reduce horizontal deformation values of embankment, but has little effect on the vertical settlement of embankment.

geocell; asymptotic homogenization method; material design; multi-scale; negative Poisson’s ratio

10.19713/j.cnki.43−1423/u.2019.04.009

TU42

A

1672 − 7029(2019)04 − 0900 − 07

2018−04−12

国家自然科学基金资助项目(51508489)

印长俊(1977−)，男，湖南临澧人，副教授，博士，从事岩土工程研究；E−mail：changjunyin@xtu.edu.cn

(编辑 涂鹏)