用小波变换提高散斑能见度光谱测量法的灵敏度

牟士杭，杨 晖，范彦平，李 然，韩 韧，华云松

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

散斑能见度光谱(speckle visibility spectroscopy,SVS)法是建立在扩散波光谱法(DWS)理论的基础上发展出来的一种用于研究时变动力学(timevarying dynamics)的新方法。该方法有效解决了DWS法不适用于非平稳随机过程的问题。在测量的被动层中会产生许多随机噪声，被动层颗粒温度运动产生的信号较小，加上产生随机噪声，产生信噪比较小的信号，因此要想分析原始信号产生的颗粒温度，提高信噪比并最大限度地提高滤除噪声信号所用的方法非常重要。

近十年来，小波变换在国际上发展迅速并成为热门的研究领域。小波变换能同时进行时间和空间频率的局部化的分析，在时域和频域方面有良好的分辨性，基于多尺度分析理论，在不同尺度下的信号具有不同的局部特征。小波基函数对被分析信号的低频段有着很好的频率分辨率，对高频段有着高时间分辨率；在小波多分辨率理论基础上，把信号携带的信息分解到细节部分，然后得到的细节部分再对其进行分析；连续信号的细节信息和噪声信号的细节信息具有不同的特征[1-4]。

本文利用小波分析的特有属性建立一种低信噪比被动层颗粒温度信号分析的方法，实现颗粒温度信号中噪声的抑制，提高颗粒温度检测精度，以便更好地分析颗粒运动的特征和规律。

1 散斑能见度光谱法原理

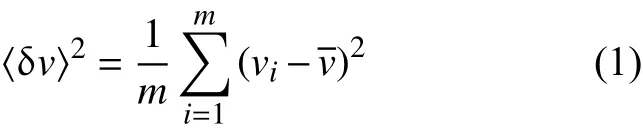
式中：m为粒子的总数；vi为第i个粒子的速度，为所有粒子运动的平均速度。

激光散斑法的原理如图1所示。激光器发出的光通过凹透镜扩散到滚筒中被动层粒子上，然后经粒子间多次散射后，在空间产生干涉现象，发生如图1(b)所示的“散斑”[7]现象。当滚筒转动时，粒子也发生移动，散斑图像产生随机波动，被称为“动态散斑”。计算散斑图像的对比度就可给出测量区域中颗粒位移变化，就能测出颗粒速度波动，即颗粒脉动速度[7]。对于不规则运动的粒子，散斑的波动率和粒子的脉动速度相关，由于线阵CCD照相机上的散斑图像波动随时间变化，就可得到相对应的颗粒速度波动随着时间变化而相应地改变，如图1(c)所示[7-8]。

2 颗粒温度信号小波去噪原理

2.1 小波函数的基本特点

函数x(t)的连续小波变换在所选小波基函数的条件下，其扩展信号为

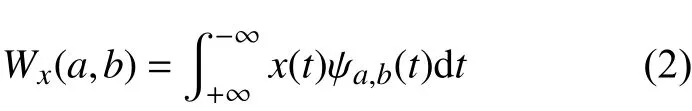
式中：a为尺度因子；b为平移因子；

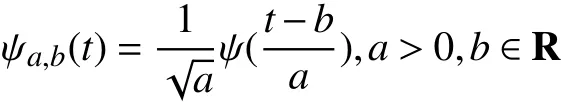
为小波基函数。

由式(2)可知，a和b这两个参数对小波变换有很大的影响。当a很小时，小波更集中于时域，并获得信号细节；当a很大时，小波形状被扩展并且可以获得信号的宏观信息，就有效滤除噪声和得到高不失真信号[9]。

小波变换的反演公式为

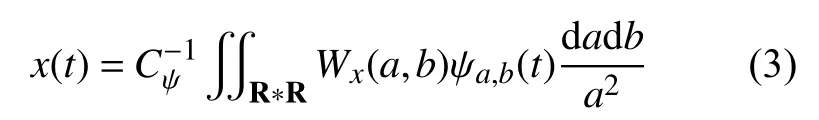
在实际应用的过程中，由于处理的信号绝大部分是经测量信号采集系统得到的离散的数据信号，因此本文将采取小波变换离散形式。

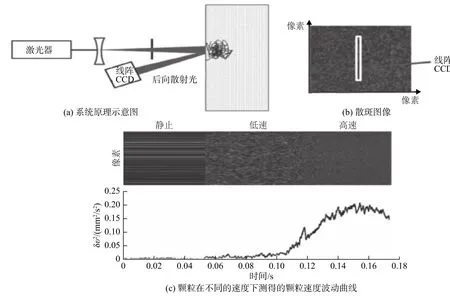
图1 激光散斑法的原理示意图Fig. 1 Schematic diagram of laser speckle method

2.2 小波基函数的选取

目前采用信号检测来确定小波函数的常用方法是最大限度地让小波的波形接近待测瞬态的信号波形[10]。通过实验可以得到，基于小波变换的整个时频域的分辨率分析，DB(Daubechies)小波基函数是一个较好的处理低信噪比颗粒温度信号的方法[10-11]。如图2所示左边为DB12的尺度函数与小波函数，右边是粒子温度信号图，两个图之间具有很强的相似性，都是由小的正弦波组成，具有正交性[10]。

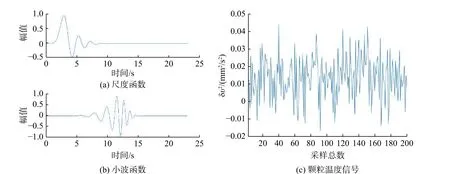
图2 DB12 小波函数与颗粒温度信号对比Fig. 2 Comparison between DB12 wavelet function and particle temperature signal

实际过程中通常需要结合具体情况来具体分析，采用正演与反演的实验方法选择合适的小波函数。本文采用DB N(N为分解层数)作为小波基函数。DB系列小波函数是正交和双正交的，长度为2N−1，滤波长度为2N，消失矩为N。经过数据处理和实验对比，我们可以知道，小波分解层数并不是越多越好。当分解层数超过某数时，许多真实的信号会损失；在分解层数达不到某值时，不能有效地滤除噪声。在实际应用中，分解层的数量应该通过比较峰值信噪比等指标来确定。

3 被动层颗粒温度信号去噪算法的设计

令x0(t)表示在理想条件下被动层粒子温度的瞬态信号，在有噪声n(t)的条件下，粒子温度信号为

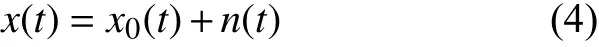
在低信噪比的条件下，对粒子温度信号测量，需从混合信号x(t)中踢除噪声信号，使原始信号被最大限度地提取。

根据采样定理，将x(t)、n(t)和x0(t)分别进行 N点离散化，可得到一个N点序列x(k)、n(k)和x0(k) (k =1,2,···,N)。这样式(4)将变为一个N点序列

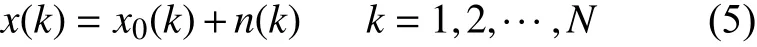
根据小波变换分解原理，采用为Mallat算法分解图。Mallat算法是在基于小波信号分解塔式算法的条件下得到的小波快速算法，其算法在小波变换里的作用与快速傅里叶变换在傅里叶变换中起到的作用是相同的[12-13]。

根据颗粒温度信号与噪声在小波变换下的不同特性，运用的Mallat算法流程图如图3所示[14]，图中G(w)表示低频信号，H(w)表示高频信号。

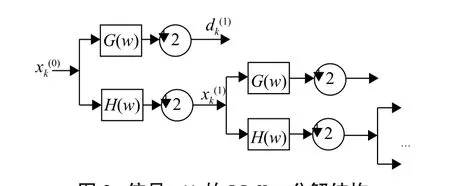
图3 信号 x(t)的 Mallat分解结构Fig. 3 Mallat decomposition structure of signal x(t)

基于小波变换分解原理，采用Mallat小波算法进行分析，基于信号和噪声在小波变换下的不同特征，算法的设计过程如下[15]。

步骤1采用一维小波分析对颗粒温度数据信号进行分解。颗粒温度有噪的信号表示为x(t)=x0(t)+n(t)，x(t)为含噪的颗粒温度信号，x0(t)为真实的被动层颗粒温度信号，n(t)为噪声信号。n(t)为高斯白噪声，正常的情况下是高频信号，x0(t)是低频颗粒温度信号，然后确定一个合适的小波函数并确定分解层数，最后一维分解计算。

步骤2通过小波分析对实测到的粒子温度信号进行分解，得到低频信号与许多高频信号。

步骤3小波分解后对所述颗粒温度数据图的高频信号不变，在这个基础上对分解好的低频信号进行又一次的分解处理，重新获得高频与低频，然后做如下处理[16]：

对所述的颗粒温度信号图小波分解之后的高频部分保留恒定；再线性变换较低分辨率颗粒温度信号，在低频信号的小波系数和数值关系自适应幅度增强条件下，重新得到低频信号。

步骤4小波分解高频系数的阈值量化，高频系数为不同尺度下软阈值所决定的[17]。软阈值去噪法：dm(x)=式中：x为实际测量颗粒温度系数；dm(x)为阈值化分析计算出一维小波系数；sgn为一符号函数；T为阈值，表示为一个软阈值过程。在通常的情况下噪声的特性是按照高斯分布N(0, 1)，在这里阈值T的计算依据为最小均方差的极值方法的恒定阈值，对于噪声未知和非白噪声该方法很适合[10]。此法把不知道的有噪声信号当作和未知回归函数的估计式类似，并且可以使给定函数内最大均方误差最小化，然后对染噪颗粒温度信号降噪处理，并且在处理期间对每一层选择合适的阈值降噪，最后重构信号[17]。

步骤5进行小波重构，小波分解后细节部分低频系数与高频系数再经过小波重构得出处理后的颗粒温度信号[18]。

步骤6根据Mallat重构算法恢复信号并对信号小波逆变换。在噪声抑制后净化颗粒温度信号，对新的低频部分和颗粒温度信号图小波分解之后的高频部分进行小波逆变换以获得处理后的颗粒温度信号图。

4 计算机仿真与结果评估

用计算机仿真时，选择原始信号x0(t)为矩形波，使用不同的小波函数进行模拟比较。选择具有良好正交性与双正交性效应的DB5的小波来分析模拟信号，含噪信号为x(t)=x0(t)+n(t)，信号仿真点数为N=2000，仿真结果如图4所示。图4(a)是一个无噪声的矩形波信号，(b)是在(a)的基础上叠加有噪声的矩形波信号，对(a)和(b)中信号进行傅里叶变换以获得原始方波信号的频谱和含噪声信号的频谱，然后作小波变换。采用DB5小波，作3层分解，用stein自适应软阈值对系数作阈化处理，得到的消噪效果如图4(c)所示。另外，在作傅里叶变换时采取低通滤波器去噪，图4(d)是傅里叶变换去噪的结果图，我们可从图中发现，低通滤波器在除去噪声信号过程中把一些真实的信号给丢失了，滤波器的宽度对去噪效果影响很大。比较图4(c)和(d)可以看出，对于非平稳信号去噪，小波变换的消噪效果优于傅里叶变换效果[19]。

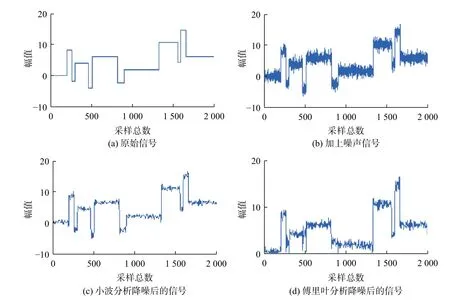
图4 算法在加噪的方波信号中的特性分析Fig. 4 Analysis of the characteristics of the algorithm in the noise-induced square wave signal

5 数据测量与处理

5.1 测量系统的搭建

实验装置如图5所示，滚筒内直径是150 mm其运动是由4个底座固定在滚轴上的驱动轮带动的，用的是德国Dunker公司生产的直流电动机和减速器，通过闭环控制电机带动滚筒以一定的速度转动[7]。在实验过程中用的激光发射器Nova ProDPSS(波长为532 μm，功率为300 mW)是由RGB公司设计的，入射光被一个凹透镜扩展，被一个平面镜反射，并最终入射到圆柱体中被动层中的粒子上，在图中z方向向下的位置，如图5所示[7]。采用的CCD照相机是由DALSA公司设计的，其像素为1024，单个像素的长度是14 nm，最大线速度为68000 Hz，CCD表面配有波长为0.532 nm的滤光片，其作用是去掉周围所带来的无用光[7]。在实验中采用的颗粒是一种规则粒径的0.15 mm玻璃砂[20]。

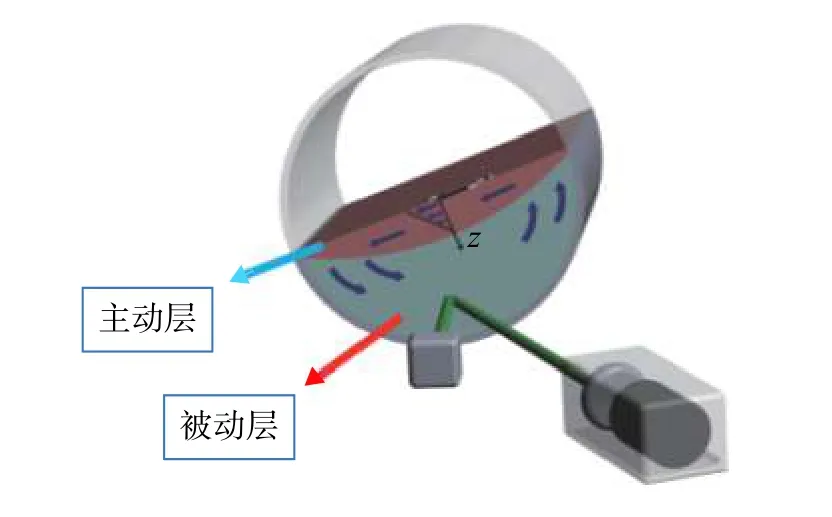
图5 滚筒和 SVS 测量系统示意图Fig. 5 Roller and SVS measurement system structure diagram

滚筒被动层颗粒温度在测量时，会伴随很多其的噪声，从而产生很多无用的噪声加在被动层颗温度数据信号上，尤其是在高噪声环境中，有用颗粒温度信号被噪声信号严重污染[15]，结果使粒子温度测量信号的信噪比非常低，如果利用一般信号处理方法对被动层颗粒温度信号进行检测是非常困难的，因此要引入小波分析来提高系统测精度，以利颗粒温度信号更好的分析与观察[21]。

5.2 实验数据处理与分析

将小波算法应用于被动层粒子信号处理，选取电机电压为0.9 V，图7为经过测量处理得出的含噪声的颗粒温度信号图，即是运用小波变换分解的颗粒温度信号图。选取DB12小波函数族将干扰后的颗粒温度信号进行多层分解，然后再重构颗粒温度信号，经过12层小波分解后，信号波形如图 7所示，图中的 d1，d2，d3，d4，d5，d6，d7是干扰引起的噪声成分，是高频信号。

对图6的颗粒温度信号进行小波变换，再使用软阈值处理法对小波变换后的系数阈值处理，处理后零元素的个数占总元素个数之比为88.04%，去除噪声并重构颗粒温度信号，可得到滤波后的颗粒温度信号。与测量得出的实际颗粒温度信号相比，降噪重构后的颗粒温度信号能量保留成分是实际测量颗粒温度信号的98.4%，而且降噪后得到的颗粒温度信号具有较好的规律性与光滑度，颗粒温度信号分析更方便。

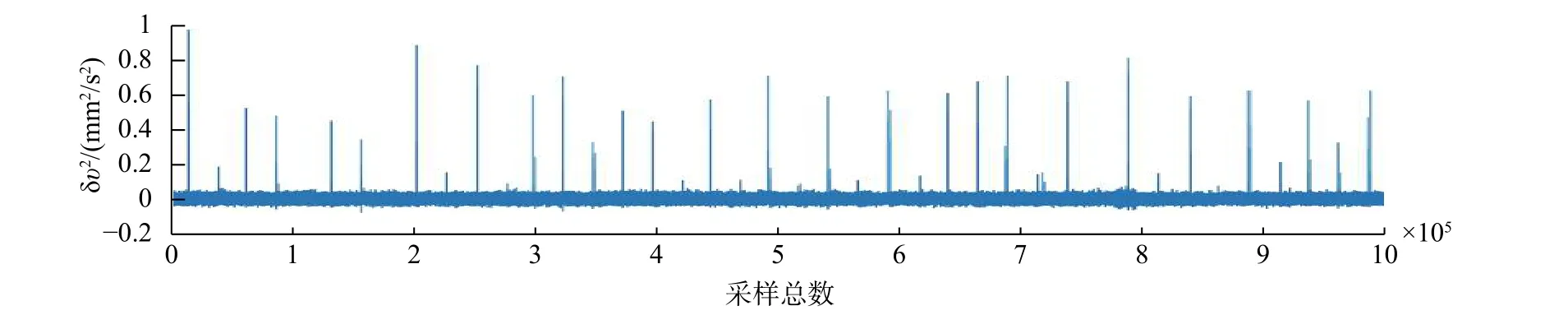
图6 测量得出的被动层颗粒温度信号图Fig. 6 The temperature signal of the passive layer is measured

从图7中d9与d10可以看出，信号有局部突变的变化，此时可以认为滚筒中的颗粒物质运动产生大的转变，即产生崩塌，据此我们就可以准确定位或追踪崩塌的位置。颗粒温度信号的细节部分都集中在a12上，从图形中可以更好地分析被动层中的颗粒温度。如图8所示，降噪后的颗粒温度信号中所包含的颗粒温度瞬时峰值明显降低，由此可以看出有用的信号集中于信号的底部，说明了小波变换可以有效地去除颗粒温度被动层的噪声，使得颗粒温度信号灵敏度得到较大的提高，具有12阶消失矩的DB12小波能够抑制多项式信号成分并且保留大部分测量得到颗粒温度信号有用成分[22]。

在测量实验中可得出，小波基的不同选取对粒子温度信号的去噪有很大的影响。选择不合适时，即使是简单的含噪声信号都不会把噪声信号很好且有效地滤除掉。除此以外，小波分解层数的数量和小波系数的阈值化方法也对去噪效果有很大影响。总之，利用小波变换对被动层颗粒温度信号去噪处理，可以极大地提高信号的信噪比和可检测性，并且在被动层颗粒温度的测量信号处理方面有着非常大的实际应用价值。

6 结束语

准确测量微弱的颗粒运动信号对研究滚筒中颗粒运动具有非常重要的意义。利用小波变换对颗粒温度信号多尺度分解，然后进行细化处理，最后对信号小波重构，得到的结果可最大限度地消除电机所产生的振动和白光所造成的随机噪声。去噪后的效果图能使我们更直观地分析信号，能从细节信号中分辨出被动层崩塌信号的间断点，便于分析与观察颗粒的运动特性，并提高颗粒温度测量系统准确性和精确度。

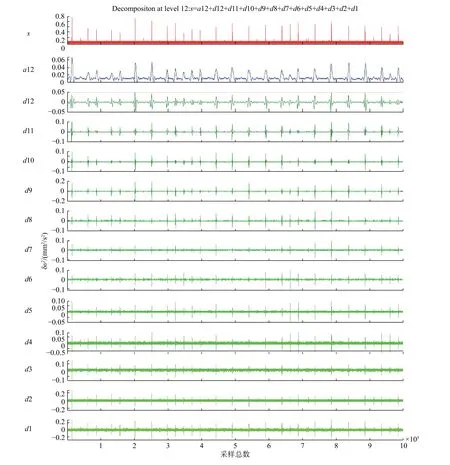
图7 小波分解的层数示意图Fig. 7 The number of layers of wavelet decomposition