工字形三维机织复合材料的弯曲性能
黄耀丽, 吕丽华, 王观桔
(大连工业大学 纺织与材料工程学院, 辽宁 大连 116034)
传统工字形复合材料大都由普通平面材料通过铺层的方式黏合并压制定型而成,虽然制作方法简单,但材料整体性较差,易分层[1]。如果采用机织法直接织造工字形三维机织物,将其与树脂复合制成复合材料后就可解决以上问题。
在工字形三维机织物织造方面,Umair 等[2]织造了T形、H形三维机织预制件,虽然也可织造出工字形三维机织物,但织造完成的工字形三维机织物的高度会受到织机综框数目的严重影响,因此,对于在普通织机上织造高度不受到综框数目影响的工字形三维机织物还需要进一步探讨和探究。此外,张雪飞等[3]、吕丽华等[4-5]在其他异形三维机织物方面也进行了相关的研究。
工字形复合材料是一种在工程应用中常见的结构复合材料。传统工字形复合材料的力学性能受到了广泛的关注[6-8]:Zhou等[9-10]测试了工字形三维编织复合材料的抗冲击、弯曲性能,研究结果表明编织结构对复合材料的应力分布有明显的影响;黄故等[11]测试了工字形三维机织复合材料的弯曲性能发现,工字形三维机织复合材料的弯曲载荷居于较高水平,在中等强度的载荷条件下,不会产生大的变形。同时在结构力学性能分析方面,高雄等[12]分析了不同结构的三维机织复合材料在不同方向上的弯曲性能发现,正交结构的复合材料在各方向上的性能比较平均,总体弯曲性能最好,这也是本文在设计工字形三维机织物时选用正交分层结构的理论依据。目前针对工字形三维机织复合材料弯曲力学性能研究的文献相对较少,其力学性能、破坏损伤模式还需要进一步探讨。
在三维机织复合材料的有限元模拟(FEM)方面,杨萍等[13 -14]采用模拟软件分析了三维编织工字形复合材料的弯曲性能发现,模拟结果和实验结果吻合较好。为外,本文在课题组对其他平板以及蜂窝状三维机织复合材料的有限元模拟及分析研究的基础[15-16]上,选用低价、环保的玄武岩纤维,在普通织机上低成本织造了不同高度的工字形三维机织物,并采用真空辅助树脂传递模塑(VARTM)成型工艺将其与树脂复合制成复合材料,同时对该复合材料进行弯曲性能测试,利用有限元模拟软件对该复合材料的力学性能进行模拟并与实验结果进行对比。
1 实验材料与方法
1.1 工字形三维机织物的设计
工字形三维机织物从结构上来说分为2部分:边缘部分和主体部分,其两端为边缘部分,中间为主体部分。为解决工字形三维机织物的高度在使用普通织机织造时受到织机综框数目限制的问题,本文采用压扁还原法织造了工字形三维机织物,其示意图如图 1所示。具体的经向截面图如图2所示,纹板图如图3 所示。
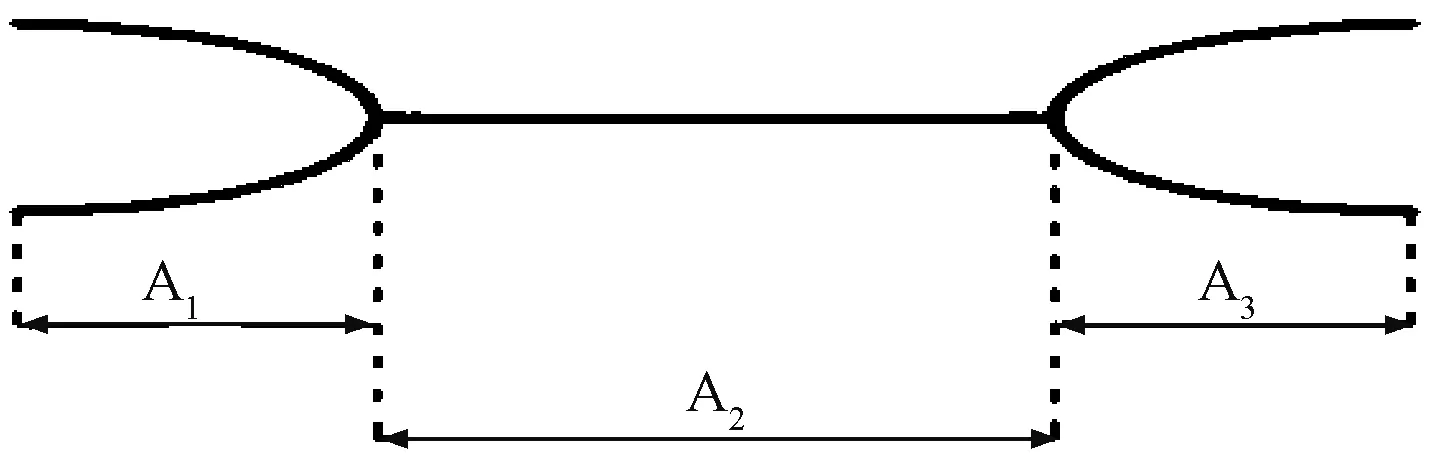
注:A1、A2和A3分别为工字形三维机织物的不同区域。图1 压扁还原法的工字形三维机织物示意图Fig.1 Schematic drawing of I-shaped 3-D woven fabric with flattening reduction method
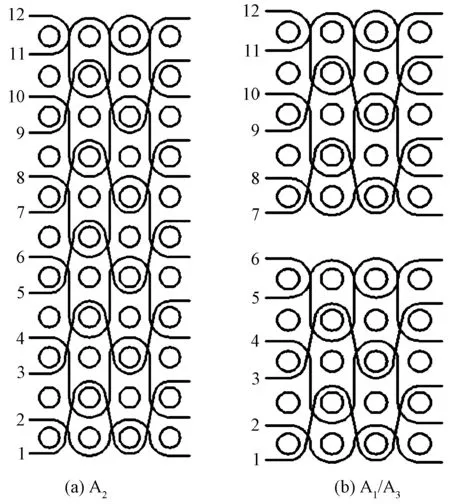
图2 不同高度的工字形三维机织物经向截面图Fig.2 Warp section drawing of 3-D I-shaped woven fabrics with different heights

图3 不同高度的工字形三维机织物纹板图Fig.3 Chain drafts of 3-D I-shaped woven fabrics with different heights
1.2 工字形三维机织物的织造
选用线密度为800 tex的玄武岩纤维(浙江石金玄武岩纤维有限公司)作为经纱和纬纱。采用SGA598型普通织机(江阴市通源纺机有限公司)织造不同高度的工字形三维机织物,织造工艺参数如表1所示。
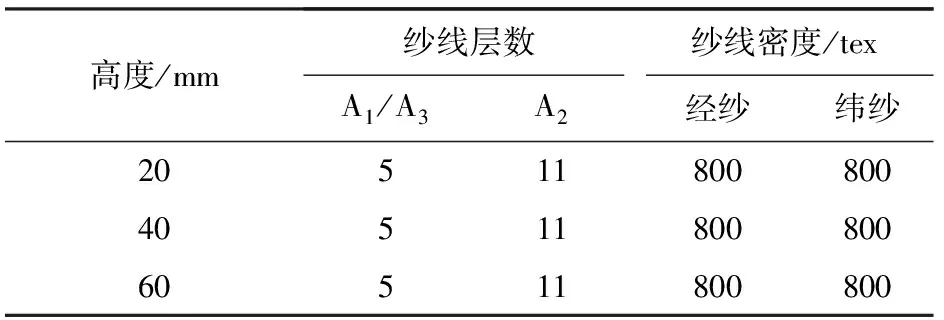
表1 不同高度的工字形三维机织物织造参数Tab.1 Weaving parameters of 3-D I-shaped woven fabric with three different heights
本文实验筘号选用40个/(10 cm)的筘板,总经根数为 720根,织物上机幅宽为150 mm,穿综采用顺穿的方法,穿筘时每筘齿穿12根玄武岩纤维。在织造时,先使用第1块纹板织造A1区,再使用第2块纹板织造A2区,将A2区的织造长度分别控制为20、40、60 mm,最后再使用第1块纹板织造A3区。最后将织造完成的织物进行还原,即可得到 3个不同高度的工字形三维机织物。
1.3 工字形三维机织复合材料的制备
采用真空辅助树脂传递模塑成型工艺制备工字形三维机织复合材料,该工艺操作方便、成本低、室温即可固化[19-21]。本文实验采用环氧乙烯基酯树脂(V118)作为基体,异氰酸酯作为固化剂,三乙醇胺作为促进剂,其中树脂、固化剂、促进剂质量比为400∶5∶5。
1.4 弯曲性能测试
依据GB/T 9341—2008《塑料弯曲性能测试》,将试样制备成长为120 mm、宽为30 mm的样品,在TH-8102S型万能试验机上进行测试,测试速度设为 10 mm/min。最后得到载荷-位移曲线、能量-位移曲线以及弯曲破坏模式图。其中弯曲强度计算公式为
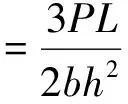
式中:σ为弯曲强度,MPa;P为破坏载荷,N;L为复合材料的测试跨距,mm;b为复合材料试样的宽度,mm;h为复合材料试样的厚度,mm。
1.5 纤维体积分数测试
纤维体积分数是计算与分析复合材料力学性能的一个重要因素,其大小对复合材料的力学性能有较大的影响。本文采用马弗炉燃烧法测定实验制备的工字形三维机织复合材料的体积分数,最终得到高度为20、40、60 mm的3种复合材料的纤维体积分数分别为58.2%、55.2%、53.6%。可以看出随着复合材料高度的增加,纤维体积分数是逐渐递减的。
2 ABAQUS建模与计算
2.1 模型建立
根据实验材料的实际大小,创建3个三维可变形的拉伸实体部件,绘制工字形截面长为 30 mm,梁的厚度为6 mm,上下边缘的宽度为3 mm,高度分别为20、40、60 mm,最后将截面图形拉伸为长度为120 mm的工字形三维实体。
2.2 材料属性设置
在属性设置选项中,添加材料属性参数,主要包括材料的弹性参数和塑性参数。3种不同高度的工字形三维机织复合材料属性如表2所示,表中的材料属性通过反复迭代得到。经过无数次模拟计算后,这组实验数据所模拟的结果和实验测试结果最为相近,所以采用该组数据。

表2 不同高度的工字形三维机织复合材料参数Tab.2 Material parameters of 3-D I-shaped woven composites with different heights
注:E11、E22和E33分别为材料三维x、y、z方向的弹性模量;V12、V23和V13分别为xy、yz、xz平面的泊松比;G12、G13和G23分别为xy、xz和yz平面的剪切模量。
2.3 边界及载荷条件设置
为便于约束条件的设定,将压头与工字形三维机织复合材料模型的上表面进行绑定约束,同时将工字形三维机织复合材料在原有的底座位置(即三点弯曲示意图的底座)进行固定。约束结果为U1=U2=U3=0(U1、U2和U3分别为模拟过程中x、y、z方向的位移)。同时约束其他方向上的自由度为UR1=UR2=UR3=0。添加向下的载荷位移为 -10 mm。分析步设置输出场变量为应力、应变、位移等,输出方式为整个模型;输出历史变量为作用力和反作用力以及位移,且输出方式为参考点。
2.4 网格划分
对工字形复合材料部件整体进行布种,单位设为1,得到3种不同高度(20、40、60 mm)的工字形复合材料的网格总数分别为10 854、15 390、19 602个,并将网格单元类型指派为C3D8R的八节点线性单元。
2.5 提交作业并检查
提交作业并检查,同时可在监控中心进行查看。分析完成后输出并保存材料的载荷-位移曲线以及材料应力分布情况。
3 结果与讨论
3.1 载荷-位移曲线
不同高度的工字形三维机织复合材料的实验及有限元模拟的载荷-位移曲线如图4所示。可知,实验值和模拟值取得了较好的统一性,且在相同位移下,载荷随着复合材料高度的增加而减小。说明弯曲载荷对于该复合材料的高度是敏感的。这是因为当工字形三维机织复合材料在高度较小时,随着材料的受力,弯曲载荷在向下传递时较为迅速且均匀,因此,高度为20 mm的复合材料是整体结构在受力;而随着高度的增加,弯曲载荷的传递变得较为缓慢且不均匀,因此,高度为60 mm的复合材料是材料的上层在受力,所以材料所承受的弯曲载荷随着高度的增加而减小。
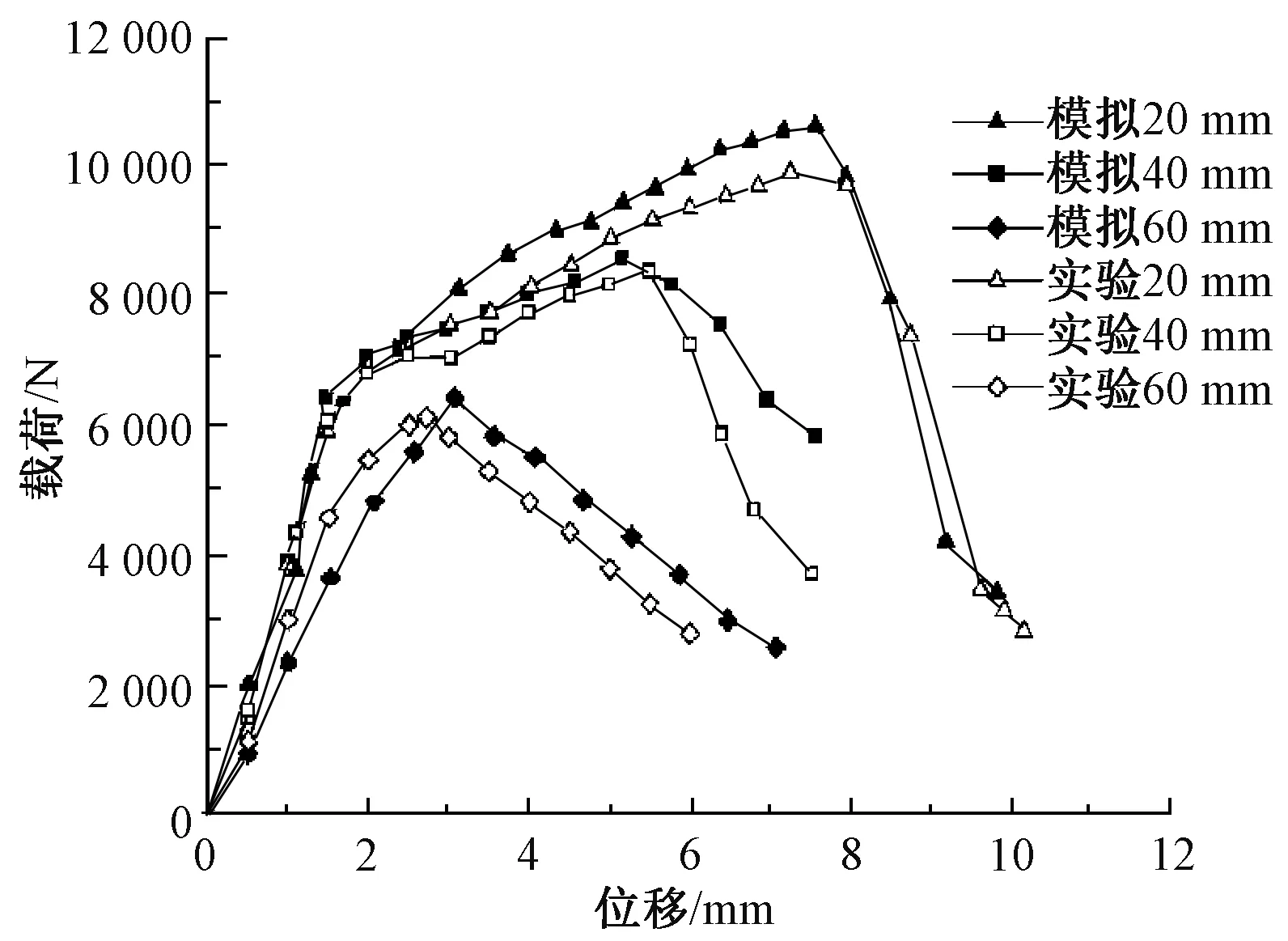
图4 不同高度下的实验及有限元模拟的载荷-位移曲线Fig.4 Load-displacement curves of experiments and finite element analysis with different heights
工字形三维机织复合材料的弯曲载荷-位移曲线大致可分为3个阶段:第1阶段为曲线趋于直线上升的阶段,是因为当压头刚开始与复合材料的表面接触时,材料还未被破坏,随着压头继续向下,位移增加,材料受到的压力也呈线性增长的状态;第 2阶段为曲线小幅度增长阶段,这一阶段产生的原因是随着压头的深入,位移不断增加,材料所受的力也越来越大,达到最大值;第3阶段为曲线趋于直线下降阶段,该部分产生的原因是材料可承受压力的区域已被完全破坏,贯穿阻力减小,因此,载荷随位移的增大而呈线性减小。
工字形三维机织复合材料常作为工程中承重材料,因此,对其弯曲强度和最大载荷的研究是必不可少的。表3示出不同高度下复合材料的实验及有限元模拟的最大载荷误差,表4示出不同高度下的弯曲强度误差。

表3 不同高度下的实验及有限元模拟的最大载荷误差Tab.3 Errors of maximum load of experiments and FEM with different heights

表4 不同高度下的实验及有限元模拟的弯曲强度误差Tab.4 Errors of bending strength of experiments and FEM with different heights
由表3、4可知,不同高度下实验及有限元模拟的最大弯曲载荷和弯曲强度的最小误差为2.3%,最大误差为6.7%,即实验值和模拟值取得了较好的统一性,表明该模型可用来预测不同高度的工字形三维机织复合材料的弯曲载荷。二者之间产生误差的原因可能是:在ABAQUS中假设材料是平滑的,纤维与树脂之间是均匀散布的,网格的划分是均等的,而实验过程中由于种种原因,并不能保证材料中的纤维与树脂之间是均匀散布的。
3.2 能量-位移曲线
能量是衡量材料力学性能的重要指标,因此,在Origin8.5中对载荷-位移曲线进行积分得到材料的能量-位移曲线。图5示不同高度下工字形三维机织复合材料的实验及有限元模拟的能量-位移曲线。
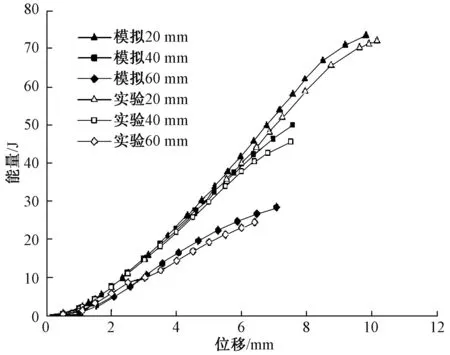
图5 不同高度下实验及有限元模拟的能量-位移曲线Fig.5 Energy-displacement curves of experiments and finite element analysis with different heights
由图5可知,不同高度的工字形三维机织复合材料的吸收能量随着复合材料高度的增加而减小,且实验值和模拟值取得了较好的统一性,说明这一模拟工具可用来预测不同高度的工字形三维机织复合材料的吸收能量。同时,从图5中可以看出,实验结果和模拟结果的总体趋势相同,说明ABAQUS的模拟结果有效且合理。
3.3 破坏模式图
工字形三维机织复合材料在压头作用于复合材料初期时,复合材料主要表现为树脂基体的破坏,材料本身并没有出现严重损伤,材料的承载能力呈现出接近于线性变化趋势。随着压头的继续作用,基体破坏产生的裂纹慢慢扩散到纤维与基体的接触处,以及纤维内部发生脱黏现象。最终纤维发生破坏从而断裂导致材料失效,承载能力瞬间降低。由于不同高度的工字形三维机织复合材料在同一加载速度下,其破坏模式基本相同,因此,以20 mm高度的工字形三维机织复合材料为例,对比分析试样的模拟云图与实验最终形态,如图6所示。

图6 高度为20 mm的工字形三维机织复合材料实验与有限元模拟破坏形貌Fig.6 Photographs of experiments (a) and finite element analysis (b) of 3-D I-shaped woven composites with height of 20 mm
通过对比可以发现,实验和模拟的工字形三维机织复合材料的破坏效果基本相同。从实验破坏图中可以看出,材料出现树脂破裂,部分纤维发生断裂,但并不能明显的看到纤维从材料中抽出来,同时材料并没有出现分层现象。这些现象都说明工字形三维机织复合材料的整体性较好。
根据图6中的破坏形貌图可以看出,工字形三维机织复合材料的破坏主要集中在上下3点,即材料与实验仪器接触的3个点上,上表面表现为压缩破坏,下表面表现为拉伸破坏。同时可以从有限元模拟实验中得到材料在任意时刻和位移的应力云图。
4 结 论
1)通过对织造工艺的合理设计,在普通织机上成功织造了不同高度的工字形三维机织物,并得到一种可以织造高度不受织机综框数目限制的工字形三维机织物的方法。
2)随着工字形三维机织复合材料高度的增加,该复合材料的纤维体积分数、最大弯曲载荷以及吸收能量均是逐渐降低的。当该复合材料高度较小时,材料整体结构受力,弯曲载荷在向下传递时较为迅速且均匀;而随着高度的增加,材料上层受力,弯曲载荷的传递变得较为缓慢且不均匀,所以材料的弯曲性能随着其高度的增加而减小。
3)不同高度的工字形三维机织物的破坏模式基本相同,因此,通过对比高度为20 mm的工字形三维机织复合材料的实验破坏图和ABAQUS破坏模拟图发现,二者具有很好的一致性,验证了该模型使用的可行性,可用该模型推测不同高度的工字形三维机织复合材料的弯曲性能。

