基于无人机热红外的水分胁迫指数与土壤含水率关系研究

尚晓英，张智韬,2，边 江，林历星，李 乐，洪苑琪

(1.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；2.中国旱区节水农业研究院，陕西 杨凌 712100)

0 引 言

作物根系活动层土壤含水率对植物生长、发育有着重要的影响。棉花花铃期是棉花对肥水需求最敏感的时期，是最终产量与品质形成的关键时期[1,2]。所以，基于无人机热红外遥感的水分胁迫指数与土壤含水率的关系研究，对大面积获取棉花花铃期根系层土壤含水率，提高灌溉管理效率以及“精准农业”的发展，具有十分重要的意义。作物水分胁迫指数(CWSI)是一种可靠的作物缺水状况评价指标[3]。关于作物水分胁迫指数(CWSI)的不同计算模式、利用热成像计算作物水分胁迫指数等理论，许多学者已经做出了一定的研究成果。1981年，Jackson等[4]提出了作物水分胁迫指数(CWSI)的定义法计算模式。Jone等[5]在2009年提出了作物水分胁迫指数(CWSI)的简化模式。Bengal等[6]指出土壤含水率与作物水分胁迫指数(CWSI)具有明显的非线性响应。同时，Gonzalez-Dugo等[7]指出作为与气孔相关的作物缺水指标，作物水分胁迫指数(CWSI)在不同灌溉单元之间存在着充足的变异性。Cohen等[8]也指出作物水分胁迫指数(CWSI)相较于植物水分状况的指示器—作物冠层温度，与不同灌水处理的关系更好 。另外，Möller等[9]指出热成像可在未来用于不同作物灌溉调度。Rud等[10]在2014年也提出可以利用基于热成像的数据来计算作物水分胁迫指数(CWSI)。XU等[11]深入分析了CWSI与蒸腾速率、净光合作用、气孔导度的关系。国内蔡焕杰等[3]提出了一种用冠层温度计算作物缺水指标的简化模式。张智韬等[12]分析了不同算法下剔除土壤背景的热红外影像算得的CWSI与棉花叶片气孔导度Gs的相关关系。陈硕博等[13]指出基于无人机遥感可大面积快速获取土壤含水率。这些理论研究成果，在一定程度上为简化作物土壤含水率的获取提供了理论依据，但仍然无法满足精准、简便地大面积获取作物根系层土壤含水率的要求。

本研究借助无人机热红外遥感技术，获取一天中5个时刻的棉花冠层温度，用以算得三种不同计算模式下的作物水分胁迫指数(CWSI)，建立其与不同深度的作物根系土壤含水率的数学模型，并对模型进行验证。研究结果可为大面积实时快速监测作物根系活动层土壤含水率提供一定的理论基础。

1 材料与方法

1.1 研究地概况

试验在陕西省咸阳市杨凌区西北农林科技大学中国旱区节水农业研究院(108°07′E，34°16′N)进行，该试验地位于关中平原腹地，属暖温带大陆性季风气候，年降水量649.5 mm左右，年均气温12.9 ℃。

1.2 试验设计

试验于2017年7月11日至2017年7月15日进行，将该试验区分为12个小区，以灌溉水平不同为依据分4个灌溉水平，分别为：I1(50%田间持水量为上限)、I2(65%田间持水量为上限)、I3(80%田间持水量为上限)、I4(95%田间持水量为上限)，每个灌溉水平有3个重复实验。实验时间为每天的9∶00、11∶00、13∶00、15∶00、17∶00，利用搭载有热红外成像测温仪的无人机获取棉花花铃期的冠层遥感图像，同时利用土壤水分传感器获取0～15、0～30、0～60 cm检测深度上的土壤水分数据。

1.3 冠层温度采集

棉花花铃期冠层温度的采集使用大疆公司与美国FLIR公司合作生产的大疆禅思XT热红外成像测温仪，搭载平台为大疆公司生产的经纬600多旋翼无人机。

1.4 土壤水分及气象数据采集

土壤水分的采集使用北京联创思源公司生产的土壤水分传感器自动收集获得。气象要素主要有：大气温度、相对湿度、风速、净辐射、土壤热通量等，其数据采集与无人机采集冠层温度同步进行。

1.5 计算作物水分胁迫指数

1.5.1 理论模式

根据冠层能量平衡公式(1)、(2)、(3)、(4)可以导出理论模式[9]的CWSIt计算公式(5)：

Rn=G+H+λE

(1)

式中：Rn为净辐射；G为土壤热通量；H为显热通量；λE为潜热通量，单位均为W/m2。

H=ρCp(Tc-Ta)/ra

(2)

式中：ρ为空气密度，kg/m3；Cp为空气热容量，J/(kg·℃)；Ta为大气温度，℃；Tc为冠层温度，℃；ra为空气动力学阻力，s/m。

(3)

(4)

(5)

式中：rcp为潜在蒸散发下的作物冠层阻力，s/m；Δ为饱和水汽压与温度关系曲线的斜率，kPa/℃ 。

1.5.2 简化模式

经过国内外学者的研究，水分胁迫指数的计算需要较多气象因素，给实际应用带来了诸多的不便。因此Jones等[5]又定义了水分胁迫指数简化的计算公式，如式(6)：

(6)

式中：Tl为作物冠层温度，℃；Twet和Tdry分别代表在相同的气象环境中冠层温度的下限和上限，℃。

该简化公式中的参数Twet与Tdry可以通过经验法、理论法、统计法进行确定[6-10,14]。

本研究Twet与Tdry采用经验法，利用自然叶片干湿参考测量计算，具有较高的敏感度[5,8]。在试验的过程中进行两种极端处理，在棉花冠层选取生长良好的叶片，通过给棉花冠层叶片喷水的方式确定Twet，通过给棉花冠层叶片正反面涂抹凡士林确定Tdry。Twet与Tdry的测量与无人机采集冠层温度同步进行。

1.5.3 定义法

根据Jackson导出的水分胁迫指数定义公式(7)，Jackson定义用实际蒸腾速率E比潜在蒸腾速率Ep,即E/Ep可以反映作物缺水状态，则1-E/Ep处在0～1范围内。

(7)

2 结果与分析

2.1 不同计算模式CWSI的变化规律

图1为不同水分处理小区棉花花铃期理论法CWSIt连续5 d的日变化趋势图。从图1可知，棉花水分胁迫指数CWSI受外界气象因素变化而波动，随着冠层吸收净辐射的大小而具有动态日变化过程，其变化过程呈现抛物线形状，并在13∶00时，CWSIt出现极值，且此时的水分胁迫指数CWSIt的差值也达到最大。从图1可以看出，各处理小区随着灌水后时间的推移，水分胁迫指数具有明显的区别。

图2为水分胁迫指数简化模式下不同处理小区连续5 dCWSIs日变化趋势。图2(a)为水分胁迫最为严重的I1处理小区，棉花根系一直处在亏水状态，随着时间的推移水分胁迫指数越来越大，棉花水分胁迫的现象也越来越明显。图2(d)可以看出，I4小区CWSIs每天的差异性较大，I4试验小区为对照充分灌溉组，水分胁迫指数的最大值为0.3，处于较低水平，因此充分供水的棉花受到水分胁迫的影响较小。

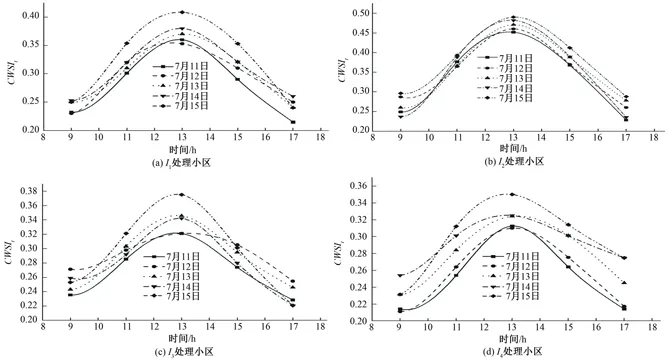
图1 不同处理小区CWSIt日变化曲线Fig.1 The diurnal variation curves of CWSIt in different treatment areas

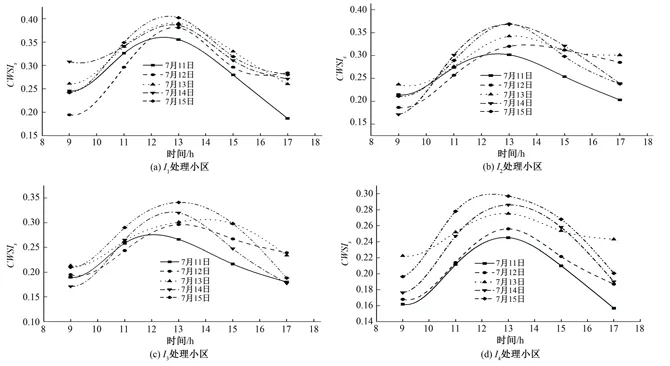
图2 不同处理小区CWSIs日变化曲线Fig.2 The diurnal variation curves of CWSIs in different treatment areas

图3为水分胁迫指数定义法CWSId不同处理小区连续5 d的变化趋势，定义法的日变化规律与理论模式和简化模式相似。

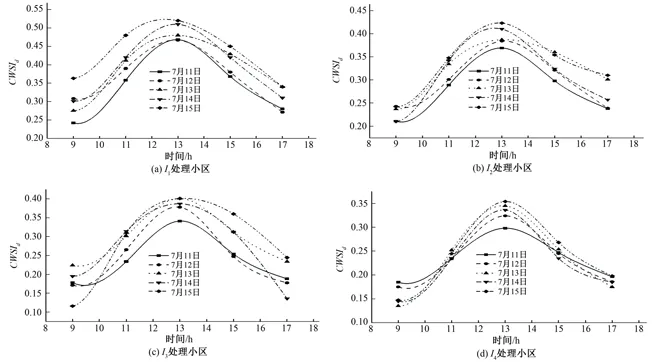
图3 不同处理小区CWSId日变化曲线Fig.3 The diurnal variation curves of CWSId in different treatment areas

图4分别是不同试验处理小区理论模式CWSIt、简化模式CWSIs、定义法CWSId日平均变化过程。从图4(a)中可以看出不同处理小区CWSIt的大致关系为：I1>I2>I3>I4，4种处理水平具有明显的差异性；图中对照组I4小区CWSIt的曲线从0.1一直增大至0.3，其CWSIt变化范围较小，这可以说明当作物充分供水时水分胁迫指数相对偏小，并且波动范围小；I1是缺水处理小区，其CWSIt比其他小区都高，并且最高达到了0.5，说明CWSIt对棉花花铃期根系活动层水分的响应是较为敏感的，随着灌水日期的推移土壤水分不断被作物消耗，CWSIt逐渐上升；图4(b)、4(c)也可以看出不同试验小区的CWSI随时间的变化趋势是增大的，但简化模式CWSIs具有较大的不稳定和波动性，理论模式CWSIt变化速率较快，而定义法CWSId则变化缓慢。

图4 不同处理小区CWSI日平均变化趋势Fig.4 Average daily variation trend of CWSI in different treatment areas

以上分别分析了水分胁迫指数的日变化规律，可知不同模式下的水分胁迫指数的日波动性是不相同的，因此必须深入的研究分析水分胁迫指数的变化规律状况。

2.2 定义法CWSId与不同深度土壤含水率关系

利用公式(7)可以计算得到定义模式下的CWSId，并将CWSId与不同深度的土壤含水率建立相关关系(表1)。

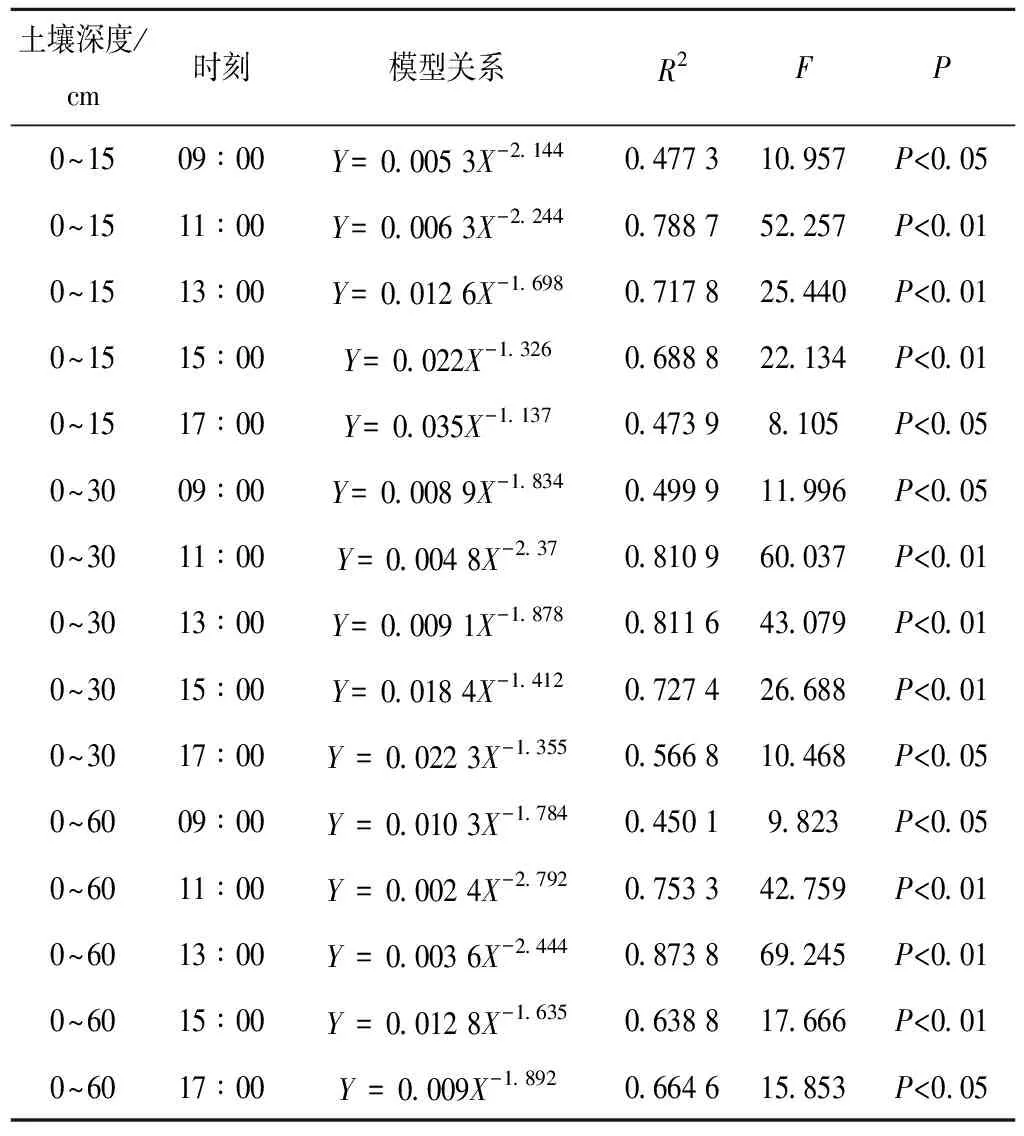
表1 CWSId与土壤含水率相关性Tab.1 Correlation between CWSId and Soil Moisture Content

注：其中Y代表土壤含水率(土壤体积含水率)，X为水分胁迫指数CWSI，以下均同。

由表1可以看出，CWSId与土壤含水率呈现幂函数的关系。CWSId与土壤含水率相关关系在9∶00与17∶00较低，对棉花水分诊断效果不太理想，相关性较高的时刻为11∶00-13∶00，但定义法计算的CWSId与土壤含水率幂函数相关性有一定的波动性和不稳定性。参考13∶00时0～60 cm处的水分胁迫指数与土壤含水率的相关关系,决定系数达到0.87，具有较高精度，在该模型的基础上确定定义法CWSId水分胁迫阈值，本研究设置70%的田间持水量为水分胁迫阈值，因此定义法CWSId在棉花花铃期的水分胁迫阈值为0.20。

2.3 理论模式CWSIt与不同深度土壤含水率关系

利用公式(5)可以计算得理论模式CWSIt，并与不同土壤深度的土壤含水率建立相关模型关系(表2)。

由表2可知，一天中5个时刻幂函数的显著相关性都是在0.01以上，具有较高的稳定性，并且其决定系数都大于0.5。根据理论模式计算得到的水分胁迫指数CWSIt较为稳定，对棉花根系土壤水分的响应敏感，其中13∶00的决定系数是最高的，这与定义法CWSId的结果一致。对比CWSId和CWSIt与土壤水分相关性，可以发现定义法具有非常高的决定系数，但是9∶00与17∶00的相关性较差；理论模式相对于定义法来说，其相关性普遍要低，但理论模式都在0.01水平上显著相关，因此其在反映土壤水分上具有较高的稳定性与可信度，并且误差也会相对较小。理论模式与定义模式都表现与0～60 cm处的土壤含水率有较高的相关关系，且理论模式参考最优模型设置0.18的水分胁迫阈值。

表2 CWSIt与土壤含水率相关性Tab.2 Correlation between CWSIt and Soil Moisture Content

从不同土壤深度的含水率相关性来看0～60 cm>0～30 cm>0～15 cm，可以认为棉花花铃期的根系活动层处在0～60 cm。

2.4 简化模式CWSIs与不同深度土壤含水率关系

利用公式(6)即可计算出简化模式下的CWSIs,表3是简化模式CWSIs与不同深度土壤含水率建立的模型关系。

从表3可以看出，CWSIs与土壤含水率的相关性没有定义法和理论模式的高，但显著相关性也达到了0.01。从不同时刻的模型关系看简化模式与前两种方法的规律一致，相关性较好的时间范围为11∶00～13∶00，根系活动层的主要范围是0～60 cm。依据最优模型关系水分胁迫的阈值为0.24。

从简化模式CWSIs与土壤含水率模型关系可以看出，简化模式响应土壤水分的误差是较大的。

2.5 模型验证分析

本研究的模型关系较多，因此选取3种计算模式与土壤含水率函数关系在13∶00的模型进行分析验证。试验时间为连续5 d，前3 d数据建立函数关系，后2 d数据进行模型的验证(表4)。

从模型验证分析表中可以看出，13∶00时的模型验证决定系数R2均达到了0.5，大田试验的这种验证精度可以满足一定的生产实践需求；其中定义法与理论模式的决定系数R2都是大于0.7的，均方根误差RMSE都在0.02附近，说明定义法与理论模式计算的CWSI具有较高的精度，并且理论模式0～60 cm的模型验证决定系数R2达到0.801，均方根误差RMSE为0.015；3种计算模式中不同土壤深度模型的均方根误差RMSE均呈现出土壤深度0～60 cm<0～30 cm<0～15 cm，说明在棉花花铃期的水分胁迫指数可以很好的诊断0～60 cm土壤深度的作物根系活动层的土壤含水率。综合表中的验证结果可以看出，理论模式精度最高，定义法次之，简化模式最差。

表3 CWSIs与土壤含水率相关性Tab.3 Correlation between CWSIs and Soil Moisture Content

表4 3种模式CWSI与土壤含水率模型验证Tab.4 Three Patterns of CWSI and Soil Moisture Model Verification

3 结 论

(1)棉花花铃期水分胁迫指数与土壤含水率呈现较好的幂函数非线性关系。3种水分胁迫指数CWSI与土壤含水率建立的相关关系中，定义法的相关性最高，但具有较高的不稳定性；简化模式与土壤含水率关系较差；理论模式与土壤含水率有较稳定的关系，可以准确响应作物的耗水状况。对比3种计算模式的模型精度，理论模式最佳，定义法次之，简化模式最差。

(2)棉花花铃期的3种水分胁迫指数对土壤含水率的最佳监测深度为0～60 cm,其次为0～30 cm,0～15 cm最差；对于不同时间点来说，3种水分胁迫指数诊断作物耗水规律的最佳监测时间为13∶00。

(3)利用无人机获取的面状冠层温度极大地提高了棉花根系土壤含水率的反演精度。然而本文只分析了棉花花铃期的水分胁迫指数与根系土壤水分的相关性，其他生育期的规律需要进一步的研究。