雨量站网分布对雨量插值算法及径流响应的影响
汪青静,杨欣玥,陈 华,许崇育,3,曾 强,徐 坚
(1.武汉大学水资源与水电工程科学国家重点实验室,武汉 430072;2.河海大学水文与水资源学院,南京 210098;3.奥斯陆大学地学系,挪威奥斯陆 0317)
1 研究背景
降雨的空间分布对于气象学、气候学、水文学、地质分析、环境监控等都必不可少。现有的降雨数据主要通过雨量站点进行收集,雨量站点能比较精确地测量点降雨,但难以获得大范围的降水分布,时空连续的降雨分布,需要根据已知雨量站点的资料通过空间插值得到。研究表明,降雨的空间分布不均匀性考虑得越充分,其水文过程模拟精度越高[1]。其中不同插值算法、不同雨量站密度会影响降雨空间分布的不均匀性[2-4]。
现有的空间插值方法可以被概括为确定性和地理统计的插值方法[5],在比较不同插值算法时,大多选择交叉验证来比较其降雨插值结果。Driks等[6]用13个雨量站的降雨数据比较了泰森多边形法、反距离权重法、区域平均值和克里金法,他们得出计算复杂的克里金法在结果上并没有明显的提高,建议在雨量站密集的地方使用反距离权重法进行空间插值。高歌等[7]对反距离权重法和普通克里金法的日降雨插值结果进行比较,发现普通克里金法的插值结果略好于反距离权重法。Ly等[8]在分析不同插值算法的日降雨时得到,考虑了高程的具有外部漂移的克里金法和协同克里金法对于日降雨的插值结果并没有提高,普通克里金法和反距离权重法被认为是最好的日降雨插值方法。也有少量研究将插值结果代入水文模型中,根据径流模拟结果比较不同的插值算法。Ruelland等[9]在比较不同空间插值算法对集总式和半分布式模型的敏感性时得到,反距离权重法对于水文模型的模拟较好。综上分析,研究区资料不同,评价指标不同,不能统一得出某种最好的空间插值方法。
通常认为,雨量站数目越多,对降雨的估计误差就越小。然而,由于地形和经济因素的限制,很多地区的雨量站数目和分布都受到了限制。Ruelland等[9]指出在雨量站数目太少时,其插值结果对水文模型的输入误差很大,建议使用雨量站数目较多的区域进行研究。Dong等[10]在研究水文模型对径流模拟最合适的雨量站数目时得到,当雨量站数目到达到一个阈值后,随着雨量站数目的增加,其径流模拟的效果不再增加。Anctil等[11]指出,相比使用所有雨量站的计算结果,合理布设的少量雨量站数目也可以得到较好的计算结果。Xu等[12]研究表明,在雨量站数目较少但空间分布合理时,其水文模型的表现会更好。因此,雨量站网的结构不仅取决于雨量站数目,其分布对于降雨和径流的估计也至关重要。然而现有研究主要分析不同雨量站网情况下的一种或两种插值算法,无法给出不同插值算法在雨量站数目相同时的特定优势。
为比较雨量站网对不同空间插值算法雨量及其径流响应,本文将从以下3个方面展开研究:①在不同雨量站网密度下,不同空间插值算法的雨量误差分析;②在不同雨量站网密度下,不同空间插值算法的径流响应分析;③在雨量站数目相同,但是空间分布不同时,不同空间插值算法的降雨-径流响应分析。
2 研究区域及资料
潇水是湘江上游的一级支流,本文的研究区域为湘江上游双牌站以上潇水子流域。该流域位于24°39′N—26°4′N,111°6′E—112°10′E之间,整个子流域面积是10 434 km2。该子流域高程范围80~1 998 m(图1),流域的西南到东北为沿河平原,东南和西北为山地,高程超过1 000 m。该流域是亚热带季风气候,年均气温在17.6℃,年均降雨为1 600 mm,东部山区降雨较大,可达1 900 mm以上,北部年均降雨较小,在1 300 mm左右。

图1 研究区域高程及气象站点分布Fig.1 Drainage basin delineation and distribution of meteorological stations in the study area
本文研究区内一共有44个分布均匀的雨量站,1个蒸发站,1个流域出口流量双牌站(图1)。这些站点具备流域2006—2014年完整的日尺度数据,均来源于湘江的水文年鉴。
3 主要研究方法
本文先将研究区域离散成1 km×1 km的网格,使用了4种空间插值算法:泰森多边形法、反距离权重法、普通克里金法和协同克里金法,得到研究区2006—2014年所有1 km网格的日降雨序列,对比不同插值算法的降雨误差,再将子流域内所有1 km网格雨量取平均值,得到研究区每日的面均降雨,作为新安江模型的输入,与实测径流对比。
3.1 雨量空间插值方法
(1)泰森多边形法(Thiessen,简称 THI法)[13]将雨量站两两相连并作连线的中垂线,中垂线相交形成与雨量站数目相同的多边形,从而将流域划分成多个多边形(本文共形成44个多边形),每个多边形里面包含一个雨量站,则该区域内的雨量站均用该雨量站的实测值替代。泰森多边形法的优点是计算简单并且使用广泛,缺点是空间插值的结果在多边形内均匀,在多边形边界上突变,这个与实际不符。
(2)反距离权重法(Inverse Distance Weighted,简称IDW法)以插值点与样本点间的距离为权重进行加权平均,离插值点越近的样本赋予的权重越大[14],本文的距离权重指数为2,选择的是距离插值点最近的16个雨量站作为样本点,不足16个样本点的情况则取其所有值。反距离权重法的优点是简单易行,但缺点是易受极值的影响,出现“牛眼”现象[15-16]。
(3)普通克里金法(Ordinary Kriging,简称 OK法)提供了一个在有限区域内对空间变量进行无偏最优估计的方法,其计算公式为

式中:Z*是雨量估算值;Zi(i=1,2,…,n)是实测站点的雨量值;权重λi是根据克里金法的无偏性和估计方差最小计算得到,本文选择指数模型作为拟合半方差的理论模型[17]。
(4)协同克里金法(Cokriging,简称 CK法)将区域化变量的无偏最优估计方法从单一属性发展到两个或者两个以上的协同区域化属性[18]。考虑到降雨和高程的影响,本文将高程作为第2变量考虑在其中,其计算公式为

式中:Z*是估算降雨值;Zi(i=1,2,…,n)是初始变量,即实测站点的雨量值;Ej(j=1,2,…,m)是二级变量,即实测站点的高程值,其权重λi和αj代表初始和二级变量的权重,也是根据克里金法的无偏性和估计方差最小得到。与普通克里金法一样,本文选择指数模型作为半变异函数的理论模型。
3.2 新安江模型
新安江模型[19]是一种概念性降雨径流模型,本文选用的三水源新安江模型在湿润及半湿润地区得到了广泛的认可和应用[12,19-21]。该模型按三水源划分为地表径流、壤中流和地下径流,产流方式为蓄满产流,蒸发分为上层、下层和深层,汇流分为坡地汇流和河网汇流2个阶段,地面汇流采用纳什单位线,壤中流和地下径流采用的线性水库。
本文将研究区的面均雨量站作为雨量输入驱动新安江模型,模拟双牌流量站的径流过程。因为本文目的是比较雨量站网对不同插值算法的径流响应,所以只计算了率定期2006—2014年的日径流量。参数率定采用SCE-UA优化算法[22],以纳什效率系数(NSE)作为目标函数自动搜寻水文模型参数最优解。
3.3 雨量站网密度及分布
为了比较雨量站网密度及分布对不同插值算法的影响,本文选取了6种不同的雨量站网密度(见表1)。其中雨量站最少的情况也满足了WMO在丘陵地区建议的最小雨量站密度[23]。对于前6种雨量站网密度,每次都从44个雨量站中随机选取100种不同的雨量站网分布。Xu等[12]已经证明过,100次随机取样可以代表不同雨量站密度下的区域降雨变化,因此对于每一种插值算法都要计算601次1 km×1 km网格插值结果。

表1 不同雨量站网等级的雨量站数目选取Table 1 Number of rain gauges corresponding to different density levels
对于每一种雨量站密度下的100种不同的空间分布,以空间统计中的最邻近距离指数(NNI)作为选取标准[24-25],NNI常用来刻画点要素的分布格局是集聚、随机还是均匀分布,是根据每个点与最近邻点之间的平均距离计算,其计算公式为:

式中:NNI为雨量站分布最邻近距离系数;d(NN)为雨量站平均最邻近距离(m);d(ran)为期望平均距离(m);di为观测点到第i个雨量站的距离(m);A为流域面积(m2);n为流域内雨量站数目。一般认为,如果NNI<1,则认为雨量站网在空间分布上聚类;如果NNI>1,则认为雨量站网在空间上分布均匀。
3.4 评价指标
降雨和径流是水文模型的两个重要指标,为了比较雨量站网对不同插值算法的降雨径流影响,本文将从降雨和径流2个方面对其插值结果进行比较。
评价降雨精度,一般使用均方根误差(RMSE,Root Mean Square Error),表示插值结果偏离实际值的大小。本文将从点雨量和面雨量2个方面进行分析。点雨量误差分析主要针对于雨量站点实测值与估算值的误差计算;对于面雨量,本文假设44个雨量站插值的面均雨量结果为基准值,而由不同的雨量站密度及分布计算的面均雨量结果作为估算值。基准值与估算值的RMSE越大,则说明插值结果与实测降雨误差大,RMSE越小,则认为插值结果与实测降雨越小,计算公式为

式中:Zest为估测值;Zobs为实测值;n为降雨天数。
评价径流时,将不同雨量站密度及分布的面均降雨代入新安江模型中计算,根据纳什效率系数NSE比较其径流模拟精度。
4 结果及分析
4.1 雨量空间分布规律分析
本文选用了4种经常使用的空间插值算法,因为这4种插值算法代表了不同的降雨空间分布,也考虑了不同的降雨属性。图2给出了4种插值算法在使用44个雨量站时的年均降雨插值结果,从图中可以看到,反距离权重法、普通克里金法、协同克里金法的插值结果相似,泰森多边形法的降雨插值结果在空间上分布不连续。但是不论对于哪一种插值算法,都能从其年均降雨的空间分布中得出:在流域的东边和西边,其年均降雨量较大。
4.2 不同雨量站密度下不同插值算法的雨量误差分析
对于不同插值算法的雨量误差分析,本文将从点雨量和面雨量2个方面进行分析。点雨量误差分析是计算雨量站点实测值与估算值的RMSE。根据前人的研究,交叉验证正被广泛地使用[26-28]。针对本文使用的4种插值算法,在使用不同雨量站密度和分布插值时,将剩下来的雨量站(以研究区总共44个雨量站减去使用的插值雨量站)实测数据作为基准值,与4种插值算法所计算的点雨量估算值进行比较,使用RMSE作为评价标准,然后对剩下来雨量站的RMSE取均值,得到每种雨量站分布的点雨量插值误差。图3是这6种不同雨量站密度100次随机分布下4种插值算法所计算RMSE的箱线图。从图3中可以看到,对于这4种插值算法,其RMSE都是随着雨量站数目的增加而减小,说明随着雨量站数目的增加,其降雨的插值误差也越来越小。同时,反距离权重法、普通克里金法、协同克里金法的点雨量误差范围及趋势基本相同,但是明显的小于泰森多边形的点雨量误差范围,这是受泰森多边的插值原理所致,说明泰森多边形的插值结果与实测值偏离较大。
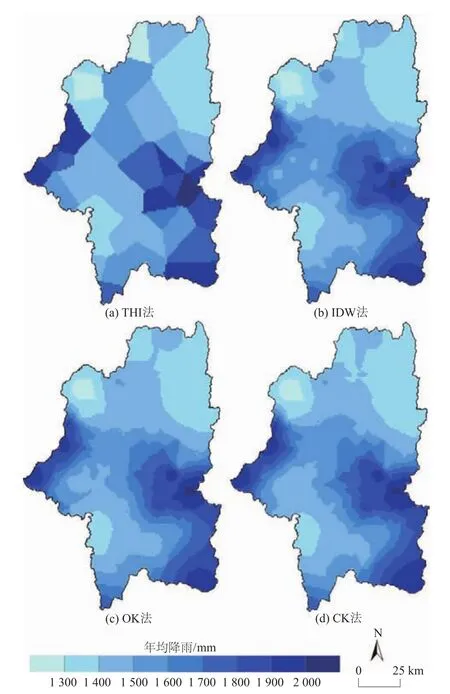
图2 4种不同插值算法在2006—2014年的年均降雨插值结果Fig.2 Interpolated average annual rainfall for 2006-2014 obtained by four spatial interpolation methods

图3 不同雨量站密度下100次随机分布的雨量站点间实测值与估算值的RMSE的箱线图Fig.3 Box plot of RMSE of observed and estimated daily rainfall in the presence of different densities of rain gauges in 100 stochastic samplings for each number of stations respectively
区域的面均雨量是新安江模型的一个重要输入项,而不同插值算法在雨量站密度及分布相同时也会得到不同的面均降雨。图4给出了这4种不同插值算法的面均雨量基准值与估算值的RMSE。
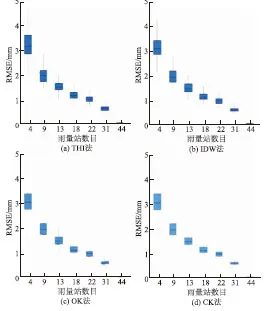
图4 4种插值算法2006-2014年的日均降雨在不同雨量站密度下100次随机分布的RMSE箱线图Fig.4 Box plot of RMSE of observed and estimated average daily rainfall in 2006-2014 in the presence of different densities of rain gauges in 100 stochastic samplings by four interpolation methods
从图4中可以看到,对于这4种插值算法,随着雨量站数目的增加,其RMSE的值越小,其RMSE的误差范围也越小。
综合点雨量和面雨量的分析得到:对于任一种空间插值算法,随着参与计算的雨量站数目的增加,其降雨插值结果误差越小。
4.3 不同雨量站密度下不同插值算法的径流响应分析
将不同雨量站密度及分布计算的面均雨量代入到新安江模型中,计算其径流模拟的纳什效率系数NSE。从图5可以看到:①随着雨量站数目的增加,模型的NSE范围逐渐减小,并且NSE也会随着参与计算的雨量站数目的增加而增大,但当雨量站数目增加到一个阈值时,4种插值算法的NSE范围逐渐减小并趋于一个稳定值(即使用44个雨量站时所达到的NSE);②泰森多边形法在使用4个雨量站插值时,其NSE的范围明显大于其他3种插值方法,当参与计算的雨量站数目增加时,这4种插值方法的NSE结果差别不大。

图5 不同雨量站密度下100次随机分布的插值结果代入新安江模型中的NSE箱线图Fig.5 Box plot of Nash-Sutcliffe coefficients of Xinanjiang modelling calculated from different rain gauges’density for four different interpolation methods
由于本文是将研究区离散成空间上1 km网格计算日降雨,再取平均值得到面均雨量后代入新安江模型,当雨量站数目较少时,不同插值算法的面均雨量波动均较大,其中泰森多边形法的面均雨量波动范围更大(见图4(a)),新安江模型受不同插值算法的水量输入影响较大,所以NSE波动范围也较大;随着雨量站数目的增加,4种插值算法计算的面均雨量差异逐渐减小,新安江模型受不同插值算法的水量输入影响较小,因此在雨量站数目达到某个阈值后,其NSE变化范围很小。Xu等[12]也得到了相似的规律,他指出当雨量站数目达到一定后,新安江模型径流模拟的NSE变化范围较小。
4.4 相同雨量站的不同空间分布对插值算法的降雨-径流响应分析
本文选取了前面6种不同雨量站密度(表1),每一种密度都有100种不同的分布,根据NNI指数的最大和最小值,选出这100种随机分布下最均匀(Best,以B表示)和最不均匀(Worst,以 W表示)的2种分布,并列出这12种不同的雨量站空间分布(图6)。从图6中可以看到,无论在哪种雨量站密度下,NNI指数最大时,其得到的雨量站在整个研究区空间分布均匀;而NNI指数最小时,其得到的雨量站在整个研究区空间分布聚集。所以,NNI指数大的雨量站空间分布会明显好于NNI指数小的空间分布,因此将NNI指数作为本文定量描述雨量站空间分布的一个标准值。

图6 6种不同雨量站密度下由NNI指数得到的雨量站空间分布Fig.6 Spatial distribution of rain gauges selected by NNI of six density levels
针对上述12种雨量站的空间分布,计算本文4种插值算法间的点雨量误差RMSE(图7(a))。从直方图中的RMSE可以看到:①对于这4种插值算法,雨量站均匀的RMSE明显要小于雨量站分布不均的RMSE,这说明,雨量站的空间分布越均匀,其降雨插值的误差也越小;②对于任何一种雨量站分布情景,泰森多边形法的RMSE明显的要高于另外3种插值方法,而其中普通克里金的RMSE和协同克里金的RMSE结果非常相似,稍好于反距离权重法的RMSE,说明对于点雨量的估计,考虑了空间变量的克里金法(普通克里金和协同克里金)对日降雨的估计较为准确。

图7 不同雨量站分布下4种插值算法计算的RMSE和NSE的柱状图Fig.7 Histogram of RMSE and NSE in different distributions of rain gauges using four different interpolation methods
再将4种插值算法计算的12种雨量站分布的面均雨量代入新安江模型计算其径流模拟系数NSE(图7(b)),从直方图中的NSE可以看到:①随着雨量站数目的增加,当雨量站数目达到某个阈值后,不论站点分布是否均匀,这4种插值方法所得到的NSE差异逐渐减小,这也从雨量站密度分布的个例分析中证明了图5的结论;②当雨量站点分布均匀时(图7(b)中横坐标B表示的部分),这4种插值方法的径流模拟系数NSE差别较小,说明在雨量站网布设均匀时,各空间插值算法插值结果差异较小;当雨量站点分布不均匀时(图7(b)中横坐标W表示的部分),在雨量站数目较少时,不同插值方法所得到的NSE差异较大,而随着雨量站数目的增加,不同插值算法的NSE差异减小,说明在雨量站网布设不均匀时,站点数目越少,各空间插值算法插值结果差异越大。
综合考虑图7,针对这4种不同的插值算法,在计算点雨量时,考虑空间变量的克里金(包括普通克里金和协同克里金)插值算法要稍好于反距离权重法,明显好于泰森多边形法,所以对于估算单个雨量站点雨量或者分布式水文模型的雨量时,泰森多边形法不能很好地估算实际降雨,克里金法相较于反距离权重法能更为准确的估算日实际降雨;在计算面均雨量时,由于对流域所有网格取面均值后,不同插值算法间差异较小,因此可以选用计算简便的插值算法,比如泰森多边形、反距离权重法。
5 结 论
本文在雨量站密度及分布不同情况下,比较了4种常用的空间插值算法的日降雨结果,并将面均降雨带入水文模型中比较其径流的纳什效率系数,得出结论如下:
(1)对于任一种空间插值算法,随着参与计算的雨量站数目的增加,降雨插值结果误差也减小,其径流模拟的纳什效率系数会先增大,到达一个阈值后不再明显变化。
(2)在雨量站数目不变时,雨量站空间分布越均匀,雨量插值的结果误差也越小,其径流模拟的纳什效率系数也越大。
(3)在雨量站网布设均匀时,各空间插值算法插值结果差异较小;在雨量站网布设不均匀时,站点数目越少各空间插值算法插值结果差异越大。
(4)在计算点雨量时,考虑空间变量的克里金(包括普通克里金和协同克里金)法要稍好于反距离权重法,明显好于泰森多边形法,因此克里金法能更准确地估算日降雨;在计算面均雨量时,不同插值算法间差异较小,可以选用计算简便的插值算法。

