基准转换参数求解方法研究

葛露露， 顾和和

(1.安徽水利水电职业技术学院，安徽 合肥 231603; 2.中国矿业大学， 江苏 徐州 221116)

不动产登记需要大量的不动产数据,这些数据由各个不动产部门提供,它们有自己的数据采集标准。通常采用最小二乘法[1]求解不同基准之间的转换模型参数。但是,最小二乘法具有局限性,因此,考虑采用稳健估计的方法求解转换模型的参数,并用实例验证。

1 参数求解方法

1.1 最小二乘法(LS)[2]

该法是测绘行业最为常用的一种模型方法,其中高斯-马尔科夫(G-M)模型最经典。在系数矩阵B中不含有误差的前提下利用G-M模型求解,该模型没有顾及系数阵中含有的误差,仅考虑L中的偶然误差,V为残差向量,最小二乘原则:

VTPV=min

(1)

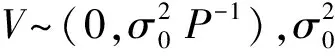
(r为多余观测数)

(2)

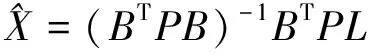
(3)

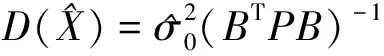
(4)

G-M模型简单容易理解和掌握,但G-M模型求解参数没有顾及可能含有粗差的情况, 只考虑了L中有偶然误差,一旦含有粗差,求解的参数偏差较大,无抗差性[3]。

1.2 降权法

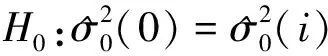
(5)

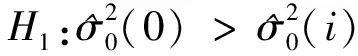
(6)

对其进行Fi检验:

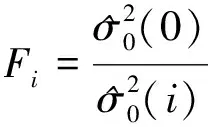
(7)

Fi服从F分布,其显著水平为α,对应的自由度为r1,r2,即:

Fi～F1-α(r1,r2)

(8)

4参数模型的自由度为:r1=2n-4,r2=2(n-1)-4,n为参加计算的点的个数。

由于出现可靠数据低于3个时不能进行方差比值法检验,所以对特别明显的粗差才直接剔除,不是非常明显的粗差则降权处理,用不同的2个显著水平不同作为区分不同程度同的粗差,令α1<α2,α1用来区分特别明显的粗差,α2是用来能够发现粗差的水平,位于α1与α2之间的数据可能是粗差:

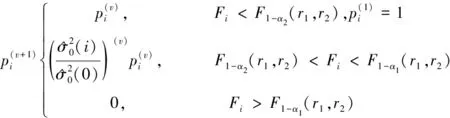
(9)

其中，(v)代表的是迭代的次数,通过之前大量的实验得出当α1=0.05,α2=0.35[5]时效果比较好。

1.3 降权最小二乘法

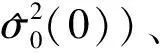
2 实 例

使用LS法和降权LS法,分别求解4参数模型参数,并对求解精度进行比较。表1是2套坐标系中点的坐标值, 1-8号点粗差未知的基准点,9、10号是不含粗差的检核点。

表1 2套坐标系的坐标

构建模型:

V=BX-L

求解缩放尺度κ、旋转参数α、平移参数a、平移参数b及单位权方差,结果如表2所列。

表2 求解的参数及单位权

由表2可见,LS法的单位权方差的精度要低于降权LS法的单位权方差精度。利用求出的两组参数进行坐标转换,将原坐标系中的重合点(包括转换基准点和检核点)利用求出的转换参数求解,用式(10)将目标坐标系中的坐标与求解的坐标进行相减,获得坐标残差值,再利用式(11)计算转换点和检核点的点位中误差,如表3所列。

Δxi=Xi-xi,Δyi=Yi-yi

(10)

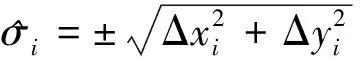
(11)

LS法受到粗差的影响,转换点位误差在0.7m-0.8m,降权LS法求解的点位精度在0.01m-0.03m。

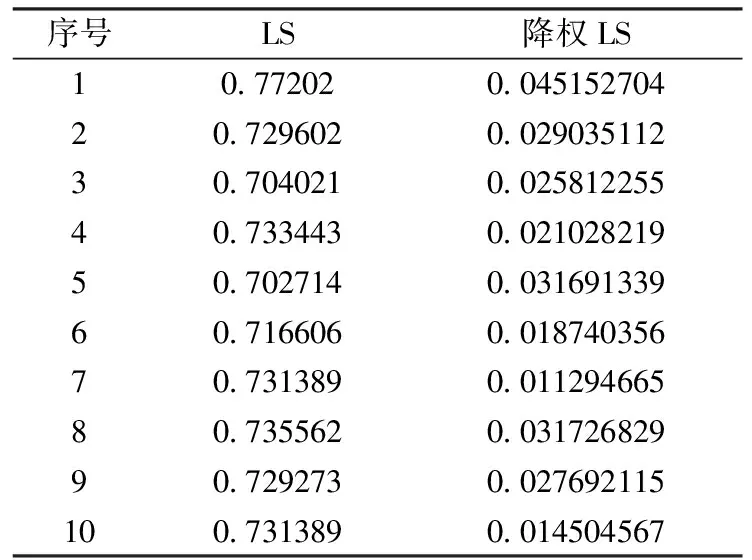
表3 各点的点位中误差

据转换基准点和检核点的点位中误差,计算内符合精度、外符合精度。假设有n1个基准转换点(如果剔除点则要把剔除的点减掉),n2个检核点,计算内、外符合精度公式如下:

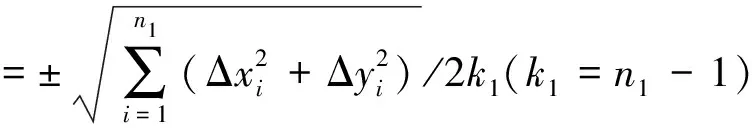
(12)

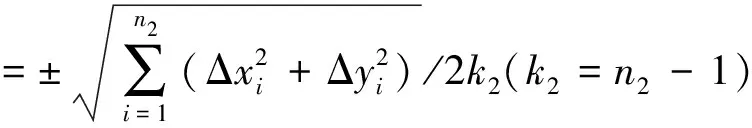
(13)

LS法求解的内、外符合精度为:55cm、 73cm,降权LS法求解的内、外符合精度为:1.2cm、2.2cm,其精度较LS法提高很多。

3 结束语

本文对求解坐标之间的转换参数的求解方法进行了分析,并以4参数模型为例进行了演示,通过对4种不同参数求解方法的精度比较,可以发现如果数据中含有粗差LS法、TLS法不能得到可靠的参数解,但是采用降权方法可以得到较为可靠的参数解。本文仅以4参数模型为例,有可能存在一定的局限性,参数的求解精度还和选择的模型、点的分布均匀情况等相关。