从培养学生科学思维的视角例谈数模建构
朱淑芳
(福建省漳州市第五中学 漳州 363000)
在教学中渗透科学思维能力的培养尤为必要,而数学模型作为揭示生命现象的特殊的呈现形式,是将原型的本质特征用数学语言构建而成的逻辑严密的数学过程或符号。本文以数模建构为抓手,引导学生进行改造、修正和完善,在建模、析模过程中达成思维的有序展开,使数模建构成为培养学生科学思维能力、提升生物学核心素养的有效途径。
1 改造模型,促成知识内化升华,培养批判性思维
批判性思维能力是能够质疑、解释、分析和自我校准的能力[1]。数学模型是对生物学知识的精练简化,往往是学生解释分析问题的重要载体。在建模过程中,引导学生提取原有模型承载的知识信息,深挖掘、细分析,在新的条件下完成模型改造,让被利用的先前知识根据具体情境的变异性得以重新建构,实现原有知识的内化、升华,让学生在思维碰撞和问题解决的过程中,提升批判性思维的能力。
例如,学生对捕食关系的数学模型的认知是以种群数量和时间建立起来的坐标图(见教材第73页“资料分析”中“猞猁和雪兔种群数量的变化曲线”)。在这个模型里承载着这样的信息: 被捕食者和捕食者之间呈现“先增加者先减少,后增加者后减少”的不同步变化。在授课过程中,鼓励学生转变思维,对该模型进行改造: 构建以被捕食者种群数量为横坐标,以捕食者种群数量为纵坐标的新模型(图1)。构建后,设置问题进一步自我校准: 若将封闭环以P2为横轴、N2为纵轴,划分为①②③④共4个区间,每个区间分别对应原坐标图中的哪个区段?改造后的模型能体现“先增加者先减少,后增加者后减少”这种变化规律吗?同时,可引导学生对错误观点“P3代表捕食者的K值,N3代表被捕食者的K值”提出质疑并进行解释分析: 从图1封闭环的变化趋势可以看出,捕食者和被捕食者在相互作用过程中,数量在N2和P2水平上保持动态平衡。所以,P2和N2才是捕食者和被捕食者的K值。
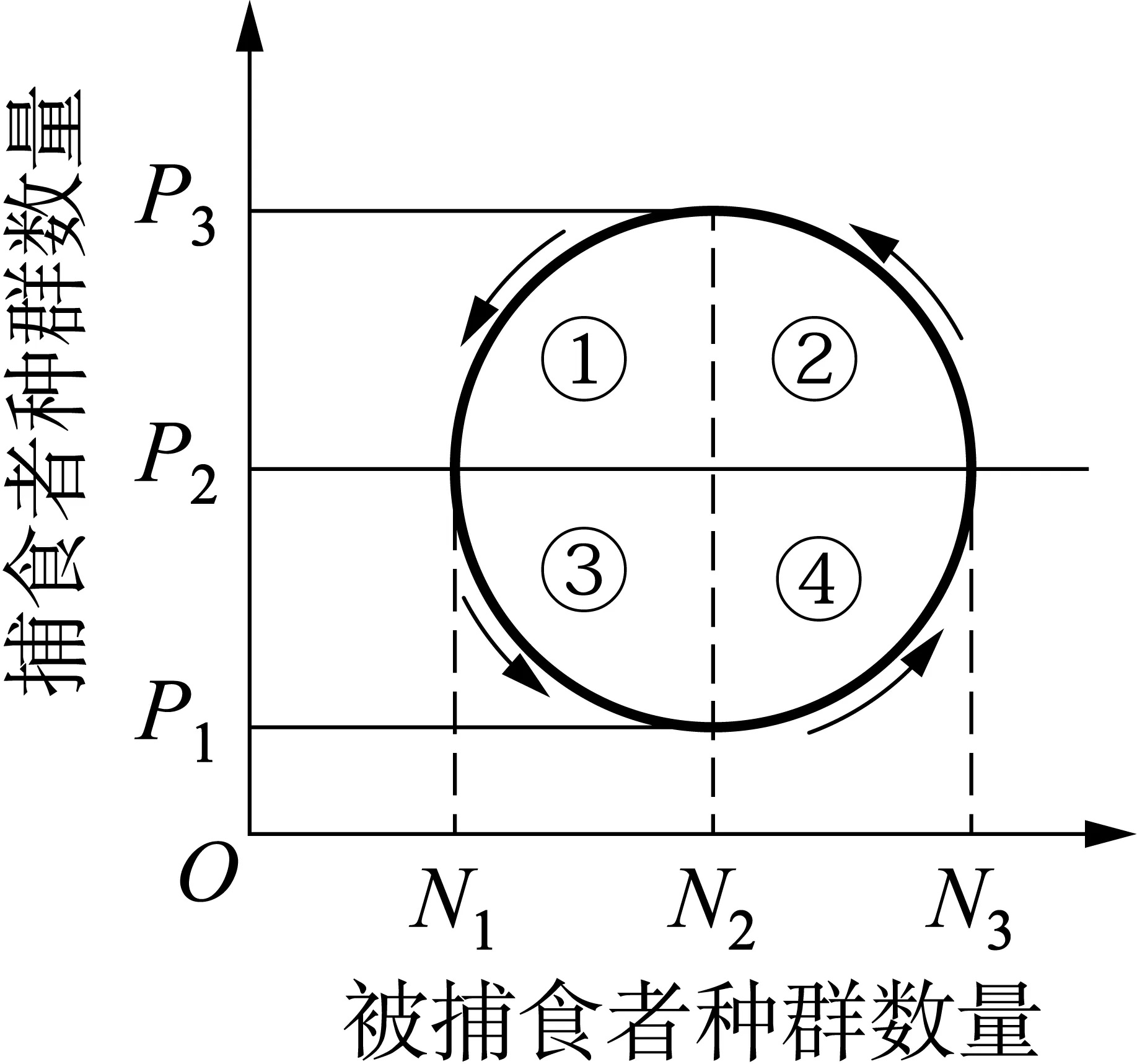
图1 捕食者和被捕食者种群数量变化关系
综上可见,在对模型的改造重建过程中,伴随着对问题的抽丝剥茧,理性的辨析使学生在熟悉内容和陌生问题间实现有效转化升华,促成思维迁移和问题解决,一定程度上培养和锻炼学生的批判性思维。
2 修正模型,实现技能迁移应用,提升演绎推理能力
演绎推理是以一般性知识判断为前提,推出个别的、具体的知识结论的推理过程,是重要的科学思维方式[2]。众所周知,学生对于遗传学“杂合子Aa(亲代)连续自交,求第n代基因型的比例”“Aa连续自交并逐代淘汰隐性个体,求第n代基因型的比例”这类经典问题常望而生畏。但由于其推导过程所涉及的建模方法是突破有关基因分离定律某些重点题型的好方法,也是培养学生演绎推理能力的有效“推手”,所以一直很受关注。
例如,在分析这类题型时,引导学生从正常情况展开建模,即逐代写出Aa连续自交(不淘汰)时各基因型的比例(F1代: 1/4AA,1/2Aa,1/4aa;F2代: 3/8AA,1/4Aa,3/8aa……),分析至F3代,依据规律便可构建出相应的函数模型: 第n代杂合子的比例等于(1/2)n。在这基础上,结合设定的限制条件(逐代淘汰隐性个体),引导学生沿着原有思维轨迹继续推理分析时就会发现: 逐代淘汰隐性个体会影响到每一代非隐性个体基因型在总群体中所占的比例(图2),这时学生自然会领悟到: 当原有模型已经不再适用于新情境时,就必须结合新信息给予修正,在思辨过程中演绎推理出正确的模型: Aa连续自交(淘汰隐性个体),第n代杂合子的比例应为2/(2n+1)。
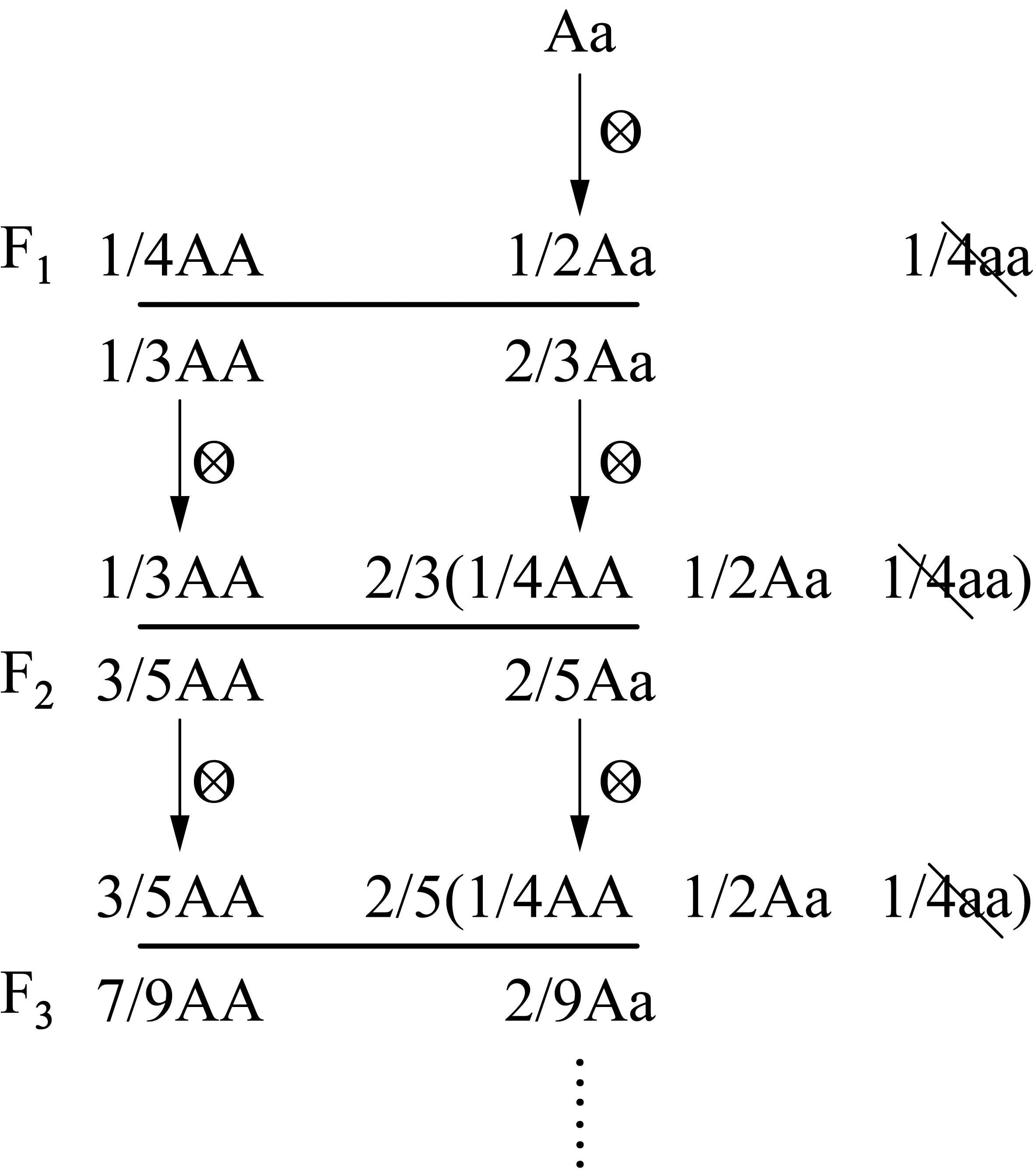
图2 Aa连续自交(淘汰aa)后代基因型频率的变化
在模型的修正过程中,促成了学生从一般规律的理解应用到学会运用新规律来检验、巩固新知识的飞跃,不仅实现了数学知识技能在生物学领域的迁移应用。同时,也让学科素养和能力培养在建模过程中得到渗透和提升。
3 完善模型,达成知识迁移拓展,提高概括归纳能力
数学模型可以用来描述事物本质和变化规律,在组织教学过程中,教师可有意识地引导学生对模型进行完善充实,不仅扩充了模型的知识承载量,同时也培养了学生透过现象揭示本质的洞察力和对事物变化规律的准确概括归纳能力[3]。
例如,在教材(必修2)“孟德尔豌豆杂交实验(一)”一节“性状分离比”的模拟实验中,教材只要求完成一组模拟实验并设计相应的数据统计表(表1)。在这个实验中,模拟雌雄生殖器官的甲乙两袋内D配子和d配子数量相同(均为15个),且甲乙两袋内配子总数相等(均为30个)。但单纯完成这组模拟实验,并不能有效达成体验孟德尔假说、理解分离定律实质的目的。因此,设置如下问题: 如果甲乙两袋内D、d配子数相同,但两袋内配子总数不同,对实验结果有影响吗?如果甲乙两袋内D、d配子数不同,但两袋内配子总数相同,又会产生什么样的结果呢?引导学生根据问题进行拓展实验并完善原有图表模型,最终获得另外2组数据(表2、表3)。
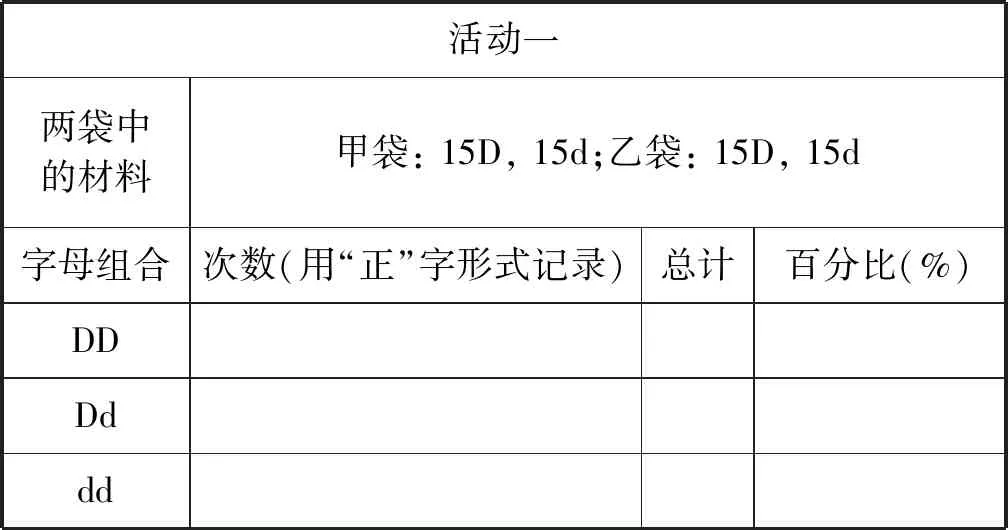
表1 孟德尔性状分离比模拟实验小组记录数据统计表(活动1)
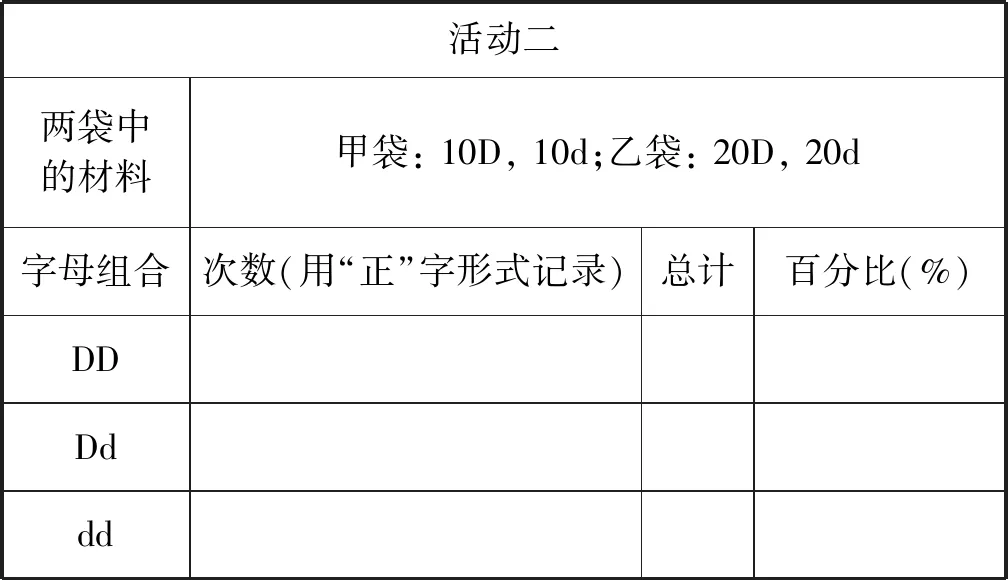
表2 孟德尔性状分离比模拟实验小组记录数据统计表(活动2)
表3 孟德尔性状分离比模拟实验小组记录数据统计表(活动3)
通过数据处理、模型(3个统计表)对比和归纳分析,学生会发现,活动1、 2的数据统计结果DD∶Dd∶dd接近于1∶2∶1;而活动3中该数据远偏离1∶2∶1。
学生很快会意识到形成3∶1性状分离比的关键之一是杂合子产生的2种不同的配子比例要相等,进一步厘清了分离定律的实质。

