峡谷区岸坡岩体渗透性分布规律浅析
彭 佩
(芜湖职业技术学院建筑工程学院,安徽 芜湖 241000)
1 引言
我国目前在建的大型水利水电工程主要分布在西南高山峡谷地区,并且根据国家水电建设规划还将在雅砻江、金沙江、大渡河等流域陆续建设多个水电工程项目,到2020 年总装机容量将达到2.1 亿kW 以上。位于这些峡谷区的水电站工程由于受构造运动和特殊地质环境的影响,其工程地质及水文地质条件具有显著的区域特征:(1)岸坡陡峻,呈深切“V”型峡谷,坡度可高达70°;(2)地质构造环境复杂,大范围发育有深卸荷破碎裂隙带;(3)区域天然地应力较高,处于高~极高的地应力环境。因此,峡谷区岸坡岩体渗透特性分布特征的研究,对于水电工程渗透稳定分析和渗控效果评价具有十分重要的意义。
由于岩性和破碎岩块块度的差异,岸坡岩体渗流常常会表现出明显的成层性和分带性,总体上呈现出明显的壳状渗透结构,主要表现在渗透性会随岩体埋深的增加以及风化卸荷程度的减小而逐渐减弱。Lousi[1]在1974 年根据钻孔压水试验数据证实了岩体的渗透系数确实随深度的增加而减小。随后Neuzil[2]等在1986 年研究了孔隙类岩体渗透特性随深度的变化规律。此外,国内不少的学者通过对裂隙岩体钻孔压水试验数据进行统计分析,研究了岩体埋深与其透水性之间的关系:周志芳等[3]分析了紧水滩水电站坝址花岗岩、石塘水电站坝址火山凝灰岩的水文地质资料,发现岩体的渗透特性随深度增加而明显减弱的规律。张琦伟等[4,5]采用指示克里格方法,以指示变异函数为基本工具分析了向家坝水电站裂隙岩体渗透特性的分布规律。蒋小伟等[6]利用我国西南某水电站的压水试验资料分析了玄武岩体及其层间错动带的渗透性分布特征,并提出了裂隙岩体渗透性随埋深分布的半经验公式[7],但其只考虑了岩体受自重应力作用的情况。周创兵等[8]开展了地应力对裂隙岩体渗透特性影响的理论研究,提出了岩体渗透系数与埋深之间呈负指数关系。
尽管已有许多学者针对裂隙岩体渗透性分布开展了相应的研究,但多局限于某一特定工程,关于不同因素对岩体渗透性的影响尚未形成统一的认识。本文通过系统分析多个水电工程岸坡岩体的钻孔压水试验资料,研究并总结峡谷区岸坡岩体渗透特性分布的一般规律。
2 岩体的透水性及其表征
岩体的透水性是指岩体允许透过流体的能力,若断裂、裂隙等呈密集状发育,且张开度较大,就会形成集中渗流带;相反如果裂隙被泥质紧密充填,或呈闭合状态,张开度减小,则其透水性就小。
在水电工程地质勘查中,常采用钻孔压水试验来测定岩体的透水性:在钻孔结束后,用栓塞或封隔器将钻孔按某一指定长度隔开,用不同的压力向各钻孔段压水,测定其相应的流量值,同时在隔开的试验段测定压力,并由此得到表征岩体透水性的参数—透水率q 和渗透系数k,它们描述了岩体介质的一种平均性质。《GB50287-2006 水力发电工程地质勘查规范》一般将岩体的透水性分为六级,见表1[9]。

表1 岩体透水性分级
根据压水试验得到的各试段流量随压力的变化关系可以确定岩体的透水率。透水率的单位为吕荣(Lu),定义为在1 MPa压力下,单位时间内(总历时10 min 左右)每米试段的平均压入流量,以L/(m·min)计。透水率在实际计算中通常采用最大压力阶段的压力值(Pmax)和流量值(Qmax),因为该组数据最接近吕荣值的定义压力,具体可由下式得到[10]:

式中:q 为试验段的透水率,Lu;L 为试验段长度,m;Qmax为最大压力时段压水流量,L/min;Pmax为最大试验压力,MPa。
渗透系数又称水力传导系数,定义为单位水力梯度下的流速。计算渗透系数通常采用巴布什金经验公式,将压水试验得到的透水率Lu 值转换成压水段岩体综合渗透系数k[10]:
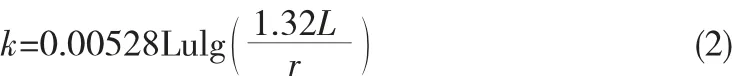
式中:k 为岩体渗透系数,m/d;Lu 为压水试验的吕荣值,L/(m·min);L 为压水试验段长度,m;r 为钻孔半径,m。
此外,Louis 等[1~8]依据现场钻孔压水试验建立了裂隙岩体的渗透系数与地应力之间的经验公式:

式中:k0为裂隙岩体的初始渗透系数;σ 为裂隙岩体所受的法向应力;α 为相应的衰减系数。
3 峡谷区岸坡岩体渗透性分布特征
3.1 埋深对岩体渗透性分布的影响
为了研究峡谷区岸坡岩体渗透性随地应力和埋深变化的分布规律,将位于金沙江的1#水电站左岸岸坡内埋深200 m内的所有440 段压水实验数据 (去掉极大值和不起压段的数据),一方面按照钻孔段的埋深绘制渗透系数分布散点图,见图1(a);另一方面,按照埋深每10 m 进行分段处理并计算相应的均值和中值,绘制渗透系数中值和均值随埋深分布曲线,得到图1(b)。

图1 1#水电站左岸岩体渗透性随埋深变化关系图
从图1(a)中可以看出,对于埋深小于80 m 的岩体,以弱透水性为主,占78.9%;微透水性和中等以上透水性(q≥10 Lu)岩体分别占11.4%和9.6%。对于埋深80 m~160 m 的岩体,则以弱偏下透水性(q=1~3 Lu)和微透水性(q<1 Lu)为主,分别占50.1%和31.3%;弱偏上透水段(q=1~3 Lu)岩体占16.2%,中等以上透水性仅占2.53%。对于埋深大于160 m 的岩体,则全部为弱偏下透水和微透水岩体。
在图 1(b)中,在埋深 60 m~80 m 和 120 m~160 m 两段透水率均值皆大于中值,这是因为在左岸这两段埋深中,局部存在强烈松弛~中等松弛型的深部裂缝,岩体裂隙较发育,再加上钻孔的分布较为不均,导致最终得到的中值偏小,从侧面也反映出岩体构造对渗透性的影响。
从不同埋深的统计成果看,一方面随着埋深的增加,地应力不断增大,裂隙的张开度随埋深逐渐减小,岩体渗透水性变小的趋势明显;另一方面由于钻孔在同一埋深不同的位置揭露的裂隙发育程度不同,导致其具有不同的渗透性,反映了裂隙岩体渗透的非均质性。
为进一步定量分析岩体渗透性随埋深和地应力的变化,首先对各个工程典型剖面上每个钻孔段所穿岸坡岩体的埋深信息按式(1)进行整理,再将透水率吕荣值通过式(2)进行换算;其次,统计各剖面上对应的钻孔段数据,以5 m 为单位将孔深离散化为整数深度,同时将对应的渗透系数也进行离散化,并且对离散化后的渗透系数和相对应的埋深值进行拟合;最后得到两者之间的关系呈式(3)所示的负指数型,拟合结果列入表2 中。

表2 各工程典型剖面岸坡岩体渗透系数与埋深的拟合结果
利用统计学的方法对数据进行分析,拟合得到的曲线相关性均较大,基本满足分析要求。如表2 所示,无论岩性是否相同,无论埋深范围是大是小,均可得到岩体渗透性随埋深呈负指数衰减;此外,若埋深范围越小,拟合结果越能反映出受地应力等因素的影响,拟合结果的相关性也越强。如1#水电站左右两岸统计的埋深范围较小,最终得到渗透系数随埋深的拟合曲线相关性均在0.9 以上;1#水电站工程区具有典型的高山峡谷地貌,两岸岩体拟合得到的初始渗透系数和衰减系数均较大,一定程度上反映出峡谷区岸坡岩体透水性深受区域地应力影响。
3.2 地层岩性对岩体渗透性分布的影响
由表2 中的拟合结果得知,从整体上看,相同岩性的岩体拟合得到的的衰减系数基本相近,而不同岩性的岩体初始渗透系数和衰减系数差异较大,比如3#水电站拟合得到的岩体初始渗透系数和衰减系数,与同样位于金沙江上的1#水电站相比均相差1 个数量级以上;但相同岩性岩体的初始渗透系数仍存在较大不同,比如2#水电站左右两岸初始渗透系数分别为0.2085 m/d 和0.0141 m/d,相差将近15 倍,考虑到左右岸压水试验数据所涉及的埋深范围不同,两岸风化卸荷程度也有所不同,因而可能导致岩体裂隙密集程度、开度范围等存在较大差异,从而导致初始渗透系数的不同。
由于不同岩性岩体中渗透性分布规律存在一定的差异,针对具有典型岩性分层的3#水电站,以其砂板岩、大理岩和绿片岩为研究对象,分析地层岩性对其岸坡岩体渗透特性的影响。左岸共完成压水试验数据774 段,高程1580 m 以上为T2-3Z2(3~8)(大理岩)和 T2-3Z3(1~4)(砂板岩);右岸共完成压水试验 853 段,高程1650 m 至 1880 m 为 T2-3Z2(3~6)(大理岩),低高程处为 T2-3Z2(大理岩)和T2-3Z1(绿片岩)。相比较而言,岩体透水性总体上左岸较右岸偏大,q≥100 Lu 的压水段次多出现在 T2-3Z2(5~8)(大理岩)及 T2-3Z3(4)(砂板岩)中,高程相对较高。将岸坡岩体按岩性分区间划分见图2,不同岩性的岩体透水性存在一定的差异,即使同一类型的岩体其透水性也会存在明显不同。总体而言,T2-3Z1(绿片岩)可以视为隔水岩层(q<3 Lu),大理岩与砂板岩在岸坡为相对透水岩层,只是局部存在相对的阻水岩体,两者透水性相当。
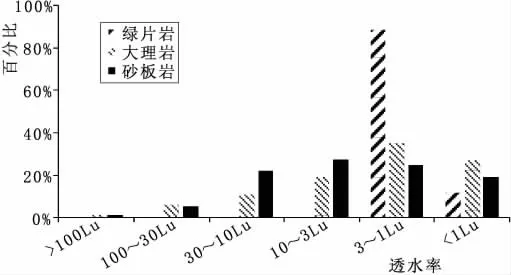
图2 绿片岩、大理岩与砂板岩不同透水性分段柱状图
3.3 风化卸荷作用对岩体渗透性分布的影响
风化卸荷程度不同会导致岩体渗透性分布产生差异,利用1#水电站岸坡岩体钻孔压水试验资料,选取钻孔分布较多、实验数据较为丰富的横Ⅲ、横Ⅲ’、和横Ⅳ剖面,将各剖面上每个钻孔段所钻穿岩体的风化卸荷信息进行整理;在对所得数据进行拟合分析的基础上,研究风化卸荷程度不同的岩体渗透性分布特征。各剖面无卸荷微新岩体(弱卸荷下限以下岩体)和风化卸荷岩体(弱卸荷下限以上岩体)统计结果见图3 和图4。

图3 1#水电站无卸荷微新岩体渗透性分布规律
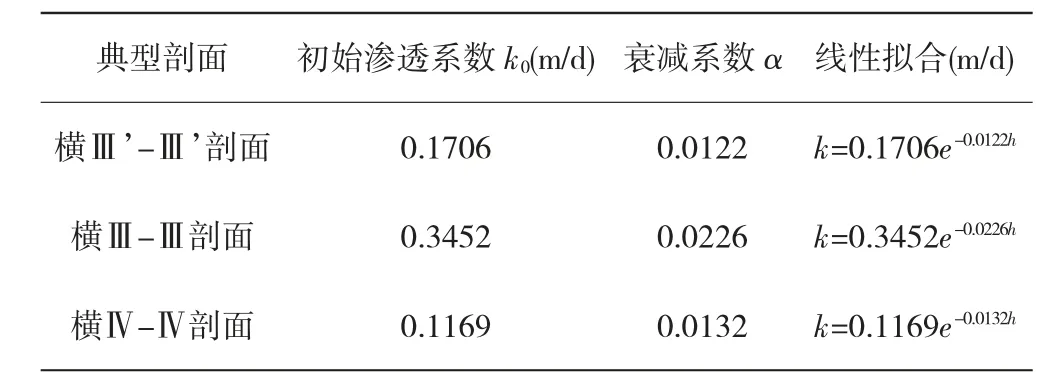
表3 1#水电站无卸荷微新岩体渗透系数与埋深的拟合结果
经过计算,根据线性拟合分析所得到的无卸荷微新岩体中渗透系数k 与深度h 的关系如表3 所示。由统计结果可知,在无卸荷微新岩体中,各剖面岩体初始渗透系数k0分别为0.1706 m/d、0.3452 m/d、0.1169 m/d,衰减系数 α 分别为 0.0122、0.0226、0.0132。由于微新岩体受风化卸荷作用较小,其岩体较为完整,渗透性较小,因而拟合得到的初始渗透系数与衰减系数也均较小。其中横Ⅲ剖面的渗透系数初始值和衰减系数均略大于其他剖面,从横Ⅲ剖面中各钻孔分布位置中可以看出,钻孔附近断层分布较为密集,且断层F1、F2 透水性较强,属强~中等透水,因而对该区域岩体渗透性影响较大,导致拟合得到的初始渗透系数与衰减系数偏大。

图4 1#水电站风化卸荷岩体渗透性分布规律

表4 1#水电站风化卸荷岩体渗透系数与埋深的拟合结果
经过计算,根据线性拟合分析所得到的风化卸荷岩体中渗透系数k 与深度h 的关系见表4。在风化卸荷岩体中,各剖面岩体初始渗透系数 k0分别为 0.7899 m/d、0.5926 m/d、0.3362 m/d,衰减系数 α 分别为 0.0366、0.0520、0.0826。
首先,对比以上两种不同风化卸荷程度岩体的统计结果后发现,风化卸荷岩体的初始渗透系数k0和衰减指数α 均大于无卸荷微新岩体。其次,从横Ⅲ、横Ⅲ’到横Ⅳ剖面,岩体初始渗透系数逐渐减小,这是由于各剖面中风化卸荷岩体裂隙发育程度有较大差异。①受地形影响,在右岸高高程Ⅲ’~Ⅲ线之间的突出山脊,卸荷更加强烈,深度更大。②在Ⅲ线~Ⅷ线之间,深部裂缝集中分布在水平埋深80 m~140 m 处,岩体破碎、松弛,工程地质性状差:其中在横Ⅲ’和横Ⅲ右岸高高程2850 m~2900 m和中高程2800 m~2843 m 均存在较为强烈的卸荷松弛,深部变形破裂普遍发育,松弛带厚度15 m~30 m,且根据断面裂隙统计资料,断面内裂隙也较为发育,对岩体的渗透性影响也较大;而在横Ⅳ两岸仅在低高程2733 m~2756 m 存在轻微松弛的深部变形破裂,岩体较为完整,破裂面张开度多小于1 cm,因而相比于横Ⅲ’和横Ⅲ剖面,横Ⅳ剖面的风化卸荷岩体初始渗透系数较小。
4 结论
本文通过系统分析多个水电工程的水文地质资料,揭示了壳状渗透结构对岩体渗透特性影响,并利用统计学的方法描述了岸坡岩体渗透特性随地应力、地层岩性和风化卸荷作用的变化特征:
(1)地应力和埋深因素:峡谷区岸坡岩体透水性深受区域地应力影响,渗透系数随着埋深的增加成负指数衰减,并且埋深范围越小,拟合结果越能反映出受地应力等因素的影响,拟合结果的相关性越强,越具有代表性。
(2)地层岩性因素:相同岩性的岩体拟合得到的的衰减系数基本相近,而不同岩性的岩体初始渗透系数和衰减系数差异较大,但相同岩性岩体的初始渗透系数也会存在较大不同(如2#水电站左右两岸初始渗透系数分别为0.2085 m/d 和0.0141 m/d)。
(3)风化卸荷因素:随着岸坡岩体风化卸荷程度的增加,渗透系数呈逐渐增大的趋势。
分析结果表明岩体初始渗透系数主要受裂隙初始张开度等的影响,而衰减系数则主要是受岩性和地应力条件的影响;风化卸荷岩体的初始渗透系数k0和衰减指数α 均大于无卸荷微新岩体;风化卸荷岩体的渗透性主要受风化和卸荷作用控制,渗透系数较大,微新岩体由于风化卸荷作用的减小,自重应力成为渗透性的主要控制因素,且渗透性较为微弱。

