基于拆解难度和模糊聚类的泛化报废汽车拆解成本预测

张春亮 陈 铭

上海交通大学机械与动力工程学院，上海，200240

0 引言

我国汽车产销量的不断攀升导致的报废汽车数量激增，使报废汽车回收利用产业面临巨大的拆解压力[1-2]。成本估计是项目或工艺实施初期衡量后续工作是否具有成本效益的重要手段，也是投资、竞标等活动的重要参考。成本估计往往是粗糙的，原因是初期缺少相关的数据或资料，无法或没必要进行精确的成本核算[3]。在市场竞争日趋激烈的背景下，如何快速地获取项目或工艺的动作成本对经营的投资或经营决策具有重要的意义[4]。面对当前汽车市场厂家多、型号杂的情况，迫切需要一种泛化的分类方法来快速评估拆解成本。

报废汽车拆解中，合理地规划拆解内容以获取更大的收益是市场行为的必然。近年来钢铁市场的低迷使汽车报废企业面临巨大的生存挑战，生产模式从以售卖废旧钢铁为主的传统再利用为目的的生产模式向以精细化、智能化为拆解手段，以再使用和再制造为目的的高附加值生产模式过渡。这种形势下，拆解企业对拆解内容必须有所取舍，报废汽车拆解成本的估计成为汽车报废行业考虑的首要问题，它直接关系到如何回收处理报废汽车，即拆解回收模式[5](手工拆解、拆解机拆解、拆解线拆解、直接破碎)的决策问题。国家政策、拆解技术、备件和材料的市场销售情况等虽会影响到拆解模式的选择，但选择性拆解始终是所有回收利用模式开展的前期工作，因为选择性拆解处置的是最能给企业带来盈利的高附加值零部件及危险或有环境影响的对象[6]。对于拆解企业而言，在车况等可能影响现场拆解的因素都不明确的情况下[7]，必须首先对报废汽车的零组件的拆解成本有一个快速估计，这样才能对比成本和市场行情来确定获利情况并最终决定哪些零部件需要被拆解。在这种不确定性的环境中，在拆解前准确预测拆解成本是不可能的或可能但十分耗时的。采用动态模糊聚类分析的方法[8]将拆解成本类似的零部件进行识别和归类，这样就可以根据聚类间的相似性，通过某些已知零部件的拆解成本快速推断出其他零部件的拆解成本，甚至是整车的拆解成本。由于本文所涉及的拆解实验是基于保护性拆解(拆解成本最高)的原则下获取的，因而假定所有被拆解的零部件均可再使用，但实际中来自报废汽车拆解零部件仅有一部分可再使用，这种情况有助于拆解企业获取更多的利润。

目前关于汽车拆解成本评价方面的文献十分有限。金晓红[9]通过拆卸时间评价了汽车螺纹连接零部件的易拆解性。传统的拆解成本统计分析方法是一种拆解后的成本精确计算方法，无法应用于拆解前的工艺决策评估，而在成本评估时建立精确的数学模型存在较大的难度[10]。本文在选择实验对象时以涵盖常见的乘用车车型为原则，并考虑实验数据的可获取性，以4台车况较好的大众品牌报废实验车型(2台轿车、1台运动型多用途汽车(SUV)、1台多用途汽车(MPV))的拆解数据为研究对象。由于实验对象是具有不同生产日期或不同结构配置的车型，在拆卸时所使用的拆卸工具、拆卸时间及拆卸难度等均会有所变化，故本文针对此种情况，在研究拆解难度影响因素的基础上，通过模糊聚类建立适用于3种车型的拆解成本评价模型，进一步探讨聚类模型的拆解成本误差评价方法并进行验证。

1 数据准备和分析流程

报废汽车拆解时除了受厂家、车型、年份、车况等不确定性因素影响外，还可能存在零部件增加或减少的情况[11]，为保证数据的完整性，本研究选取来自上海大众的报废实验用车(2台轿车、1台SUV、1台MPV)作为研究对象，拆解过程使用“手工+半自动化”的精细化完全拆解方式[12]，所有车型按同样的拆解次序进行拆解。为排除人员操作熟练程度对拆解时间的影响，整车拆解过程委托专业的拆解公司进行操作。表1所示为其中1台轿车的拆解次序和相关拆解数据。以发动机的拆解数据为例，在当前拆解次序下，共需拆解2个M10螺栓，拆解所需要的总时间为5 min，拆解后得到的发动机部件的质量为144.3 kg。分析中对近似数据进行了合并，如将二排、三排的后排座椅总称为后排座椅。为使模型简化并能应用于企业实际，本文在处理数据时未考虑螺纹类型、预紧力、材质和旋合长度等，而仅以螺纹直径来统一考量。

表1 报废实验轿车的拆解数据

报废汽车的拆解数据分析对拆解成本的评估与拆解工艺的决策是非常重要的，为此，需要规划数据分析和模型建立的流程。获得拆解数据后，首先应确定分析的指标，并在此基础上进行聚类分析，归纳出通用的聚类模型；然后进一步演绎出数学模型；最后分析误差并评估可行性。具体方法流程如图1所示。

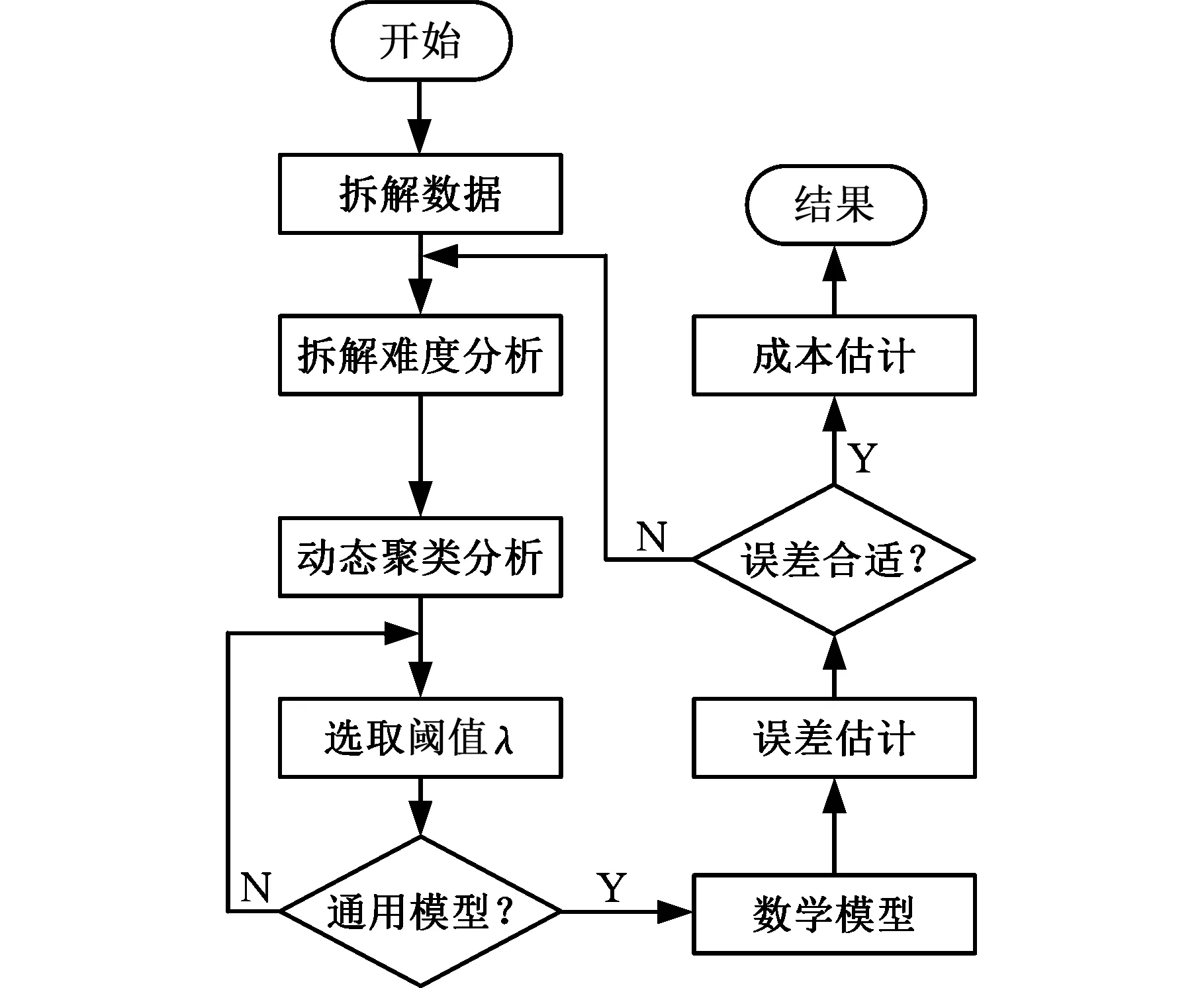
图1 拆解成本预测模型分析流程图Fig.1 Flow chart of disassembly cost prediction model

拆解成本预测模型分析流程具体如下：

(1)在拆解数据中，选取与拆解难度相关的数据作为原始数据矩阵的元素。

(2)将各车型被拆解零部件的拆解难度指标，根据相似性分别进行动态聚类分析。

(3)通过设定并分析阈值λ判断能否得到共性聚类，若是，则得到一个通用的聚类模型，否则，重新选取阈值λ进行分析。

(4)将聚类模型转化为数学模型，并求解相关系数。

(5)提出误差估计方法。

(6)根据误差分析结果判断误差是否符合需求，若是，则可以将对应模型用于成本估计，否则，重新考虑拆解难度指标并进行分析。

2 拆解难度的定义和分析

拆解难度可以理解为多种因素共同导致的拆解复杂性，其数学模型可以表示为

(1)

式中，d为拆解难度；x为拆解难度的影响因素；n为影响因素的个数。

螺纹连接是汽车零部件组装时的主要连接方式[13]。统计本文拆解实验数据发现，螺纹连接的拆解时间不一，其中55%的螺纹连接拆解时间均在[1，2)min范围内，如图2所示，这说明在对拆解难度进行分析时不能将拆解时间作为唯一的考虑因素。

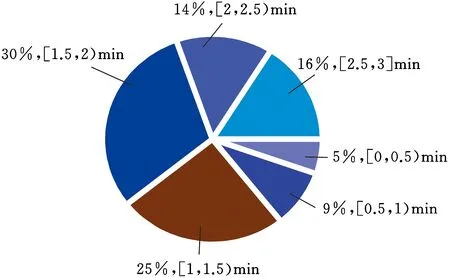
图2 螺纹连接的拆解时间分布Fig.2 The dismantling time distribution of threaded fasteners

广义上，影响拆解难度的因素包括拆解工具在空间上的可达性、在方位上的精确度要求、所施加力的强度、额外花费的时间和特殊情况等[14]。汽车零部件的装配中，螺纹连接和卡扣连接是常见的连接方式，由于本文重点关注用于再使用和再制造的零部件的非破坏性拆解，零部件尽可能以子装配的形式拆解，所以忽略焊接、铆接、过盈等需采用破坏性拆解的连接方式。冷凝器和发动机连接方式中包含卡扣，为方便对比，在此假定1个卡扣连接的拆解难度等同于2个M10螺栓的拆解难度。这样，本文所研究的内容就转化为螺纹连接的非破坏性拆解。在合理的拆解次序下，可达性、方位精度等对拆解难度的影响较小[14-16]，故重点考虑影响螺纹连接拆解的工具和工件方面的因素。从易于拆解统计的角度出发，本文将影响工件拆解难度的主要因素归纳为工件质量、拆解时间、螺纹直径和螺纹数量。由于研究的主要目的是对拆解前的成本进行预估，所以未考虑螺纹零件具体结构的影响。在各因素中，拆解所花费的时间在一定程度上体现了拆解成本，但工件质量、螺纹直径和螺纹数量与拆解时间具有相关性，所以4个因素中，拆解时间并不能作为拆解难度的首要考虑因素。根据拆解难度来进行成本预估是理想的拆解成本评价方式。

3 拆解难度的聚类模型

大部分报废汽车的零部件在拆解前很难了解它们的具体状况，因而拆解前对其易拆解性的评估是模糊的，故本文采用模糊聚类方法进行分析。

3.1 拆解难度的动态聚类分析

本文采用模糊动态聚类法对拆解难度进行聚类[17-18]。首先建立拆解难度原始数据矩阵，然后分别采用极差变换和最大最小法将数据矩阵标准化和标定，以建立模糊相似矩阵，最后使用传递闭包法获取拆解难度的动态聚类图。具体过程如下：

(1)原始数据矩阵的标准化和标定。在报废汽车拆解性的评价指标中，各指标大多具有不同的量纲，为方便比较，将所有指标值转化为[0, 1]间的量纲一值。本文采用极差变换的方法来消除量纲的影响，极差变换公式为

(2)

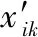
标定的过程就是获得各零部件基于各拆解难度指标的模糊相似关系，并建立模糊相似矩阵。本文采用最大最小法标定数据，表达式为

(3)

式中，xik、xjk分别表示表1数据的第i行和第k列和第j行k列所对应的拆解值；∧和∨分别表示取小和取大运算；rij为运算后得到的标定值。

本文所建立的原始数据矩阵和模糊相似矩阵的形式如下：

质量时间螺纹直径螺栓个数

(4)

(2)由于模糊相似矩阵不一定具有传递性，为实现模糊等价矩阵的转移，在此采用传递闭包法获取模糊等价矩阵。传递过程为：R→R(2)→…→R(2n)→R(2(n+1))。若R(2n)=R(2(n+1))，则R(2n)即为所求的传递闭包或模糊等价矩阵。

(3)将模糊等价矩阵基于不同的阈值λ进行布尔矩阵转换可以得到不同的聚类。拆解难度的动态聚类结果见图3(表1数据对应图3d)。

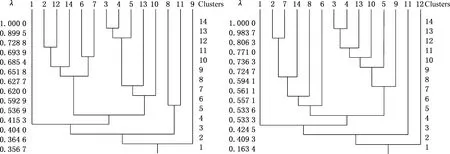
(a)实验车辆1 (b)实验车辆2

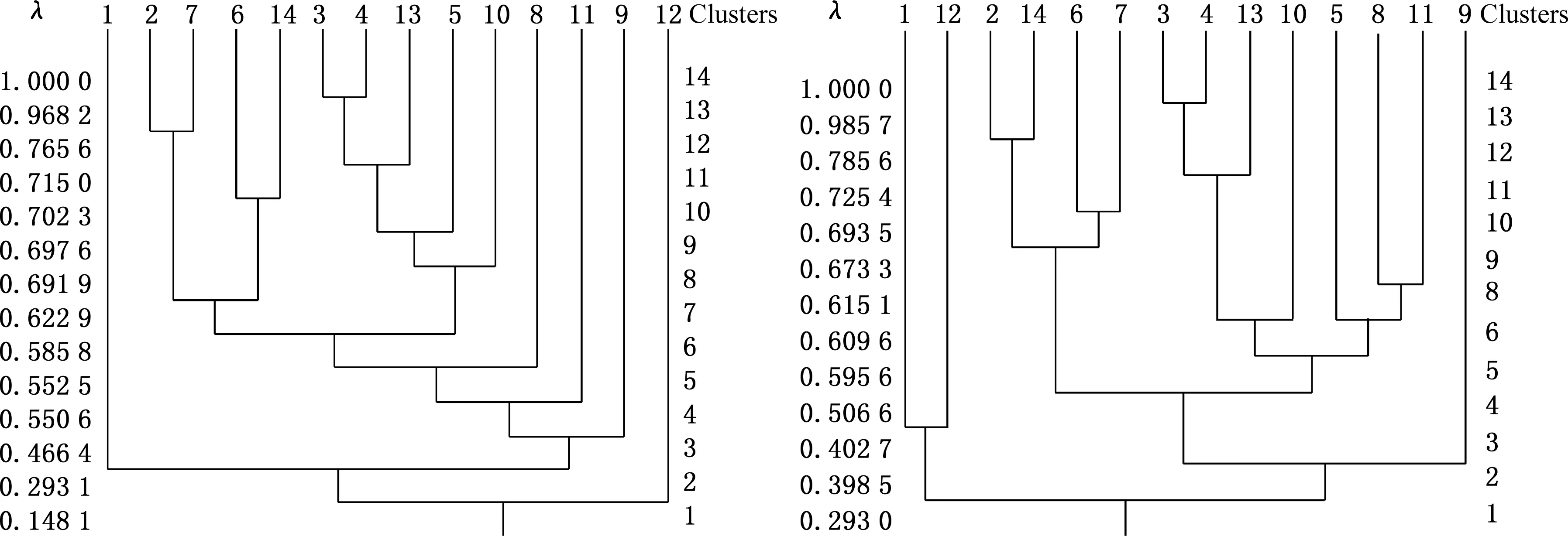
(c)实验车辆3 (d)实验车辆4图3 拆解难度的动态聚类图Fig.3 The dynamic clustering of disassembly difficulties

由图3可以看出，对于文中所进行的3种车型4组拆解实验，当聚类阈值λ取值为0.54～0.61时，所有拆解实验的聚类结果均可划分为5～6类(表2)，其中共性聚类为{1}、{2,6,7,14}、{3,4,10,13}，由此可以得到乘用车的一般聚类结果为{1}、{2,6,7,14}、{3,4,10,13}、{5}、{8}、{9}、{11}、{12}。在评估难度上，对于单车型，聚类数由6类增加到了8类，但对于所有车型，8种聚类为共性聚类，大大降低了评估的难度。通过聚类分析，将组成车型的14组拆解对象中的8组进行了归类，分析难度降低了36%，大大提高了评估的效率。

3.2 拆解难度指标权重值的确定

对不同的指标赋予不同的权重更加符合实际情况[19]。由表2可知：由于各车型的通用聚类中产生了新的聚类(由5～6类增加到8类)，同时需考虑4台车数据的差异性，故在新聚类中考察拆解难度的权重非常困难。为降低难度，取图3d进行分析，认为聚类{2，6，7，14}中的元素所对应的拆解难度值近似相等，根据表1数据建立超定线性方程组：

表2 拆解实验的聚类结果

13.9x1+20x2+30x3+16x4=
46.5x1+20x2+30x3+10x4=
21.7x1+45x2+25x3+24x4=
16.7x1+15x2+25x3+27x4

(5)

可以得到质量、拆卸时间、螺纹直径和螺栓个数4项拆解难度指标所对应的权重值xi(i=1,2,3,4),分别为1、0.38、7.79、5.43，由此可以得到6个聚类的平均拆解难度值(表3)。4种拆解难度指标按困难程度从高到低的排序依次是螺纹直径、螺栓个数、质量、拆解时间。被拆解零组件中，组合尾灯的拆解难度最低，而发动机的拆解难度较高，前灯总成、后座椅、中控、前后保险杠的拆解难度最高。通用聚类中的元素可以使用类比的方法根据表3近似确定相应的拆解难度值。

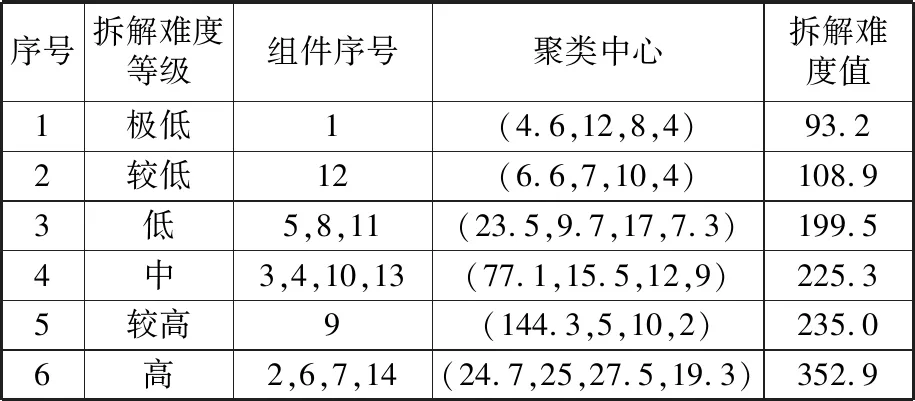
表3 不同聚类的拆解难度值

对于报废汽车中可能存在的被加装或分析中未包含的零部件，可以通过计算它们与聚类中心的聚合度来识别其所在的类别。该模式识别方法也可用于将新拆解的零部件划分到具体类别的问题。

4 泛化拆解成本模型及误差估计

4.1 报废汽车的泛化拆解成本模型

单个零部件的拆解成本Ci可以通过已知车辆拆解过程中发生的总成本CT和拆解难度d计算：

(6)

式中，di为单个零部件的拆解难度；k为零部件的个数。

(7)

4.2 报废汽车拆解成本的误差估计

拆解成本以拆解难度为研究对象，所涉及的参数包括质量、时间、螺纹规格和螺栓个数等。根据前面分析结果，可将报废汽车的零组件分为8个聚类，因此，总的拆解成本可表示为

C=C{1}+4Ca+4Cb+C{5}+C{8}+
C{9}+C{11}+C{12}

(8)

Ca=C{2,6,7,14}

Cb=C{3,4,10,13}

其中，括号内的数值代表聚类所涉及表1中的拆解零部件；Ca表示零组件2、6、7、14中的任意一个的已知拆解成本值或参考值；Cb表示零组件3、4、10、13中任意一个已知的拆解成本值或参考值。

在误差评估时为计算方便，假定拆解成本与拆解时间成正比。在此选取前3台车型的拆解时间数据的算术平均值作为Ca和Cb的值，使用第4台车型的数据进行验证。

车辆拆解成本的相对误差

(9)

式中，t为拆解时间。

通过计算可得前3台车型的拆解成本误差分别为28%、2%和19%。第4台车型的拆解成本误差为16%，在误差范围(2%～28%)内，从而验证了聚类方法的可行性。本实验车型涉及轿车、MPV和SUV三种车型，范围较广，若缩小车型范围将有助于进一步减小拆解成本的相对误差值。

5 结论

(1)针对报废汽车拆解行业对快速评估拆解成本的需求，建立了一种基于模糊聚类方法的泛化评价模型，将整车零部件聚为8类，降低了分析过程的难度。模型的贡献在于以分类的形式快速预测汽车组成零部件的拆解成本。拆解企业工艺人员根据车况选择可拆解的零部件后，可使用该模型快速评估拆解成本，因而也适用于不同车况下部份拆解方式的拆解成本评价，可提高拆解成本的预测效率。

(2)将普通轿车、运动型多用途汽车(SUV)、多用途汽车(MPV)三种车型作为分析研究对象，面向范围较广，模型的适用性广。分析过程淡化了车型间的差异性，创新性地使用权重来考虑拆解难度的影响因素，归纳了不同车型基于拆解难度的共性聚类特征，更加准确地评价了拆解成本。

(3)提出了模糊聚类模型的误差分析评价方法。通过聚类中的多数元素建立误差评价分析数学模型，然后将聚类中的其他元素代入模型进行验证，结果表明聚类中所有元素的拆解成本误差值均在范围(2%～28%)内，满足拆解前的成本估计需求，可以用于拆解前的工艺决策等过程。