超密集网络中宏微协作的干扰最小化资源分配
郑创明,刘龙伟,张海林,李勇朝
(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
为了满足第五代移动通信系统增加1 000倍数据速率[1]的要求,在现有网络架构的基础上,部署超密集的小基站增加频谱复用次数是提高频谱效率的一种有效方法[2]。然而,在一个网络中部署更多的小基站必然会带来严重的小区间干扰[3-4],从而限制着超密集网络频谱效率的提升。部分频率复用技术[5-6](Fractional Frequency Reuse, FFR)是一种易于实现且可靠性高的小区间干扰抑制技术。文献[6]提出采用FFR抑制异构网络的宏微之间的干扰,来提升超密集网络的频谱利用率。超密集网络中资源分配已经被证明是抑制小区间干扰和提升网络性能的另一种有效的技术[7]。其中静态博弈利用经典的纳什均衡预测移动用户的行为,利用静态博弈模型优化超密集网络的资源分配已经成为学术界研究的热点。文献[8]提出一种在超密集网络中采用双层博弈对Femtocell进行资源分配,并论证了算法的收敛性。文献[9]在分布式资源博弈的基础上,当可用资源分配不足时,采用分配减半策略和概率放弃策略来提高资源的利用率。博弈的资源分配技术采用搜索或迭代算法[8-9]能够达到性能最优,但由于极大的计算复杂度,这些方案不能直接运用于现有超密集网络的资源分配中。
文中综合分析和运用超密集网络中干扰抑制的各种成果,回避搜索和迭代算法,把超密集网络中的资源分配、小区间干扰协调和能效优化相结合,提出一种超密集网络中宏微协作的干扰最小化资源分配算法(Cross-tier Cooperation Resource Allocation for Interference Minimization, CCRA-IM)。首先,采用文献[6]中的FFR技术进行宏宏之间和宏微之间干扰协调;其次,运用宏微协作的干扰信息交互技术优化微小区的资源分配,把每个小区子带干扰信息量化为3个等级,这些信息被运用到资源分配过程中抑制超密集网络中的干扰;最后,对文献[4]中提出的动态负载自适应技术进行优化,当小区处于部分业务加载时,在保证用户服务质量不变的前提下,尽量把空闲的资源全部利用以降低潜在强干扰用户的发送功率,从而进一步降低了超密集网络中的干扰。
1 系统建模及优化目标
在超密集网络中采用文献[6]中提出的复用因子为3的FFR对宏小区之间和宏小区与微小区之间的干扰协调的技术框架,如图1所示。每个宏基站(Macro Base Station, MBS)包括3个宏小区,而每个小基站(sBS)只有1个微小区。用户根据接收到的参考信号接收功率(Reference Signal Receiving Power, RSRP)的大小确定自己的服务基站[10]。如果接收到宏基站的RSRP大于小基站的RSRP,则选择宏基站为服务基站。宏基站服务的用户表示为MUE,小基站服务的用户表示为mUE。
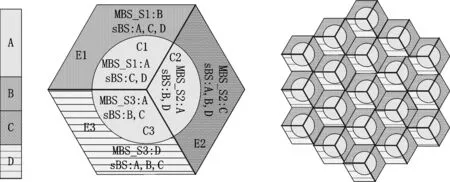
图1 采用频率复用技术的超密集网络系统频谱分割
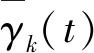
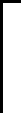
(1)
计算用户k需要分配物理资源块(Physical Resource Block,PRB) 个数Ck,其中,g为每个PRB承载的调制符号数。用户k分配的Ck个PRB对应的用于发送数据的资源单元(Resource Element, RE)集合用Πk表示,根据文献[12]目标解调门限γk(t)来计算,即
(2)
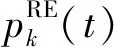
(3)
式(2)经过变化可得式(3)。通常情况下,在一次资源分配过程中假设干扰分布是保持不变的,且任意用户k在上行所分配的所有RE上发射的功率相同。因此,用户k在每个RE上发射功率与接收端的目标解调门限γk(t)成正比,目标解调门限越高,则需要的发射功率越大;目标解调门限越低,则需要的发射功率越小。
因此,用户k的上行发射功率可表示为
(4)

针对上述模型,文中优化的目标函数可以表示为一个带约束的优化问题:
(5a)
(5b)
其中,K为一次调度的用户数,Pmax为基站允许的用户最大的上行发射功率。
2 宏微协作的干扰最小化资源分配算法
式(5)所描述的优化问题是非确定多项式-难(Nondeterministic Polynomial-hard, NP-hard)问题[13]。采用穷举搜索的方式可以得到最优解,但需要计算N!次(N为超密集网络中用户数),这在现实网络中无法实现。受文献[4,6,8]的启发,文中采用一种次优的宏微协作的干扰最小化资源分配算法。
2.1 算法设计
宏微协作的干扰最小化资源分配算法,针对超密集网络中采用以宏基站覆盖的区域为基本单元进行干扰协调,主要包括宏微协作的干扰信息测量与传送和干扰最小化资源分配两部分。
2.1.1 宏微协作的干扰信息测量与传送
宏微协作的干扰信息测量与传送包括如下几个步骤:
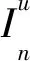
(6)
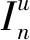
步骤2 根据QL量化每个子带的干扰,QL可表示为
(7)
步骤3 小基站向同覆盖的宏基站报告各个子带的干扰等级。
步骤4 小基站向同覆盖的宏基站请求与自己邻区子带干扰信息E,当邻区的个数为m且子带的个数为B时,E={e11,e12,…,e1B,…,em1,em2,…,emB},并把干扰信息E传送给调度模块。
2.1.2 干扰最小化资源分配
干扰最小化资源分配包括如下几个步骤:
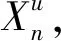
(8)
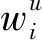
步骤2 基站采用PF调度算法的优先级计算公式[14],对M个待调度用户进行优先级计算,并按照优先级从高到低的顺序进行排列,优先级计算公式如下:
(9a)
(9b)
(9c)
其中,Qk(t)为用户k在时间t时刻的优先级,Rk(t)为用户k在时刻t的瞬时数据速率计算公式,W为信道带宽,β为滤波因子,Rk(t-1)为用户k在t-1时刻实际调度到的用户速率。
步骤3 标示本次调度中空闲的PRB,并统计空闲的PRB个数Ni。
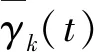
(10)
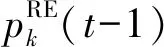

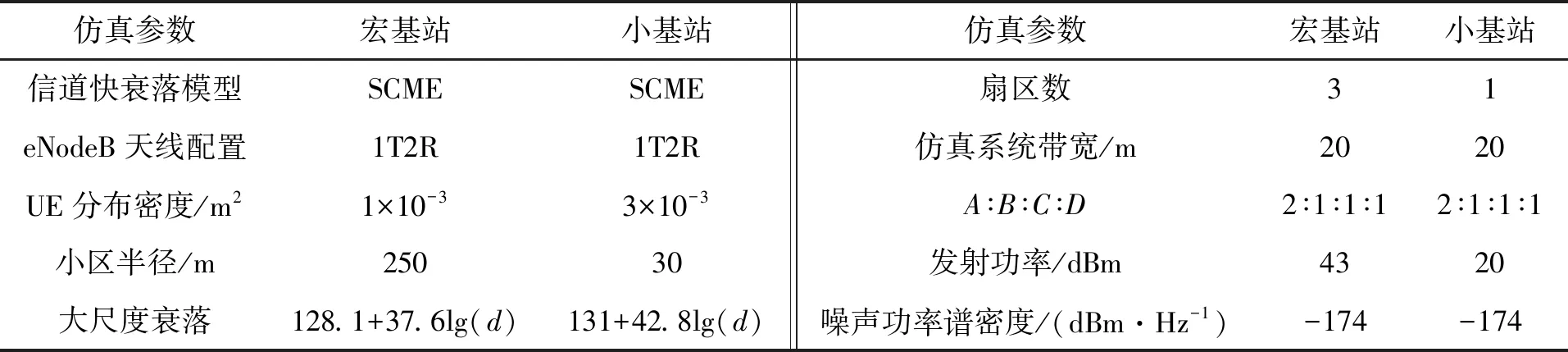
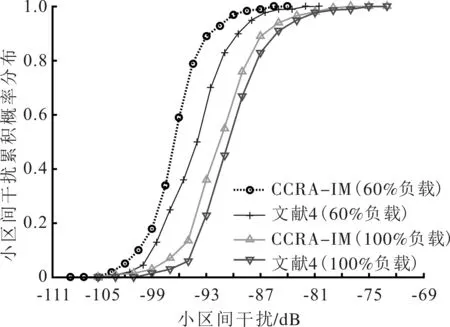
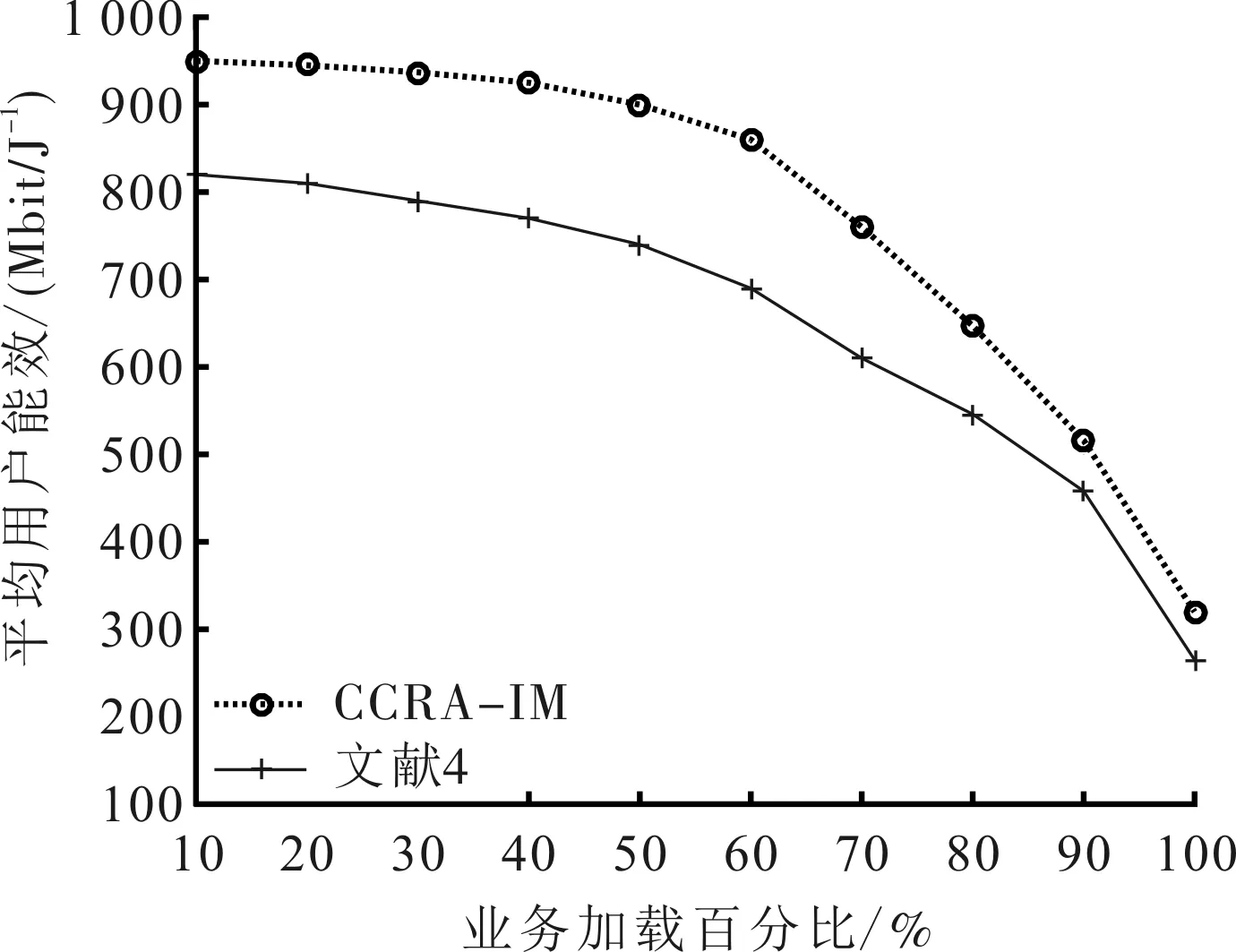
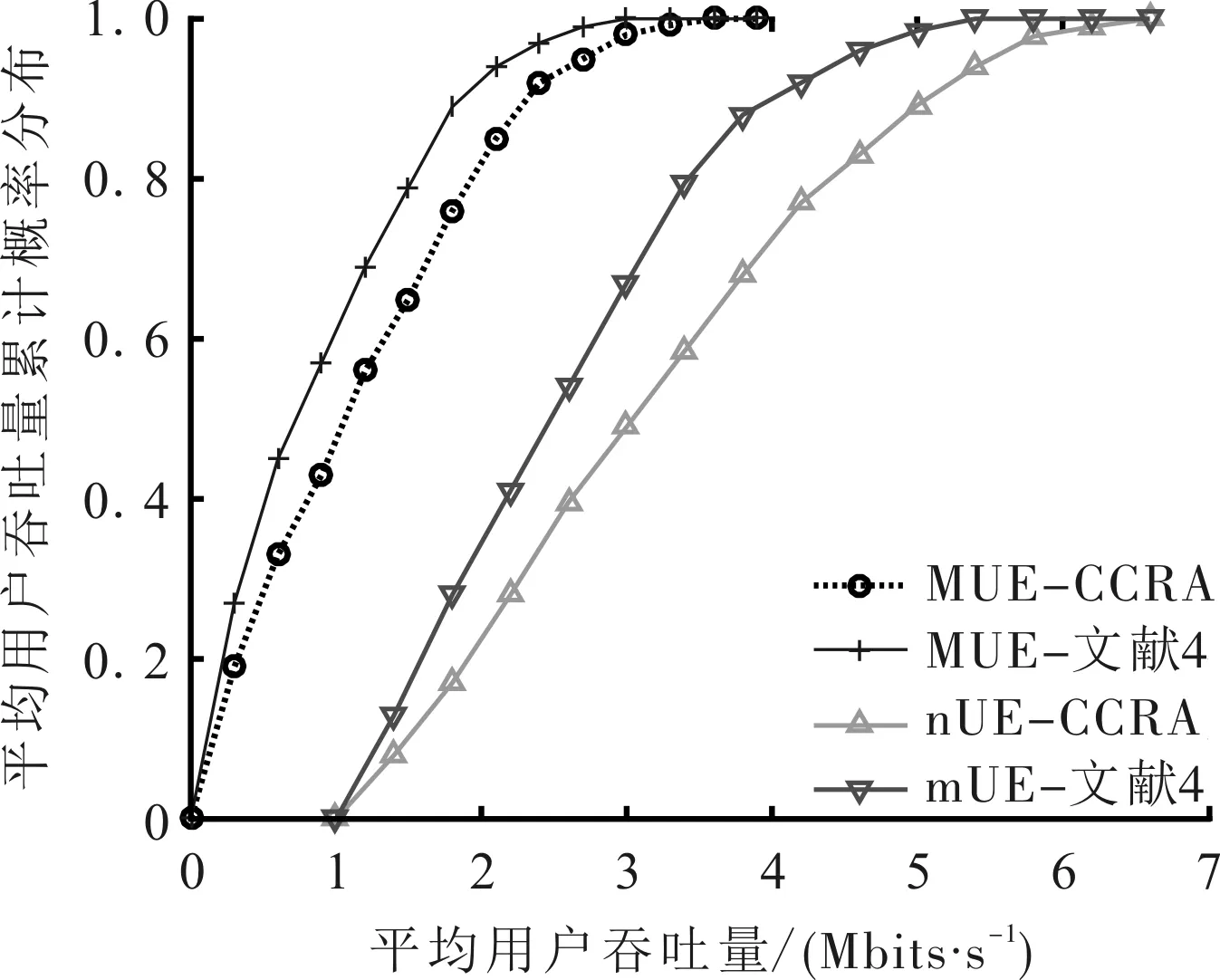
步骤7 如果Nt≥Ni,则执行步骤9;如果Nt 步骤8 选择单位RE功率最大的用户k,若MCS索引ωk≠1,则ωk=ωk-1,更新ζk、Ck、pk(t)和Nt,重复步骤6~步骤8;否则,选择单位RE功率第二大的用户v,采用与用户k相同的操作,以此类推;并记录本次调整的用户为L。 步骤9 如果Nt>Ni,则ωL=ωL+1,更新ζL、CL(t)、pL(t)和Nt。 文献[14]描述的比例公平调度算法是一个基本的资源分配算法,资源分配过程中没有迭代算法和搜索算法,其复杂度可表示为O(1)。宏微协作的干扰信息测量中主要的计算集中在步骤1和步骤4,步骤1由小基站完成,其计算复杂度可以看成资源调度的一部分,步骤4由宏基站完成,其复杂度等价于一次正常的资源调度,表示为O(1)。宏微之间的信息交互通过X2接口完成,不占用空口资源。干扰最小化资源分配中步骤1到步骤7属于资源预分配,其复杂度相当于一次正常的资源分配,表示为O(1);步骤8到步骤10属于资源分配调整,调整的用户数小于正常调度的用户数,计算复杂度小于O(1),表示为O(0,x)。因此,文中算法对宏基站增加的计算复杂度为O(1),小基站的计算复杂度为O(1,x),在技术可实现的范围内。 仿真参数如表1所示。仿真配置19个宏基站[13],在每个宏基站覆盖区域内随机部署30个小基站,宏基站覆盖的区域分成半径为200 m的中心区域和边缘区域。为保证仿真结果的精度,只收集中间7个宏基站覆盖范围内的用户数据。文中以超密集网络中动态的负载自适应部分频率复用技术[4]为对比算法,在干扰协调能力、能效比和吞吐量性能方面与CCRA-IM进行对比。对文献[4]中算法的仿真参数与CCRA-IM的相同。 表1 系统仿真主要参数 图2 小区间干扰分布CDF性能对比 图2为在超密集网络中采用CCRA-IM和文献[4]在网络业务量部分加载(60%业务加载)和完全加载两种场景中每个用户所测量的小区间干扰累计概率分布曲线。从图4可以看出,在小区间干扰协调能力方面,CCRA-IM两种场景中都表现出较好的性能。主要原因是CCRA-IM在部分业务加载场景中不仅充分利用了多余的带宽资源,降低了潜在高干扰用户的发射功率,而且给潜在高干扰用户分配无线资源时,CCRA-IM总是选择邻区子带干扰较小的无线资源,进一步降低了对邻区的干扰,因此干扰抑制能力强。在网络业务全加载场景下,CCRA-IM通过选择邻区子带干扰较小的无线资源给潜在的高干扰用户,降低了对邻区的干扰,达到了干扰最小化资源分配的目的。 图3给出了在网络加载的业务量从10%变化到100%的过程中,两种算法在能效性能方面的性能差异。仿真结果表明,CCRA-IM无论在网络业务部分加载场景还是在网络业务全部加载场景都表现出较好的性能,在网络业务部分加载场景中能效比提升高达15%,即使在网络业务全部加载的场景中,能效比提升约11%。这充分证明CCRA-IM能够适应于超密集网络中各个基站(宏基站和小基站)的无线资源分配策略。 图4是两种算法的平均用户吞吐量的性能对比。由于CCRA-IM在宏微之间采用干扰协调,使得系统内的干扰分布更加均匀,因此不论对MUE的吞吐量还是对mUE的吞吐量都有提升。从图4也可以看出,mUE的吞吐量大约是MUE的吞吐量的2倍,主要是由于小基站的带宽资源丰富,且服务的mUE数量较少。从图4可以看出,相对于文献[4]的算法,CCRA-IM无论对MUE的吞吐量,还是对mUE的吞吐量,性能提升均超过10%。 图3 加载不同业务量的能效比 图4 平均用户吞吐量对比 通过仿真证明,与文献[4]的算法相比,CCRA-IM在超密集网络中,在降低干扰强度、提升能效比和系统的吞吐量方面能够发挥较好的性能优势。 文中提出的CCRA-IM能够适应超密集网络中动态变化的业务场景,干扰抑制能力达1dB以上,能效比提升超过10%,用户的吞吐量提升超过10%,算法实现复杂度低。不足之处在于,基站之间需要交互干扰信息,必然会带来X2接口的信令开销。超密集网络的无线资源管理的研究任重而道远,未来的研究,把资源分配算法和网络自适应频谱规划相结合,应该会是一种更加有效的干扰抑制方法。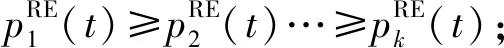
2.2 算法复杂度分析
3 算法性能仿真分析
4 结束语

