基于博弈论的保障性住房融资分析

■ 杨成（合肥高新技术产业开发区建设发展局）

一、保障性住房融资的利益相关方

在保障房融资建设的全过程中，无论是传统保障房融资模式还是新型融资模式，其主要利益参与方有5个，分别是政府部门，开发企业，保障房投融资平台，投资者和受保障人群。

（一）政府部门

政府是保障房项目的发起人，其目标是实现“社会福利的最大化”。政府通过政策手段和法律手段，对保障房市场进行调控，以促进我国住房保障制度的良性发展，解决人民的居住需求。

政府在保障房融资建设过程面临的最大矛盾是资金来源的矛盾，一方面，政府需要增加保障房建设和资金投入力度，出台激励政策措施鼓励开发企业进行保障房的融资开发，而另一方面，由于政府的非营利目标原则，保障房的开发往往以财政拨款为主。

（二）开发企业

开发企业是以利润为主导，进行房地产项目投资和开发的单位组织。其目标是实现“企业营利的最大化”。而保障房项目，由于其主要客户群体为中低收入阶层，相对于商品住房开发而言，保障房的开发利润率较低，因此开发企业对于保障房的融资开发热情不高。

在保障房融资建设的过程中，开发企业面临的最主要矛盾是利润，一方面，开发企业进行保障房的开发建设，需要大量资金投入，但由于保障房福利性质，其项目利润率较低。但另一方面，迫于政府政策导向，开发企业又不得不进行保障房的融资建设。因此，分析其融资建设过程本身，利润是开发企业矛盾的根源。

（三）保障房投融资平台

保障房投融资平台 是由信托公司、基金公司等发起成立的吸纳社会 闲散资本，用于政府保 障房融资建设的平 台机构。保障房投融资平台面临最主要的矛盾是产品风险控制与吸纳社会资本的矛盾。一方面，保障房投融资平台运营商希望赚取更大利润，从而提高保障房融资基金产品的资金回报率，以吸纳更多社会资本，另一方面，保障房投融资平台运营商考虑到保障房的系统性风险和较长的投资回收期，因而降低给予客户的资金回报率，从而达到控制风险的目的。在二者的动态均衡与博弈之中，保障房融资平台运营商最终找到二者的动态均衡点，即为平台产品的资金回报率。保障房投融资平台矛盾的核心是风险控制。

（四）社会投资者

社会投资者是指有充裕资金，渴望寻找渠道实现自身资产保值升值的潜在投资个人或组织，包括有闲散资金的个人、投资管理公司或私募基金机构等。其目标是实现自身资产的保值升值。

在保障房融资建设的过程中，由于政府财政拨款着实有限，社会投资者是参与保障房融资建设的一个重要资金来源。而社会投资者想要向保障房项目投资，却缺乏对应的投资机会，导致政府融资困难。社会投资者的核心在于融资渠道的缺乏。

（五）受保障人群

受保障人群是包括社会低保户，无收入群体和外来务工人员等一系列中低收入，缺乏住房保障的群体，是保障房融资建设流程的最终受益者。

在保障房融资建设的过程中，受保障人群只在最后保障房建成后分配时参与。其主要矛盾是个人需求与政府分配制度之间的矛盾。一方面，受保障人群希望政府早日分配住房，解决自身住房需求，另一方面，由于保障房一直处于供不应求状态，导致市场上既有保障房无法满足受保障人群的需求，例如某些地区中低收入阶层申请保障房需排队3-5年，这严重阻碍了我国住房保障制度的发展。

二、社会资本投资分析

（一）博弈论基本假设

博弈论，是研究决策主体发生相互利益关系时的决策最优化的均衡方法，其核心思想是博弈中的每一个理性决策主体必须在考虑其他决策主体的行为活动的基础上确定自身的最后决策策略。博弈分析一般由五个基本要素组成，即参与人、策略、次序、得失损益和均衡。

参与者（Player）：又称为局中人，即指博弈行为中独立参与决策，并承担相应结果的组织或个人。策略(Strategy)：又称为行动，指每个博弈主体在决策时可以选择的做法，行为或者经济活动发生的相应量值。次序（Sequence Order）：博弈行动的次序对博弈的影响非常重要，同样的博弈决策和参与人，行动次序不同，会导致每个参与人的最优选择也不同。得失损益（Payoff）：又称支付，是指博弈主体进行每一个博弈行动形成的表示得失的结果。均衡（Equilibrium）：指决策的所有参与者的行动策略最优化组合。

（二）社会资本和政府的博弈模型

假设政府进行保障性住房制度的完善需要付出成本B，如果社会资本进行投资进行投资，政府会获得收益W，如果社会资本不进行投资，则没有收益，同时如果社会资本进行投资而政府没有完善保障性住房制度，政府获得的收益为w（w＜W-B）；社会资本如果对于保障房进行投资，在保障房制度完善的情况下，社会资本的收益为θ1，在保障性住房制度不完善的情况下社会资本的收益有风险存在，假 设风险指数为P(0 ＜ P＜1)，则此时收益为θ1P，如果社会资本不进行保障性住房的投资转而投资其他商品，那么获得的收益在风险因素之后为θ（θ1P＜θ＜θ1）。则政府和社会资本之间的博弈分析如表1所示：

表1 社会资本与政府博弈分析

（1）（完善，投资）的收益是(-B+W,θ1)

在此种策略组合下，政府由于完善保障房的制度的付出是B，同时由于社会资本的投资获得W的收益，因此政府的收益为W-B；社会资本选择投资保障性住房，因为保障房的制度是完善的，因此社会资本的收益为θ1。

（2）（完善，不投资）的收益是(-B,θ)

此种策略组合下，政府由于完善保障房的制度的付出是B，同时由于社会资本没有投资保障房而没有收益，政府的收益为-B；社会资本没有选择投资保障性住房，将资金投向其他的商业项目，社会资本的收益为θ。

（3）（不完善，投资）的收益是(w,θ1P)

在此种策略组合下，政府由于社会资本的投资获得w的收益；社会资本选择投资保障性住房，因为保障房的制度是不完善的，投资具有一定的风险，因此社会资本的收益为θ1P。

（4）（不完善，不投资）的收益是(0,θ)

在此种策略组合下，政府的收益为0；社会资本将资金投向其他的项目，获得收益为θ。

（三）博弈模型的求解

通过上述分析，我们利用博弈论里面的划线法对于博弈模型进行求解，我们发现（完善，投资）和（不完善，不投资）都是该模型的纳什均衡解，没有唯一的纳什均衡解，因此这种方法舍弃。我们需要求取该模型的动态博弈均衡解。

我们假设政府完善保障房制度的概率为α，社会资本投资保障房的概率为β，如表1所示。利用概率对于政府和社会资本的收益期望进行求解。我们用E1代表政府的收益期望，E2代表社会资本的收益期望。

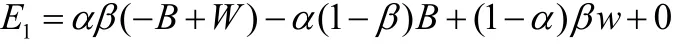
（1）政府的期望收益函数要达到最大值需要对其求导数，一阶导数为0时，函数值达到最大：

（2）社会资本的期望收益函数要达到最大值需要对其求导数，一阶导数为0时，函数值达到最大：

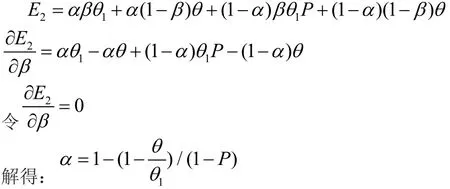
（四）博弈模型结果分析

着社会资本投资其他项目收益的增加而减小。这一点也很容易理解，当社会资本投资其他上项目的收益增加时，社会资本也就不会愿意投资保障性住房项目，政府完善制度的收益风险会增加，因此政府也就不愿完善保障房制度。

三、结果分析

通过分析我们可以知道，在保障性住房建设过程中，政府和社会资本是最重要的两个利益主体，而保障性住房的建设关键就是如何能够让社会资本愿意投资建设保障性住房，所以政府应当尽量完善保障性住房制度来促进社会资本进行投资。