双参数强度折减法研究中存在的问题分析

陈子玉，宋彦辉, 2，严 豪，陈康达

(1. 长安大学地质工程与测绘学院，陕西 西安 710054； 2. 西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054)

强度折减法自Zienkiewicz于1975年提出以来，在边坡稳定性分析中广泛应用[1]。相对于极限平衡法，强度折减法不需要事先假定边坡失稳滑动面，通过降低岩土体强度参数的方法，结合有限元方法，得到边坡失稳破坏时的应变和应力图。强度折减法研究大都基于库伦-摩尔强度准则进行强度折减计算[2-5]，在参数折减时对c，φ同步折减 (Strength Reduction Method,以下简称为SRM)。近年来有学者根据岩土体在变形破坏时强度参数c，φ的变化规律，采用双参数折减方式进行强度折减法研究[6-11](Double Reduction Method,以下简称为DRM)，在具体计算时，岩土体的c，φ值不同步折减。但是这些结果常常没有足够的理论支撑，同时众多研究的计算理念互不相通，强度参数c，φ数值的衰减规律和DRM中对c，φ的不同步折减不同步，使得DRM研究在“百花齐放”的同时，其结果互相矛盾。DRM是否合理，计算结果是否适合工程应用，尚没有充分的理论研究和实验验证。

相对SRM，DRM由于存在2个折减系数Rc，Rφ，其研究过程中需要确定双折减系数Rc，Rφ之间的关系，然后通过一定的数学运算求得综合稳定性系数F(Rc，Rφ)。DRM研究过程中面临的主要问题包括三个方面：(1)折减路径选择；(2)综合安全系数确定；(3)结果验证。这些问题给DRM的研究和应用带来了很多质疑和限制。强度折减法已经在国家规范[12]中得以应用，我国工程界开始正式将其纳入设计和工程治理中，关系到万千工程的安全稳定性，DRM作为一种新兴的边坡稳定性分析方法，受到越来越多的关注，因此有必要进行研究和探讨DRM应用的合理性。本文从分析强度参数c0，φ0的物理意义着手，就强度折减法本质进行讨论，同时逐一分析DRM存在的问题，以讨论和研究DRM应用的合理性和工程适用性。

1 DRM原理及强度折减本质讨论

1.1 强度折减本质讨论

有限元强度折减法对边坡稳定性系数的定义与简化毕肖普法相同[2]，两者都采用强度储备的概念计算边坡稳定性系数，通过对边坡岩土体强度参数折减迭代计算，边坡处于极限平衡状态时折减系数的大小等同于稳定性系数。通常在描述岩土体强度参数时有抗拉、抗压、抗剪等不同的强度参数，在边坡稳定性分析中，抗剪强度是主要控制因素。破裂面上，岩土体的抗剪强度值τf是一个关于σn，c0和φ0的函数：

τf=τ(c0,φ0,σn) (1)

传统有限元强度折减法在采用莫尔-库伦强度准则来表示抗剪强度大小时，对岩土体强度参数c0，φ0折减，莫尔-库伦强度理论公式如下：

τf=c0+σntanφ0(2)

式中：τf——莫尔库仑式确定的抗剪强度；

c0，φ0——岩土体黏聚力和内摩擦角；

σn——边坡滑动面上正应力。

从式(2)中可知，岩土体抗剪强度由黏聚力和摩擦强度组成。岩土体黏聚强度c0由静电引力、范德华力、颗粒间胶结、颗粒间接触点的化合价健、表观黏聚力等构成，摩擦强度σn·tanφ0由滑动摩擦和咬合摩擦构成。c0，φ0值是岩土体根据同一实验手段得到的，两者之间互相关联，但又不是简单的叠加，在不同实验手段中，如常规的三轴实验和直剪实验中，不同的应力水平和排水条件下测量出的结果不同，而且两者互相隐含，既有区别的一面，同样有相同的一面[13]。因此c0，φ0是计算岩土体抗剪强度的2个参数，且在物理实质上难以区分[14]。

此外，有限元强度折减法在计算过程边坡变形破坏的过程中，应力场不断变化[15]，即式(2)中的应力值σn在不断调整。而岩土体边坡中c0，φ0值受到边坡应力状态的影响，即不同的围压、轴向应力、不同的中间主应力[16]作用下，测得的c0，φ0数值不同。因此强度参数值随着应力场在不断调整。

因此对于一个确定的边坡稳定性问题，边坡内部应力场确定，其强度参数c0，φ0大小为定值，在计算时根据抗剪强度τf的折减进行计算，更符合强度折减法的本质。从式(2)中可以看出，SRM对式(2)左侧进行折减时，式(2)右侧正好对应了c0，tanφ0进行同步折减，这就表明SRM的本质是对抗剪强度进行折减，折减系数与强度储备系数相同，此时折减系数即为边坡的稳定性系数。而DRM计算中并没有对抗剪强度进行等比例折减，此时的折减系数与强度储备系数不同。

1.2 DRM原理

DRM通过岩土体初始强度参数c0，φ0采取不同的折减系数进行强度折减计算，具体计算如下：

(3)

(4)

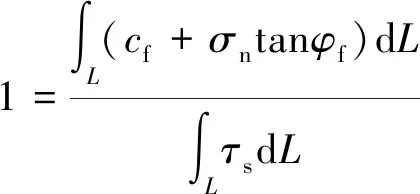
式中：τs——剪切应力；

L——边坡滑动面长度；

Rc，Rφ——c0，φ0的强度折减系数。

当Rc=Rφ时，DRM变化为SRM。式(5)为1时，表示边坡处于临界破坏状态，此时边坡的稳定性系数为1。

2 DRM存在的问题

2.1 折减路径选择问题

在DRM中，岩土体强度参数c0，φ0各自的折减系数Rc，Rφ之间的比例关系是需要首先确定的关键问题。通过折减比K=Rφ/Rc的选择，式(3)、(4)中双折减系数Rc，Rφ简化成1个，此时DRM折减路径的选择问题变成折减比K的确定问题。

朱彦鹏等[17]、康校森[18]、唐芬等[19]采用固定比例关系，根据强度参数在衰减过程中变化规律，使得K=Rφ/Rc保持常数不变，在具体计算时根据不同土体取不同的K值。文献[10]中根据c-tanφ临界状态曲线，采取统计学的方法得到固定的折减比K。薛海滨等[11]基于岩土体强度的弱化规律，根据简单的线性软化模型，采用非等比例关系，即Rc，Rφ之间呈一定的函数关系：

(6)

式中：cr，φr——岩土体残余阶段强度参数。

以上方法中对双折减系数的比例确定多基于浸水软化[6,18-19]、岩土体应变软化[11]或岩土体自然劣化规律[8]等，或采用统计学的方法[10]。岩土体抗剪强度参数的变化规律受到多种因素影响，这些研究成果受到样本值及不同岩土体之间差异性等影响，仅根据以上这些因素并不能准确得出c0，φ0的变化规律。式(6)采用岩土体应变软化模型得出的折减比例，是在边坡岩土体在稳定到极限平衡的过程中，岩土体强度参数由c0，φ0线性降低到cr，φr的假定上得出，但是有限元强度折减法的计算过程一般基于有限元计算不收敛得出，其计算终止时并不一定对应于强度参数值cr，φr，且岩土体的软化模型不局限于线性模型。因此以上对折减路径的选择不具有普遍适用性。

2.2 DRM计算原理

(1) 在有限元计算时，首先建立分析时步与场变量之间关系：

m=a+bt(7)

式中：m——场变量；

t——分析时步，且0≤t≤1；

a——场变量初始值，计算时一般设为1；

b——系数，根据边坡算例实际情况试算或经验取值。

(2) 将m与tanφ0设为反比例关系，即将DRM中内摩擦角φ0的折减系数Rφ作为场变量的值：

(8)

此时黏聚力c0与m之间关系如下：

(9)

(3) DRM计算时折减系数与场变量关系如下：

Rφ=m=a+bt(10)

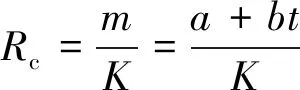
由上述可知，双折减系数Rc，Rφ均为场变量的函数。DRM计算时，通过场变量m的变化，实现了强度参数c0，φ0的折减，设置最小时步为△tmin，假设经过n步计算有限元计算收敛，此时场变量为mt，内摩擦角折减系数Rφ=mt，黏聚力折减系数Rc=mt/K。当K=1时，上述DRM计算过程和SRM计算过程相同。

对比SRM和DRM计算过程，结合式(10)和式(11)可知，在每一个时步计算时，DRM可以看成是以Kc0，tanφ0为初始强度参数进行SRM计算。为了进一步说明DRM与SRM之间的内在联系，研究DRM的本质，增加来自文献[19]中经典边坡算例如图1所示，算例中边坡坡高20 m，坡度45°，岩土体材料参数取值见表1。边坡计算时以有限元计算不收敛作为失稳判据，采用非相关流动法则，采用莫尔-库伦屈服准则，三角形网格单元，模型两侧及底面固定，模型顶部自由。

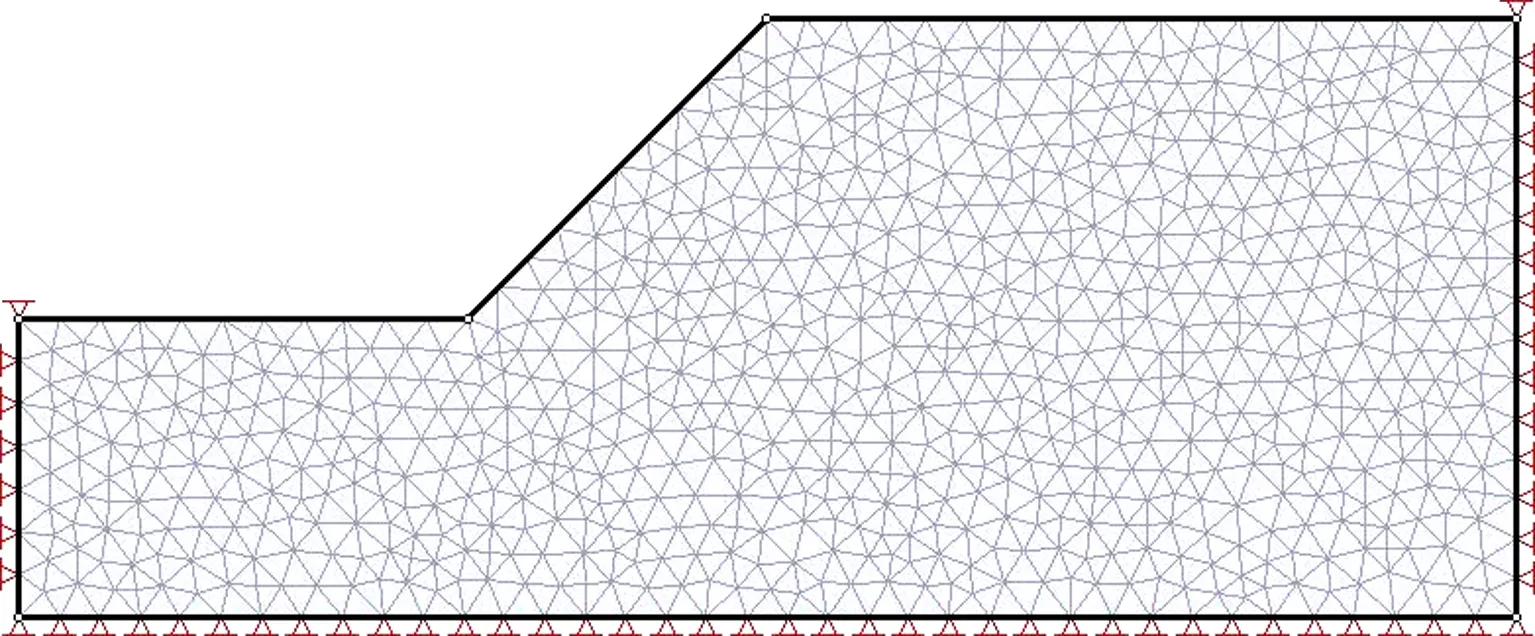
图1 算例有限元模型Fig.1 FEM model

γ/(kN·m-3)c/kPaφ/(°)μE/kPa2042170.3105

首先对算例边坡进行DRM计算，分别给定K值为0.2，0.6，1.0，1.2，1.6，2.0，2.2，2.6，3.0，共9组，计算结果如表2所示。然后针对不同K值，改变算例边坡中的强度参数，将黏聚力c0乘以K，内摩擦角φ0不变，以Kc0,φ0为初始状态参数进行SRM计算，K取值和DRM相同，分别为0.2，0.6，1.0，1.2，1.6，2.0，2.2，2.6，3.0共9组，SRM计算采用的初始状态参数和边坡破坏时临界状态参数及折减系数如表3所示。可以看出DRM计算出折减系数Rφ与SRM折减系数R完全相同，且其临界状态参数相同。因此DRM在折减计算启动时，可以看成是以(Kc0、tanφ0)为参数的SRM，即DRM的本质还是SRM。DRM相对SRM并没有计算原理上的改变，仅相当于改变了原始状态参数的SRM，依据文献[9]提出的参照边坡概念，将临界状态边坡作为参照边坡，待评价的边坡作为原始边坡，依据上述分析可知，DRM中参照的原始边坡出现了改变，使得双参数强度折减法对边坡的数值模拟出现了重大失真。

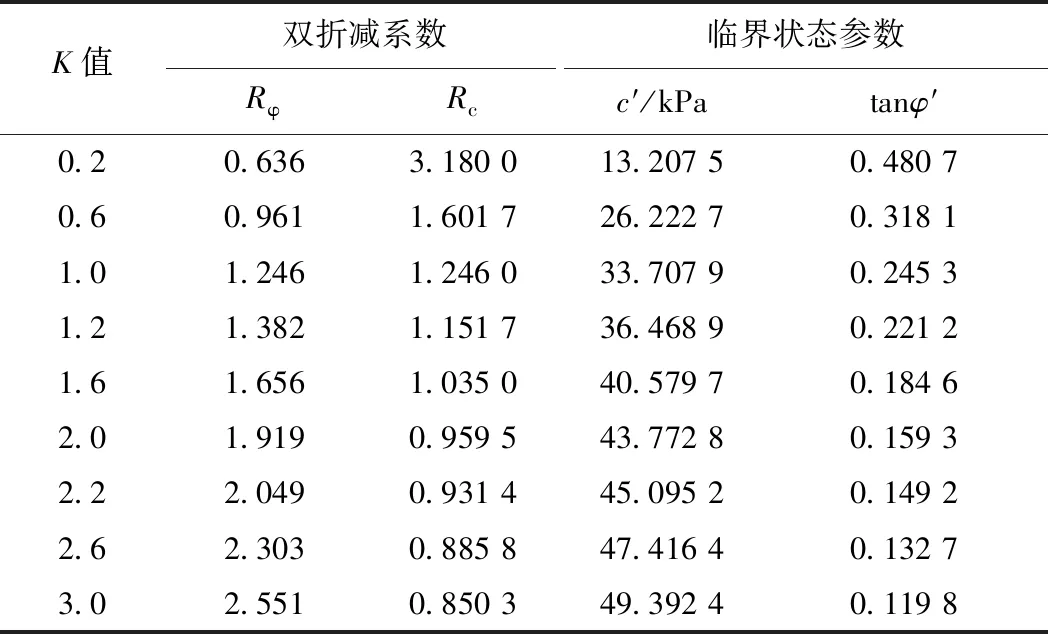
表2 不同K值下DRM计算结果Table 2 DRM results of various K

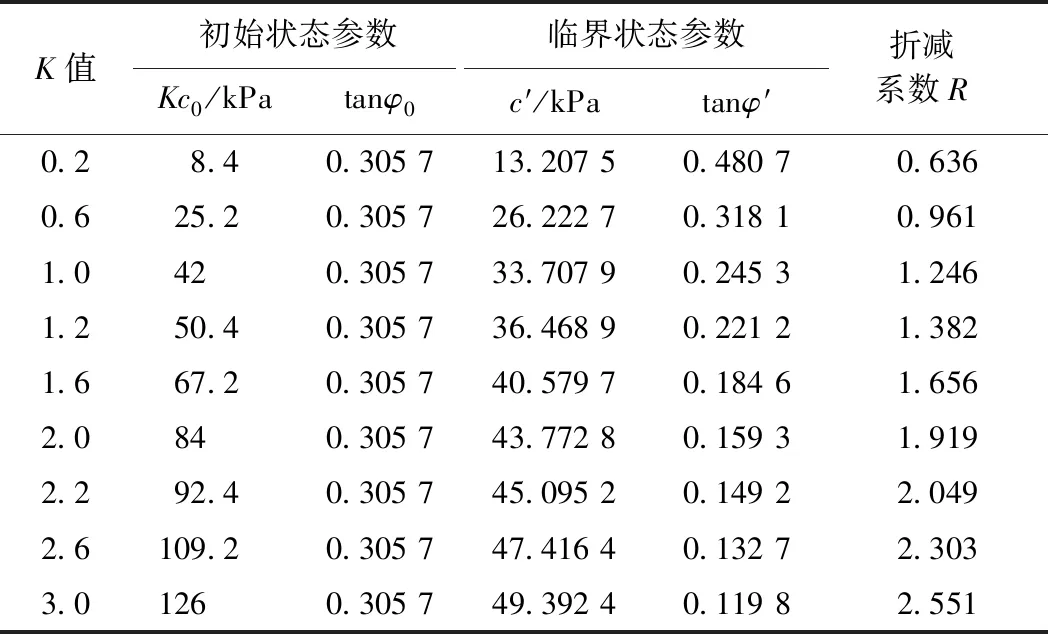
表3 不同初始状态参数下SRM计算结果Table 3 SRM results of various initial state parameters

2.3 DRM对边坡潜在滑动面的影响

取出边坡潜在滑动面上一个单元点(图2)，单元点应力按照主应力形式表示如下：

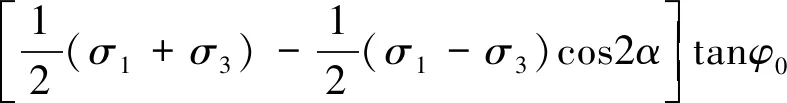
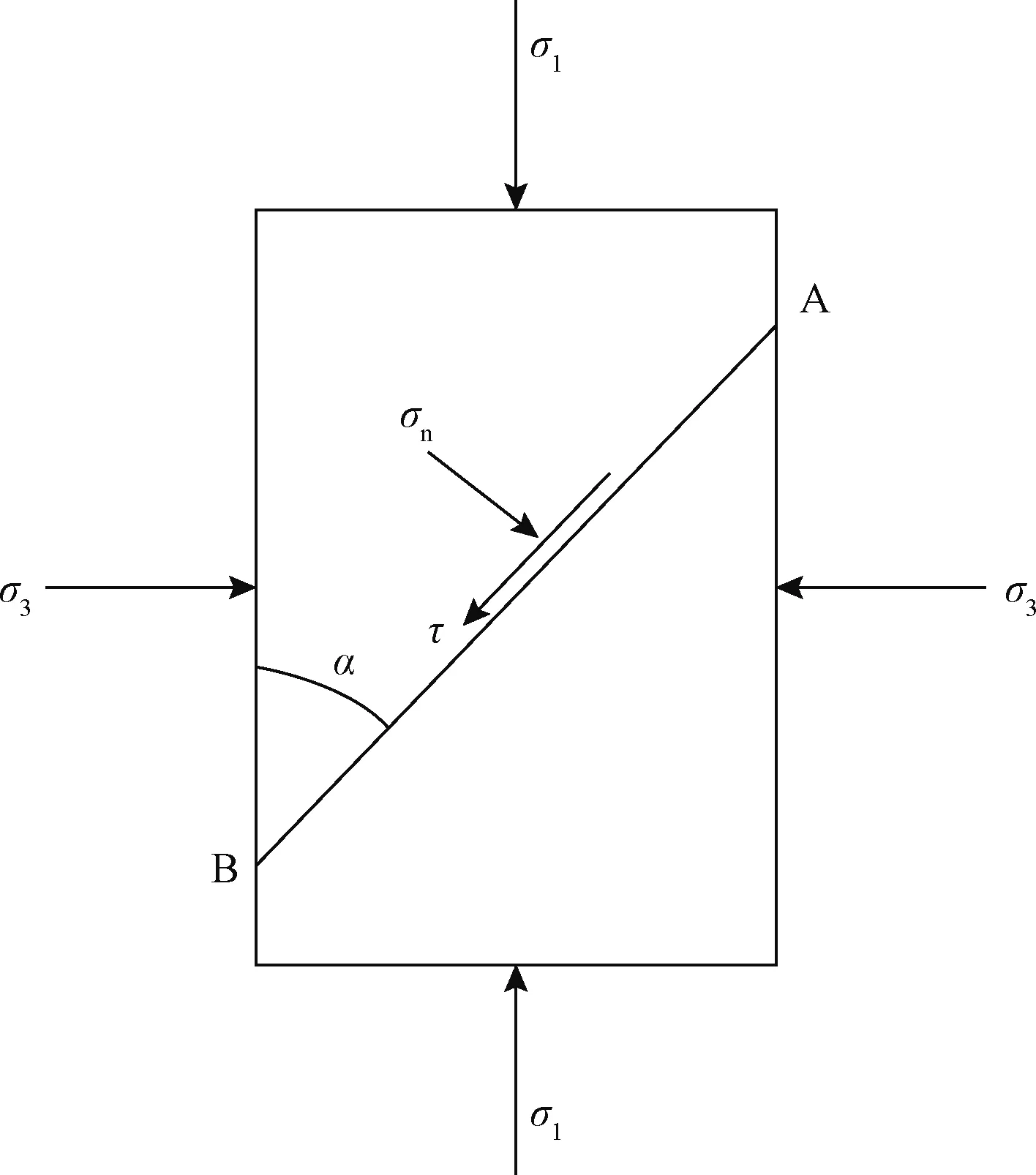
图2 单元受力情况Fig.2 Stress of unit

式中：σ1，σ3——破坏面上一点的最大主应力、最小主应力；

α——最危险滑动面AB与σ3之间的夹角。

由式(12)通过变换可以得到最危险滑移面角度α计算公式：

(13)

由式(12)与式(13)可以看出，对于一个确定的边坡，边坡岩土体强度参数c0，φ0已知，边坡内部应力场确定时，边坡潜在滑动面是确定不变的。对式(13)右侧的强度参数按照SRM进行等比例折减，得到式(14)，虽然式(14)右侧进行了参数折减，但是式(14)与式(13)计算结果相同。式(14)表明SRM在计算时，等比例折减强度参数c0，φ0并未改变边坡滑动面。

(14)

对式(13)右侧c0，φ0分别以Rc，Rφ进行折减，得到式(15)，可以看出式(13)与式(15)的结果明显不同，即DRM计算时边坡滑动面的形状发生了变化。

(15)

对前文中边坡算例采用DRM计算，在不同K值下，有限元计算临界状态最大剪应变带云图如图3所示。

图3 不同K值下临界状态最大剪应变云图Fig.3 Maximum shear strains of the critical state under different values of K

由图3可以看出，当K=0.2时，最大剪应变带靠近坡面，剪出口位于坡脚上方；K=1.0时对应于SRM计算结果；随着K值增大，K=2.0、K=3.0时最大剪应变带加深,最大剪应变带向坡内移动。因此DRM在计算时，随着K取值变化，边坡潜在滑动面出现变化，K值增大，滑动面加深，K值减小，滑动面靠近坡面，剪出口上移。

袁维等[20]指出DRM在计算时由于对c0，φ0的非等比例折减，其滑动面破坏形式和SRM不同，并以此作为DRM优于SRM的证据。对于一个稳定边坡，其稳定性系数大于1，其破坏虽然存在无数种可能，而根据潘家铮最大、最小值原理[21]，其破坏面会沿着抗滑力最小的滑动面发生，即边坡在物理力学参数和外部边界确定时，在不受外界影响时，其潜在破坏面唯一确定。而根据林杭[22]、王少华等[23]的研究，边坡岩土体强度参数c0，φ0的相对大小，控制着边坡剪切破坏面的形式：在一个外部边界固定的边坡中，内摩擦角φ0值减小，滑动面加深；黏聚力c0减小，临界滑动面靠近坡面。综合以上分析，结合式(15)可知，DRM由于在折减计算时，由于折减比K的作用，改变了边坡的原始参数，从而导致了计算出的滑动面并非边坡潜在滑动面。

3 综合稳定性系数及结果验证

在工程实践中，一般采用固定的稳定性系数来评价边坡稳定性，SRM将有限元计算不收敛时的折减系数作为边坡的稳定性系数，而DRM在计算时强度折减系数有两个，对一个确定的边坡，边坡稳定性系数应当如何确定？不同的研究者根据不同的研究方法提出了边坡稳定性系数的确定方法。

唐芬等[6]、陈依琳等[24]采用平均值确定综合稳定性系数F:

(16)

朱彦鹏等[17]、袁维[20]采用Rc，Rφ乘积开方确定综合稳定性系数F:

(17)

YUAN等[25]采用统计学的方法，通过利用大量不同形态特征的边坡数值算例，采用数据拟合的办法确定边坡的综合安全系数F：

(18)

朱彦鹏等[26]还提出了采用Rc，Rφ中最小值来确定综合稳定性系数F：

F=min(Rc，Rφ) (19)

Isakov等[27]、赵炼恒等[28]认为，综合稳定性系数F为Rc，Rφ两者的隐含表达式，通过c0，φ0的不同折减系数Rc，Rφ之间的函数关系式，利用双参数强度折减最短路径来定义综合稳定性系数F：

(20)

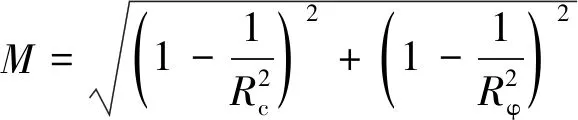
薛海滨等[11]、王强志等[29]将综合稳定性系数F定义为边坡土体强度参数折减前滑动面提供的抗滑力与极限状态下滑动面提供的抗滑力比值，从而根据黏聚力与摩擦强度的权重确定出综合稳定性系数。

但是上述研究方法在理论上差别较大，在对最终稳定性系数确定上理论依据不充分。如式(16)、式(17)在确定边坡综合稳定性系数时，其计算式并没有明确的物理意义，并且缺乏理论证明。式(19)由于采用最小值来作为边坡稳定性系数，忽略了另一个参数的强度贡献。式(18)、式(20)虽然有公式的推导，但是其稳定性系数F值的物理意义并不明确，而且基于数据拟合的公式推导，导致其适用性受到样本值的影响而难以推广。DRM认为黏聚力c0和摩擦系数tanφ0发挥作用不同，并因此采用不同的折减系数，但是在确定综合稳定性系数时，并没有体现出黏聚力c0和摩擦系数tanφ0发挥作用不同的影响，各种综合稳定性系数确定方法在原理和结果上不能统一。

另外，DRM在综合稳定性系数的确定方法上难以应用在多层岩土体边坡，已有文献资料对这一问题均没有提及。在实际工程实践中，纯粹的均质土边坡基本不存在，即使对于单一巨厚沉积层的边坡，也会由于地下水位、卸荷裂隙、风化等原因，呈现出分层性。在双参数强度折减法计算过程中，对于多层土或含裂隙、节理的岩质边坡，多层土之间的强度参数ci，φi各不相同，含节理、裂隙岩质边坡岩块和节理面强度参数不同。按照DRM理论，假设某边坡内有n层岩土类型，n种类的岩土体都会对应2n个折减系数，此时边坡的稳定性系数无法用式(16)～(21)所给定的方法确定出一个单一的综合稳定系数F。

SRM一般在计算机有限元软件中进行应力、应变分析，并根据三类判据的不同在一定精度范围内和极限平衡法做对比(一般取5%为界限)。这是由于极限平衡法已经在实际工程建设领域得到了检验，而5%的计算误差在工程允许的范围内。但在某些研究中，将DRM的综合稳定性系数与SRM计算结果进行对比，或者与其他研究者的不同综合稳定性系数确定方法之间作对比，其精度误差在2%以内[8]，虽然在一定程度上计算结果与极限平衡法和传统强度折减法一致，但是依前述分析可知，两者之间并无本质上的不同，偏离了边坡稳定性计算的本质。

4 讨论

DRM相比SRM固然可以反映岩土体强度参数c0，φ0的变化规律，但是在具体的研究和应用上偏离了强度折减的本质，存在着物理意义不明确、概念混淆的问题。在不同的数值分析软件中，SRM只需要确定出数值计算收敛、位移突变、塑性区贯通三种破坏判据中的某一种即可求得边坡的稳定性系数，目前已经在国内外的工程实践和理论研究中得到了大量应用，而DRM相较于SRM多了折减比K的确定、综合稳定性系数确定等两个步骤，此外由前文分析可知，DRM不适用于多层边坡的稳定性分析。SRM和DRM作为一种数值计算手段，相较于传统极限平衡法，可以对边坡内部应力及应变场进行分析无疑是一种进步，但是同样地由于建模及数值分析手段的限制，在具体计算时参数的输入及结果输出上引起了很多争论。在边坡稳定性分析的工程实践中，首要的是确定出边坡的稳定性系数和潜在滑动面，而DRM由于本身计算原理和特性，其计算结果受到折减比K的影响而呈现多样性，使得该方法更加复杂和难以推广，强度折减法(SRM)的研究应该更多地针对强度准则选用、输入参数的选取、破坏判据的选择及输出结果分析等内容。

5 结论

(1)双参数强度折减法与传统强度折减法无本质上不同，有限元计算时两者计算原理相同，但双参数强度折减法与基于强度储备的稳定性系数计算方法不符。

(2)折减比K的存在改变了边坡潜在滑动面的形态，不同的K值会得到不同的边坡临界滑动面，与边坡实际不符。

(3)已有的双参数强度折减法研究对多层岩土体边坡不适用，无法确定出多层岩土体边坡的稳定性系数。