基于Bezier曲线的数字图像加密研究

李晴晴，杭后俊，尹天乐

(1.安徽师范大学 计算机与信息学院，安徽 芜湖 241000；2.网络与信息安全安徽省重点实验室，安徽 芜湖 241000)

0 引 言

由于网络环境本身的复杂性和易变性，使得信息在网络中传输时的安全问题愈加突出[1]。据不完全统计，网络中传播的信息，大约有百分之七十是以数字图像形式体现出来的，因此数字图像加密技术就成了研究的热点问题。现在常用的图像加密算法中，基于现代密码体制的图像加密[2-3]、基于矩阵变换/像素置换的图像加密[4-5]、基于秘密分割与秘密共享的图像加密[6-7]等由于图像数据存在大量冗余，像素之间具有很强的相关性，图像具有特定的数据格式等特点，并不能完全满足图像加密的要求[8]。而混沌系统由于自身的特殊性质如对初始条件和参数高度敏感，随机性强，遍历性等使其非常适合图像加密[9-14]。现在很多基于混沌系统的图像加密算法以时间和空间换加密强度的思想，大多采用复杂的加密算法和变换流程来获取更高效的加密指标，这样自然导致加密解密速度慢、算法的复杂性高等缺陷，加密效率不如一维系统。

Bezier曲线是一种由控制点控制的多项式曲线，具有诸多优良性质，广泛应用于形状设计中。研究表明，单位区域内的二次曲线映射可以产生混沌序列[15-17]，而有理二次Bezier曲线可以精确表示二次圆锥曲线[18]。基于这一理论，文中提出了一种基于有理二次Bezier曲线的数字图像加密算法。根据有理二次Bezier曲线的内在特性，提出了一个一维有理映射函数，当内权因子在一定范围内取值时，该迭代函数具有混沌特性，产生混沌序列，进而构造加密因子与像素灰度进行运算并置换，最终得到加密图像。

1 有理二次Bezier曲线

根据CAGD理论[13]，有理二次Bezier曲线

p(u)=

(1)

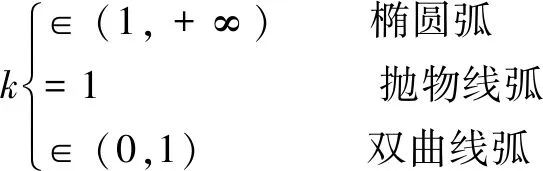
对于标准型，可用内权因子ω1进行分类：

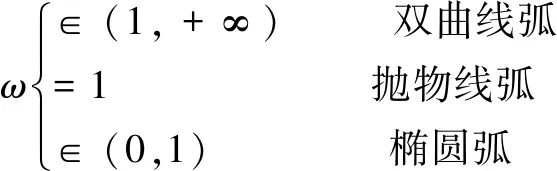
有理二次Bezier曲线具有如下重要特性：

(1)如果保持其余权因子、所有控制点不变，让ω1在某个范围内变化，就会得到一族曲线。再固定参数u，则这一族曲线上参数u相同的点位于一条直线上。

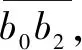
2 基于Bezier方法的图像加密算法

2.1 加密系统

据式1可知，由控制点b0=[0,0],b1=[0.5,(1+ω)/ω],b2=[1,0]确定的标准型有理二次Bezier曲线为：

(2)

显然，该曲线上点的x坐标取值范围为x∈[0,1]，而y最大值为曲线上肩点的y值，即ymax=y(0.5)=1，所以y坐标取值范围为y∈[0,1]。

∀x0∈(0,1),∀ω>0，根据内权因子对曲线形状的影响特性，构造如下一维有理映射函数：

(3)

李雅普诺夫指数(Lyapunov)是评判一个系统是否具有混沌性质的重要指标，Lyapunov>0说明该系统具有混沌特性。对任意一维映射xn+1=f(xn)，其李雅普诺夫指数的计算方式如下：

其中，x0为系统的初始值；x1,x2,…为每次的迭代值；n为迭代次数。

对于有理映射函数，其李雅普诺夫指数为：

λ=

(5)

经计算可得，内权因子ω至少在区间[0.7,1.5]上取值时λ大于零，即由式3产生的序列{xi}(i=0,1,2,…)具有混沌特性。图1为该混沌序列产生过程的示意图。

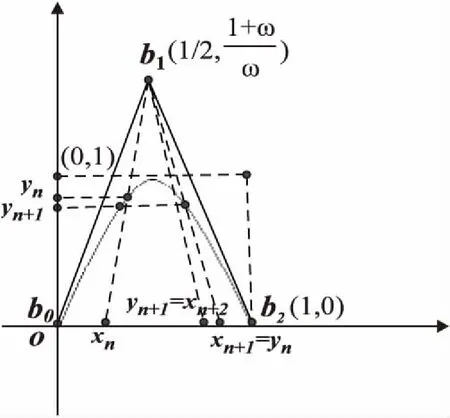
图1 序列{xi}(i=0,1,2,…)产生示意

2.2 加密算法

设明文图像I大小为m×n，I(i,j)(i=1,2,…,m,j=1,2,…,n)表示像素的灰度值。为了保证序列的混沌效果，可以预先对有理映射函数(3)迭代适当的次数N，比如N=100。依次读取图像I的每一像素I(i,j)，将有理映射函数(式3)迭代8次所产生的实数序列在其最大值和最小值之间的每个数与其平均值avg进行比较，若大于avg则对应位置1，否则置0，得到一个8位二进制序列，称之为加密因子。再将该加密因子与当前像素灰度值进行异或运算，并用运算的结果替代当前像素的灰度值，从而得到密文图像。具体算法步骤如下：

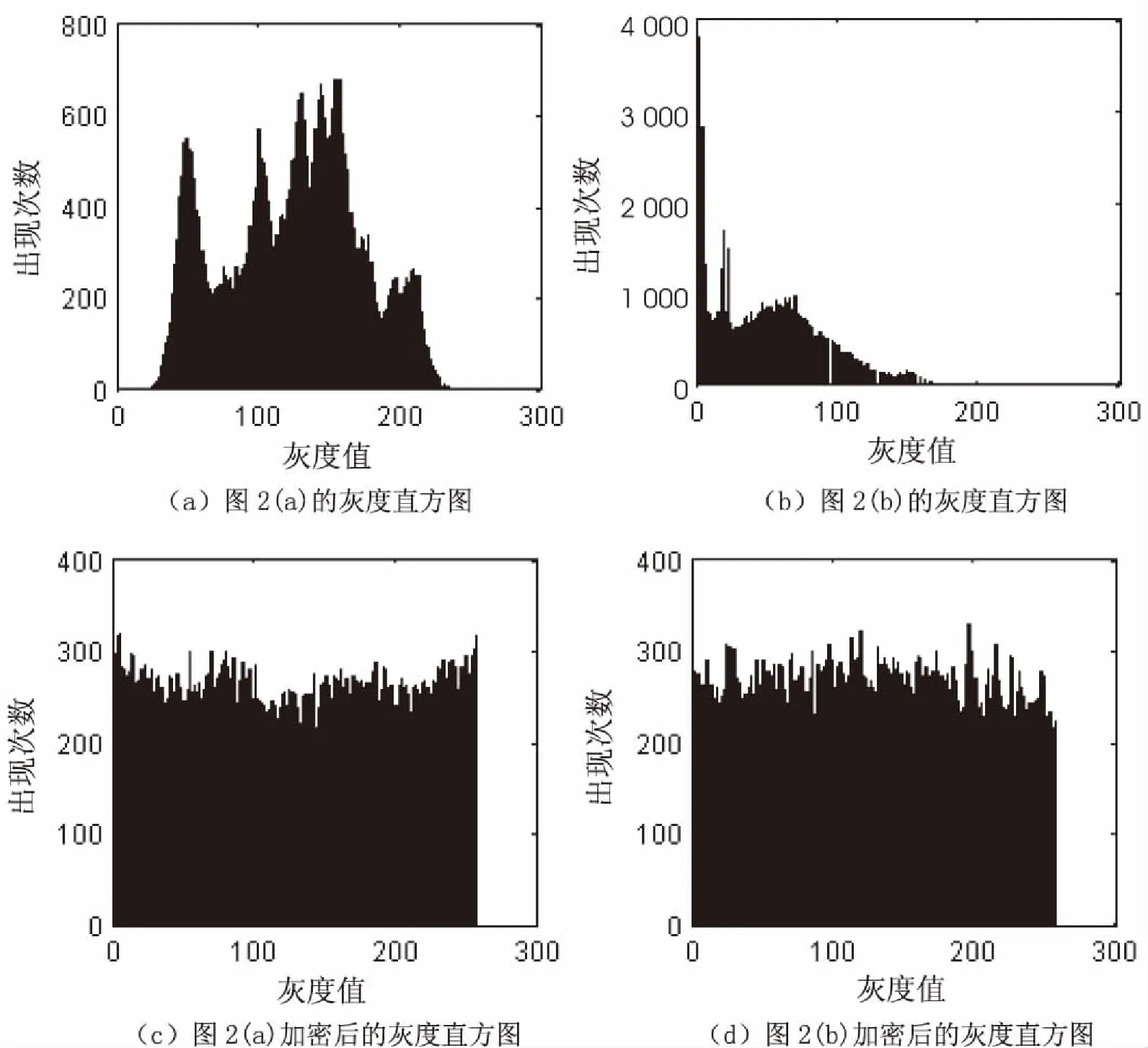
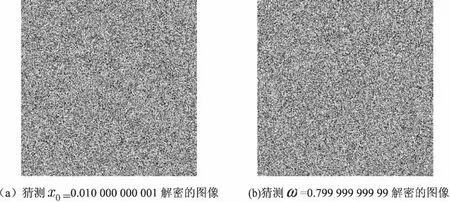
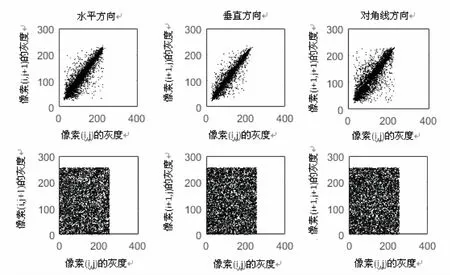
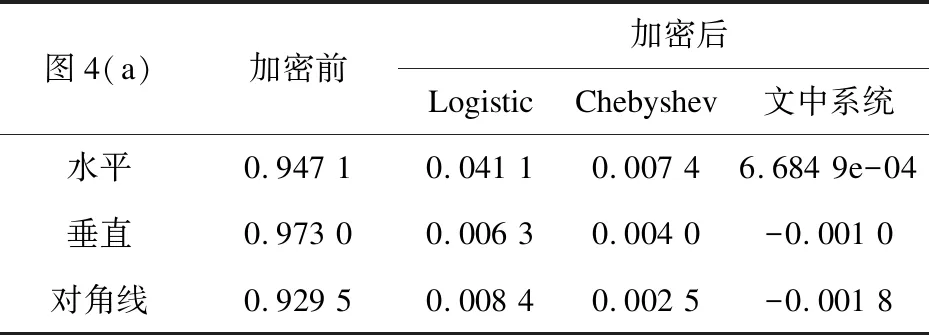
(1)设置初值x0和ω,其中0

(2)对有理映射函数(式3)进行N次预迭代；

(3)读取当前像素I(i,j)；

(4)将有理映射函数迭代8次，得到一个8位加密因子key；

(5)将key与图像当前灰度值I(i,j)按位异或，并将运算的结果写入I'(i,j)；

(6)如果I(i,j)是最后一个像素，转步骤7，否则，转步骤3；

(7)I'即为密文图像；

(8)结束。

2.3 解密算法

解密算法和加密算法是一套算法，也就是说，采用文中算法进行加密的图像，用同样的算法即可对其进行解密。可以看出，文中算法具有复杂性低、加密效率高的优点。

3 仿真结果及分析

对文中算法进行仿真验证，取初始值x0=0.01，ω=0.8。这里用两张图片作为仿真用例，加密前后的对比图像如图2所示。

图2 加密前后的对比图像

3.1 灰度直方图

灰度直方图是对图像中灰度级分布统计，直方图越均匀，抗统计分析能力越强。图3展示了图2中两幅图像加密前后的灰度直方图。可以明显看出，加密前后直方图变化很大，用该系统加密后图像直方图非常均匀。

3.2 密钥空间及安全性分析

该系统有两个参数，x0和ω，若运算精度按10-16考虑，则系统初始条件组成的空间大小至少为1016×1016=1032。要想进行枚举攻击几乎是不可能的。

图3 加密前后图像的灰度直方图

假如攻击者想破解图2(a)的加密图像，正确初始值为x0=0.01，ω=0.8。假若攻击者的猜测初值x0=0.010 000 000 001,ω=0.8，则解密图像如图4(a)所示；若攻击者猜测初值x0=0.01，ω=0.799 999 999 99，则解密图像如图4(b)所示。可以看出，用文中模型加密的图片的安全性是非常高的。

图4 解密失败的图像

3.3 相关性分析

图像之所以不同于文本是因为图像像素间具有很强的相关性，攻击者会根据图像间的相关性进行统计分析，从而破解加密图像，所以，降低相关性是检验一个加密算法好坏的重要指标。因此，分别按水平方向、垂直方向以及对角线方向随机选取图像中的50行，50列的像素进行相关性计算，随机次数为5次。以图2(a)为例，实验结果如图5所示。从仿真结果可以看出，相对于明文图片来说，像素间的相关性非常高，而在加密图片中像素的相关性的强度显著降低，具有非常好的加密效果，很好地满足了实际应用需求，有较高的实用价值。

分别求取该图像加密前后在三个方向上的相关系数，并且将经典的Logistic系统和Chebyshev同样用上述算法对图像进行加密后求取相关系数，对比结果如表1所示。可以明显看出，用同一算法实现三种不同的混沌系统，该系统加密后图像之间的相关性最小，安全性更高。

图5 加密前后相关性对比图 表1 加密前后相关系数对比

图4(a)加密前加密后LogisticChebyshev文中系统水平0.947 10.041 10.007 46.684 9e-04垂直0.973 00.006 30.004 0-0.001 0对角线0.929 50.008 40.002 5-0.001 8

3.4 信息熵

信息熵是对信息随机性的度量，在图像中表示像素灰度值的随机性，图像的信息熵越大，信息的随机性越好。对任意图像I，其信息熵计算公式如下：

(6)

其中，L表示图像的灰度级；p(xi)表示第i个像素灰度值所占的比例。

图像信息熵的理想值是8。选取图2(a)为示例，表2是分别采用Logistic映射、Chebyshev映射和文中算法对原图和加密图像求取的图像信息熵的对比结果。可以看出，该系统加密后图像的信息熵更接近8。

表2 加密前后信息熵对比表

4 结束语

Bezier曲线广泛应用于工程设计中，将Bezier方法应用于图像处理是一项具有实际意义的工作。因此，文中提出一种基于有理二次Bezier曲线的数字图像加密算法，保留了一维混沌系统形式简单的特点。由于加密和解密是一套算法，所以该算法具有复杂性低、加密效率高的优点。通过仿真测试表明，利用该算法加密的图像，其灰度直方图较为均匀，加密图像中相邻像素之间的相关性强度与传统加密算法相比显著降低，取得了较好的加密效果。该方法对于将Bezier方法应用于图像处理的其他问题也具有一定参考价值。