基于Kendall tau距离的在线服务信誉度量方法
郑苏苏 付晓东,2 岳 昆 刘 骊 刘利军 冯 勇
1(云南省计算机技术应用重点实验室(昆明理工大学信息工程与自动化学院) 昆明 650500)2(昆明理工大学航空学院 昆明 650500)3 (云南大学信息学院 昆明 650091)
随着互联网的发展和普及,传统商业环境向开放、共享、多元的面向在线服务方式转化.在线服务在电子商务、企业经营、管理等领域发挥越来越重要的作用.同时,随着互联网上可供用户选择的在线服务越来越多,用户也需要花费更多的时间和精力来寻找自己需要的服务[1-2]:首先,庞大的在线服务数量使得用户不可能与每个在线服务具有交互的经验,用户不可能获得每个在线服务的完整信息;其次,由于网络环境下允许匿名交互而彼此之间又不直接接触,某些用户或在线服务提供者可能提供不真实的服务信息[3-4].因此,用户通常需要借助以第三方观点为基础形成的在线服务信誉为辅助进行服务选择.
信誉是服务若干信用行为累积的结果,对于在线服务选择起着重要的作用[5].一种客观的在线服务信誉度量方法可有效地辅助用户进行在线服务的优劣选择决策.现有的在线服务信誉度量方法均假设所有用户根据相同的标准来评价服务,而未考虑到用户因主观偏好导致的评价准则不一致的问题[6].然而,受到自身习惯、生活经验和消费历史的影响,用户对在线服务评价的标准不可能完全相同.比如,有些用户倾向于给服务较高的评分,有些用户倾向于给服务较低的评分,导致即使本质表现相同的服务也会得到不同的评分[7].因此,不同用户对同一服务的评分不可比较,不考虑用户评分可比较性得到的服务信誉也不具备公正的可比较性.此外,一些用户和在线服务提供者为了获取不当利益,通过对某些服务提高评分或降低评分来达到操纵服务信誉的目的[8].利用这种信誉进行服务选择会对用户产生误导,使用户难以获取真正需要的服务.
为解决上述问题,本文提出了一种基于Kendall tau距离[9]的在线服务信誉度量方法,方法不需要假定用户具有相同的评价准则,考虑了用户对不同服务之间的关系,将与用户-服务评分矩阵Kendall tau距离最小的信誉向量作为最终的服务信誉,有效地避免了在线服务信誉不可比较的问题.
1 相关工作
近年来,国内外学者围绕更加精确、理性的在线服务信誉度量展开了一系列研究,目前的在线信誉度量方法主要有[1,10]:平均法模型、累加法模型、基于贝叶斯网络的信誉模型、离散的信誉模型、基于模糊逻辑的信誉模型、基于链状的信誉模型和基于证据理论的信誉模型等.文献[11]指出服务信誉度量可以分为2类:1)通过用户评分计算服务信誉;2)通过综合多种服务质量因素计算服务信誉,如响应时间、可用性和吞吐量等.
通过用户评分计算服务信誉的方法在目前的电子商务平台应用广泛[1].eBay网站采用求和法(SUM),将所有用户对服务的评分进行求和得到服务信誉,用户根据服务信誉对在线服务做出选择.Amazon网站则使用平均法(AVG),通过计算所有用户对服务评分的平均值得到其服务信誉.文献[12]提出了一种基于低阶矩阵分解的信誉估计方法,通过用户对项目的评分计算项目的信誉;文献[3]提出了一种计算评估者信誉的方法,根据评估者的评分历史和其他评估者对该评估者的评分自动计算评估者的声誉,并结合这些声誉来生成关于评分对象的增值信息;文献[13]提出了一种基于上下文的Web服务信誉测量方法,根据用户的上下文对评分进行分类,然后根据用户评分差异获得用户的内部评分,最后采用基于用户的协同过滤衡量每个Web服务的声誉.
通过用户评分计算服务信誉只考虑用户对服务的主观感受并未考虑到影响服务信誉的其他因素[14],比如服务质量(quality of service, QoS)、用户历史行为、社交网络关系等.文献[15]提出一种基于服务质量相似度的Web服务信誉度量模型,通过比较服务质量公告值和实际值的相似性来进行Web服务信誉评估.文献[16]提出一种用QoS感知Web服务选择中信誉度评估的方法,通过反馈核查、校正和检测这3个信誉度评估模块对服务的信誉度进行评估.文献[17]提出了一种基于云的评价方法,通过评估服务消费者的历史行为,并考虑评分相似度以生成评分质量云,进而利用云模型的参数进行服务信誉评估.文献[18]提出了一种信誉管理系统,基于N元语法学习方法对社交媒体数据进行分析,以测量给定公司的声誉.文献[19]提出隐马尔可夫模型(hidden Markov model, HMM)来预测服务提供商的声誉,当客户的反馈不容易获得时,可以通过HMM综合一整套质量参数获得Web服务的声誉.
上述研究在进行服务信誉度量时都假设所有用户的偏好相同,并且他们能按照一致的评价准则对在线服务进行客观的评价[1].然而,在开放的在线网络环境中,用户对在线服务的偏好不可能完全一致,甚至可能出现矛盾和冲突.因此,上述研究提出的信誉度量方法忽视了用户评价准则不一致的问题,难以客观地反映在线服务的真实信誉.考虑到以上研究中存在的不足,本文充分考虑了用户的主观偏好不一致性,在不假设用户评价准则相同的情况下,提出一种基于Kendall tau距离的在线服务信誉度量方法.方法不考虑用户评分强度,而是将用户对不同服务的评分转化为用户对不同服务之间的偏好关系,将这些偏好关系进行集结,最终形成服务信誉.通过考虑用户对不同服务评分的关系,使得到的在线服务信誉具备可比较性.最后,本文通过理论分析与实验验证了方法的合理性和有效性.
2 问题描述
2.1 问题定义
为解决用户对服务评价准则不一致导致的服务信誉不具备可比较性的问题,本文首先对在线服务信誉度量问题进行定义.
定义1. 集合U={u1,u2,…,ux}为所有用户的集合,集合S={s1,s2,…,sy}为所有在线服务的集合,集合C={c1,c2,…,ch}为用户对在线服务的评分等级.其中,x为用户的个数,y为在线服务的个数,用户对在线服务的评分等级共有h种.
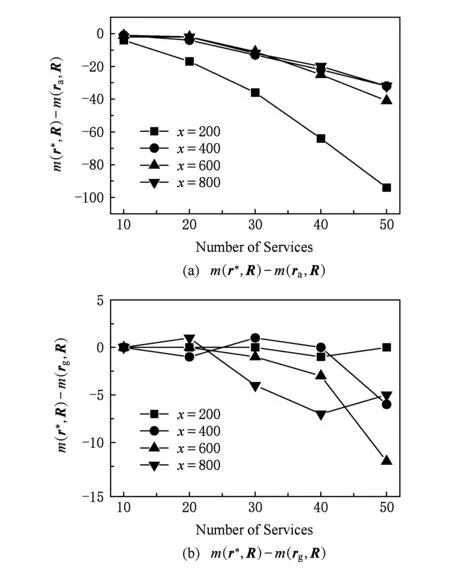
定义2. 评分向量ri=(ri 1,ri 2,…,ri p,…,riy)表示用户ui对所有服务的评分信息,ri p表示用户ui对服务sp的评分并体现用户ui对服务sp的满意程度.ri p越大则表示ui对sp越满意.ri p>ri q表示用户ui认为服务sp优于sq;ri p 定义3. 所有用户对服务的评分信息用矩阵R=(ri p)x×y表示,评分向量ri(i=1,2,…,x)的集合用G表示,即G={r1,r2,…,rx}. 定义4. 服务集合S={s1,s2,…,sy}的信誉用信誉向量rz=(rz1,rz2,…,rzy)表示,rz1,rz2,…,rzy分别表示服务s1,s2,…,sy的信誉值,且rz1,rz2,…,rzy属于集合C. 例1. 假设有3个用户(u1,u2,u3)共同对4个在线服务(s1,s2,s3,s4)进行评分,用户-服务评分矩阵R=(ri p)3×4如表1所示.其中评分ri p表示用户对在线服务的满意程度,采用电子商务评价机制中常用的5个评分等级,1~5分别表示很不满意、不满意、一般、满意和很满意.ri p=0表示该用户未与该服务产生交互或未对服务进行评分. Table1 Ratings Matrix of User-Service表1 用户-服务评分矩阵表 由表1可见,对于同一服务s4,用户u1对服务s4给出5分的评分,用户u2对服务s4给出3分的评分,并不能说明服务s4为用户u1提供的服务优于为用户u2提供的服务.由于不同用户对在线服务的偏好不同,面对表现相同的在线服务,不同用户也可能给出不同的评分.而对于同一服务s2,用户u1和用户u2都给出1分的评分,并不能说明服务s2对用户u1和用户u2的表现相同.因此即使服务表现不同,不同用户也可能给出相同的评分. 传统的服务信誉度量方法没有考虑到由于偏好不同导致用户评价准则不一致的问题.比如,平均法假定不同用户对在线服务的评价准则相同,通过计算所有用户对服务评分的平均值得到其服务信誉,得到的信誉向量为ra=(1.5,1.3,3.7,3.7).从信誉向量ra中可以看出平均法计算得到的服务s1优于服务s2,在基于信誉进行服务选择时,用户应该选择服务s1.然而在真实的在线网络环境中,不同用户对服务的偏好是不同的,即使服务s1,s2的表现相同,它们得到的评分依然可能不同,进一步导致最终得到的信誉不一样,也就是说服务s1,s2的信誉事实上不具有可比较性.其次,从信誉向量ra中可以看出服务s3,s4的信誉相同,而表1中所有用户对服务s3,s4的评分均不相同,因此根据平均法计算得到的信誉不具备可比较性,不能体现出用户的偏好.此外,如果将用户u1对服务s2的评分提高至5分,根据平均法得到的服务s2的信誉将提高至1.6分,并且对其他服务的信誉没有影响,使得服务s2的信誉大大提升,抗操纵性较弱.因此,本文提出一种基于Kendall tau距离的在线服务信誉度量方法,避免了用户评分准则不一致导致的在线服务信誉不可比较的问题,同时提高了信誉度量方法的抗操纵性. 由于用户评价准则不一致,不同用户的评分不具备可比较性,从而根据不同用户的评分计算得到的服务信誉也不具备可比较性.而对于同一理性用户,其对不同服务的评分是可以比较的.例1中用户u1对服务s3给出2分的评分,对服务s4给出5分的评分,可以推断用户u1认为服务s4优于服务s3,因此,通过考虑同一用户对不同服务评分之间的关系可以建立可比较的信誉度量方法. 基于以上分析,本文针对用户评价准则不一致导致的在线服务信誉不可比较的问题,提出一种基于Kendall tau距离的在线服务信誉度量方法.Kendall tau距离通过计算2个排列之间的逆序数来衡量2个排列π和σ之间的差异程度[20],计算方法为 K(π,σ)=|(i,j):i (1) 其中,π[i]和σ[i]分别表示元素i在排列π和σ中的排名.从式(1)可以看出,排列π和σ之间的Kendall tau距离为元素i和元素j在2个排列中的排列顺序不一致的数量. 我们将Kendall tau距离重新定义以测量2个服务评分向量之间用户对成对服务偏好不一致性的数量,距离越小,2个服务评分向量越一致[21-22].本文通过Kendall tau距离比较同一用户对不同服务的评分,将与用户-服务评分矩阵距离最小的信誉向量作为与所有用户偏好最一致的服务信誉.由于同一用户的评分是可以比较的,因而可以有效地避免用户评价准则不一致导致的在线服务信誉不可比较的问题.同时,通过考虑用户对不同服务评分的关系,提高了信誉度量方法的抗操纵性.此外,本文采用模拟退火算法(simulated annealing, SA)寻找最优信誉向量,有效地避免了陷入局部最优的缺点,保证了信誉度量方法的效率. 定义5. 距离指标K(ri,rj)用来表示2个服务评分向量ri=(ri1,…ri p,…,ri y),rj=(rj1,…rj q,…,rj y)之间的Kendall tau距离. 我们用K(ri,rj)表示ri,rj之间的偏好一致性:K(ri,rj)越小,表示ri,rj之间的偏好一致性越大;K(ri,rj)越大,表示ri,rj之间的偏好一致性越小;K(ri,rj)=0表示ri,rj之间的偏好完全一致. 计算K(ri,rj)首先要计算对于每2个服务ri,rj之间的距离,对于2个不同的服务sp,sq∈S(p≠q),它们在2个服务评分向量ri,rj之间的距离表示为 (2) 例1中r11=r12并且r21>r22,此时Ks1,s2(r1,r2)=1,表示从评分向量r1,r2可以看到,用户u1,u2对服务s1,s2具有不同的偏好.另一方面,由于r11 对服务集合S={s1,s2,…,sy},计算2个服务评分向量ri,rj之间的距离可通过计算针对ri,rj的距离之和得到.即: (3) 例1中2个评分向量r1,r2之间的距离K(r1,r2)=Κs1,s2(r1,r2)+Ks1,s3(r1,r2)+Ks1,s4(r1,r2)+Ks2,s3(r1,r2)+Ks2,s4(r1,r2)+Ks3,s4(r1,r2)=2,表示评分向量r1,r2之间用户对2对不同服务的偏好不一致.其中Ks1,s2(r1,r2)=1,表示用户u1和u2对服务s1和s2具有不同的偏好.r13 Kendall tau距离是衡量评分向量之间的成对分歧数量的指标,距离越小,2个评分向量越一致.本文服务信誉度量方法的核心是找到一个与所有用户偏好最一致的信誉向量,即与用户-服务评分矩阵R之间距离最小的信誉向量.因此我们首先根据距离指标K(ri,rj)的定义计算信誉向量rz和用户-服务评分矩阵R之间的距离. 定义6. 距离指标K(rz,R)用来表示信誉向量rz=(rz1,rz2,…,rzy)和用户-服务评分矩阵R之间的Kendall tau距离. K(rz,R)表示信誉向量rz和用户-服务评分矩阵R之间的偏好一致性:K(rz,R)越小,表示rz,R之间的偏好一致性越大;K(rz,R)越大,表示rz,R之间的偏好一致性越小;K(rz,R)=0表示rz,R之间的偏好完全一致. 对于y个在线服务、h个评分等级,有hy种可能的信誉向量,如果一一计算每个可能的信誉向量与用户-服务评分矩阵R中每个评分向量的距离之和,计算量庞大且运行时间长,因此本方法预先统计用户-服务评分矩阵R中ri p>ri q,ri p=ri q,ri p 计算K(rz,R)首先要计算对于每2个服务rz,R之间的距离,对于2个不同的服务sp,sq∈S(p≠q),它们在信誉向量rz与用户-服务评分矩阵R之间的距离为 (4) 对服务集合S={s1,s2,…,sy},rz与用户-服务评分矩阵R之间的距离通过计算rz,R之间距离的和得到.即: (5) 计算例1中对服务集合S={s1,s2,s3,s4}信誉向量ra与用户-服务评分矩阵R之间的距离.首先统计|Vp q|,|Vp p|,|Vq p|的数量;然后根据式(4)计算得出对于每2个服务在ra,R之间的距离;最后求和得到K(ra,R)=4,表示ra,R之间对成对服务偏好不一致的数量为4. 基于以上分析,确定信誉度量最优化目标函数为 (6) 寻找最优信誉向量是一个NP难问题[21],解空间规模随在线服务数量y的增大呈指数增加,利用传统的穷尽搜索方法寻找最优向量需要计算每一种可能的信誉向量与用户-服务评分矩阵之间的距离,并将距离最小的信誉向量作为服务信誉,计算量庞大且对存储空间需求很大.文献[21]提出用遗传算法(genetic algorithm, GA)解决此类优化问题.然而由于遗传算法的局限性,容易产生“过早收敛”的问题,即很快收敛到局部最优解,而不是全局最优解[23].模拟退火算法是一种随机搜索方法,在寻优过程中具有概率突跳性,除了可以接受优化解外,还可用Metropolis准则有限度地接受较差解,并且接受较差解的概率慢慢趋向于0.由于在整个解空间内取值的随机性,可以改善陷入局部最优解的缺陷,使算法尽可能地收敛于全局最优解,已经被证明可以在多项式时间内解决复杂的组合优化问题[24-25].因此本文将采用模拟退火方法作为寻优算法,寻找最优信誉向量.步骤为 ① http://www.grouplens.org/node/73 步骤1. 设定模拟退火算法的参数,包括初始温度t0、终止温度te、退温系数α、Markov链长L.令终止条件为:温度t下连续m次迭代过程中的新解都未被接受或者温度降为终止温度,满足其中任一条件则计算终止. 步骤2. 设定初始解r0,从解空间M中随机选取1个可能解作为初始解r0,r0=(r01,r02,…,r0y),计算r0的目标函数值K(r0,R). 步骤3. 随机改变初始解r0中的部分元素值(如改变r02和r04的值),产生1个位于解空间M的新解rn,rn=(rn1,rn2,…rny),计算rn的目标函数值K(rn,R). 步骤4. 计算rn的目标函数K(rn,R)与r0的目标函数K(r0,R)之间的差值Δk,Δk=K(rn,R)-K(r0,R). 步骤5. 新解的接受概率为 (7) 其中,t为当前温度,降温后的温度T=αt.新解的接受遵循Metropolis准则:当Δk<0时,接受rn作为当前最优解;当Δk>0时,给出一个(0,1)区间上的随机数β,在新解的接受概率P>β时,接受rn作为当前最优解,否则不接受rn,此时初始解r0实现了一次迭代.在当前温度下共进行L次迭代,若迭代过程中接受了新的解,则不满足终止条件,根据T=αt降低温度. 步骤6.令当前温度t=T,重复步骤3~5,直到满足终止条件,此时停止计算,求得的当前解r*为最优解. 步骤7.将得到的最优解r*作为用户-服务评分矩阵R的服务信誉. 由于退火参数对求解优化问题有很大影响,因此我们设置合理的退火参数,根据不同的服务和用户规模设置算法终止条件.终止条件之一为温度t下连续m迭代过程中的新解都未被接受.在用户和服务规模较小时,由于运行速度快,可以设置较大的m值以保证得到最优信誉向量;随着用户和服务规模越来越大,可能产生的新解rn越来越多,此时m值可以适当减小,以提高算法的寻优效率. 为了尽可能地获得最优解,我们在算法中加入补充搜索环节,在得到最优解r*后,可以将r*作为初始解r0进行新一轮的寻优过程,得到与用户-服务评分矩阵距离更小的最优信誉向量. 将以上步骤应用到3.2节例1中,得到最优信誉向量为r*=(1,1,5,4),r*与用户-服务评分矩阵R之间的Kendall tau距离为K(r*,R)=2.而用平均法得到的信誉向量ra=(1.5,1.3,3.7,3.7),与用户-服务评分矩阵R之间的Kendall tau距离为K(ra,R)=4.由此可见,本文方法得到的信誉向量与平均法相比,与用户-服务评分矩阵间的距离更小,从而与所有用户具有更大的偏好一致性.此外,如果将用户u1对服务s2的评分提高至5分,根据本方法得到的最优信誉向量为r*=(2,3,5,4),对服务s2操纵不仅提高了s2的信誉,服务s1的信誉也会提升,因此本方法具有更强的抗操纵性. 根据第3节提到的基于Kendall tau距离的在线服务信誉度量方法,设计实现了在线服务信誉度量方法,用于在线服务信誉度量,并对评价数据进行验证.实验环境为PC机,Windows 8系统、Core i5处理器、8 GB内存. 为验证本文信誉度量方法的有效性和效率,我们采用MovieLens①数据集,包含1 682部电影、943个用户以及100 000条左右的评分(1~5),每个用户至少对20部电影进行过评分.由于用户对电影的评分稀疏,为确保信誉度量的高效性,如果每对服务中至少有一个服务未被评分,实验中将忽略这对服务的比较.由于平均法易于理解并且被广泛应用于计算服务信誉[1],因此我们将平均法作为本文的主要对比方法.文献[21]提出用遗传算法解决信誉计算中的组合优化问题,并通过理论及实验证明了其合理性.遗传算法也是一种有效的近似优化算法,为了测试本文模拟退火算法的性能,实验对比了遗传算法和本文算法的优化效果和运行效率.其中,用r*表示用本文方法求得的信誉向量,用ra表示用平均法求得的信誉向量,用rg表示用遗传算法求得的信誉向量. 在实验中,我们需要设置合理的模拟退火参数:初始温度、终止温度、退温系数和Markov链长.如果这些参数设置得太小,不能进行高质量的寻优计算,很难得到最优信誉向量;如果设置得太大,则运行时间过长,迭代运算速度慢,浪费大量不必要的计算资源.为了提高算法得到最优信誉向量的可靠性,实验过程中将初始温度和终止温度设置为常用的参数[26],t0=100,te=1,并且设置退温系数α=0.9,Markov链长L=10. Fig. 1 Consistency verification图1 一致性验证 根据式(4),信誉向量与用户-服务评分矩阵R的Kendall tau距离越小,表示该信誉向量与所有用户的分歧越小,与所有用户的偏好越一致,因此将与用户-服务评分矩阵R的Kendall tau距离最小的信誉向量作为服务信誉是合理的.因此,我们用Kendall tau距离验证方法的有效性.实验模拟了200~800个用户和10~50个在线服务,在不同用户数量x和不同服务数量y下,记录依据本文方法得到的最优信誉向量r*与用户-服务评分矩阵R间的Kendall tau距离K(r*,R)、平均法得到的信誉向量ra与用户-服务评分矩阵R的Kendall tau距离K(ra,R),以及依据文献[21]中的遗传算法得到的最优信誉向量rg与用户-服务评分矩阵R的Kendall tau距离K(rg,R),如图1所示. 由图1可见,随着用户数量和服务数量的增加,K(r*,R),K(ra,R),K(rg,R)都会增加.说明不可能得到与所有用户偏好完全一致的信誉向量,并且服务和用户规模越大,信誉向量与所有用户的偏好不一致性越大.这符合社会选择理论中的阿罗定理,当众多的社会成员具有不同的偏好时,不可能存在令所有人都满意的结果[27]. 此外,算法比较记录了不同样本规模下K(r*,R),K(ra,R) 的差值以及K(r*,R),K(rg,R)的差值,K(r*,R)-K(ra,R)如图2(a)所示,K(r*,R)-K(rg,R)如图2(b)所示: Fig. 2 Consistency comparison of reputation measurement methods图2 信誉度量方法一致性比较 由图2(a)可见,在同样的服务数量和用户规模下,K(r*,R)-K(ra,R)始终小于0,K(r*,R)始终小于K(ra,R),并且随着服务数量和用户规模的增大,K(ra,R),K(r*,R)的差值越来越大.说明根据本方法得到的信誉向量与用户-服务评分矩阵R之间的Kendall tau距离更小,在服务和用户规模一定时,采用本方法计算服务信誉比平均法更为合理,得到的信誉更符合用户的偏好. 由图2(b)可见,在用户数量为200、服务数量为10时,K(r*,R)-K(ra,R)=0.说明在用户服务规模较小时,模拟退火和遗传算法都能找到最优信誉向量.然而随着服务数量和用户规模的增大,K(rg,R)与K(r*,R)的差值越来越大,模拟退火算法总能找到比遗传算法更好的解,得到的信誉向量与R之间的Kendall tau距离更小,与所有用户的偏好更为一致. Fig. 3 Verification of majority rule图3 多数准则验证 服务信誉应满足大多数人的偏好,因此我们利用经济学理论中的多数准则验证方法有效性.这里的多数准则指的是如果存在认为服务si优于服务sj的用户多于认为服务sj优于服务si的用户,那么根据多数准则,由服务信誉度量方法得到的服务信誉应体现si优于sj.我们使用m(ri,R)表示信誉向量中不符合多数准则的数量,即ri p 由图3可见,无论是本文方法还是平均法得到的信誉向量中,ri p 此外,我们还记录了不同样本规模下m(r*,R),m(ra,R) 的差值以及m(r*,R),m(rg,R)的差值,m(r*,R)-m(ra,R)如图4(a)所示,m(r*,R)-m(rg,R)如图4(b)所示: Fig. 4 Comparison of majority rule of reputation measurement methods图4 信誉度量方法多数准则比较 由图4(a)可见,在不同用户数量和服务数量的情况下,m(r*,R)-m(ra,R)始终小于0,即m(r*,R)始终小于m(ra,R).说明本文方法得到的信誉向量中ri p>ri q并且用户-服务评分矩阵R中|Vp q|>|Vq p|的情况更少,比平均法更符合多数准则. 由图4(b)可见,在用户数量为200、服务数量为10时,m(r*,R)=0且m(rg,R)=0.说明在用户服务规模较小时,模拟退火和遗传算法得到的结果都能满足多数准则;而当用户和服务规模变大时,m(r*,R)在绝大多数情况下小于m(rg,R).模拟退火算法和遗传算法的寻优过程都具有随机性,然而本文使用模拟退火算法得到的信誉向量比遗传算法得到的信誉向量更符合多数准则. 为了验证该方法的操纵复杂性,随机选择3个在线服务,用户数量为800,并对其中某一服务增加高评分评价,若根据该方法得到的服务信誉排名无明显提升,则该方法具有较强的抗操纵性.假设有3个服务s1,s2,s3,有20%,40%,60%,80%,100%的用户对评分进行操纵,这些用户对服务s1的评分提高至5分,观察3个服务信誉的变化.本文方法的信誉如图5(a)所示,平均法的信誉如图5(b)所示: Fig. 5 Verification of manipulation resistance performance图5 抗操纵性能验证 根据图5(a)所示,随着操纵评分数量的增加,根据本文方法得到的服务s1的信誉值先提高再降低然后不变,并且当服务s1的信誉改变时,服务s2,s3的信誉也会随之改变.而根据图5(b)所示,根据平均值方法得到的服务s1的信誉值明显提升,但并不会改变服务s2,s3的信誉,从而实现了对服务s1的操纵.因此本方法更具抗操纵性. 为验证该方法的效率,实验模拟了200~800个用户和10~50个在线服务,在不同样本规模下算法记录了系统每次进行服务信誉度量的运行时间,如图6所示.同时,比较了在800个用户和10~50个在线服务规模下模拟退火算法、平均法、遗传算法和整数规划算法(mixed integer programming, MIP)的运行时间,如图7所示.整数规划算法计算所有可能的信誉向量的目标函数值,并将目标函数值最小的信誉向量作为最优信誉向量输出. Fig. 6 Runtime of different sample sizes图6 不同样本规模下的运行时间 根据图6所示,随着服务数量的增加,运行时间不断增加,即算法的效率逐渐降低.但是相同服务数量下,运行时间并不随着用户数量的增多而变长,这是因为,在服务数量一定时,只需预先计算|Vp q|,|Vp p|,|Vq p|的数量,之后再用式(3)计算信誉向量与用户-服务评分矩阵之间的距离,运行时间与用户数量无关.因此,在服务数量一定时,本文方法可以有效地提升信誉度量的效率. Fig. 7 Runtime of SA, MIP, AVG, and GA图7 SA,MIP,AVG,GA方法的运行时间 根据图7所示,当服务数量较少时,模拟退火算法、平均法、遗传算法和整数规划算法的运行时间并无太大差别.但当服务数量超过9时,整数规划算法的运行时间随着服务数量的增加呈指数增长,远远超过模拟退火算法的运行时间.在用户数量小于11时,本文的模拟退火算法获得的服务信誉与整数规划算法相比并无差别,对于大规模的用户和服务而言,模拟退火算法比整数规划算法效率更高.此外,模拟退火算法与遗传算法的运行时间并无明显差距,但模拟退火算法得到的信誉向量优于遗传算法得到的信誉向量.可见模拟退火算法在保证得到最优解的同时,克服了寻优速度慢的缺点.并且,与平均法相比,虽然本文方法的运行时间较长,但对信誉度量方法进行操纵比平均法消耗时长多,抗操纵性更强. 本文提出一种基于Kendall tau距离的在线服务信誉度量方法,以解决由于用户评价准则不一致导致的在线服务信誉不可比较的问题.方法采用Kendall tau距离指标来衡量2个评分向量的差异,然后将信誉度量转化为最优化问题,再采用模拟退火算法寻找最优信誉向量作为服务信誉,为在线服务的信誉度量提供了一种新的思路.理论分析及实验验证表明了该方法的有效性、抗操纵性以及高效性.本方法在信誉度量时只考虑了用户对在线服务的评分值,未能全面考虑影响信誉的多种因素.因此下一步的工作将结合影响服务信誉的其他因素,研究更加精确的在线服务信誉度量方法.2.2 举例说明

3 基于Kendall tau距离的在线服务信誉度量
(π[i]>π[j]∧σ[i]<π[j])|,3.1 基于Kendall tau的评分向量距离度量

3.2 基于Kendall tau距离的信誉度量





3.3 基于模拟退火算法寻找最优信誉向量

4 实验结果及分析
4.1 有效性实验



4.2 多数准则
4.3 抗操纵性

4.4 性能测试


5 结 语

