高泥质低阻碎屑岩储层含油饱和度评价方法
陈 静,郭 涛,朱龙权
(1.中国石油新疆油田分公司 石西油田作业区,新疆 克拉玛依 834000;2.四川海盾石油新技术开发有限公司,成都 610041)
低阻油层是指油层电阻率和相邻水层的电阻率差别不大的油层,其主要特征是油层的电阻率与邻近水层的电阻率之比<2[1-3]。在实际生产中,油井不含水或低含水,试油解释结论一般为“油层”。
大量勘探开发实践证明,低阻油层广泛存在于复杂砂岩油藏中。大庆、冀东、大港、华北、辽河和新疆油田等都发现有低阻油藏[4]。低阻油藏的成因,概括起来主要有[4]:高不动水含量的影响[5-6];储层润湿性的影响[6];裂缝型中低孔油藏受泥浆滤液侵入的影响[7];高泥质含量(黏土含量)油层因阳离子交换引起的附加导电性的影响[8];油层束缚水与水层矿化度差异的影响[8];砂泥岩薄互层中,油层受围岩的影响[9]。
自1997年以来,中国石油天然气公司组织专家对低阻油藏测井解释评价进行研究,总结了一套低阻油层识别和评价技术。该技术主要在理念和方法上给出了思路,但在实际应用中对技术人员要求高,现场可操作性受到限制,难以推广应用。针对老油田现有资料,建立一套有针对性的、应用常规测井技术的、操作性强的测井解释评价方法,对老油田低阻油藏评价具有重要意义。
石南31井区白垩系清水河组油藏是一个岩性控制的边水油藏,投入开发后,油井实际生产动态与测井解释结论存在矛盾:①部分油层电阻率较低,与邻近水层电阻率接近,常规测井解释无油层,但射孔投产后能较长时间保持无水生产,常规解释容易漏掉一些油层。②常规饱和度解释模型解释的含油饱和度普遍偏低,特别是油藏砂体边界和砂体沉积相变带的油井,测井解释含油饱和度50%左右,但油井长期保持无水生产,与本区相渗规律存在矛盾。③边水油藏的油水过渡带油水关系复杂,应用常规饱和度解释模型,导致部分水层解释含油饱和度高于油层,还有部分水层电阻率高于油层电阻率,常规测井解释难以有效区分这部分油水层(图1)。
因常规测井解释对这类油层解释的局限性,导致油藏开发中容易误射、漏射,影响油藏开发效果;并且储量计算不准确,影响开发决策。
1 石南31井区低阻油层成因
1.1 微孔隙发育的影响
石南31井区储层孔喉统计直方图存在双峰特征, 孔喉半径主要在0.1~2.5 μm, >4 μm的喉道所占比例<20%,储层孔喉分选性较差,存在较强非均质性(图2)。储层中微孔隙发育,<0.16 μm的孔隙所占比例达到20%;岩心分析束缚水饱和度为47.3%~73%,平均为60%;油层电阻率为10 Ω·m,邻近水层电阻率与油层接近:属于典型的微孔隙型高束缚水低阻油层。
1.1.1 微孔隙发育成因
准噶尔盆地各油田储层沉积以冲积扇、扇三角洲为主,储层岩性主要为砂砾岩和砾岩,粒度分布范围大,导致储层孔隙结构复杂,微孔隙发育。
储层微孔隙发育程度受岩性颗粒大小、粉砂质含量影响。针对石南31井区,当储层粉砂质(粒度0.003 9~0.063 mm)体积分数>10%时,储层中值孔喉半径为0.66 μm;当粉砂质的体积分数>15%时,储层中值孔喉半径为0.09 μm。孔喉中微细孔所占比例增高,储层渗透率明显降低:粒径>0.063 mm的颗粒体积分数≥90%时,渗透率平均值为117.54×10-3μm2;>0.063 mm的颗粒体积分数<90%时,67%的样品渗透率只有(0~5)×10-3μm2,平均为19.3×10-3μm2(图3)。
1.1.2 微孔隙对电阻率的影响
从机理上讲,微孔隙发育对油气层电阻率的影响主要表现在2个方面。
a.受微孔隙强大的毛管力影响,束缚水饱和度增加,油层电阻率偏低[6]。统计准噶尔盆地6个微孔隙较发育区块的岩心束缚水饱和度,平均为33%~60%, 表明并不是所有微孔隙发育储层均有较高的束缚水饱和度,还有其他因素影响微孔隙发育油层的电阻率。
b.微孔隙引起的储层胶结指数变化。假设有2块岩心样品(图4),地层水矿化度、孔隙弯曲度、电流传导路径均一致,A样品孔隙度为q1,B样品的孔隙直径是A样品的x倍,样品A的胶结指数为m1,样品B的胶结指数为m2,岩石电导率分别为σ1和σ2,根据导电机理有
(1)

式中:σ1和σ2为样品电导率;q1为样品总孔隙度;m1和m2为岩石胶结指数;x为样品B相对于样品A的孔隙度倍数。

图1 新疆油田某区块W02井试油结论与综合解释成果Fig.1 Formation testing and comprehensive interpretation for drilling well W02 in a block of Xinjiang Oilfield

图2 某区块孔隙半径分布直方图Fig.2 Histogram showing the distribution of porosity diameter in certain blocks
分析表明,当储层中微孔隙较发育时,储层岩石胶结指数会减小。
又假设储层由纯净砂岩组成,泥质含量为0,用阿尔奇公式计算,不同的胶结指数对含油饱和度计算结果影响大,胶结指数从1.5增大到1.8,含油饱和度降低约10%(表1)。
1.2 泥质含量的影响
a.黏土矿物的附加导电作用引起油气层电阻率偏低。
关于黏土矿物的阳离子交换能力及其对电阻率的影响,雍世和等[10]做了系统的讨论;M.H.Waxman等提出了著名的泥质砂岩电导率模型,一般被称为Waxman-Smits模型[11],该模型认为泥质砂岩中,由于黏土的吸附作用引起黏土矿物附近大量聚集阳离子,又由于阳离子交换作用,产生明显的附加导电性, 致使泥质砂岩油气层电阻率显著降低。 之后, 更多的人做了相关的实验研究,发现储层中伊利石质量分数>4%,就能将油层电阻率降至10 Ω·m以下,形成低阻油层。

图3 粉砂质粒径的颗粒含量对储层渗透率的影响Fig.3 Influence of grain content of silty particle size on reservoir permeability (A)粒径>0.063 mm的砂质体积分数≥90%; (B)粒径>0.063 mm的砂质体积分数<90%

图4 样品A和样品B剖面示意图Fig.4 Profile illustrating sample A and sample B

表1 理论计算胶结指数与含油饱和度的关系Table 1 Correlation of theoretical cementation exponent and oil saturation
b.黏土矿物的阳离子吸附作用,会导致黏土孔隙空间中的黏土水矿化度与自由水的矿化度有一定差异。黏土附近双电层吸附阳离子,容易造成这部分水膜中具有较高的离子浓度,而自由水中的离子浓度低于原生自由水离子浓度,最终导致自由水的矿化度比黏土水更低。
需要注意的是,尽管泥质含量会对储层电阻率有重要影响,但并非所有泥质砂岩都具有较高的阳离子交换能力,这与黏土矿物的成分有较大的关系。表2统计了常见黏土矿物的阳离子交换能力,可以看到,高岭石的阳离子交换能力相对较低,因此,以高岭石为主的黏土矿物,若油气层电阻率偏低,其原因更大的可能是由于微孔隙发育或砂泥薄互层等因素影响。

表2 不同黏土矿物的阳离子交换容量Table 2 Cation exchange capacity of different clay minerals
2 石南31井区低阻油层的系统解决方案
根据因素分析表明,石南31井区低阻的成因主要是泥质含量高、微孔隙发育,针对这种地质特征,在反复试验的基础上,认为采用双水模型是一个较好的解决方案。
2.1 双水模型
根据C.Clavier等的研究结果[12],双水模型表示为
(2)
其中
(3)
(4)
(5)
(6)
(7)
公式中各参数的含义如下:σt为地层真电导率;σw为地层孔隙中自由水的电导率;σbw为黏土束缚水电导率;σNa为黏土水中补偿离子Na+的等效电导率;a为孔隙迂曲度指数;qt为总孔隙度(体积比);m*为经过校正的岩石胶结指数;n为饱和度指数;Swt为总含水饱和度(体积比);Swb为黏土束缚水饱和度(体积比);α为Na+离子扩散层扩展因子;Pw为地层水矿化度;Pwc为常数(=0.35 mol/L);Vq表示Qv=1 mol/L时,黏土水占据的孔隙体积;φbw为孔隙中黏土束缚水的体积分数;Qv为阳离子交换容量,表示单位孔隙体积中的可交换阳离子摩尔数;φci为第i种黏土矿物的体积分数;ρci为第i种黏土矿物的骨架密度;t为地层温度;Cci为第i种黏土矿物的阳离子交换容量;nc为黏土矿物种类总数。
上述公式中,α根据矿化度求取,Vq和β通过地层温度求取。
从形式上看,双水模型等同于将自由水电导率和黏土束缚水电导率按照各自所占百分比加权求取了一个综合电导率,然后,按照阿尔奇公式计算含水饱和度。
尽管双水模型在以往的应用中有不少成功的经验,使之成为目前广泛认可的泥质砂岩饱和度电导(阻)率模型;但也有学者研究认为,双水模型仍然存在一些不足之处。曾文冲等指出,在低矿化度地层水的储层中,比起阿尔奇公式,泥质砂岩电导率模型能更好地评价储层含油饱和度[6-7];而黄布宙等通过实验分析发现,在低矿化度地层水储层中,若泥质含量较高,使用双水模型计算的储层含油饱和度仍然偏低[13]:因此,需要对其进行参数校正。
从双水模型的参数和前文分析低阻油气层的成因看,使用双水模型评价储层饱和度,还有3个重要问题需要分析:泥质含量、粉砂质含量和模型参数的适应性。
2.2 泥质和粉砂质含量的求取
石南31井区白垩系清水河组(K1q)储层主要以砂砾岩和砾岩为主,岩石薄片鉴定表明,在沉积碎屑物中,火山岩碎屑含量高,对GR测井值影响较大,部分泥质含量低的储层段,GR值却较高。其中泥质含量低的K1q11-2层GR值比泥质含量高的K1q11-3层高,因此本区不能用GR曲线计算泥质含量;电阻率曲线因受含油性影响,求取泥质含量准确性相对较低;SP曲线通常存在泥岩基线漂移的问题。使用SP曲线计算泥质含量,在准确性要求不高的情况下,可以采纳;但对于需要使用泥质含量对饱和度进行精确校正的情况下,这种方法的处理结果往往不尽人意,存在很大误差。
经过大量实践,笔者认为,采用岩性体积含量反演的方法求取泥质含量,能极大地提高泥质含量的准确性,进而更加精确地评价含油饱和度。
传统的多矿物联合最优化解释方法,是以组成岩石的矿物成分为基础,以矿物成分的固有物理性质作为骨架参数,其侧重点在于准确评价孔隙度和含油饱和度,但并不强调计算结果中泥质含量的准确性。这是因为,“泥质”是一个综合概念,它并不代表某一种单一的黏土矿物,而是由多种矿物共同组成。通常,“泥质”中不仅有高岭石,也有绿泥石、伊利石、蒙脱石等各种黏土矿物,因此,使用双矿物模型或多矿物模型,并不能有效地解决泥质含量计算准确性的问题。
研究发现,对于同样的沉积环境,“泥质”的组成成分,往往具有较高的一致性,即同一油藏中“泥质”的主要成分保持稳定。以石南31井区为例,其主要组成矿物为伊蒙混层(约67%),且在不同的样品中,这个比例基本保持稳定。这就为岩性体积含量反演提供了基本依据。
本文提出“岩性体积含量反演方法”,不同于以往研究中的双矿物或多矿物最优化解释方法。它以岩心粒度分析和岩石薄片分析为依据,以“依靠沉积粒度分类”、并且具有相似矿物组成的岩石(岩性)为基础,通过研究不同岩性的骨架参数,利用最优化测井反演方法,求取不同岩性的体积分数。其优势在于:①可以准确地求取泥质含量,而不是单一的某一种黏土矿物含量;②可以准确地求取粉砂质成分的含量,为含油饱和度评价提供依据。
岩性体积含量反演的基本公式如下
(8)
其中:φi为第i种成分的体积分数;φw为水(包括所有束缚水、可动水等所有类型的地层水)的体积分数;φo为烃类的体积分数;Pi为第i种成分的岩石骨架参数;ci为第i条测井曲线;Constraints表示其他约束条件。
φi即为需要求取的某种成分的体积分数。根据公式(8),使用密度(DEN或RHOB)、中子(CNL或NPHI)、声波(AC或DT)、伽马(GR)、地层真电阻率(RT)和冲洗带电阻率(RXO)共6条互相独立的测井曲线,可以求取7种不同成分的体积分数。
依据沉积和储层特征,将石南31井区储层分解为泥质、粉砂质、细砂质、中砂质、粗砂质、砾质和钙质7种成分。在研究组成岩石的矿物成分的稳定性基础上,通过反复试验,取粒度分析中每种粒度成分最纯净(单一粒度成分的占比超过80%)的样本深度段,读出它们在测井曲线上的典型测井响应特征,联合岩心分析的孔隙度和含油饱和度值,计算其骨架参数Pi,然后建立起公式(8)所示的方程组,求解各种成分的相对体积分数。
为使反演结果更加准确可靠,统计岩心粒度分析数据,建立以下约束方程
φ砾=-1.0098×φ砂+泥+0.8709,R2=0.9853
(9)
φ中砂=-0.8619×φ细砂+粗砂+泥+0.7836,R2=0.9395
(10)
其中:φ砾为砾质(粒径>2 mm)成分的体积分数;φ砂+泥为粒径<2 mm的所有成分的体积分数总和;φ中砂为中砂质(0.25 mm<粒径≤0.5 mm)成分的体积分数;φ细砂+粗砂+泥为粗砂质(0.5 mm<粒径≤2 mm)和粒径<0.25mm的成分的体积分数总和。
应用岩性体积含量反演方法可以较好地求出储层泥质和粉砂质(粒径<0.063 mm)含量,求解结果与岩心分析结果的对比如图5(最后一道)所示。
2.3 双水模型的参数求取
2.3.1 胶结指数的泥质校正
对于高泥质、火山碎屑为主的砂砾岩储层,传统的双水模型并不能很好地求取含油饱和度,因此,双水模型的参数需要进行校正。
朱学娟等[14]通过实验分析,指出Waxman-Smits模型中难以得到真实地层因素(F*=1/qm*);而双水模型在高泥质地层中,通过Qv值校正可以得到真实的地层因素,因而应用效果更好。
在Elan程序中,通过大量实验对双水模型的岩石胶结指数也进行了泥质校正,其基本公式是
m*=m+k[0.258Cy+0.22(1-e-16.4 Cy)]
(11)
(12)
式中:m为纯净砂岩的岩石胶结指数;Cy为单位干岩样中的阳离子交换容量;k为经验系数,取值为1。
实际计算中,Cy值与泥质含量直接相关,每一种泥质(黏土)的Qv值均不一致,需要以其相对含量做权衡,求取Cy值的平均值。
2.3.2σNa值的改进方法
双水模型中,定义σNa为阳离子等效电导率。σNa与Waxman-Smits模型中的B值具有相同的物理意义,Waxman-Smits模型中给出了求取B值的经验公式的基本数学形式[11]; Juhasz等人在大量实验分析的基础上,得到B值的计算模型[15]。不论哪种模型都表明,σNa本身并不仅仅只与温度相关,还与地层水矿化度有一定关系。
黄布宙等[13]分析发现,双水模型在高泥质含量和低地层水矿化度的地层中适应性相对较差,计算含油饱和度比真实含油饱和度仍然偏低。在实验和理论分析的基础上,黄布宙等提出了改进方法,其中σNa值与地层水矿化度的关系模型[13]为

图5 W305井岩心分析粉砂质含量与测井解释结果对比Fig.5 Comparison of silty volume by core analysis and well logging interpretation
σNa=(0.0857t-0.143)(1-0.6 e-1.3σw)
(13)
其中:σNa为地层水电导率;t为摄氏温度。
改进后的方法,一定程度上能更好地适应不同的地层水矿化度,尤其是地层水矿化度较低时,符合率更高。
2.3.3 胶结指数的分类求取
从前面的分析中可知,储层微孔隙发育程度影响岩石胶结指数,应对微孔隙较发育的储层进行岩石胶结指数校正。
经过大量的实验和试算,并与岩心分析结果对比,认为依据粉砂质含量对储层进行分类,在分类基础上求取胶结指数,可提高饱和度解释精度。不同粉砂质含量岩石的m值如表3和图6所示。

表3 不同粉砂质含量的岩石胶结指数统计Table 3 Statistics of cementation exponent of different rocks with different silt volume
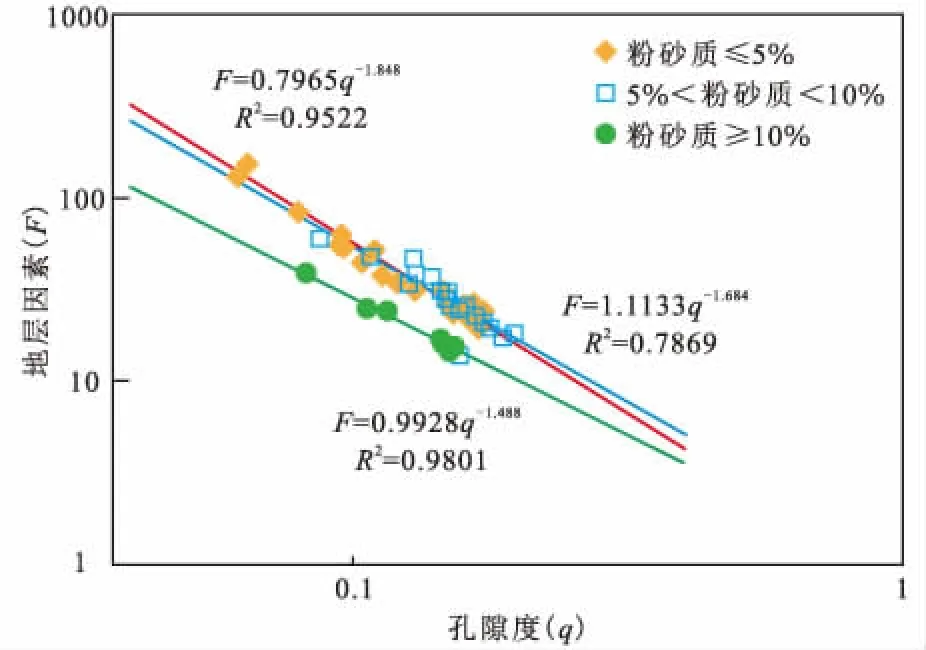
图6 不同粉砂质含量的岩石地层因素-孔隙度交汇图Fig.6 F-q cross plot of different rocks with different silt volume
3 应用效果
应用改进后的双水模型计算石南31井区含油饱和度,统计计算含油饱和度与岩心分析饱和度之间的差异表明,双水模型的计算结果与岩心分析结果更吻合,而阿尔奇公式计算结果误差偏大(表4)。
阿尔奇计算结果比双水模型平均低5.6%,在低泥质含量井段K1q11-2层2种模型计算结果一致,在高泥质含量井段K1q11-3层双水模型计算结果更接近岩心分析结果(图7)。
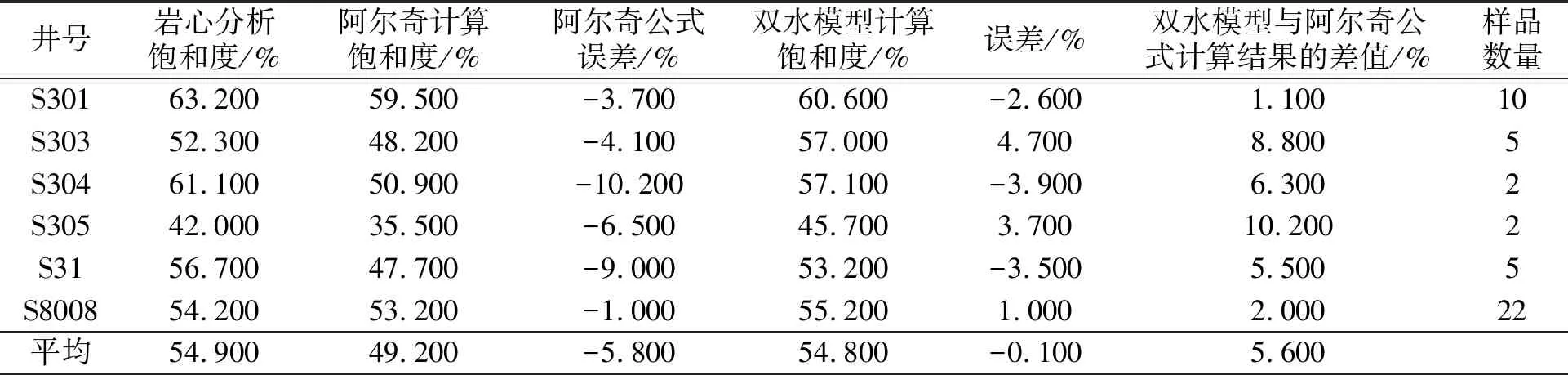
表4 双水模型与阿尔奇公式应用效果对比Table 4 Comparison of application effect of Dual-water Model with that of Archie’s Model
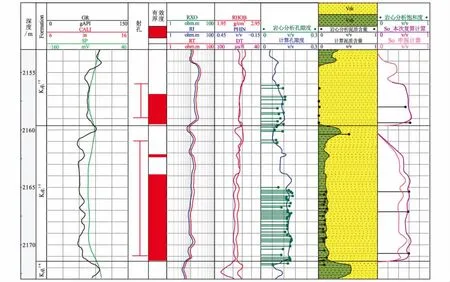
图7 双水模型解释含油饱和度与阿尔奇公式解释含油饱和度对比Fig.7 Comparison of oil saturation interpretation by Dual-water Model with that by Archie’s Model result
4 结 论
a.准确评价高泥质含量储层的含油饱和度,需要认真分析泥质含量对含油饱和度的影响;对于高岭石等附加导电性较弱的储层,仍可以使用阿尔奇公式评价含油饱和度。
b.对于微孔隙较发育的储层,不能简单地使用阿尔奇公式评价含油饱和度;在资料最不利的情况下,也应当考虑对储层进行分类评价。
c.石南31井区油层低电阻率的主要原因是微孔隙发育和泥质含量高。
d.粉砂质碎屑含量高,是储层微孔隙发育的主要原因之一。
e.新疆油田大部分区块沉积地层都以火山岩碎屑为主,由于火山岩碎屑具有较高的伽马值,泥质含量的计算方法不能简单地使用伽马等单条测井曲线计算,应认真研究泥质含量的计算方法。
f.本文提出使用粒度分析数据控制的岩性体积含量反演方法求取泥质含量和粉砂质含量,具有较高的准确度。
g.双水模型中的胶结指数m可以通过Qv值进行泥质校正,σNa值按照黄布宙等的研究成果进行校正,校正后,使用双水模型计算储层含油饱和度,与岩心分析的含油饱和度符合率较高。
h.对微孔隙引起的胶结指数变化,可以通过粉砂质含量对储层进行分类,然后再按照分类求取胶结指数,并逐类使用双水模型计算含油饱和度。

