采煤机行走轮齿形角对啮合平稳性的影响分析

史春祥

(天地科技股份有限公司 上海分公司， 上海 200030)

0 引言

采煤机以导向滑靴约束行走轮与刮板输送机销排之间的相对位置。在使用过程中，由于导向滑靴本身设计间隙，导向面的不断磨损，销排与销排之间距离的变化，销排随底板的起伏等原因，行走轮与销排的啮合中心距也在不断变化。中心距的不断变化造成速度突变，使齿面受到频繁冲击，加速齿面磨损，影响行走轮的使用寿命[1-3]。本文从行走轮齿廓曲线变换角度，通过模拟仿真的方式研究行走轮与销排在不同中心距下的啮合特性，以减小速度突变，提高行走轮啮合平稳性。

1 仿真模型的建立

建立行走轮与刮板输送机销排的啮合仿真模型，需要确定刮板输送机销排模型和行走轮模型。目前，147 mm及以上节距销排应用普遍，对应的行走轮采用渐开线齿形,一般采用20°齿形角。本文以147 mm节距为切入点，建立销排、行走轮以及两者啮合的三维仿真模型。

1.1 销排齿形

147 mm节距销排齿顶为单一较小圆弧，两侧为较大圆弧，齿廓下端与竖直方向以15°斜线与圆弧相切，见图1。

1.2 行走轮齿廓模型[4-5]

行走轮仿真模型，除采用标准20°渐开线齿形角外，还采用改变渐开线齿形角和齿廓曲线变换的方法得到4种新的齿廓曲线，最终共以5种齿形进行仿真对比。

1.2.1 齿形角改变

渐开线齿形角的大小是影响轮齿强度的重要因素，同时也是影响啮合平稳性的重要因素。分别以相对于标准20°齿形角减小2.5°和加大2.5°，即17.5°和22.5°齿形角的渐开线曲线建立仿真模型。图2为标准渐开线Ⅰ与新齿廓曲线的相对位置关系，齿廓曲线相对位置见图2中曲线Ⅱ、Ⅲ。

1.2.2 渐开线齿廓变换

与20°标准渐开线曲线齿廓相比，轮齿在分度圆处齿厚不变，以标准渐开线曲线与分度圆交点为基点，分别将原有齿廓线顺时针旋转2.5°和逆时针旋转2.5°的方式得到新的轮廓曲线。齿廓曲线相对位置如图2中Ⅳ、Ⅴ所示。

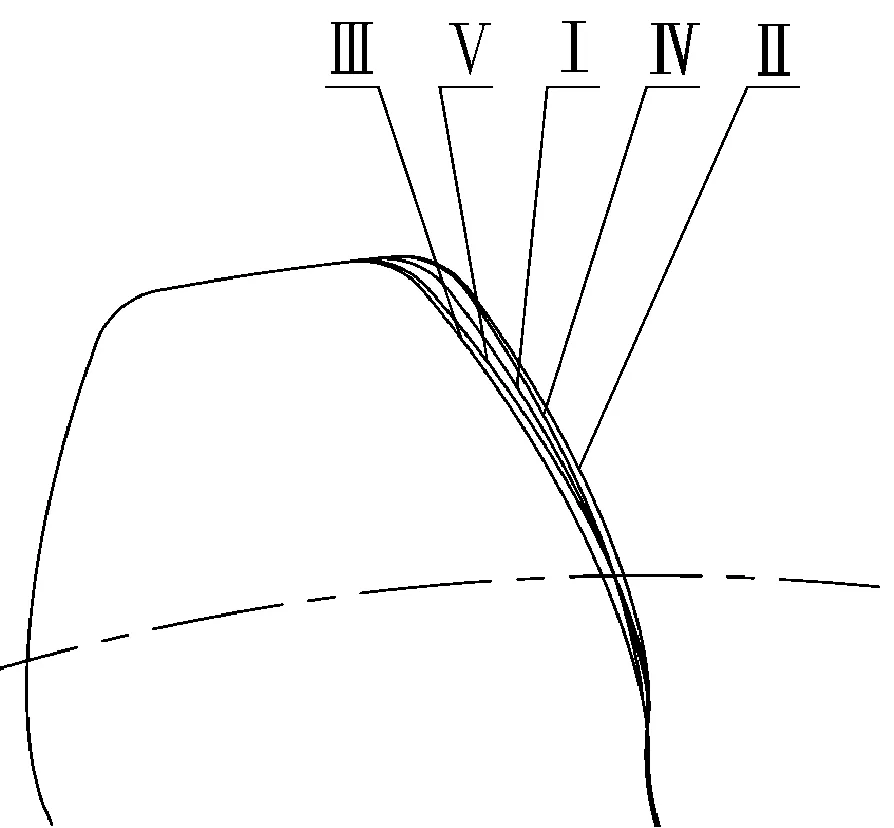
图2 5种齿形曲线相对位置图

1.3 啮合模型

运用Solid Edge建立输送机销排和5种轮廓曲线行走轮的三维模型。每个模型中，行走轮与销排之间为相对齿面啮合，设定每个啮合模型中两者之间的啮合中心距不变。如图3所示为两者三维啮合模型。

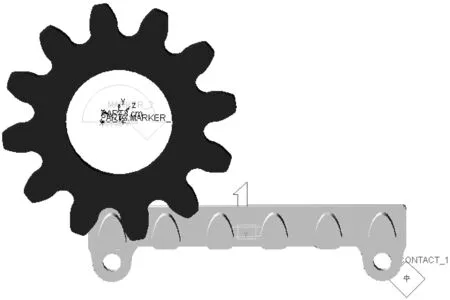
图3 行走轮与销排三维啮合模型图

2 啮合模型仿真

三维啮合模型建立后，运用Adams软件分别模拟行走轮与销排在标准中心距、中心距加大10 mm和减小5 mm三种情况下的啮合情况，对比各个啮合瞬间5种齿形在啮合点速度的变化情况。为方便操作，在仿真中将行走轮固定在中心点，以固定的转速旋转，销排则根据与行走轮齿面啮合的约束，作水平方向的直线移动，销排的运动速度即为行走轮的瞬间啮合速度。

当啮合中心距为标准中心距时，标准20°齿形角的行走轮与销排啮合速度曲线如图4所示。

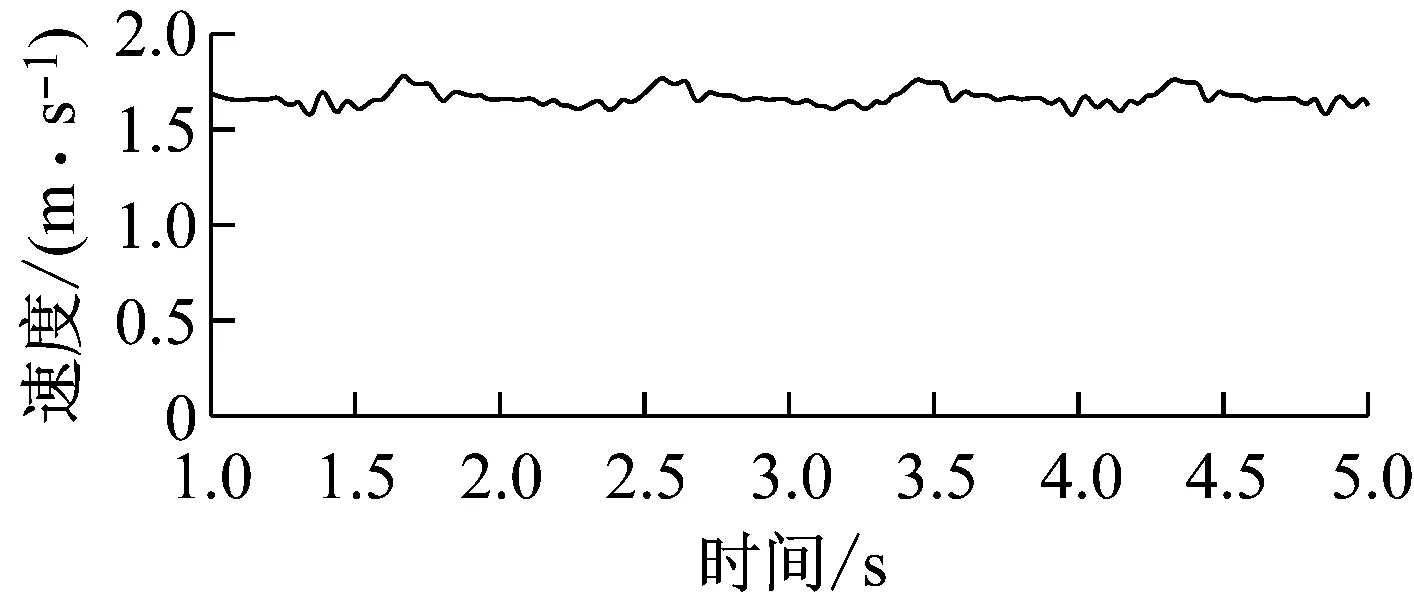
图4 20°齿形角时啮合速度曲线(标准中心距)

在此条件下，整节销排的啮合仿真过程中，销排水平方向最小速度vmin为0.156 5 m/s，最大速度vmax为0.177 7 m/s，平均速度vavg为0.166 1 m/s。

以相同的方式进行标准中心距时的仿真，得到另外4种齿形销排的速度曲线。统计5种齿形的销排速度如表1所示。其中，以绝对幅值最小的速度作为0点，其余速度值与其作对比，计算出相对幅值。

表1 标准中心距时的仿真速度

以同样的方法，可以分别得到中心距加大10 mm和减小5 mm两种情况下每种轮廓曲线的速度曲线与数据，速度统计分别如表2、表3所示。

3 仿真结果分析

从图4及表1可以看出，第Ⅳ种曲线最为平稳，其次为曲线Ⅱ，曲线Ⅰ和曲线Ⅲ相近，曲线Ⅴ最差。从表2、表3可以得出和上述基本一致的结论： 20°齿形角的标准渐开线顺时针旋转2.5°后的齿形啮合最平稳；齿形角较小的17.5°的曲线Ⅱ次之；曲线Ⅰ和曲线Ⅲ平稳性相当；曲线Ⅴ平稳性最差。

表2 中心距增加10 mm时的仿真速度

表3 中心距减小5 mm时的仿真速度

采用不同的曲线或曲线组合，通过不同中心距情况下的运动仿真，得出一致的结论：当齿形角相对较小，同时更接近销排的齿形角时，啮合相对更加平稳，速度突变更小；当齿形角增大时，速度突变幅值加大，运动冲击加剧。

4 结论

通过建立三维模型和仿真分析可知,以适当的方法减小齿形角可以提高啮合平稳性。通过在MG550/1380-WD型采煤机上的实践证实，齿形角相对较小时，啮合更平稳，有效地减少了行走轮轮齿磨损、断裂等故障，提高了齿轮使用可靠性和使用寿命。同时，由于齿形角的减小，增大了牵引力的水平分量，即牵引力的水平输出，因此提高了牵引功率的有效利用。