未知海流干扰下自主水下航行器位置跟踪控制策略研究

王金强， 王聪， 魏英杰， 张成举

(哈尔滨工业大学 航天学院， 黑龙江 哈尔滨 150001)

0 引言

自主水下航行器(AUV)是一种新型水下机器人[1]，具有体积小、灵活性好、续航能力强等显著优点，目前已广泛应用于海洋资源开发、水文观测、水下救援等领域，创造了巨大的社会和经济价值[2]。在以上AUV的实际应用中，实现对位置的精确跟踪控制是十分必要的，但由于AUV工作环境十分恶劣，易受到外界海浪和海流的干扰，很难获得精确的水动力系数，是强非线性系统。此外，AUV大多为欠驱动系统，其横向和垂向一般没有足够的控制力，这使得AUV的位置跟踪控制成为一个极具挑战性的难题。

贾鹤鸣等[3]将反步法与自适应算法相结合，提出一种针对于无外界海流干扰的欠驱动AUV自适应位置跟踪策略，并取得良好效果。段海庆等[4]将反步法与神经网络相结合，提出一种针对于水面船舶的位置跟踪算法，并通过数值仿真验证了算法的有效性。文献[5-6]设计一种反步滑模控制器，并对AUV平移速度仅对地可测时的位置进行跟踪控制，同时设计海流观测器分别对恒定和缓慢时变海流进行估计，并进行了仿真实验，验证了控制策略的有效性。Liang等[7-8]针对存在恒定海流干扰的位置跟踪控制问题，提出一种模糊反演滑模控制算法，利用自适应模糊系统对AUV系统内的非线性和不确定部分进行估计和补偿，并通过数值仿真，验证控制器的有效性和鲁棒性。周佳加等[9]提出一种改进规则自适应神经网络控制策略，并应用到AUV的速度和位置跟踪上，通过仿真实验证明了算法的有效性。王宏健等[10]将滤波反步法分别应用到欠驱动AUV的水平面和空间三维位置跟踪上，验证了控制策略的有效性，取得较好的进展。上述研究成果中的控制策略虽然均具有良好的有效性，但大多针对于AUV离海底较近，其移动速度对地可测的情况，而对于其远离海底的情况研究较少。

基于上述分析，本文针对具有参数不确定性且移动速度仅对周围水可测条件下的欠驱动AUV，设计一种位置跟踪控制策略，并通过数值仿真验证其有效性，所得结论可为AUV位置跟踪控制器的设计提供参考。

1 控制理论与AUV模型

1.1 反步法与模糊控制

反步法是一种非常有效的非线性控制器设计方法，其是将整个系统分解为多个不超过系统最高阶数的子系统，而后针对每个子系统基于李雅普诺夫定理设计虚拟控制量和控制函数，最终保证整个非线性系统的稳定性。

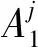
(1)

式中：θ=(θ1,θ2,…,θj,…,θk)T为系统自适应参数向量，θj为模糊系统自适应参数；ξ为模糊基向量；ξj(x)为模糊函数，

(2)

1.2 AUV数学模型

本文所针对的欠驱动AUV是一种具有飞翼式对称外形的新型AUV，其重心和浮心位于同一铅垂线上，并忽略其横滚角及角速度，且与传统AUV相比具有更加优良的综合水动力性能和经济性能[12]，结构如图1所示。

图1 AUV结构布置图Fig.1 Structural arrangement of the autonomous underwater vehicle

根据欠驱动AUV的运动特性，则其在海流干扰下的水平面运动学方程为

(3)

动力学方程表示为

(4)

式中：vcx、vcy分别为海流在惯性系下的速度；x、y为惯性系下AUV的水平面位置坐标；ur、vr分别为体坐标系下其相对于周围水的纵向和横向速度；ψ、r分别为艏向角和角速度；τu、τr分别为AUV尾部螺旋桨推力和尾部舵翼产生的力矩；mii为AUV质量和附加质量的合并项，i=1,2,3；m为AUV质量；Iz为AUV纵平面转动惯量；X(·)、Y(·)、N(·)为AUV黏性流体水动力系数，具体含义请参考文献[6]，此处不再详细说明。由于实际工程中AUV具有参数不确定性，故本文假设(4)式中的mii的标称值不够精确，以m、mo和mp分别代表其实际值、标称值和摄动值，并满足：

(5)

式中：λ为未知常数，且满足-0.5<λ<0.

此外本文同时假设AUV黏性水动力系数完全未知，为方便表述，定义：

(6)

式中：χ1、χ2、χ3为未知恒定矢量；κ1、κ2、κ3为速度矢量。则(4)式可重写为

(7)

xe=xd-x，ye=yd-y，

(8)

则体坐标系下位置跟踪误差εx和εy可定义为

(9)

由(9)式可以看出，当εx和εy的值趋近于0时，xe和ye同样趋近于0，则只需设计控制律使εx和εy快速收敛到0附近一个任意小的邻域，根据(3)式和(9)式，计算可得εx和εy的导数为

(10)

2 位置跟踪控制器设计

2.1 控制器设计

本节基于李雅普诺夫理论和反步法，共分6个步骤对欠驱动AUV的位置跟踪控制器进行设计：

1)稳定位置跟踪误差εx和εy.

首先定义李雅普诺夫控制函数为

(11)

其导数为

(12)

定义变量：

ϑ=ρsinψe，

(13)

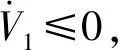
(14)

式中：σ1、σ2均为待定的正常数；cx、cy为海流观测器对vcx和vcy的估计值，并定义：

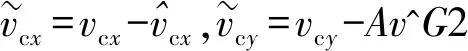
(15)

将(14)式和(15)式代入(12)式中，可得

(16)

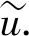
考虑到ud和ϑd为虚拟的控制输入，定义：

(17)

则(16)式变为

(18)

定义一个新的李雅普诺夫函数V2为

(19)

则其导数变为

(20)

结合(7)式和(20)式选取控制输入τu为

(21)

式中：σ3、δ1均为未知待定正常数。为减弱切换增益过大导致的系统抖振，本文采用模糊系统逼近则(20)式可变换为

(22)

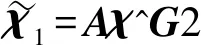
(23)

自适应律为

(24)

式中：β1为未知正常数。

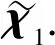
重新定义一个李雅普诺夫函数为

(25)

式中：γ1为未知正常数。则V3的导数为

(26)

选取自适应律为

(27)

(28)

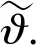
首先定义一个新的李雅普诺夫函数V4为

(29)

结合(14)式和(28)式，其导数可表示为

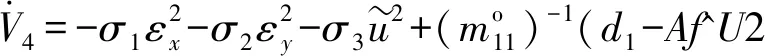
(30)

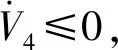
(31)

式中：σ4为一个待定的未知正常数。将rd代入到(30)式中，可得

(32)

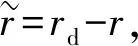
物联网智能节点通过无线自组织网络实现指令的下发和数据的接收处理，与底层模块之间的数据传输基于Modbus协议，采用主从通信方式，系统采用Modbus协议中传输效率高的RTU模式传送数据，数据包分为地址码，功能码，数据位，校验码4部分，每个底层模块具有一个字节长度的唯一地址码[12]，智能节点下发至检测模块数据包中功能码为0x03，功能为读保持寄存器，数据位为读寄存器的地址和数量，读取传感器采集的环境参数。智能节点下发至控制模块数据包中功能码为0x06，功能为写单个寄存器，数据位为写入寄存器的地址和写入寄存器的值，对设备进行控制。RTU模式下采用CRC校验方式。

(33)

则其导数为

(34)

选取控制输入为

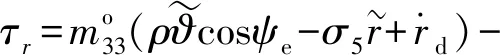
(35)

式中：σ5、δ3均为未知待定正常数。为减弱控制器抖振，采用模糊系统逼近则(34)式可变换为

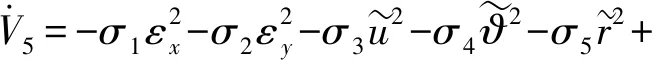
(36)

(37)

自适应律为

(38)

式中：β3为未知正常数。

(39)

则其导数为

(40)

选择自适应律为

(41)

则(40)式变为

(42)

2.2 观测器设计

本节主要设计一个针对于缓慢未知时变海流的观测器，使其估计值cx、cy收敛于未知海流速度vcx和vcy，则根据(4)式可得

(43)

若选择:

(44)

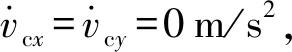
(45)

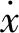
(46)

同理，若选择：

(47)

则最终有

(48)

2.3 稳定性证明

(49)

则其导数为

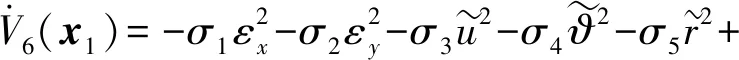
(50)

模糊系统最优参数选为

(51)

式中：Ωu、Ωr分别为u、r的集合。则(50)式可变换为

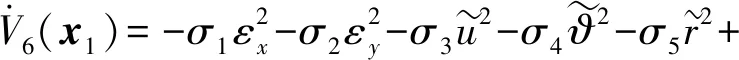
(52)

(53)

则其导数变为

(54)

(55)

则子系统Σ1是全局一致渐进稳定的，而对于子系统Σ2首先定义一个新的李雅普诺夫函数Vc为

(56)

其导数为

(57)

则子系统Σ2也是全局一致稳定，故整个欠驱动AUV闭环系统也是稳定的。

3 AUV位置跟踪仿真

为更好地验证AUV位置跟踪控制器的跟踪效果，本节所有数值仿真中均采用相同控制器参数，具体如下：σ1=12，σ2=6，σ3=σ4=1，σ5=0.6，γ1=γ3=0.02，α1=α2=0.1，β1=80，β2=30，自适应模糊系统中，向量u、r的初始值均设为0，系统隶属函数取为

(58)

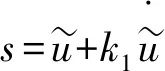
(59)

为更加全面地验证控制器性能，本文选取以下两个期望轨迹，分别为：

1) 圆轨迹

(60)

2) 正弦轨迹

(61)

结合AUV实际工程应用，本文假设其纵向推力始终为正，且控制输入的幅值及其变化率均受限，具体为

(62)

此外为验证控制器鲁棒性，本文假设AUV质量和附加质量均具有最大25%的相对不确定性，选取以下3个仿真模型，分别为：1)采用标称参数的模型1；2)采用mp=-0.25mo不确定参数的模型2；3)采用mp=0.25mo不确定参数的模型3. 总仿真时间1 500 s，仿真结果如图2和图3所示。

图2 圆轨迹位置跟踪仿真结果Fig.2 Simulated results of position tracking of circular trajectories

图3 正弦轨迹位置跟踪仿真结果Fig.3 Simulated results of position tracking of sinusoidal trajectories

4 结论

本文针对平移速度仅对周围流体可测，且具有参数不确定性和外界未知海流干扰的欠驱动AUV位置跟踪控制问题，基于反步法和自适应控制技术提出一种非线性鲁棒控制策略，并采用模糊控制算法对控制器中的鲁棒项进行优化，提高了系统的鲁棒性，同时设计了针对外界未知时变海流的干扰观测器，并利用李雅普诺夫理论证明了整个闭环系统的稳定性，最终通过数值仿真证明了所提出控制策略的有效性和鲁棒性。下一步，将搭建试验平台，利用试验方法验证本文位置跟踪控制算法的有效性。