考虑跨数影响的单线铁路简支梁桥桥墩地震响应
鲜国,魏标,李传富,王祯伟,杜雪松
考虑跨数影响的单线铁路简支梁桥桥墩地震响应
鲜国1,魏标2,李传富1,王祯伟3,杜雪松2
(1.成兰铁路有限责任公司,四川 成都 610032; 2. 中南大学 土木工程学院,湖南 长沙 410075; 3. 浙江省交通规划设计研究院,浙江 杭州 310006)
针对8 m和25 m2种墩高的单线铁路简支梁桥,研究跨数对中间桥墩地震响应的影响程度。采用OpenSEES程序,分别建立2跨,4跨,6跨和8跨共4种不同跨数的桥梁有限元模型。通过不同方向、不同烈度的地震动作用下地震响应的对比分析,确定跨数对中间桥墩地震响应的影响程度。研究结果表明:在纵向地震动作用下,中间桥墩地震响应随跨数的增加而增加,并在跨数多于4跨时增加趋势变缓;在横向地震动作用下,中间桥墩地震响应随跨数的增加而先增加后减小,并在跨数为4跨时达到最大值。以上趋势随着墩高和地震烈度的增加而减小,但在桥墩屈服前后略有波动。因此,在进行单线铁路简支梁桥的普通高度桥墩地震响应分析时,为了同时提高计算精度和计算效率,建模跨数以4跨为宜。
单线铁路;简支梁桥;跨数;墩高;地震响应
铁路简支梁桥是我国高速铁路的重要组成部分,对于多跨铁路简支梁桥,相邻结构与边界条件对其抗震性能的影响不能忽视[1−2]。早期的多跨铁路桥梁设计,往往仅限于主桥,并着眼于纵向地震反应的分析[3]。但过去的地震和研究表明,多跨简支梁桥邻梁间较容易受到地震损伤,容易引起耦合响应[4−5]。马青青[6]认为,若采用未考虑梁跨间耦联效应的单跨模型,可能会低估邻梁间碰撞和落梁风险;此外,高玉峰[7]也认为对多跨简支梁桥进行横向地震动分析时,应考虑相邻联结构的耦合响应,否则计算结果有可能偏于不安全。因此,在进行桥梁建模时应采用更详细的建模方法,并多建几跨作为边界条件,以正确反映桥梁结构的地震响应[8]。另一方面,在建模计算过程中既要考虑计算精度,也应考虑计算时间。虽然在条件允许时,多建几跨桥梁作为边界条件能够获得更准确的数据[9],但随着建模跨数的增加,桥梁模型变得复杂,计算时间将延长[10]。Simon等[11]认为在多跨桥梁地震分析中应该选用合适的数值模型以提高计算效率;同时MA等[12]也认为用跨数较少的模型代替跨数较多的模型可以节约计算时间,提高计算效率。所以在能够保证一定计算精度的条件下,应尽可能少取简支梁跨数。尤其对于相应的振动台试验,限于目前振动台的承载能力,更需要合理平衡试验精度和效率的关系。《城市桥梁抗震设计规范》[13]规定在桥梁抗震计算中应两边各取一联作为边界条件。本文在此基础上探究在不同地震方向和不同地震烈度条件下跨数对典型单线铁路简支梁桥的地震反应。以成兰铁路区间的单线简支梁桥为例,利用Open SEES有限元软件开展非线性地震时程分析,研究了在不同地震方向和不同地震烈度的条件下4种不同跨数的简支梁桥中间桥墩的地震反应,并选择出一个较为合适的建模跨数,为单线铁路简支梁桥的建模分析和振动台试验提供技术参考。
1 计算模型
1.1 主梁
成兰铁路单线简支梁桥主梁采用有砟轨道预制后张法两片式预应力混凝土T型截面,两片T梁之间采用桥面板及横隔板联成整体,并在横隔板处施加横向预应力,如图1所示。每跨主梁计算跨度为32 m,采用C55混凝土,梁高2.7 m。每片T梁顶板宽为2.28 m,下缘宽为0.88 m,截面面积2.92 m2。

单位:mm
1.2 桥墩
由于该地区地形起伏较大,本文分别采用8 m和25 m2种墩高进行分析,墩身采用C35混凝土。8 m高桥墩(代表矮墩)采用等截面实体墩,如图2所示。25 m高桥墩(代表中高墩)采用变截面实体墩,如图3所示。

单位:mm
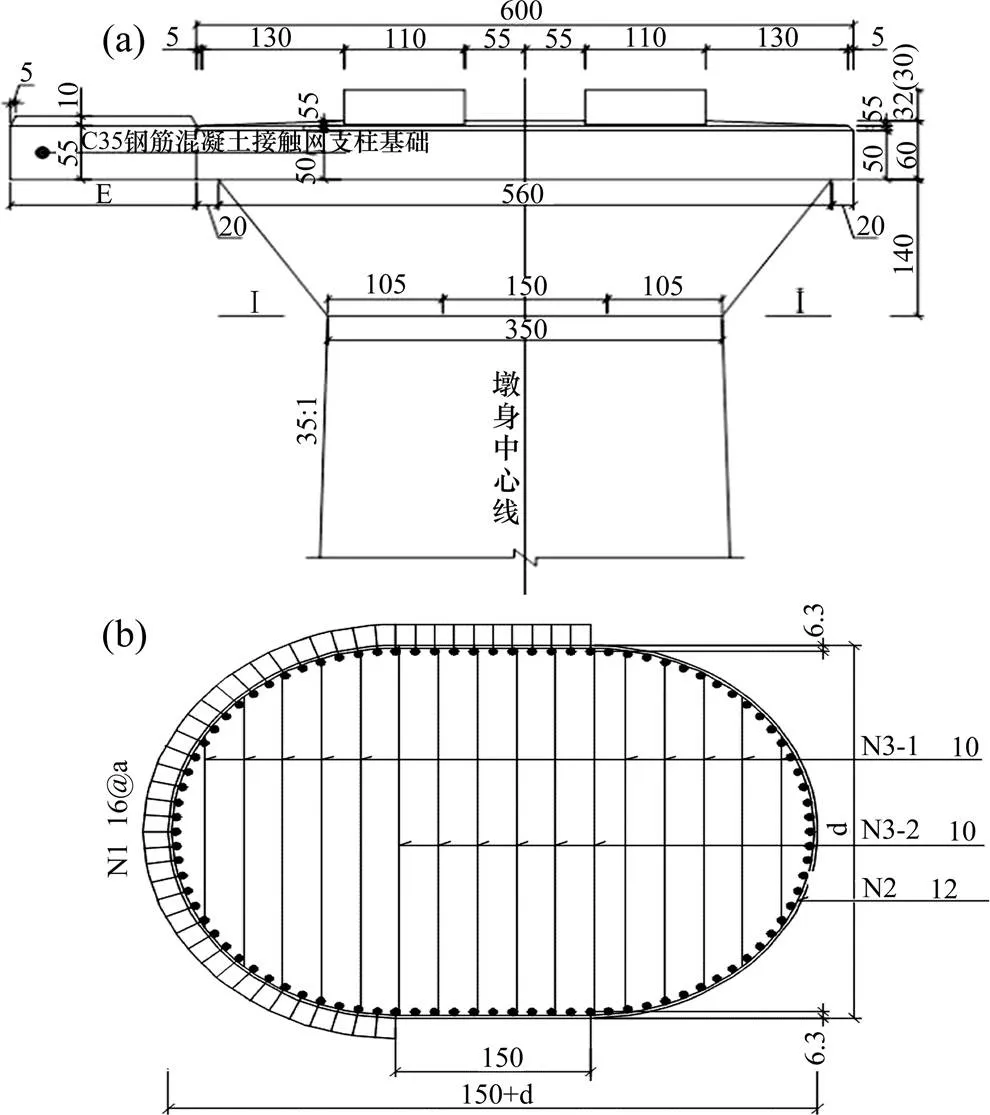
单位:mm
1.3 有限元模型
为研究简支梁跨数的变化对中间桥墩地震响应的影响,保持原跨径、墩高和截面尺寸等不变[14],分别建立了2跨,4跨,6跨以及8跨简支梁桥模型,如图4所示。

图4 中墩的不同边界条件
采用有限元软件OpenSEES建立三维有限元模型,分别对桥梁的上部结构、支座、桥墩等主要部件进行模拟,墩底边界条件为墩底固结。其中,8 m墩高和25 m墩高的2跨简支梁桥模型,如图5 所示。
每跨主梁两端分别放置2个固定球型支座KZQZ3000GD和2个纵向滑动球型支座KZQZ3000 ZX,即每墩墩顶有4个支座,如图6所示。
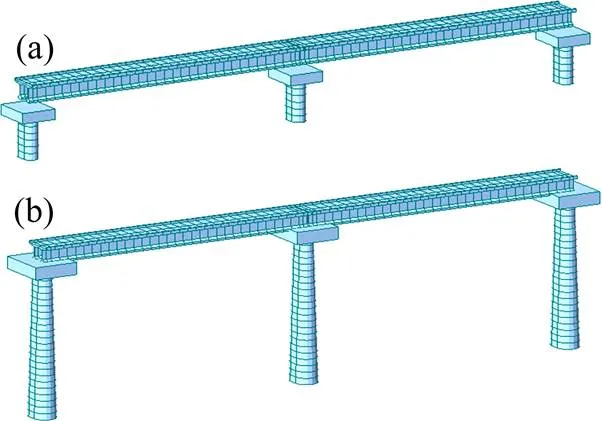
(a) 8 m墩高模型;(b) 25 m墩高模型

(a) 支座布置图;(b) 连接示意图
2 地震动输入
根据安评报告[15],采用3个不同等级(分别为100 a超越概率63%,50 a超越概率10%和100 a超越概率10%)的地震动输入,对应的反应谱曲线如图7所示。每个等级的反应谱对应21条地震波,其中,虚线表示每条地震波的反应谱,实线表示其平均谱。对桥梁有限元模型分别进行纵向地震动输入和横向地震动输入,开展非线性时程分析。

(a) 100 a超越概率63%;(b) 50 a超越概率10%;(c) 100 a超越概率10%
3 地震反应
3.1 误差定义
为便于分析,引入平均误差的概念。墩底弯矩和墩顶位移平均误差分别定义为:
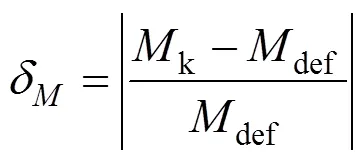

式(1)和(2)中:k和k分别为某跨数的简支梁桥模型中墩的墩底弯矩和墩顶位移;为了同时提高计算精度和计算效率,暂以4跨简支梁桥的地震响应为基数进行分析,def和def分别为4跨简支梁桥模型中墩的墩底弯矩和墩顶位移。
3.2 纵向地震作用
图8列出了100 a超越概率63%的纵向地震动输入下的中墩墩底纵向弯矩反应及墩顶纵向位移反应,这些中墩地震反应随着简支梁跨数的增加而逐渐增大。在跨数从2跨增加到4跨时最为显著:相对于4跨简支梁桥,8 m墩高2跨简支梁模型中墩墩底弯矩和墩顶位移的平均误差分别为13.3%和29.6%;25 m墩高2跨简支梁模型中墩墩底弯矩和墩顶位移的平均误差分别为6.3%和13.2%。相对于4跨简支梁桥,随着跨数的继续增加,中墩墩底弯矩和墩顶位移增加趋势变缓,平均误差在10%以内。上述趋势是因为纵向滑动支座并没有完全释放主梁与桥墩的纵向约束,跨数越多导致中墩承受的惯性力越大。

(a) 8 m中墩墩底弯矩;(b) 25 m中墩墩底弯矩;(c) 8 m中墩墩顶位移;(d) 25 m中墩墩顶位移

(a) 50 a超越概率10%地震对应弯矩;(b) 50 a超越概率10%地震对应位移; (c) 100 a超越概率10%地震对应弯矩;(d) 100 a超越概率10%地震对应位移
图9为50 a10%和100 a10%超越概率的纵向地震动输入下的中墩墩底纵向弯矩反应及墩顶纵向位移反应。随着简支梁跨数的增加,中墩地震反应的变化趋势与图8类似。对比图8和图9,随着地震超越概率从100 a63%变化为50 a10%和100 a10%,2跨简支梁桥模型的中墩墩底弯矩平均误差分别为13.3%,1.7%和1.2%,墩顶位移平均误差分别为29.8%,2.2%和0.7%;8跨简支梁桥模型的中墩墩底弯矩平均误差分别为3.0%,0.3%和0.0%,墩顶位移平均误差分别为7.5%,0.2%和0.1%。以上数据表明,随着地震强度的增大,中墩地震反应误差变小。上述趋势是因为随着地震强度的增大,纵向滑动支座的相对约束作用减弱,同时中墩逐渐进入损伤、屈服(桥墩在地震超越概率50 a10%附近时开始屈服)等非线性状态,将更多的惯性力转移给其他桥墩,因此,中墩地震反应受跨数的影响变小。
3.3 横向地震作用
图10为100 a超越概率63%的横向地震动输入下的中墩墩底横向弯矩反应及墩顶横向位移反应,这些中墩地震反应随着简支梁跨数的增加而先增大后减小,并在跨数为4时达到最大值。相对于4跨简支梁桥,8 m墩高2跨简支梁模型中墩墩底弯矩和墩顶位移的平均误差分别为2.7%和8.2%;25 m墩高2跨简支梁模型中墩墩底弯矩和墩顶位移的平均误差分别为3.1%和8.1%。上述趋势是因为支座在横桥向对主梁与桥墩进行了约束,跨数由2变为4将导致中墩承受的惯性力变大。但随着跨数的继续增加,中墩扭转振型日益显著,并且扭转振型周期越来越趋向于横向振型周期,处于桥梁几何中心的中墩内力减小。
图11为50 a10%和100a10%超越概率的横向地震动输入下的中墩墩底横向弯矩反应及墩顶横向位移反应。随着简支梁跨数的增加,中墩地震反应的变化趋势与图10类似。对比图10和图11,随着地震超越概率从100a 63%变化为50 a10%和100 a10%,2跨简支梁桥模型的中墩墩底弯矩平均误差分别为2.7%,2.1%和0.5%,墩顶位移平均误差分别为8.2%,5.9%和3.0%;8跨简支梁桥模型的中墩墩底弯矩平均误差分别为6.7%,8.9%和4.1%,墩顶位移平均误差分别为17.7%,21.5%和13.4%。以上数据表明,随着地震强度的增大,中墩地震反应误差变小。上述趋势是因为随着地震强度的增大,中墩逐渐进入损伤、屈服(桥墩一般在地震超越概率50 a10%附近时开始屈服)等非线性状态,将更多的惯性力转移给其他桥墩,总体上,中墩地震反应受跨数的影响变小。但对于50 a10%和100 a10%超越概率的横向地震输入,4跨简支梁模型中墩墩底进入屈服状态,而8跨简支梁模型由于横向振型与扭转振型耦合导致中墩墩底没有屈服,因此,平均误差稍有增加;当地震强度增加到100 a超越概率10%时,不同跨数模型的中墩墩底全部进入屈服状态,平均误差减小。

(a) 8 m中墩墩底弯矩;(b) 25 m中墩墩底弯矩; (c) 8 m中墩墩顶位移;(d) 25 m中墩墩顶位移
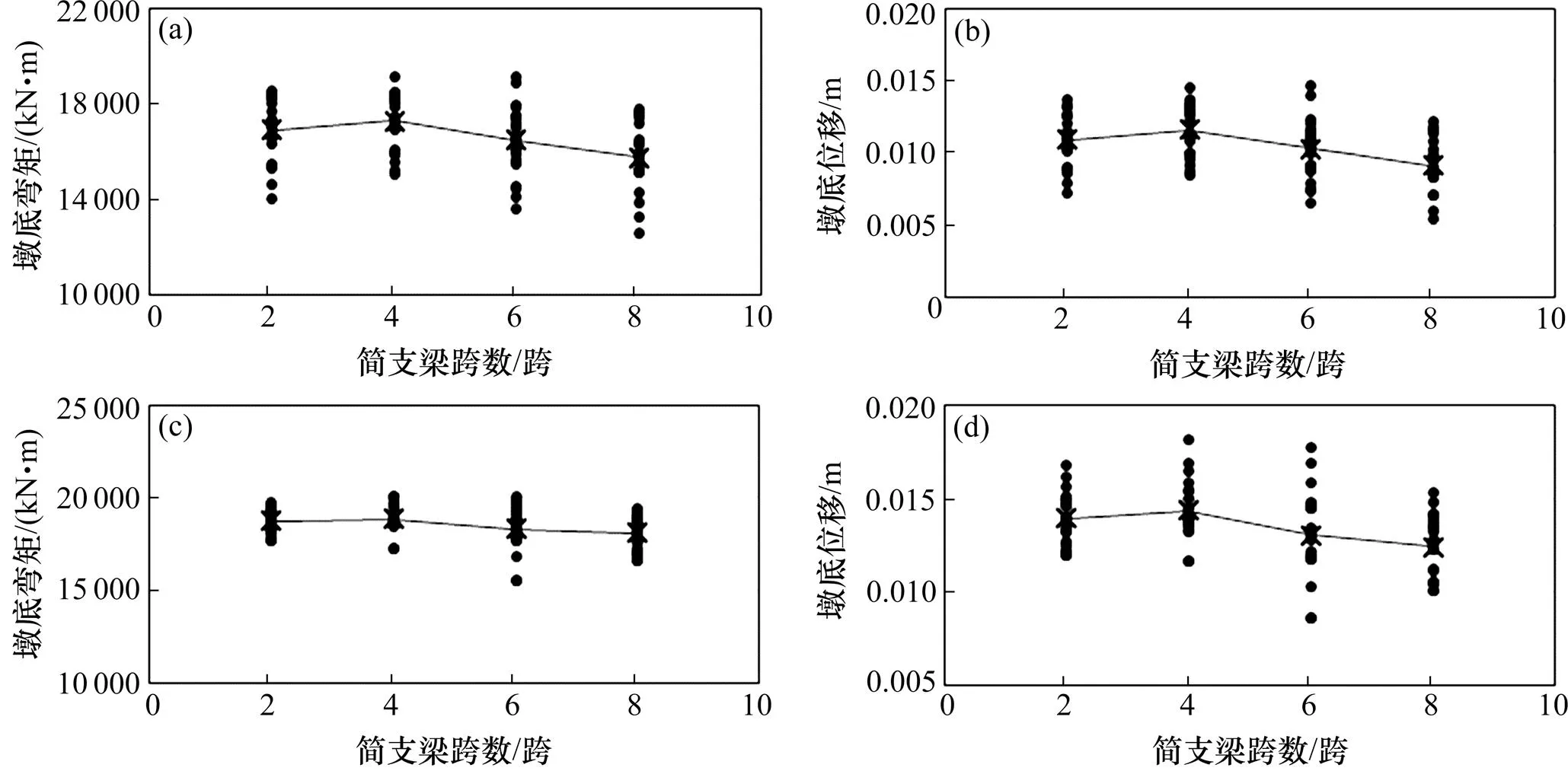
(a) 50 a超越概率10%地震对应弯矩;(b) 50 a 超越概率10%地震对应位移; (c) 100 a超越概率10%地震对应弯矩;(d) 100 a超越概率10%地震对应位移
4 结论
1) 纵桥向地震输入时,由于相邻跨的纵向耦合振动,中墩的地震响应随跨数的增加而增加,并在跨数多于4跨时增加变缓;横桥向地震输入时,由于相邻跨横向耦合振动和桥梁横向振动与扭转振动变化等原因,中墩的地震响应随跨数增加而先增加后减小,并在跨数为4跨时达到最大值。
2) 对于普通高度的桥墩(包括矮墩和中高墩),结论(1)中的变化趋势随着墩高的增加而减小,同时随着地震烈度的增加而减小。对于后者,在一定地震烈度下,由于不同跨数引起的桥梁横向振动与扭转振动变化等原因,导致不同跨数的中墩屈服时刻不同,将略微影响上述变化趋势。当地震烈度继续增加时,不同跨数的中墩都屈服,且中墩地震反应之间的误差继续减小。
3) 纵桥向地震输入时,4跨简支梁模型误差可以控制在20%以内;横桥向地震输入时,4跨简支梁模型的地震响应比其他跨数的模型大。因此,在进行典型单线铁路简支梁桥的桥墩地震响应分析时,为了同时提高计算精度和计算效率,建模跨数以4跨为宜。
[1] DAI G, YAN B. Seismic pounding and protection measures of simply-supported beams considering interaction between continuously welded rail and bridge[J]. Structural Engineering International, 2013, 23(1): 61−67.
[2] 康圣雨. 大跨度连续刚构与多跨简支梁引桥在地震作用下的碰撞效应研究[D]. 成都: 西南交通大学, 2016. KANG Shengyu. Research on the collision effect under seismic response between the long-span continuous rigid frame bridge and the multi-span simply supposed bridge[D]. Chengdu: Southwest Jiaotong University, 2016.
[3] 蒋娜芳, 魏斌, 谢斌. 大跨度桥梁主引桥横向耦合地震效应研究[J]. 结构工程师, 2009, 25(5): 71−75. JIANG Nafang, WEI Bin, XIE Bin. Study on seismic transverse coupling interactive effect of large span bridges with approach bridges[J]. Structural Engineers, 2009, 25(5): 71−75.
[4] Won J H, Mha H S, Kim S H. Effects of the earthquake-induced pounding upon pier motions in the multi-span simply supported steel girder bridge[J]. Engineering Structures, 2015(93): 1−12.
[5] Chouw N, Hao H. Significance of SSI and nonuniform near-fault ground motions in bridge response I: Effect on response with conventional expansion joint[J]. Engineering Structures, 2008, 30(1): 141−153.
[6] 马青青. 考虑基础—结构相互作用的长多跨桥的地震响应研究[D]. 北京: 北京交通大学, 2016.MA Qingqing. Study on the seismic response of bridge with large number of spans considering foundation- structure interactive[D]. Beijing: Beijing Jiaotong University, 2016.
[7] 高玉峰. 考虑碰撞效应的桥梁非线性地震反应特性研究[D]. 成都: 西南交通大学, 2010.GAO Yufeng. The nonlinear seismic response characteristics of bridge considering pounding effects[D]. Chengdu: Southwest Jiaotong University, 2010.
[8] Siqueira G H, Tavares D H, Paultre P, et al. Performance evaluation of natural rubber seismic isolators as a retrofit measure for typical multi-span concrete bridges in eastern Canada[J]. Engineering Structures, 2014, 74(74): 300− 310.
[9] 戴公连, 朱俊樸, 闫斌. 大轴重重载铁路简支梁桥梁轨相互作用研究[J]. 桥梁建设, 2014, 44(5): 27−32.DAI Gonglian, ZHU Junpu, YAN Bin. Study of beam and track interaction for simply-supposed beam bridge of heavy axle load heavy haul railway[J]. Bridge Construction, 2014, 44(5): 27−32.
[10] Naderian H, Cheung M M S, Shen Z, et al. Seismic analysis of long-span cable-stayed bridges by an integrated finite strip method[J]. Journal of Bridge Engineering, 2015, 21(3): 1−18.
[11] Simon J, Vigh L G. Seismic fragility assessment of integral precast multi-span bridges in areas of moderate seismicity[J]. Bulletin of Earthquake Engineering, 2016, 14(11): 1−26.
[12] MA Q, ZHANG H. Transfer matrix algorithm of the longitudinal seismic response of multi-span simply supported girder bridge[J]. Metallurgical & Mining Industry, 2015, 7(4): 162−166.
[13] CJJ11—2011, 城市桥梁抗震设计规范[S]. CJJ11—2011, Code for seismic design of urban bridges[S].
[14] ZHANG Y L, ZHAO J D, CHEN X C, et al. Influence of track system restraint on seismic response of high-speed railway long-span continuous girder bridge[J]. Journal of Railway Engineering Society, 2015, 32(7): 46−50.
[15] Azarbakht A, Shahri M, Mousavi M. Reliable estimation of the mean annual frequency of collapse by considering ground motion spectral shape effects[J]. Bulletin of Earthquake Engineering, 2014, 13(3): 1−21.
Effects of span number on seismic responses of simply supported bridge piers in a single line railway
XIAN Guo1, WEI Biao2, LI Chuanfu1, WANG Zhenwei3, DU Xuesong2
(1. Chengdu-Lanzhou Railway Co., Ltd, Chengdu 610032, China; 2. School of Cirvl Engineering, Central South University, Changsha 410075, China; 3. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310006, China)
Aiming at simply supported bridges, respectively with two pier heights of 8m and 25 m, in a single line railway, the effects of bridge span number on the seismic responses of middle pier were studied. The bridge span number adopted 2, 4, 6 and 8, respectively, in the OpenSEES program, and the corresponding bridge models were analyzed under earthquakes with different input directions and intensities. The seismic responses compared among different bridge models show that when the bridge span number increases, the seismic responses of middle pier increase under the longitudinal earthquakes while those firstly increase and then decrease under the transverse earthquakes. The former’s increasing trend becomes insignificant when the bridge span number is more than 4, while the latter reaches the peak value when the bridge span number adopts 4. The above rules are weakened as the pier heights and earthquake intensities increase, and irregularly changes only when the piers are yielding. It is necessary to adopt 4-span bridge to calculate the seismic responses of middle pier of simply supported bridge in a single line railway, by comprehensively considering the calculation accuracy and efficiency.
single line railway; simply supported bridge; bridge span number; pier height; seismic response
10.19713/j.cnki.43−1423/u.2019.03.018
U448.27
A
1672 − 7029(2019)03 − 0698 − 08
2018−03−29
国家自然科学基金资助项目(51778635;51778630);湖南省自然科学基金资助项目(2019JJ40386)
魏标(1982−),男,江苏徐州人,教授,博士,从事桥梁抗震领域的研究;E−mail:weibiao@csu.edu.cn
(编辑 蒋学东)

