基于有限元分析的横向受荷刚性桩应变楔模型形体参数研究

赵明华，李帅超，彭文哲



基于有限元分析的横向受荷刚性桩应变楔模型形体参数研究

赵明华，李帅超，彭文哲

(湖南大学 岩土工程研究所，湖南 长沙 410082)

为研究应变楔模型中形体参数的变化规律，以已有的砂土与黏土试验参数为依据，通过ABAQUS有限元软件对横向荷载下刚性桩的三维模型进行有限元分析。采用莫尔库仑本构模型、罚函数非连续接触算法以及线性缩减积分单元建立横向荷载下刚性桩的三维有限元模型，并对模型进行验证。根据ABAQUS的分析结果确定应变楔的边界应变值，确定应变楔的各个形体参数。基于控制变量法分析砂土与黏土中各应变楔形体参数的变化规律。对各参数进行回归分析，得到砂土与黏土中应变楔底角与长度的拟合公式。研究结果表明：不同土质下应变楔模型的形体参数在不同横向荷载、弹性模量以及内摩擦角下呈现的变化规律有明显差异，故对于不同土质下的应变楔模型宜分开进行考虑。

横向荷载；刚性桩；应变楔；有限元；影响因素

桩基础除了主要承受竖向荷载之外，还会承受一定的横向荷载，特别是在桥梁基础中所承受的交通荷载，在建筑工程中承受上部结构所传递的风荷载以及地震荷载，在港口码头所承受的系泊船只的撞击力以及拉力，在海洋平台基础所承受的水流或者波浪施加的荷载，这些横向荷载更加不容忽视。对于横向荷载作用下的桩，早在20世纪50年代就有学者开始进行研究，发展至今，对于横向荷载作用下桩的分析方法可以分为弹性地基反力法[1]、极限平衡法[2]、复合地基反力法[3]、弹性理论法[3]以及应变楔方法等。其中应变楔方法不仅能考虑不同土质下桩的内力与变形、刚度、截面形状以及桩身材料的非线性，还能考虑土体的连续性及液化，相比其他分析方法有其独特的优越性。应变楔模型由Norris等[4−5]提出，他将一维的弹性地基梁法拓展到三维领域，提出了应变楔模型；Ashour等[6−7]应用应变楔方法对层状砂土与黏土地基及岩层中的横向荷载作用下长桩和群桩进行了受力分析；李忠诚等[8]将应变楔应用于被动桩主动土压力计算，建立了被动桩桩土相互作用的整体平衡方程；Ardalan等[9]将应变楔模型用于抗滑桩的桩土相互作用分析；陈昌富等[10]将应变楔底面水平的假定修正为螺旋对数曲面；XU等[11]考虑了应力应变非线性关系对应变楔模型进行了修正；杨明辉等[12]开展了斜坡上基桩的横向加载破坏试验，提出了考虑坡度效应的土体应变楔模型。虽然应变楔方法经过数十年的发展，取得了很多成果，但是目前仍存在着许多不足之处：部分形体参数的取值采取人为假定或采用经验取值；对应变楔形体参数的变化规律以及影响因素缺少全面深入的分析。针对以上不足之处，适宜采用有限元分析来解决。已有不少学者采用有限元数值模拟对横向荷载作用下的桩身响应进行分析研究，彭芳乐等[13]基于一种考虑岩体的低抗拉强度特点的三维弹塑性有限元数值分析，对岩体斜面上设置的刚性桩基础的横向承载力进行了分析与评价，并与现场试验结果进行了比较分析；金青等[14]对刚性桩进行了有限元模拟，分析了桩的横向承载力与土体参数的变化规律；张华华[15]利用有限元软件分析了横向荷载作用下桩的桩侧土对桩身的反力、变形以及应力应变分布问题。但有限元分析中较少涉及应变楔模型。针对应变楔方法的不足，本文基于已有的应变楔理论以及ABAQUS有限元软件，通过数值模拟建立横向荷载作用下刚性桩的三维模型，并由有限元分析结果定义各应变楔形体参数，之后，对比分析砂土与黏土中不同横向荷载、土体弹性模量、土体黏聚力和土体内摩擦角下的形体参数，得出规律性的结论并且分析其影响程度，以期完善应变楔模型的理论研究。

1 应变楔基本模型

应变楔基本模型最早是由Norris[5]于1986年提出，后经过众多学者的发展逐渐完善。目前认为桩基础在承受横向荷载时，桩前会出现三维被动土楔(即应变楔)，如图1所示。

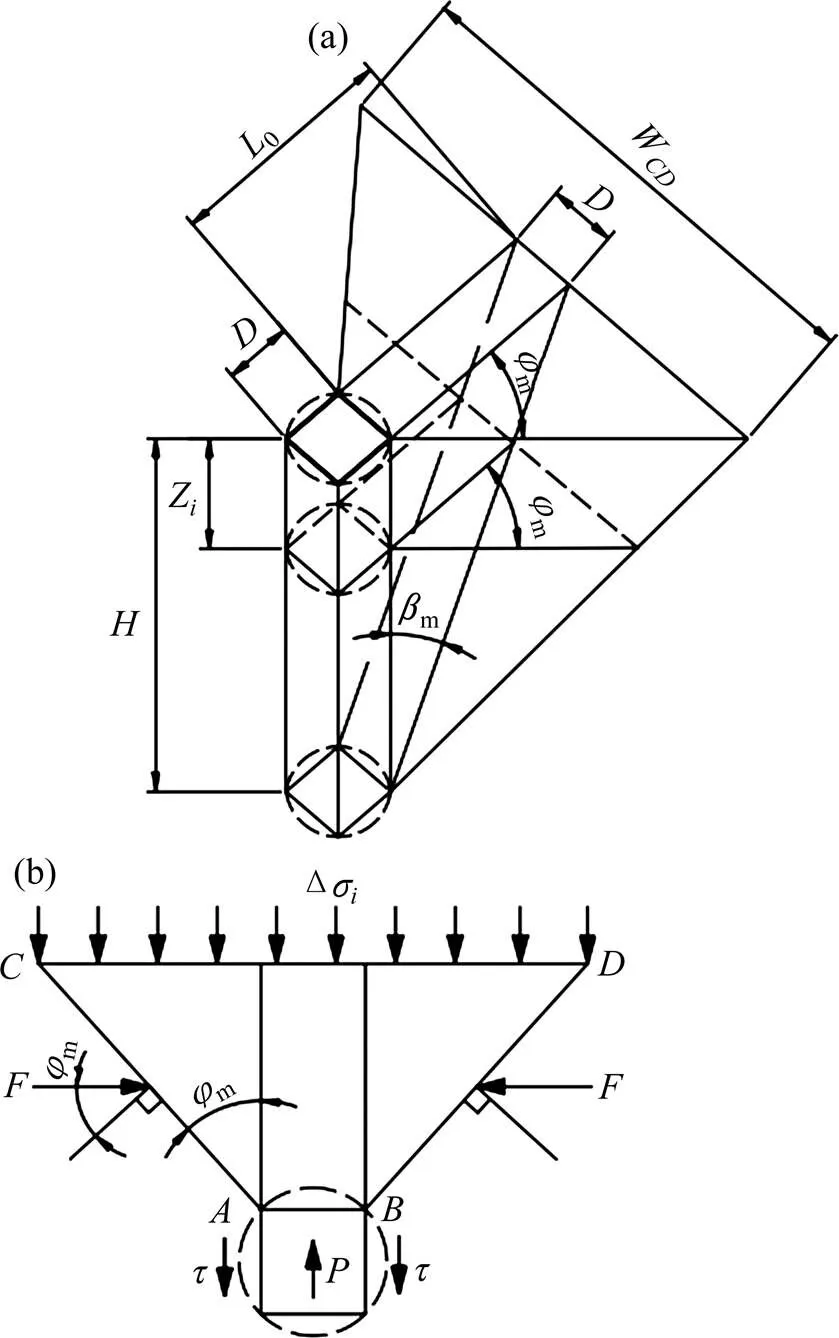
(a) 桩前土楔；(b) 受力情况

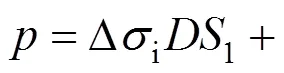
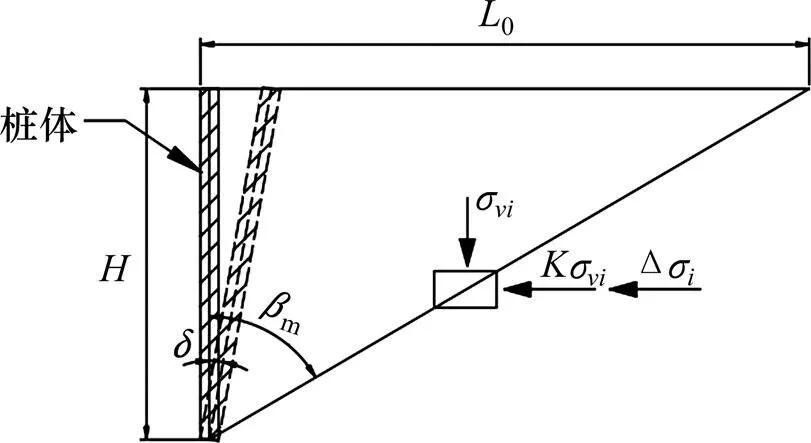
图2 应变楔竖向受力情况及桩变形图

图2中，0表示应变楔的长度；σ表示第层土层的竖向的有效自重应力；Δσ表示第层土层的平均应力增量；表示土压力系数；表示桩身的偏转角，一般假定应变楔深度范围内，桩的变形和深度呈线性关系。

应变楔模型的形体参数如图1中所示，包含：

1) 应变楔伞角(即为内摩擦角发挥值)m[5]，其当土体处于极限破坏状态时，即等于土体的内摩 擦角；

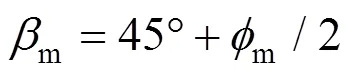
3) 应变楔深度，其中Z表示第层土层深度，表示桩的边长(如果桩为圆桩，表示圆内接正方形边长)；

4) 应变楔的长度0；

5) 应变楔的桩土界面，图1(b)中虚线段表示桩为圆形时的实际桩土界面，实线段表示桩为方形时的桩土界面或者桩为圆形时的等效桩土界面；

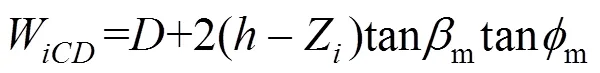
综上所述，利用应变楔模型对横向荷载作用下桩进行受力分析，形体参数的确定至关重要，所以本文拟基于数值分析的结果，探究应变楔形体参数的变化规律，对应变楔模型进行深化与完善。

2 数值模拟分析

2.1 有限元数值模型的建立

使用ABAQUS有限元分析软件建立三维模型，基于应变楔模型假定中桩身变形与深度成线性关系的原因，本文考虑的桩体定为刚性桩。桩体混凝土采用线弹性模拟。砂土算例采用文献[16]的直径为4 cm，入土深度为50 cm的有机玻璃管于1 m3的砂土试验模型槽中单桩基础横向承载力试验的桩土参数，黏土算例采用文献[17]的直径为45 cm，桩长4.5 m的钻孔压浆灌注桩单桩水平静载试验的参数。具体桩土参数如下表所示。

土体的塑性部分选择莫尔库仑模型模拟。为避免边界效应的影响，同时简化模型的复杂程度，径向范围设为半径的20倍。土体参数如表2所示。

表1 桩体的基本参数

表2 土体的基本参数

对于桩土之间的接触特性，其中法向模型选为硬接触，摩擦特性选为罚函数法，桩土摩擦因数取tan(0.75)。并限制土体侧面2个水平方向上的位移以及底部边界上2个水平方向和竖向的位移。

对于砂土模型，单元类型采用C3D8R，对于桩体，沿径向等距布置5个单元，轴向等距布置15个单元，环向等距布置20个单元。对于土体，环向同样等距布置20个单元，沿径向布置12个单元，bias ratio为5。桩侧土轴向同桩一样等距布置15个单元，桩底土轴向布置10个单元，bias ratio为3横向荷载方向为沿轴方向，均布作用于整个桩顶面上。

对于黏土模型，单元类型采用C3D8R，对于桩体，沿径向等距布置3个单元，轴向等距布置8个单元，环向等距布置16个单元。对于土体，环向同样等距布置16个单元，沿径向布置10个单元。桩侧土轴向同桩一样等距布置8个单元，桩底土轴向布置10个单元，横向荷载方向为沿轴方向，均布作用于整个桩顶面上。模型如图3所示。

桩前土体应变等值线图如图4所示。图4的平面图与侧面图也证实了应变楔的存在。

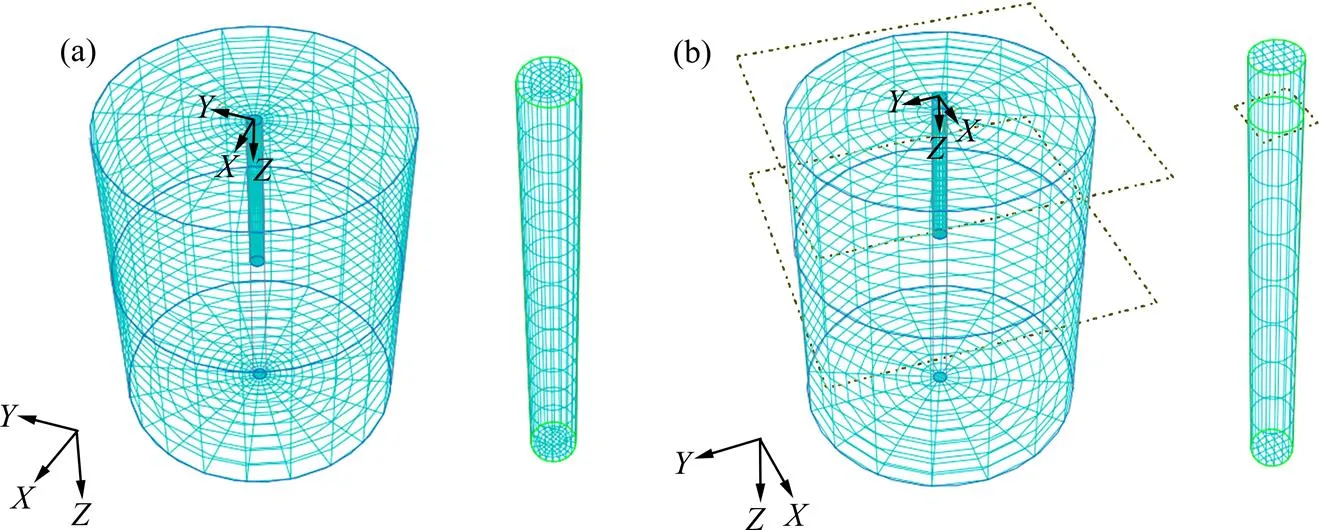
(a) 砂土；(b) 黏土

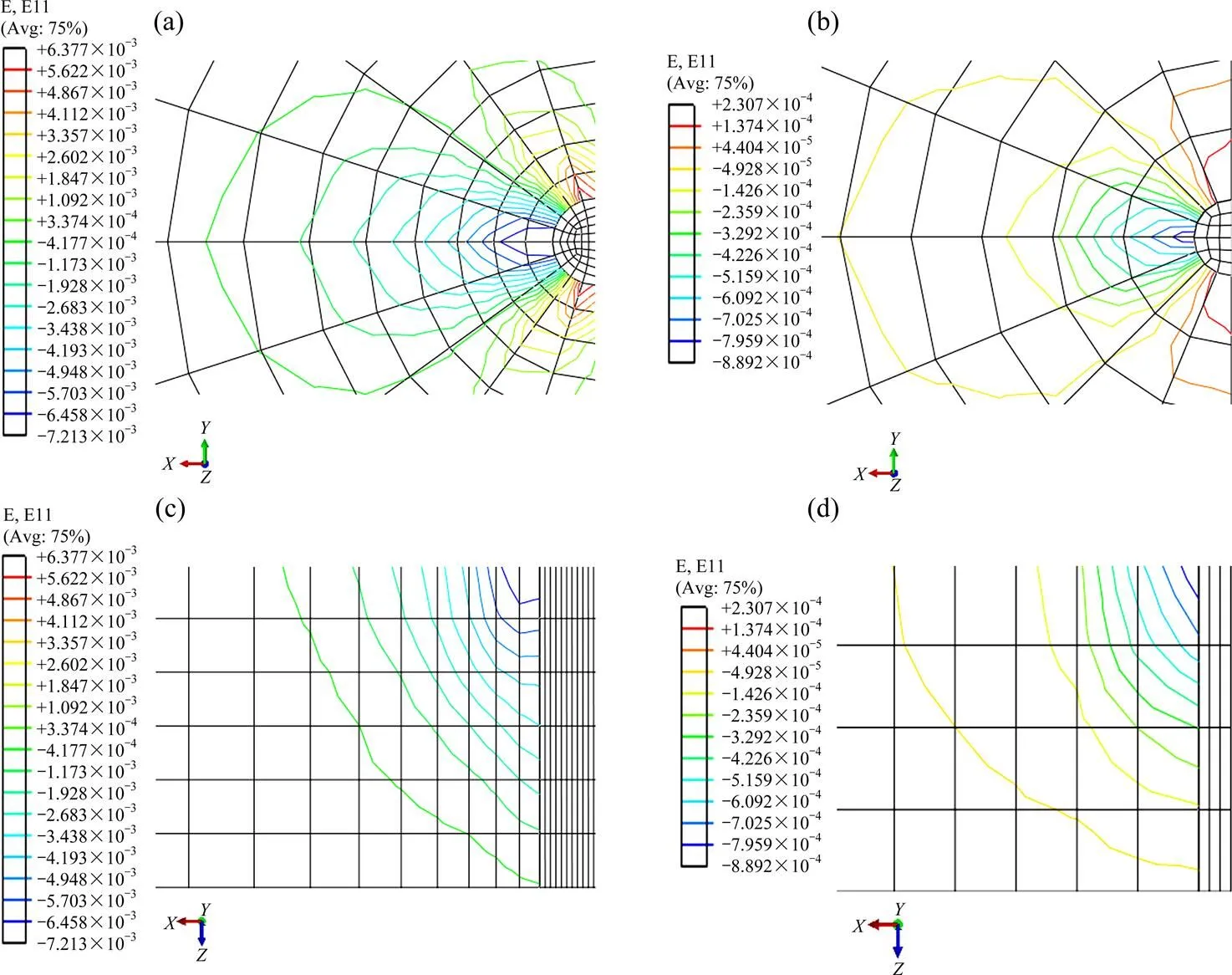
(a) 砂土平面图；(b) 黏土平面图；(c) 砂土侧面图；(d) 黏土侧面图

2.2 模型验证

将计算所得的桩顶位移与荷载曲线同文献[16]进行对比，结果如图5所示。

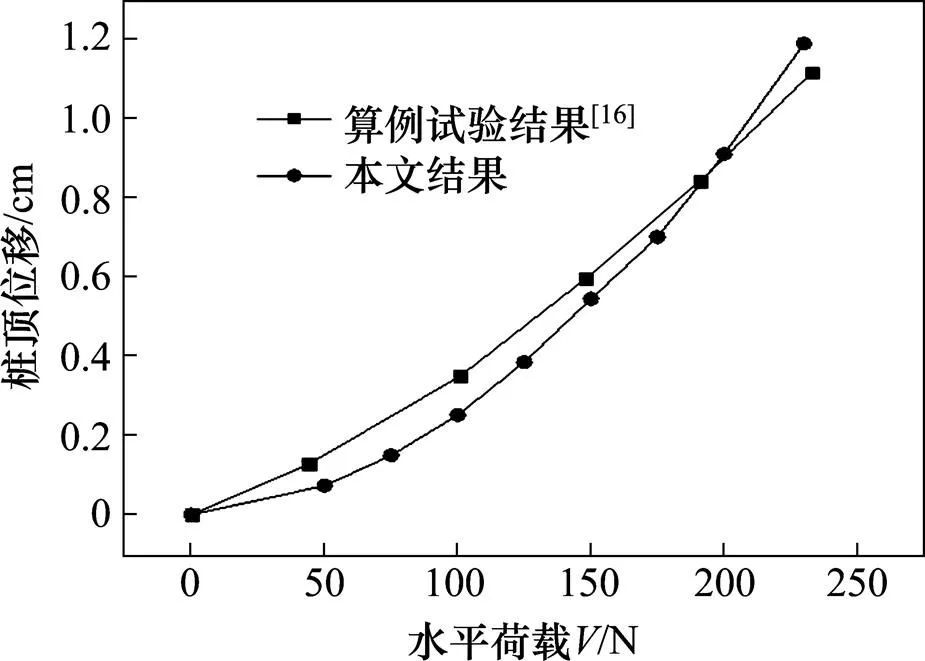
图5 试验与有限元结果对比

由图5可知，基于本文建立的三维有限元模型所得到的结果与算例试验中的桩头位移与荷载曲线变化规律基本一致，且与试验结果相差不大，证明采用本文方法所建立的有限元模型用于分析砂土中横向荷载作用下刚性桩是可行的。其中误差的产生可能是因为建立模型与试验情况存在差异造成的。

采用之前所说方法，利用ABAQUS建立三维有限元模型进行模拟分析，将计算所得的桩顶位移与荷载曲线与文献[17]进行对比，结果如图6所示。

图6 试验与有限元结果对比

从图6可知，基于本文建立的三维有限元模型所得到的结果与算例中的桩头位移与荷载曲线变化规律基本一致，且与试验结果相差不大，证明采用本文方法所建立的有限元模型用于分析黏土中横向荷载作用下桩是可行的。其中误差的产生可能是因为建立模型时未考虑桩内部钢筋及其他与试验的差异造成的。

2.3 应变楔形体参数确定方法

针对以往应变楔模型形体参数大部分采取人为假定或采用经验取值的不足，以砂土中横向荷载作用下刚性桩的有限元分析结果为例，黏土算例分析也采用相同的方法，本文对应变楔各形体参数进行如下定义。

1) 应变楔的边界应变值，通过提取桩土界面路径上的应变，绘制桩土界面图如图7所示。并取圆内接正方形与曲线的交点应变值为边界应变值，即=−0.054 88%。

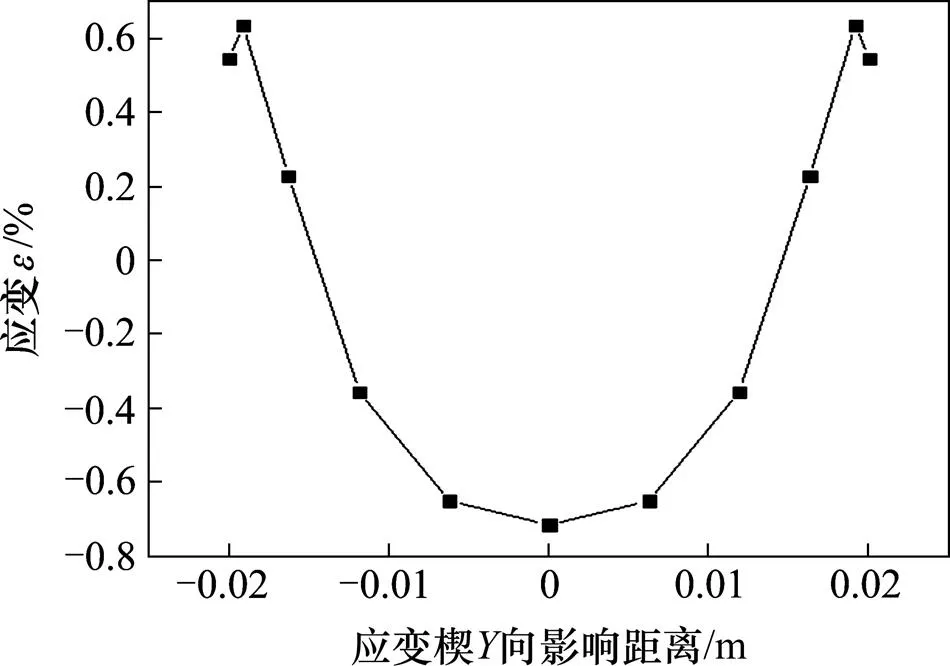
图7 桩土界面ε-Y图

2) 应变楔长度0，通过应变楔长度方向=0时的应变值绘制应变楔-曲线如图8所示，通过已确定的边界应变值=−0.054 88%，即可确定应变楔长度0=0.146 m。

3) 应变楔深度，通过应变楔深度方向的应变值绘制应变楔-曲线如图9所示，通过已确定的边界应变值=−0.054 88%，即可确定应变楔深度=0.192 m。

4) 应变楔底角，模型一般假定应变楔底面为平面，所以可以将应变楔底角m近似取

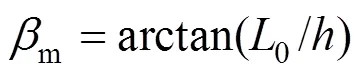
可得m=37.25°。

图8 应变楔图

Fig. 8 Strain wedgediagram

图9 应变楔ε-Z图

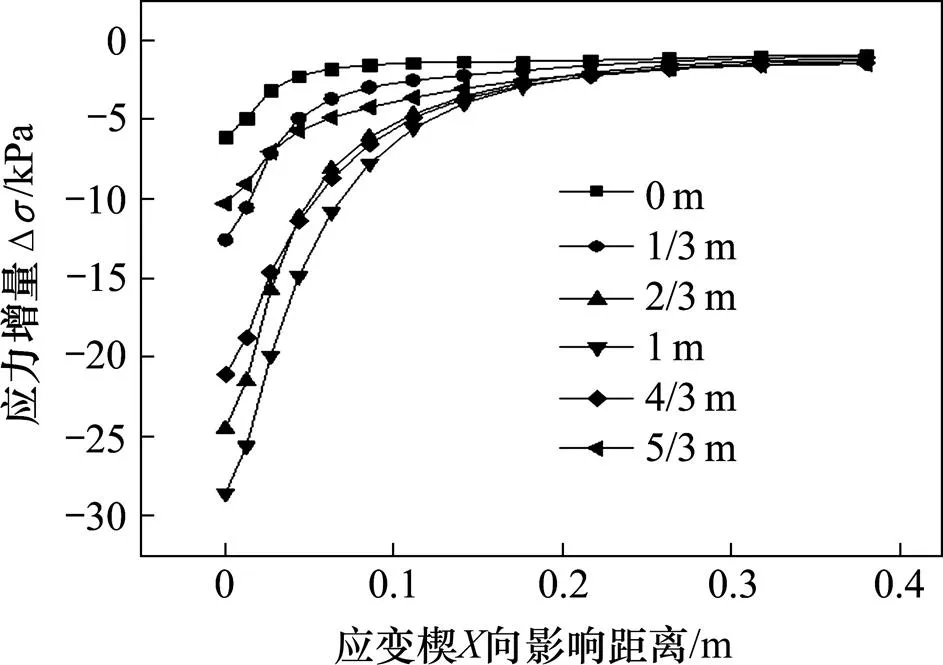
图10 各深度的节点应力值沿X向变化图

5) 应变楔伞角m，通过桩土界面上水平力的平衡方程可以求得应变楔的伞角m：

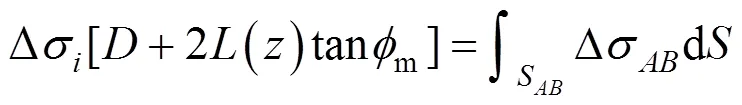
式中：Δσ为应变楔边界的应力增量，如图10所示，取向影响范围()处的应力增量；Δσ为桩土界面S的应力增量(如图11所示)。

图11 各深度桩土界面应力值变化图

Fig. 11 Variation of stress on pile-soil interface in each depths

图12给出了不同深度的伞角值。从图中可以看出，随着深度增加，应变楔的伞角逐渐增加且增幅缓慢减小。为简化后续应变楔模型形体参数变化规律的探究，统一取=0 m处伞角为应变楔伞角。

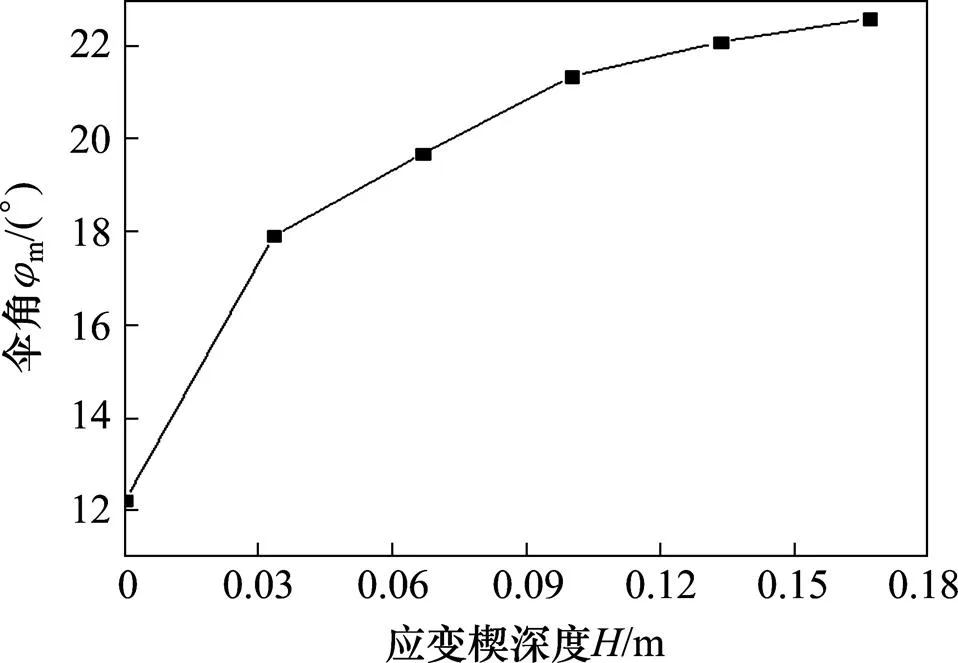
图12 不同深度的伞角值图

3 参数分析

基于第2节中所介绍的确定各应变楔形体参数的方法，将横向荷载，土体弹性模量，土体内摩擦角以及黏聚力视为影响因素，采取控制变量法观察并分析变化时的规律。

3.1 横向荷载变化规律

如表3所示，通过改变横向荷载的大小，考察应变楔模型各形体参数在不同土质下的变化规律。

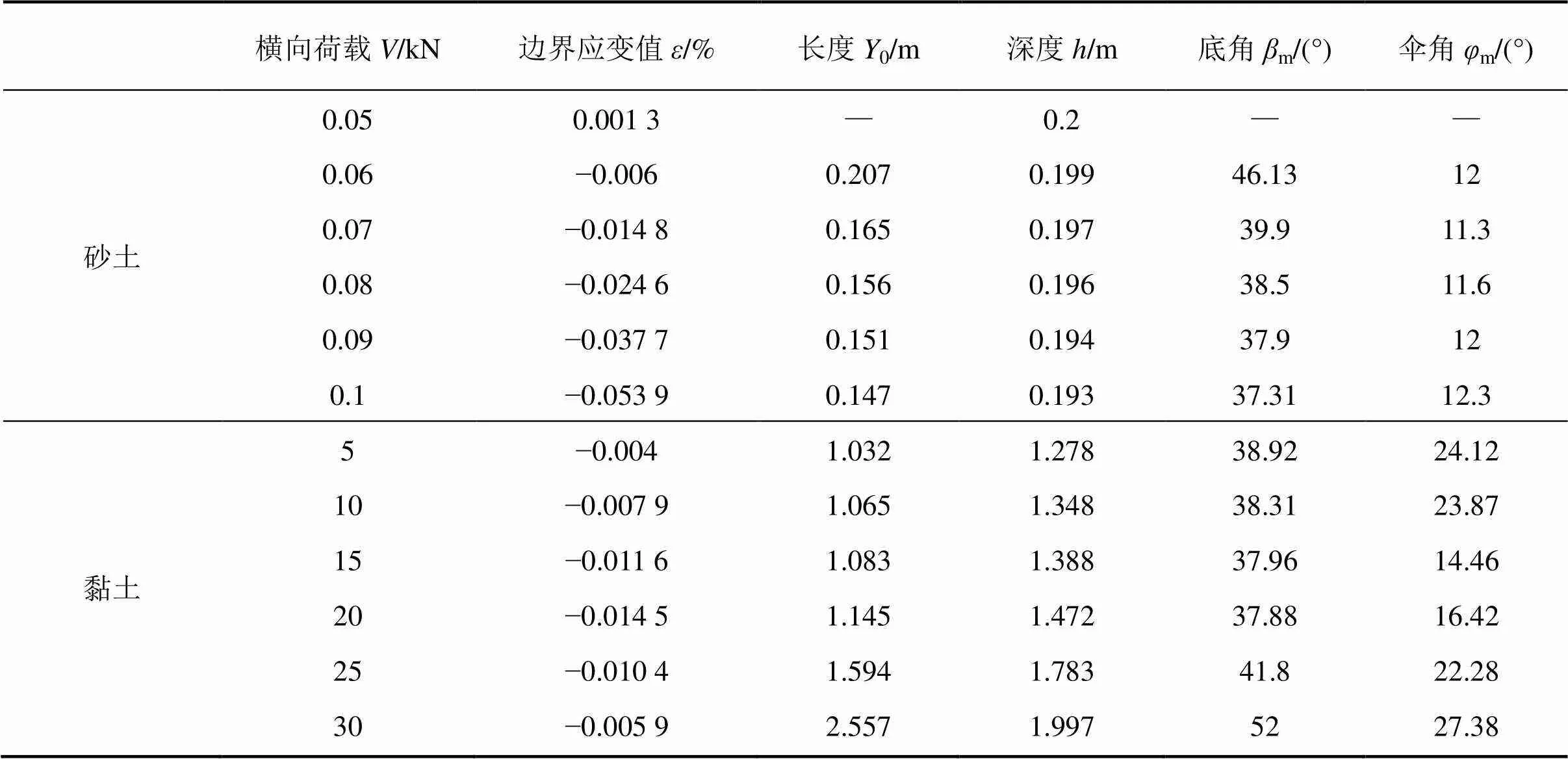
表3 不同水平荷载下应变楔基本参数比较

由表3可以看出，随着横向荷载的增大，砂土与黏土的应变楔长度0，深度，底角m和伞角m均有不同的变化趋势。

3.2 土体内摩擦角变化规律

如表4所示，通过改变土体内摩擦角的大小，考察应变楔各形体参数在不同土质下的变化规律。

表4 不同土体内摩擦角的应变楔基本参数比较

其中砂土摩擦角35.5°是算例中的实际参数，由表4可以看出，随着土体内摩擦角的增大，砂土与黏土中应变楔的边界应变值，应变楔长度0，深度，底角m和伞角m除了砂土的伞角外其余变化均不明显。

3.3 土体弹性模量变化规律

如表5所示，通过改变土体弹性模量的大小，考察应变楔模型各形体参数在不同土质下的变化规律。

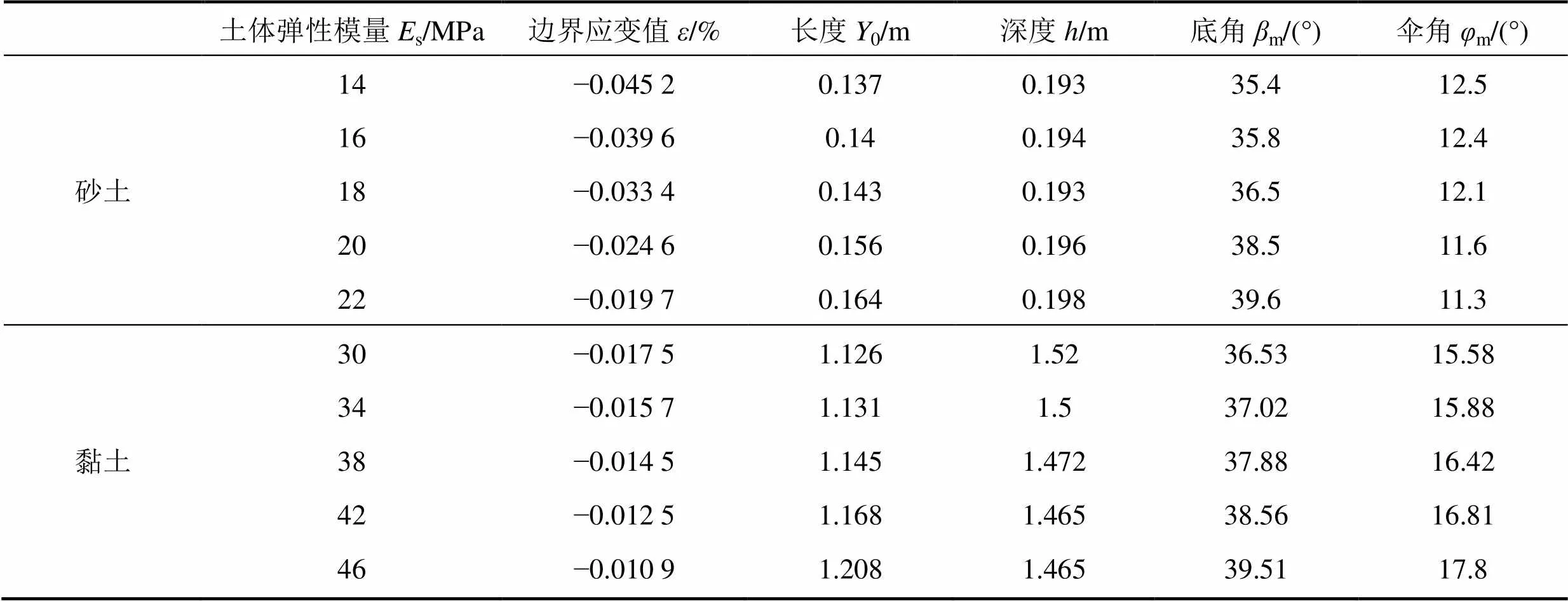
表5 不同土体弹性模量下应变楔基本参数比较

由表5可以看出，随着土体弹性模量s的增加，砂土与黏土中应变楔的边界应变值，应变楔长度0，深度，底角m的变化趋势均基本一致，而伞角m的变化则相反。

3.4 土体黏聚力变化规律

表6对比了应变楔模型形体参数随土体黏聚力变化的情况。

表6 不同土体黏聚力的应变楔形体参数比较

由表6可以看出，随着土体黏聚力的增加，应变楔模型各形体参数未有明显变化，土体黏聚力对桩身位移和应力影响较小，而应变楔形体参数与桩身位移紧密相关。当横向荷载较大时(约100 kN以上)，黏聚力的影响变大，但此时桩顶位移已大于50 mm，远超出一般情况。

由以上分析可知，应变楔模型形体参数在砂土与在黏土中的变化规律有较明显的差异，所以对于应变楔模型，砂土与黏土宜分开考虑。其中土体内摩擦角与弹性模量对各项应变楔形体参数的影响较大，而横向荷载仅对伞角有影响，黏聚力仅在横向荷载很大时有影响，较小时影响很小可以忽略不计。

3.5 拟合公式

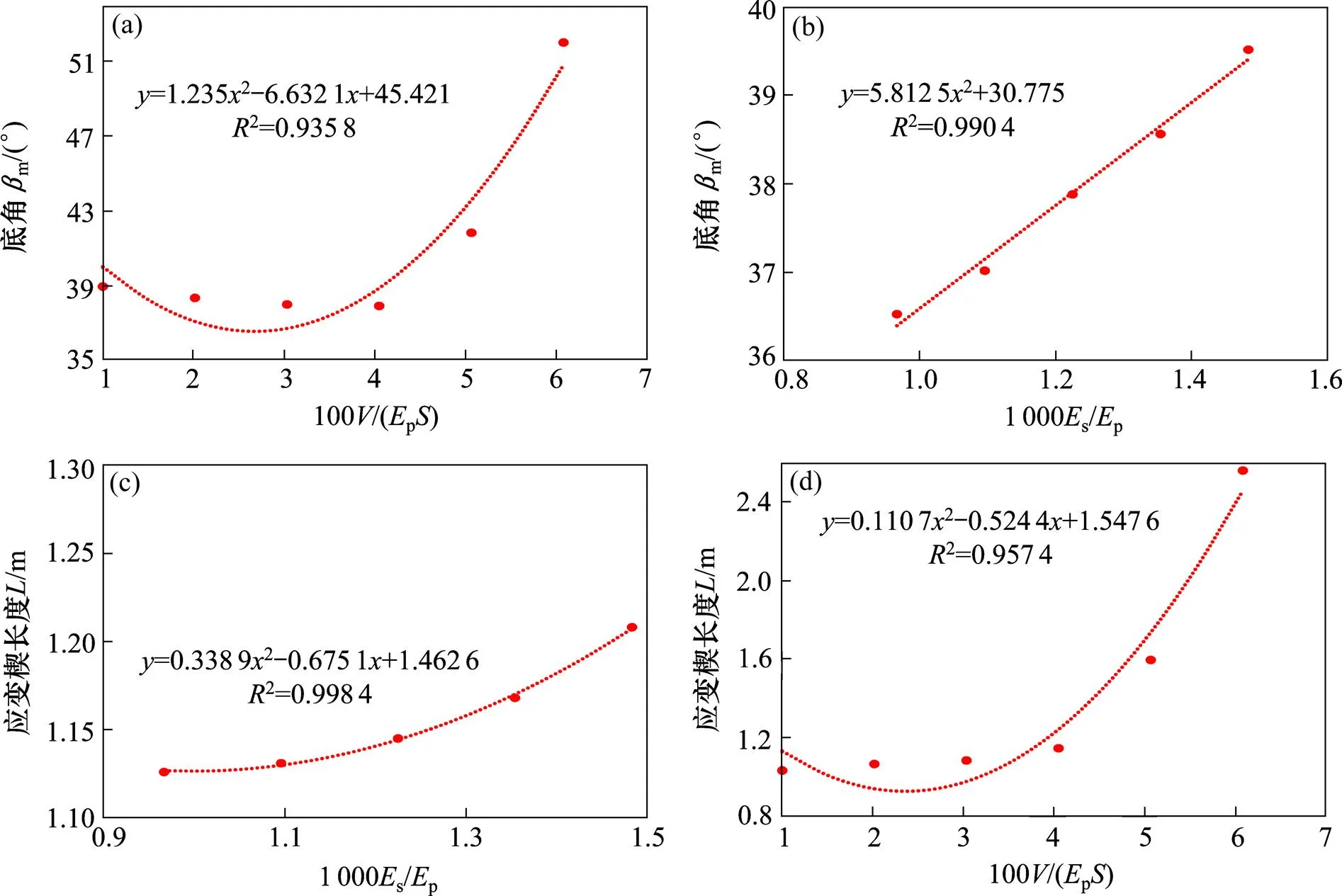
为了综合考虑各影响因素对应变楔形体参数的影响，对确定应变楔的形体参数提供参考，本文对各应变楔影响因素变化规律曲线进行拟合。因为应变楔模型理论中通常假定应变楔的底面为一条直线，所以只要确定应变楔的底角与应变楔的长度即可确定应变楔的底面。基于前文的参数分析，可知砂土与黏土的变化规律有很大的差异，需要分开考虑。故根据本文数值分析的结果(如表3~6所示)对砂土与黏土分别进行回归分析，各曲线代表底角或长度随着变量变化的规律，并对变量进行无量纲化处理(如图13~14所示)，对应变楔的底角与应变楔的长度进行拟合，得到拟合公式如下。

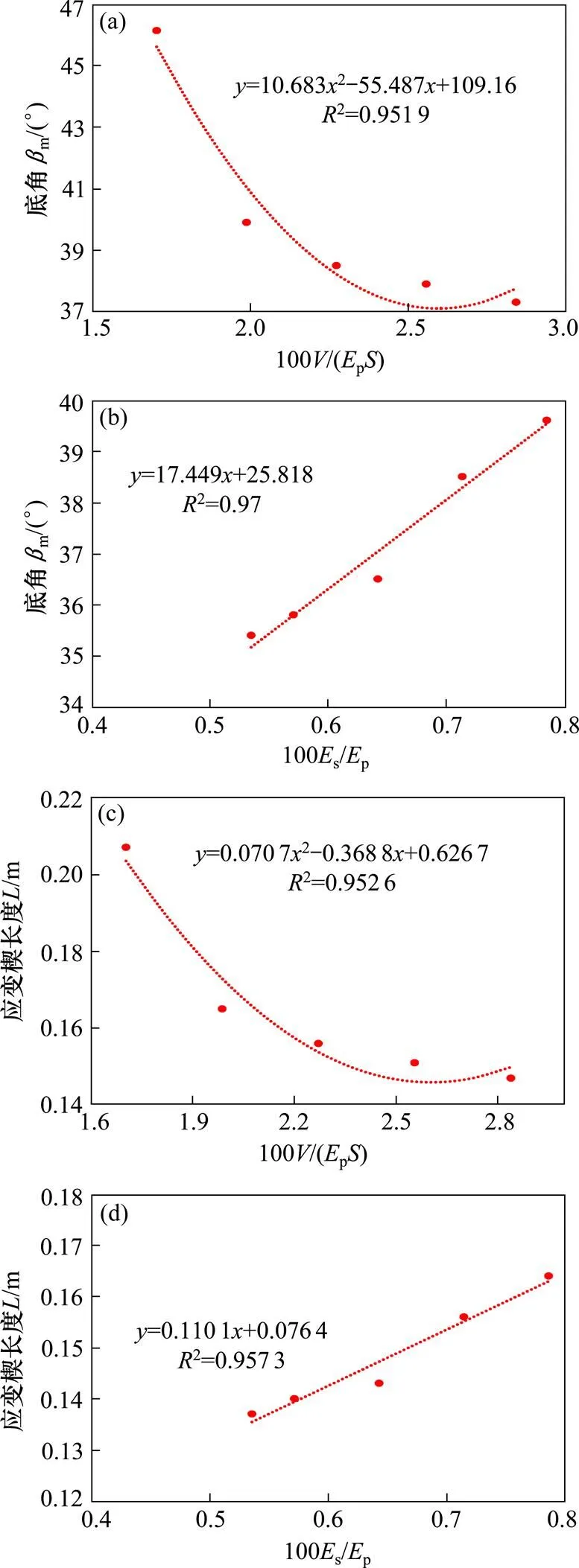
(a) 底角与横向荷载；(b) 底角与土体弹性模量；(c) 长度与横向荷载；(d) 长度与土体弹性模量

图中2表示可决系数，它是反映回归曲线因变量变化可靠程度的一个统计指标。2的取值范围是[0,1]，越接近于1说明拟合曲线的拟合程度越好。

砂土中的应变楔模型底角拟合公式为：

砂土中的应变楔模型应变楔长度拟合公式为

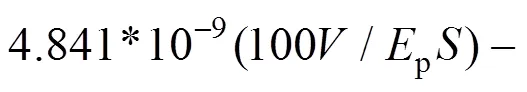
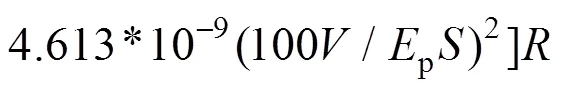
(a) 底角与横向荷载；(b) 底角与土体弹性模量；(c) 长度与土体弹性模量；(d) 长度与横向荷载

黏土中的应变楔模型底角拟合公式为：

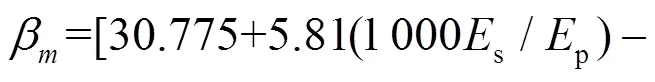
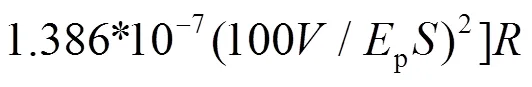
黏土中的应变楔模型长度拟合公式为：

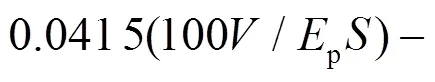
4 结论

1) 通过ABAQUS有限元软件以及现有应变楔模型理论，建立横向荷载作用下刚性桩的三维模型，并且通过算例验证了其合理性。

2) 通过ABAQUS分析结果的应变等值线图，验证了应变楔的存在；并且定义了各应变楔模型形体参数的取值方法。

3) 对比了砂土与黏土中不同横向荷载、土体内摩擦角、土体弹性模量、黏聚力下的应变楔模型形体参数，结果表明砂土与黏土中的应变楔模型形体参数变化规律并不完全相同，需要分开考虑。

4) 分别对砂土黏土的应变楔模型形体参数进行回归分析，拟合出应变楔模型的底角与长度公式。为确定应变楔的形体参数提供参考。

[1] 赵明华, 刘敦平, 邹新军. 基于m法的横向受荷桩无网格伽辽金分析[J]. 公路交通科技, 2008, 25(11): 24−28. ZHAO Minghua, LIU Dunping, ZOU Xinjun. Analysis of lateral loaded piles by element-free galerkin method based on elastic foundation coefficient “m” method[J]. Journal of Highway and Transportation Research and Development, 2008, 25(11): 24−28.

[2] 何益斌, 张铁成, 肖阿林, 等. 极限平衡法分析钢骨−钢管混凝土短桩承载力的简化方法[J]. 铁道科学与工程学报, 2006, 3(5): 46−49. HE Yibin, ZHANG Tiecheng, XIAO Alin, et al. Ultimate strength of short steel tubular column filled with structural steel[J]. Journal of Railway Science and Engineering, 2006, 3(5): 46−49.

[3] 赵明华. 桥梁桩基计算与检测[M]. 北京: 人民交通出版社, 2000. ZHAO Minghua. Calculation and detection of bridge pile foundation[M]. Beijing: China Communications Press, 2000.

[4] Norris G M. The drained shear strength of uniform quartz sand as related to particle size and natural variation in particle shape and surface roughness[D]. Berkeley: University of California, 1977.

[5] Norris G M. Theoretically based BEF laterally loaded pile analysis[C]// Proceedings of the 3rd International Conference on Numerical Methods in Offshore Piling. Paris: Technip, 1986: 361−386.

[6] Ashour M, Norris G, Pilling P. Strain wedge model capability of analyzing behavior of laterally loaded isolated piles, drilled shafts, and pile groups[J]. Journal of Bridge Engineering, 2014, 9(4): 310−311.

[7] Ashour M, Norris G, Pilling P. Laterally loaded isolated piles, drilled shafts and pile groups using the strain wedge model[C]// Geosupport Conference, 2004(124): 800−815.

[8] 李忠诚, 杨敏. 被动桩土压力计算的被动拱–主动楔模型[J]. 岩石力学与工程学报, 2006, 25(增2): 4241−4247. LI Zhongcheng, YANG Min. Passive arching-active wedge model of soil pressure calculation in passive piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl 2): 4241−4247.

[9] Ardalan H, Ashour M. Application of the strain wedge model in soil-pile interaction analysis of pile-stabilized slopes[J]. Geo-congress, 2013, 116(231): 1944−1955.

[10] 陈昌富, 戴宇佳, 梁冠亭, 等. 基于改进SW滑楔模型刚性抗滑桩极限滑坡推力智能优化计算方法[J]. 水文地质工程地质, 2014, 41(6): 38−43. CHEN Changfu, DAI Yujia, LIANG Guanting, et al. Intelligent optimum algorithms of ultimate thrust acting on the rigid anti-slide pile based on modified strain-wedge model[J]. Hydrogeology and Engineering Geology, 2014, 41(6): 38−43.

[11] XU Liangyu, CAI Fei, WANG Guoxin, et al. Nonlinear analysis of single laterally loaded piles in clays using modified strain wedge model[J]. International Journal of Civil Engineering, 2017, 15: 895−906.

[12] 杨明辉, 冯超博, 赵明华, 等. 考虑坡度效应的水平受荷桩应变楔计算方法[J]. 岩土力学, 2018, 39(4): 1−10. YANG Minghui, FENG Chaobo, ZHAO Minghua, et al. Research on the calculation method of laterally loaded pile based on strain wedge model considering slope effect[J]. Rock and Soil Mechanics, 2018, 39(4): 1−10.

[13] 彭芳乐, 大内正敏, 日下部治. 岩体斜面上刚性桩基础水平承载力的三维分析与评价[J]. 岩石力学与工程学报, 2003, 22(6): 1008−1016. PENG Fangle, Ouchi Mashatoshi, Kusakabe Osamu. Three-dimensional analyses on the laternal bearing capacity of rigid pile foundation on rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(6): 1008−1016.

[14] 金青, 崔新壮, 刘正银. 刚性桩横向承载力数值分析[J]. 岩土力学, 2006, 27(10): 814−817. JIN Qing, CUI Xinzhuang, LIU Zhengyin. Study on stability of thin-walled circular pipe piles embedded shallowly under lateral loads[J]. Rock and Soil Mechanics, 2006, 27(10): 814−817.

[15] 张华华. 水平荷载桩的现场试验与数值模拟分析[D]. 扬州: 扬州大学, 2007. ZHANG Huahua. The field test and numerical simulation analysis of lateral loading pile[D]. Yangzhou: Yangzhou University, 2007.

[16] 周龙. 砂土中海上风电超大直径钢管桩桩土相互作用研究[D]. 天津: 天津大学, 2014. ZHOU Long. Research on the interaction between pile and soil of super-large diameter steel pipe piles for offshore wind farm in sand[D]. Tianjin: Tianjin University, 2014.

[17] 王怀德. 刚性短桩基础水平承载性能及数值模拟研究[D]. 合肥: 合肥工业大学, 2015. WANG Huaide. The horizontal bearing capacity and numerical simulation study of rigid short pile foundation[D]. Hefei: Hefei University of Technology, 2015.

Study of laterally-loaded rigid pile strain wedge model shape parameters base on finite element analysis

ZHAO Minghua, LI Shuaichao, PENG Wenzhe

(Geotechnical Institute of Hunan University, Changsha 410082, China)

To research the variation law of body parameters in strain wedge model, a horizontal loading rigid pile numerical model in 3-Dimensional space was established to analysis according to the existing sand and clay testing data with the help of ABAQUS finite element software. First, a horizontal loading rigid pile numerical model in 3-Dimensional space was established by ABAQUS based on the Mohr-Coulomb constitutive model and the discontinuous contact algorithm of penalty function and Linear reduced integral unit, and the model has been verified by examples. Then, the existence of boundary strain has been confirmed according to the analysis result by ABAQUS and shape parameters were determined. Next, the change of shape parameters of strain wedge model under different horizontal load, internal friction angle and elastic modulus of soil are compared and analyzed from sand and clay based on control variable method. Finally, fitting formula of base angle and length of strain wedge in sand and clay has been obtained respectively through regression analysis. The result shows the variation law of strain wedge in sand is not the same as that in clay, so it is best to be considered separately.

lateral load; rigid pile; strain wedge model; finite element; influence factor

10.19713/j.cnki.43−1423/u.2019.03.015

TU473

A

1672 − 7029(2019)03 − 0674 − 10

2018−03−29

国家自然科学基金资助项目(51478178)

赵明华(1956−)，男，湖南邵阳人，教授，从事桩基础及软土地基处理研究；E−mail：mhzhaohd@21cn.com

(编辑 涂鹏)