一种面向无参考的顺轨干涉SAR海面相干时间计算方法

魏翔飞， 种劲松

(1. 中国科学院 电子学研究所， 北京 100190； 2. 微波成像技术国家级重点实验室， 北京 100190；3. 中国科学院大学， 北京 100049)

0 引 言

合成孔径雷达(Synthetic Aperture Radar, SAR)是一种相干成像雷达， 为了获取较高的方位向分辨率， 分辨单元内目标的散射特性在合成孔径时间内需要保持较高的相干性， 即目标需要有较长的相干时间[1]. 中等入射角情况下， 海面回波主要是由海面微尺度Bragg波引起的后向电磁散射信号[2]， 而Bragg波处于时时刻刻的运动之中. 受海面风场、 海面洋流、 长波轨道运动等因素的影响， Bragg波的运动状态较为复杂， 导致海面的整体散射特性在合成孔径时间内难以保持较高的相干性. Raney[3]首先研究了相干时间对SAR成像的影响， 认为当相干时间小于SAR系统积分时间时， 方位向有效积分时间会减小， 从而导致SAR方位向有效分辨率下降. 因此， 若海面相干时间小于SAR系统积分时间， SAR对海面成像时其方位向分辨率会下降[4]. 方位向分辨率下降会影响SAR对小尺度海洋现象的成像能力， 导致SAR海浪图像出现所谓的“方位截断”现象[5-8]， 这会对海浪谱的反演造成影响. 此外， 在利用ATI-SAR反演海面流场时， 海面有限的相干时间会限制干涉基线的长度， 从而影响流场反演的精度. 因此， 研究海面相干时间对于SAR海面成像及其应用具有十分重要的意义.

顺轨干涉SAR(Along-Track Interferometric SAR， ATI-SAR)通过计算前后通道之间的相关系数来计算海面相干时间. 在不考虑噪声且成像区域相干时间无限长的情况下， 前后两个通道图像的相关系数为1. 实际情况中， 在噪声和有限的海面相干时间的共同影响下， ATI-SAR前后通道之间的相关系数小于1. 因此， 利用ATI-SAR计算海面相干时间时， 需要知道噪声引起的相关系数的下降. 在估计出噪声引起的相关系数的下降后， 根据前后两个通道图像间的相关系数和成像时间差， 即可计算出海面相干时间. Shemer[9]以SAR图像中包含的陆地区域作为基准， 估算噪声引起的相关系数的下降. Carande[1]则利用双基线干涉SAR中基线长度为零的干涉数据计算噪声引起的相关系数的下降. 然而， 通常获取的ATI-SAR数据多为单基线干涉数据， 且图像中往往不包含陆地区域. 尤其是对于机载ATI-SAR， 由于其幅宽较窄， 多数情况下不能覆盖陆地. 当图像中不包含陆地区域， 即图像中不存在参考区域时， 上述方法不再适用.

针对这一问题， 本文提出了一种面向无参考的ATI-SAR海面相干时间计算方法. 该方法首先从ATI-SAR单视复图像(Single-look Complex， SLC)的方位向功率谱中估计出噪声能量， 计算图像的信噪比(Signal-to-Noise Ratio, SNR)； 然后根据信噪比计算前后两个通道之间由噪声引起的相关系数的下降； 最后， 根据两个通道图像之间的相关系数和成像时间间隔， 计算出海面相干时间. 在整个处理过程中， 不需要其它参考信息. 将该算法应用于机载ATI-SAR数据， 获取了海面相干时间. 为了验证实验结果的准确性， 利用海面相干时间的理论计算模型进行了仿真研究. 仿真结果显示， 采用本文算法获取的海面相干时间与理论值较为吻合， 验证了本文算法的有效性.

1 面向无参考的ATI-SAR海面相干时间计算方法

本文提出的面向无参考ATI-SAR海面相干时间计算方法的流程如图 1 所示， 整个流程分为5步： 数据配准、 噪声功率估计， 噪声去相关效应分块计算、 前后通道相关系数分块计算以及海面相干时间计算. ① 采用常用的相关系数法[10,11]对前后两个通道的SLC图像进行配准； ② 利用SLC图像的方位向功率谱， 分别估计两个通道的噪声功率；③ 对前后通道的数据进行分块， 并分别计算每一子块数据的信噪比， 进而计算出噪声引起的相关系数的下降； ④ 计算前后两个通道之间对应子块数据的相关系数； ⑤ 利用前两步的计算结果以及前后通道的成像时间差， 计算出该数据块对应的相干时间. 对每一子块数据进行相同的处理， 即可获得海面相干时间的分布图.

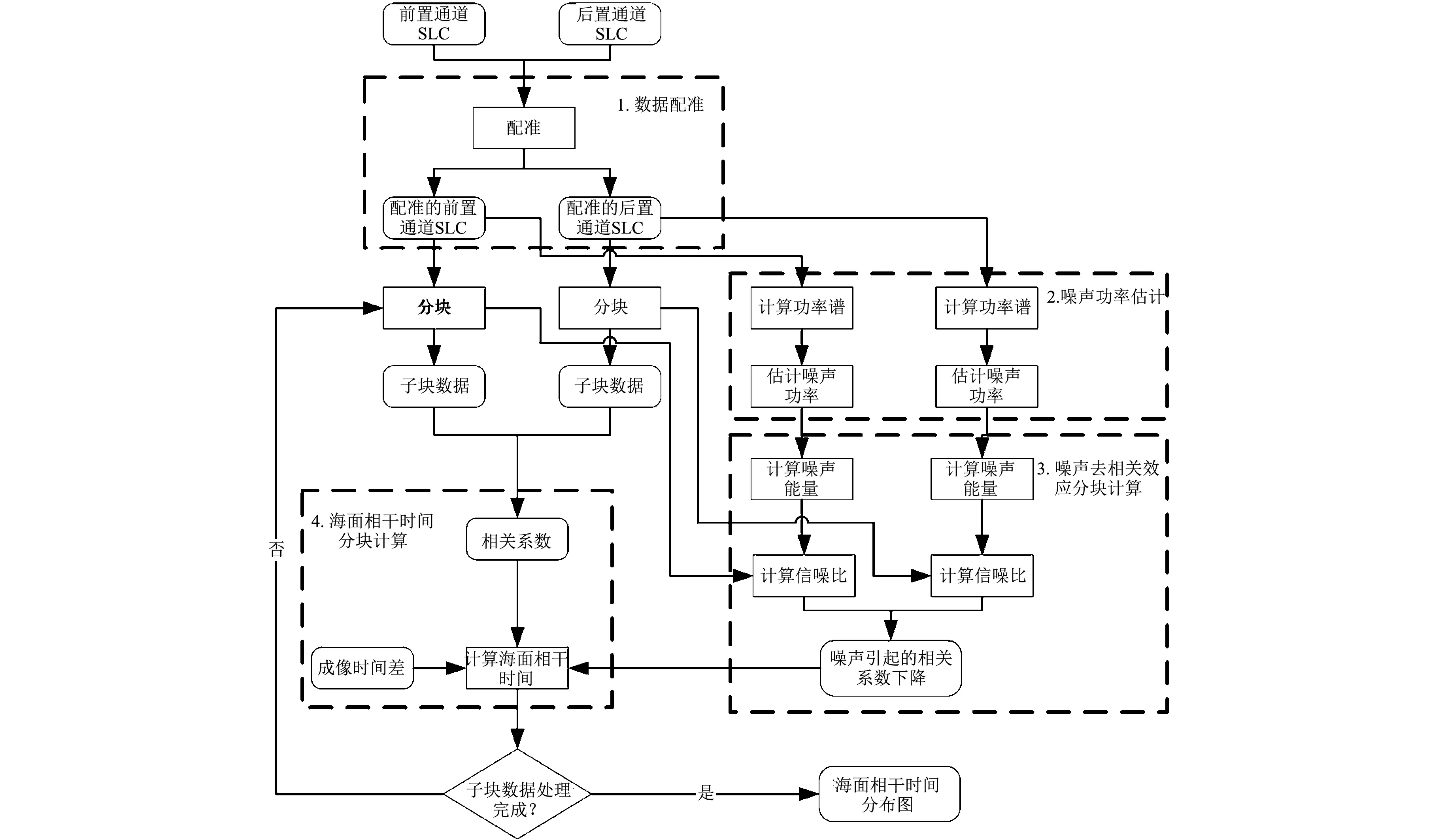
图 1 面向无参考的ATI-SAR海面相干时间计算方法流程图Fig.1 Flow chart of the calculation method for ocean coherence time by along-track interferometric SAR without control point

1.1 噪声功率估计

分别从前置通道和后置通道SAR图像的方位向功率谱中估计出噪声功率， 进而计算出由噪声引起的前后两幅图像相关系数的下降是整个算法中的核心步骤. SAR是一种相干雷达， 其图像的相干斑为乘性噪声[12]， 因此SAR方位向图像可以表示为[13]

I(x)=I0(x)[1+ε(x)],

(1)

式中：x为方位向位置；I0(x)为方位向信号；ε(x)为均值为零的噪声.ε(x)的空间相关统计特性依赖于SAR系统带宽， 且与场景的运动无关[3].

一般来说， 可以认为噪声是空间不相关的， 即ε(x)为空间白噪声. 若以Sε(f)表示其功率谱密度， 则Sε(f)为一常数. 方位向图像I(x)的功率谱密度可以表示为

SI(f)=SID(f)+Sn(f),

(2)

式中：SI0(f)为I0(x)的功率谱密度，

SI0(f)=|FFT{I0(x)}|2,

(3)

Sn(f)为SI0(f)与Sε(f)的卷积， 则Sn(f)也可以用一个常数表示[14].Sn(f)即为SAR图像功率谱密度的噪底， 其表达式为[15]

(4)

式中：N0为噪声功率；PRF为SAR系统的脉冲重复频率. 从式(2)和式(4)可以看出， SAR方位向图像的功率谱密度可以表示为信号的功率谱密度与常数噪底之和. SAR图像的方位向带宽

(5)

式中：V为SAR平台速度；D为天线的物理孔径. 在实际中， 为了防止出现方位混叠， SAR系统的方位采样率一般大于方位向带宽， 即满足

PBF=α·Ba,

(6)

式中：α为大于1的常数. 因此， 可以认为信号的能量只存在于带宽为Ba的频带之中， 而该频带之外不包含信号的能量. 故对SAR方位向功率谱密度来说， 可以认为其边缘位置的值即为噪底[16]. 因此， 利用SAR方位向功率谱密度边缘位置的值乘以PRF， 即可估计出噪声功率. 实际处理中， 可以从SAR图像中选取一小块区域来估计噪声的功率. 同时， 为了使估计结果更准确， 在计算方位向功率谱时， 可以在该区域的不同距离门之间取均值.

1.2 噪声去相关效应分块计算

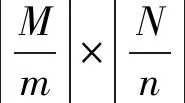
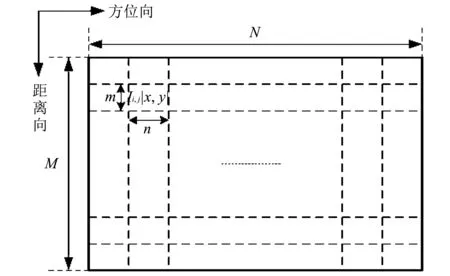
图 2 SAR图像分块示意图Fig.2 Schematic diagram of SAR image segmentation

(7)

因此， 其

(8)

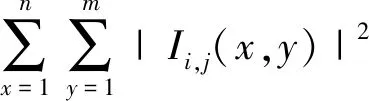
对该数据块来说， 由噪声引起的去相关[17]

(9)

若前后两个通道具有不同的SNR， 则式(9)变为[1]

(10)

式中：

(11)

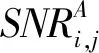
(12)

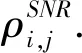
1.3 海面相干时间分块计算

计算分块数据之间的相关系数， 其表达式为

(13)

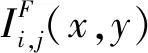
(14)

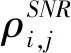
(15)

式中：τc为海面相干时间；

(16)

为前后两个通道的成像时间差；B为干涉基线长度；vp为平台速度. 根据式(10)、 式(13)～式(16)， 可以计算出海面相干时间

(17)

2 实验结果与分析

2.1 机载ATI-SAR数据处理结果

利用中国科学院电子学研究所的C波段机载ATI-SAR数据对所提的算法进行验证. 该数据获取于2016年3月21日， 雷达系统参数如表 1 所示. 其中， 前后接收通道之间的距离为0.9 m， 由于共用一个发射通道， 因此干涉基线长度为0.45 m.

表 1 机载ATI-SAR系统参数Tab.1 Parameters of the airborne ATI-SAR system

如图 3 所示， 实验中获取了较大范围的海洋数据. 其中，
图 3(a) 为前置通道的幅度图像，
图 3(b) 为后置通道的幅度图像.
图中左边黑色区域为海面油膜， 右边亮目标为海面舰船. 该数据块的大小为9 000×24 000(距离向×方位向)像素， 分辨单元大小为0.2 m×0.2 m， 其近端斜距约为3.3 km， 远端斜距约为5 km， 场景中心的入射角为60°.

在采用相关系数法对上述两个通道的图像进行配准后， 利用图像的方位向功率谱估计噪声功率. 选取图 3 中白色方框区域， 其大小为 1 500×3 500(距离向×方位向)像素， 求出该区域对应的功率谱密度如图 4 所示. 根据表 1 中的数据， 可以计算出SAR图像的方位向带宽约为 400 Hz， 而SAR系统的方位向采样率为 5 000 Hz， 远大于图像的方位向带宽， 满足从功率谱密度中估计噪声功率的条件. 从图 4 中可以看出， 功率谱密度为信号的功率谱与噪底之和， 功率谱边缘位置的值即为噪声的功率谱密度， 且前后通道的噪声功率并不相同.

图 3 实验中获取的海面SAR幅度图像Fig.3 SAR amplitude image of sea surface obtained in the experiment

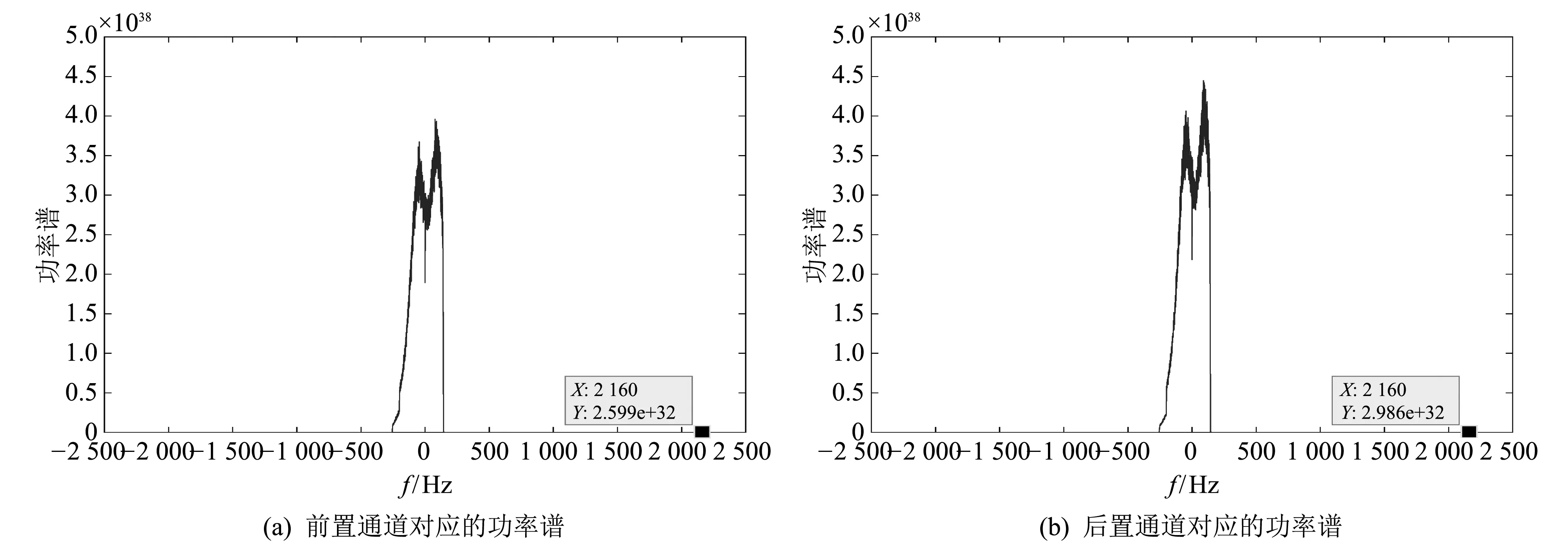
图 4 白色方框区域对应的功率谱Fig.4 Power spectrum of the white box area

接下来， 对数据进行分块， 这里取分块大小为30×30. 对每一块， 利用式(7)计算出该块数据包含的噪声能量； 根据式(8)计算出相应的信噪比； 利用式(10)计算出由噪声引起的相关系数的下降. 在完成上述步骤之后， 通过前后通道之间的相关系数以及成像时间差， 即可计算出该块数据对应的相干时间.
图 5 为利用本文算法获取的海面相干时间的空间分布图， 由于在计算中需要对数据分块， 且每一块数据最终只能得到一个相干时间值， 因此其分辨率比图 3 中幅度图的分辨率要低.

图 5 本文方法获取的海面相干时间分布图Fig.5 Ocean coherence time distribution obained by proposed method

图 5 左边相干系数较低的区域为幅度图中的油膜区域. 由于油膜的散射率一般较低， 其相干性较差， 因此油膜区域的相干时间较短. 从图 5 中可以看出， 油膜区域的相干时间大多在10 ms以下， 而其它区域的相干时间大多分布在10～100 ms 之间.
图中沿方位向的细线是由于系统本身的干扰而形成的， 由于系统干扰的相干性较差， 因此这些直线也呈现出较低的相干时间.

图 6 为相干时间的统计分布， 可以看到相干时间分布在5～100 ms之间， 其中较低的相干时间(5～10 ms)为油膜区域和系统干扰对应的相干时间， 而海面的相干时间分布在10～100 ms之间.

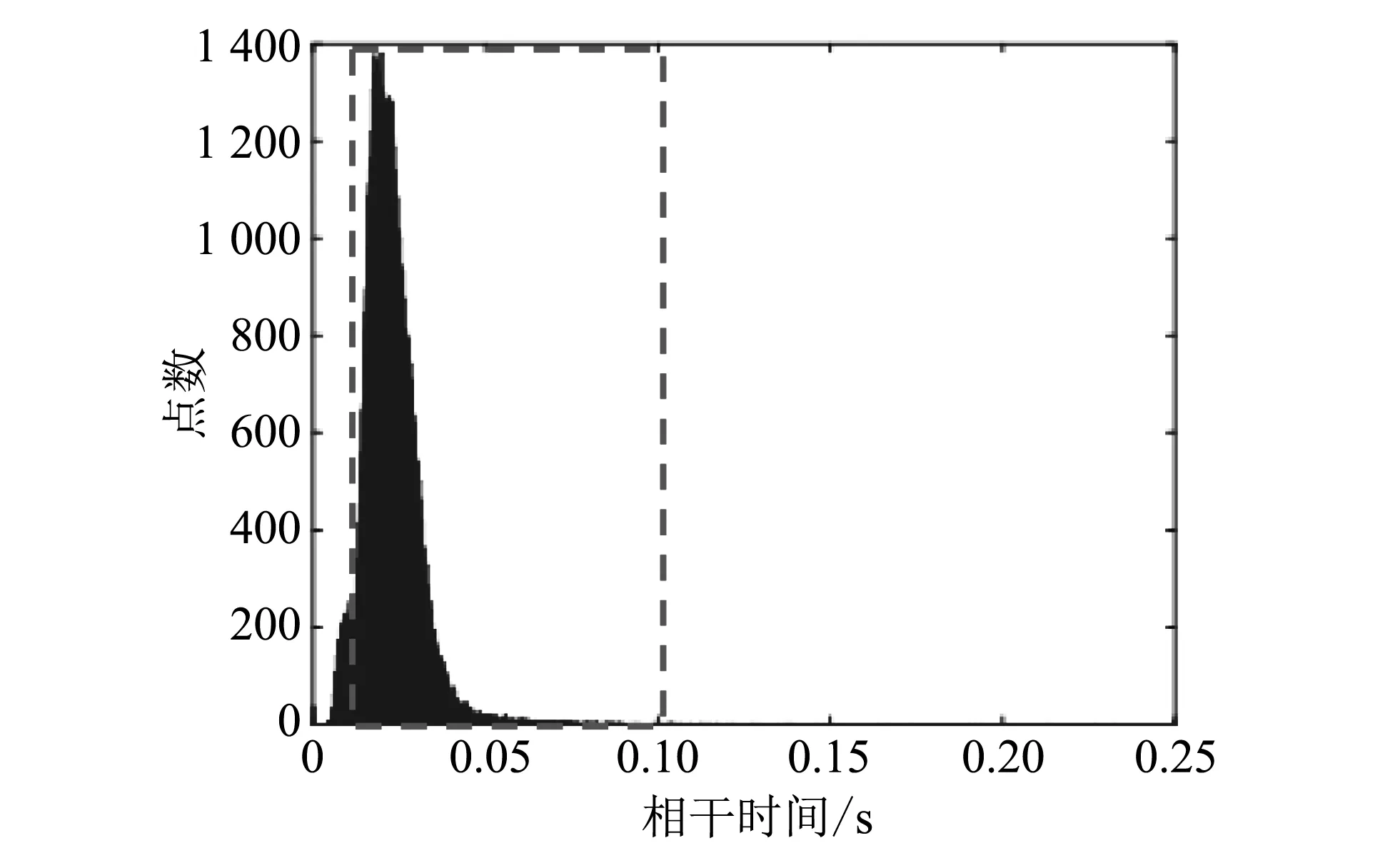
图 6 海面相干时间的统计分布Fig.6 Statistical distribution of the ocean coherence time

2.2 实验结果验证

用海面相干时间的理论计算模型， 对本文实验条件下海面相干时间进行仿真研究. 海面相干时间的理论计算公式为[19]

|g|2=cos2θ+sin2θsin2φ,

(18)

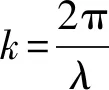
s(k,φ)=s(k,0)D(k,φ),

D(k,φ)=sech2(Bφ),

(19)

式中：φ为海浪传播方向与风向的夹角；α,kp,G,H都是与风速有关的参数. 从式(18)和式(19)可以看出， 海面相干时间受雷达波段、 入射角、 海面风速、 雷达视向与风向夹角等影响. 实验中， 雷达波长、 入射角为已知信息， 而海面风场信息未知. 因此， 这里仿真研究了C波段、 入射角60°时， 海面相干时间与海面风速和风向之间的关系， 仿真结果如图 7 所示.

图 7(a) 为不同风向下海面相干时间随风速的变化曲线，
图 7(b) 为不同风速下， 海面相干时间随风向的变化曲线. 从仿真结果中可以看出， 海面相干时间主要受海面风速的影响， 风速越高， 海面相干时间越短. 雷达视向与风向的夹角对海面相干时间的影响相对较小， 且风速越大， 风向对相干时间的影响就越小. 同时仿真结果表明， 在本文的实验条件下(C波段， 入射角60°)， 海面相干时间在10～150 ms之间.

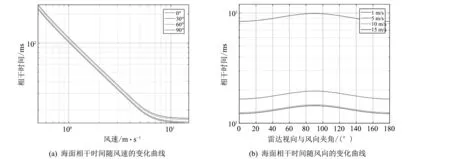
图 7 海面相干时间的理论仿真结果Fig.7 Theoretical simulation results of ocean coherence time

本文处理结果与仿真结果的对比如表 2 所示. 从表 2 中可以看出， 本文方法获取的海面相干时间在10～100 ms之间， 处于理论值10～150 ms 的范围之内， 这表明本文算法在没有陆地目标等参考时， 能够获取较为准确的海面相干时间. 为了验证本文方法的有效性， 表 2 同时给出了直接利用前后通道之间的相关系数计算得到的海面相干时间. 可以看到， 由于没有考虑噪声对相关系数的影响， 直接利用前后通道之间的相关系数得到的海面相干时间存在较大误差.

表 2 海面相干时间的实验结果和仿真结果Tab.2 Experiment and simulation results of ocean coherence time

3 结束语

针对利用ATI-SAR计算海面相干时间时需要其它参考信息这一问题， 本文提出了一种无参考的ATI-SAR海面相干时间计算方法. 该算法利用SAR图像功率谱密度边缘位置的值等于噪声功率谱密度这一特点， 从图像的功率谱密度中估计出噪声能量， 得到信号的信噪比， 并最终计算出海面相干时间. 将本文算法应用于机载ATI-SAR数据， 获取了实验海域的海面相干时间. 同时， 将实验结果与海面相干时间理论计算结果进行对比， 结果表明， 本文算法能获取较为准确的海面相干时间， 证明本文算法具有较高的准确性.

SAR对海面成像时， 当积分时间超过海面相干时间后， 增大积分时间不会显著提高方位向分辨率. 当积分时间较长时， 受海面散射体加速度的影响， 方位向分辨率反而会下降. 为了达到最佳的方位分辨率， 需要根据海面相干时间合理地选择系统积分时间. 因此， 本文方法及实验结果对用于海面成像的SAR系统积分时间的设计具有一定的指导作用. 此外， 在利用ATI-SAR反演海面流场时， 海面相干时间会直接影响流场反演的精度. 为了提高流场反演的精度， 需要选择一个较短的干涉基线， 而基线长度较短时又会影响ATI-SAR的测流灵敏度. 在设计应用于海面流场反演的ATI-SAR时， 需要折衷考虑上述因素， 选择合理的基线长度. 因此， 本文算法及实验结果对ATI-SAR基线长度的设计也有一定的参考意义.