关于恐龙化石在发掘过程中因应力释放造成风化破坏的研究

张尚坤,于学峰,贾超,杜圣贤,田京祥,宋香锁,陈文芳

(1.山东省地质科学研究院，国土资源部金矿成矿过程与资源利用重点实验室，山东省金属矿产成矿地质过程与资源利用重点实验室，山东 济南 250013;2.山东大学土建与水利学院，山东 济南 250013)

0 引言

造成恐龙化石风化破坏的因素众多，许多学者对此做了广泛而深入的研究[1-2]，并在恐龙化石发掘中采取了针对性的有效保护措施，取得了很好的效果。然而，也有的对在恐龙化石发掘过程中产生的破坏作用重视不够，从而因机械扰动直接导致化石或其围岩的破碎，对这种肉眼可见的人为破坏，施工中若制定一些防范措施，是可以避免的。但是，对恐龙化石发掘过程中因应力释放造成的风化破坏缺乏深入的研究。

恐龙化石形成以后，随着埋藏深度的增加和岩石固结程度的提高，化石所承受的应力也会越来越大[3]，化石挖掘会导致深部岩石骤然释重，由此会使化石形成应变，产生节理裂隙，这些节理裂隙为水和空气的活动提供了通道，使风化破坏作用更加迅速。

1 分层开挖理论基础和模型建立

分层开挖法是恐龙化石挖掘过程中最常用的一种方法，即从顶部自上而下分梯段逐层向下开挖。这种方法的主要优点是用一般机械设备即可进行施工，施工简单，且能够最大限度的减小施工中机械振动对化石的破坏。依据分层开挖的理论[4]，建立模拟化石开挖过程的数值模型如图1所示:模型长15m，宽15m，高25m；化石埋深在10m到20m之间，每高差1m分布一层化石；在数值模拟分层开挖过程时，自地表算起共开挖20层，每层开挖厚度为1m，呈梯形分布，化石分布于第11层至第20层之间。每层化石分布裸露部分大小为化石的1/3、1/2和2/3共3列。

a—几何模型;b—数值模型图1 恐龙化石发掘过程模型

模型边界条件：底部采用固定约束，左右两侧约束x方向位移，前后两侧约束y方向位移，整个开挖过程中模型存在重力作用。该三维模型中，化石及围岩的材料特性均按均值弹塑性考虑，采用Drucker-Prager屈服准侧[5-6]。公式见式(1)：

-αI1-k=0

(1)

式中：I1为应力张量第一不变量；J2为应力偏张量第二不变量。α,k均为与岩土材料粘聚力c和内摩擦角φ有关的常数。其关系式如下：

(2)

(3)

在MSC.Marc软件中，Drucker-Prager准则的实现是通过与Mohr-Coulomb准则之间的参数关系实现的。故在MSC.Marc软件中输入的参数α,σ表达式如式(4)：

(4)

根据标准试件的实验结果及相关资料取模型参数如表1。

2 化石在发掘过程中应力变化分析

恐龙化石及围岩体内初始地应力的大小主要与其自重应力和构造应力有关，而构造应力是长期地质构造运动的结果，它随着时间的推移会不断发生变化，是非稳定应力场，而且构造应力目前尚无法用数学力学的方法进行计算，所以该课题中忽略构造应力的影响，初始地应力场采用初始重力场。

表1 分层开挖模型参数

随着化石发掘过程中开挖深度的增加，各层化石及围岩的应力场不断变化，由于篇幅所限，这一部分只列出开挖深度为0m，11m，15m，19m时的等效应力图形和XZ方向剪应力图形进行分析对比。

(1)等效应力变化过程

为分析发掘过程中不同埋深化石的应力变化情况，以及相同埋藏深度，化石发掘出的裸露程度(裸露部分所占比例)不同时的应力变化情况，下面列出开挖过程中的等效应力(Equivalent Von Mises Stress)图(图2)和不同埋深、裸露体积所占比例不同的化石及围岩开挖过程等效应力变化曲线(图3)进行分析对比。

Von Mises等效应力的数学表达式[7-9]：

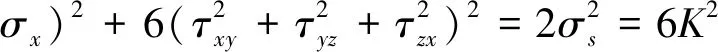
(5)

用主应力表示为:

(6)

式中：σs为材料的屈服点；K为材料的剪切屈服强度。

(7)

由图2中等效应力变化图形可以看出，随着化石的发掘，开挖深度越来越大，各处的化石和围岩应力不断发生变化，开挖前后化石表面的最大等效应力差达到0.34MPa,围岩表面的最大等效应力差达0.3MPa。并且由图2可见，同等深度下，化石和围岩的应力分布并不相同。所以，在化石开挖过程中会导致化石和其围岩的应力分布不均，根据模拟结果,部分相邻位置化石和围岩的应力差达到0.12MPa它们之间会产生力的相互作用，必然导致卸载裂隙的产生，同时开挖过程中的机械扰动也会促进裂隙的产生，从而会加速风化的进行。

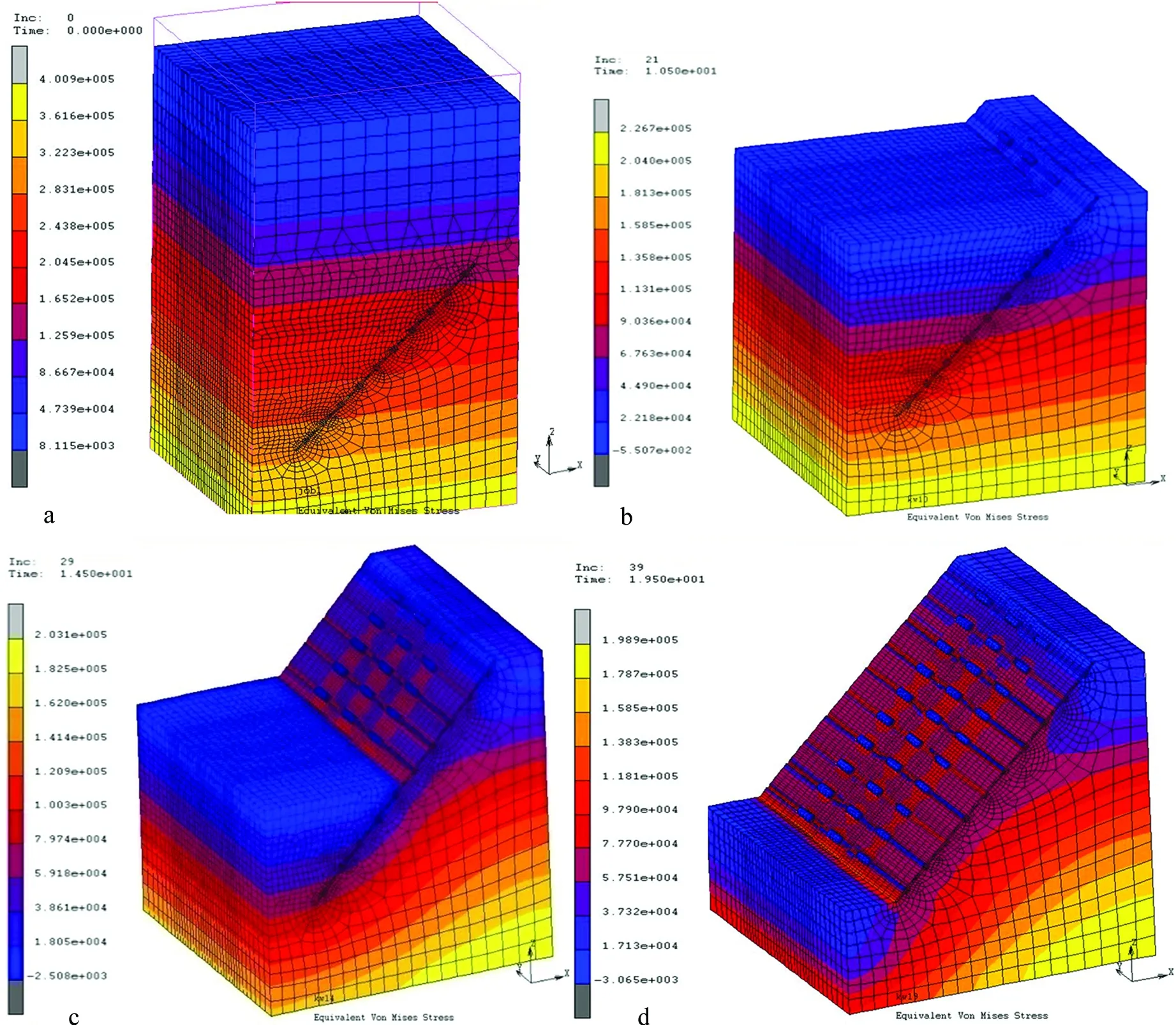
a—开挖前;b—开挖深度为11m；c—开挖深度为15m；d—开挖深度为19m图2 开挖过程中的等效应力变化图

由图3各图形中四条曲线的变化规律可以看出，随着开挖深度的增加，化石和围岩的等效应力都相应减小，且由其变化速率可见，开挖后裸露程度不同的化石应力释放速率相差不大。当开挖到化石所在深度时，不同裸露程度的化石都出现了等效应力维持某一值不变或少许增加或减小、速率降低的现象，而围岩大部分出现了等效应力回弹的现象[10-11]。这些现象都是由于开挖过程中的应力释放及化石和围岩的相互作用而产生的。

对比图3中的四组图形的变化规律，可以看出，埋深深度越大的化石，在开挖露出地面后等效应力的回弹现象越明显，即应力释放越严重。不同深度的围岩随开挖过程的进行，应力变化过程也有较大变化。所以埋深深度对化石的风化是有一定影响的。由数值模拟的结果可以推测，埋深越大的化石，开挖过程中的应力释放对其风化的影响越大。

a—埋深11m;b—埋深14m；c—埋深17m；d—埋深20m图3 不同埋深条件下裸露体积不同的化石及围岩开 挖过程等效应力变化曲线

(2)SXZ变化过程

图4为开挖过程中XZ方向应力的变化过程：随着化石开挖深度的增加，XZ方向剪应力变化情况，由图可见，裸露化石表面大部分受剪拉应力的作用，最大拉应力达到0.3MPa。岩石的抗拉强度要远小于其抗压强度，所以，虽然化石表面所受剪应力不大，但其对化石风化的影响比压应力要大的多。开挖过程中恐龙化石表面的剪拉应力是导致卸载裂隙产生的主要原因。

a—开挖前;b—开挖深度为14m；c—开挖深度为15m；d—开 挖深度为19m图4 随着开挖深度的增加SXZ变化过程

3 化石发掘过程中应变变化分析

这里所分析的应变是与Von Mises等效应力相对应的等效应变[12-14]。化石发掘过程中，由于初始地应力释放，不但导致化石和围岩内部应力的变化，也会产生位移的变化，图5中给出了化石开挖过程中部分开挖阶段的等效弹性应变的变化过程图。随着化石发掘过程中开挖深度越来越大，弹性应变不断发生变化，开挖后最大应变达到10-4，而且化石和其周围围岩的弹性应变并不相同，部分地区相差近1个数量级。故由于开挖深度的增加，不但会使化石和围岩的裸露部分由于应力释放而产生较大应变，而且由于化石和围岩的力学参数不同，还会导致化石和围岩之间由于变形不同而产生力的相互作用[15-16]。

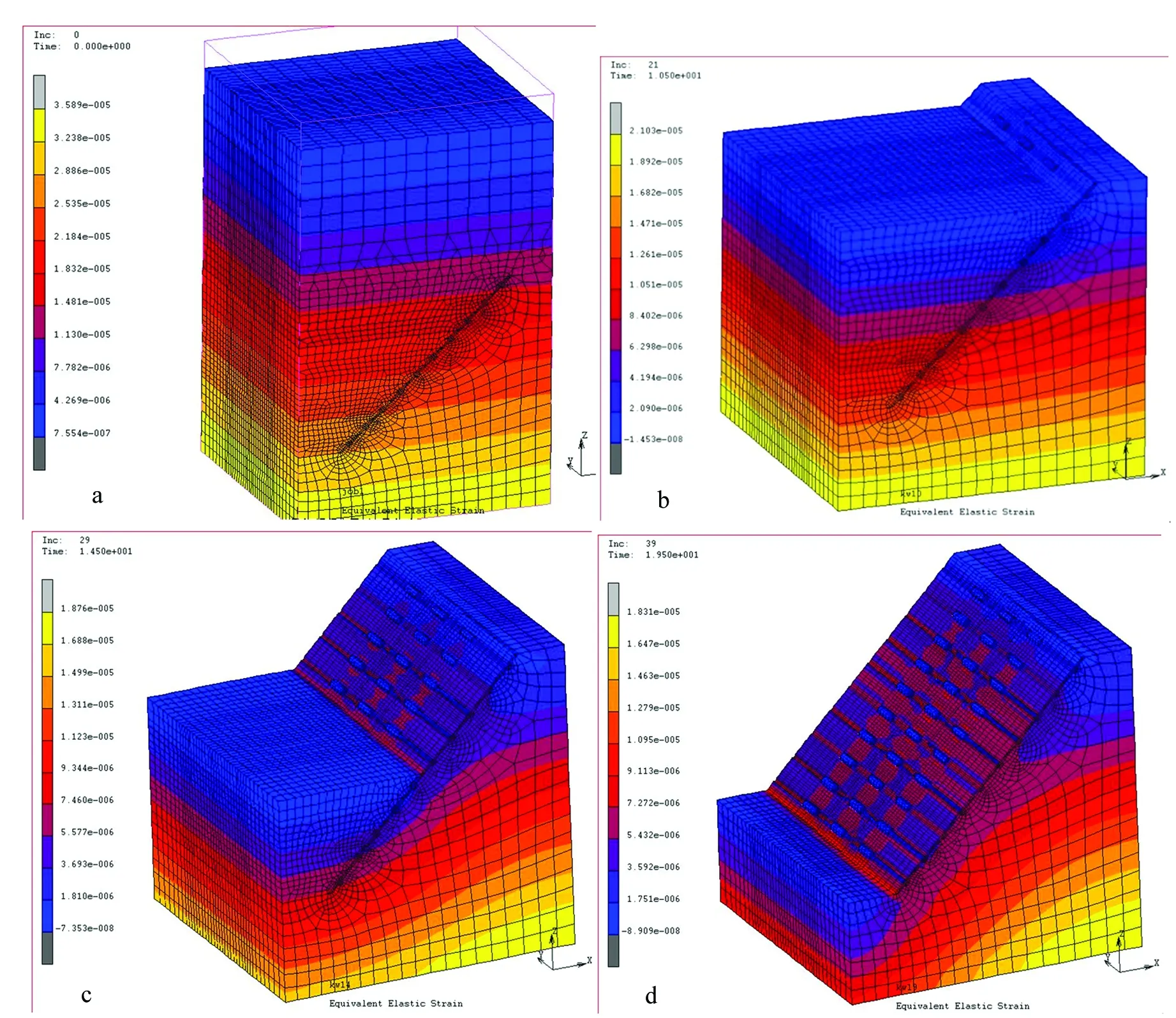
a—开挖前;b—开挖深度为11m；c—开挖深度为15m；d—开 挖深度为19m图5 开挖过程中的等效弹性应变变化

图6给出了不同埋深，相同裸露程度的化石表面位移变化情况，从中明显可以看出，各条曲线起点处为初始未开挖状态，位移越大则表示初始埋深越大。对比各曲线的斜率可以得出，埋深越大，位移初始阶段变化速率越大，当埋深为20m时，位移变化率为2.9×10-4m/开挖步，而埋深为11m时，位移变化率为1.3×10-4m/开挖步，故埋深越大受开挖的影响就越大。

图6 不同埋深条件下相同裸露程度化石的时间位移曲线

4 结论

根据对化石开挖过程的数值模拟，可以得出如下结论：化石开挖过程中应力应变的变化是影响化石风化的重要因素；化石初始埋深越大、开挖速度越快，开挖过程中受应力释放作用的影响也就越大；化石和围岩力学参数的相差程度大小，也会在开挖过程中间接影响化石和围岩的风化；虽然化石表面所受剪应力不大，但其对化石风化的影响比在压应力条件下要大的多，这是导致化石卸载裂隙产生以致破坏的主要原因。因此，恐龙化石发掘要逐层缓慢开挖，使化石逐渐达到新的应力平衡，以便减少应力释放对化石造成的风化破坏，特别是在化石发掘施工中要做好护坡，最大限度地防止剪应力的产生。