恐龙化石在风化破坏过程中内部裂隙扩展的试验模拟研究

张尚坤,于学峰，贾超，杜圣贤，田京祥，宋香锁，陈文芳

(1.山东省地质科学研究院，国土资源部金矿成矿过程与资源利用重点实验室，山东省金属矿产成矿地质过程与资源利用重点实验室，山东 济南 250013;2.山东大学土建与水利学院，山东 济南 250013)

0 引言

恐龙化石由多种矿物成分构成，质地不均匀，在漫长的地质变迁过程中必然受到各种物理化学因素影响而会产生裂隙、孔洞(图1)[1-3]。在研究恐龙化石受力作用下裂隙扩展致使化石破坏试验时，应考虑实验对象的特殊性：①恐龙化石含有杂质较多，成分比较不均匀，而各种成分矿物本身的力学性质差别较大，具有较多的不确定性，其对恐龙化石裂隙的开裂破坏影响比较大。因此，数值计算中用单一均匀的材料模拟试件的加载破坏并不恰当；②从恐龙化石破坏特征可以发现恐龙化石为脆性材料，其破坏呈现弹脆性，用一般的弹塑性模型很难得出符合恐龙化石实际的结果。

自20世纪20年代起，国内外众多学者对脆性材料裂隙扩展做了大量试验研究，Griffith[4]首先对玻璃和陶瓷等脆性材料进行了试验研究，提出了固体强度与裂隙长度之间的关系式。20世纪50年代，Irwin提出了应力强度因子的概念。此后，Hoek，Cook，Mc Clintock，Salamon等学者对脆性材料在单向受压情况下裂隙的扩展进行了更加深入的理论和应用研究[5-13]。20世纪60年代，Brace[14-15]提出了延性开裂机理的二维裂隙滑移开裂模型，该模型适合于解释岩石微裂纹的前期扩展。从20世纪70年代起，许多学者开始在二维条件下对裂隙岩体的开裂、扩展和破裂全过程进行试验研究。Wong T.F.[16-17]等对花岗岩的微观破坏机制进行了系统观测。Nolen-Hoeksema等[18]对大理岩斜裂隙尖端的受压扩展模式进行了试验。自20世纪80年代以来，对脆性材料裂隙的缺陷更加注重理论方面的研究，建立了多个理论模型。通过研究多组雁行排列张性裂隙的开裂、扩展和贯通机制，建立了自由面与多裂隙相互作用的理论模型。20世纪90年代至今，随着新的试验方法的涌现，对脆性材料裂隙缺陷的研究更加深入，采用不同模型对裂隙缺陷的扩展贯通机制、岩桥贯穿机制及失稳模式进行了深入研究。在单轴压缩试验条件下通过对含两个张性裂隙的石膏试样的裂隙贯通实验，发现平行的初始预制裂隙缺陷的几何分布控制着裂隙体的贯通机制。项吕等[19-21]通过雁形裂隙双向加载的相似材料模型试验，提出了断续节理裂隙蠕变演化的等效模型以及考虑节理裂隙扩展-损伤耦合的本构方程。

图1 恐龙化石裂隙示意图

在综合前人试验和理论模型的研究成果的基础上，运用数值分析方法对内含裂隙恐龙化石的断裂破坏过程进行模拟研究。在FLAC3D中采用FISH语言编写了基于体元分析的计算程序，采用弹脆性本构模型，分析试验过程中裂纹萌生→扩展→贯通规律和裂隙化石的断裂损伤机制。

1 理论背景

随着计算机模拟技术的突飞猛进，运用数值分析的方法模拟材料的裂隙损伤断裂问题，已经得到了各界的认可和广泛应用。FLAC3D(Three Dimensional Fast Lagrangian Analysis of Continua)是美国Itasca Consulting Group Inc.开发的三维快速拉格朗日分析程序，该程序能较好地模拟地质材料在达到强度极限或屈服极限时发生的破坏或塑性流动的力学行为，特别适用于分析渐进破坏和失稳以及模拟大变形[22-23]。

目前，弹脆性损伤模型已广泛应用于混凝土、陶瓷、岩石、石膏和某些脆性或准脆性金属材料[24-28]的损伤断裂数值分析。恐龙化石的力学性质与混凝土、岩石、石膏等脆性材料极具相似性，在载荷作用下会形成损伤，这样的损伤导致恐龙化石内部结构不断变化、性质不断弱化，最终导致化石破坏，这基本符合脆性材料的破坏特点。所以，采用弹脆性损伤模型对恐龙化石的断裂力学分析计算过程进行模拟，可以很好地描述恐龙化石内部裂隙的演变规律。因此，采用弹脆性损伤力学本构关系描述恐龙化石的力学特性是合适的。

根据应变等价原理，可得到损伤恐龙化石材料的应力-应变关系如下：

(1)

式中：E0和E分别为初始弹性模量和损伤弹性模量；σe为有效应力；D为损伤变量，范围在[0,1]之间。D=0对应于无损伤状态，0﹤D﹤1对应于不同的损伤程度。当D=1时，对应于单元体完全处于断裂状态。为避免有限差分法的应力-应变计算中出现零值而导致数学错误，参照项吕等研究裂隙岩体断裂的做法，将断裂后单元参数用一个远小于原始参数的数值代替[19-21]。

带有残余强度的弹脆性模型在单轴拉伸应力作用下的损伤演化方程为:

(2)

式中：σi=η·σt,σi为残余强度；εt0为初始损伤阈值；εtu为极限拉伸应变；η为残余强度系数。

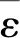
(3)

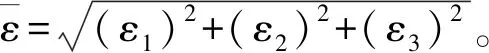
由此，可以得到损伤恐龙化石的应力应变关系的损伤本构方程：

(4)

进而可以推导出剪切应力条件下的损伤演变方程：

(5)

式中：εc0为剪切损伤应变阈值，σrc为剪切损伤残余强度；

剪切损伤单元的应力应变关系式如下：

(6)

2 数值试验研究

2.1 数值模拟进程图

参照项吕等研究裂隙岩体数值模拟进程图[19-21]，制定模拟恐龙化石的弹脆性损伤应变进程图，如图2。

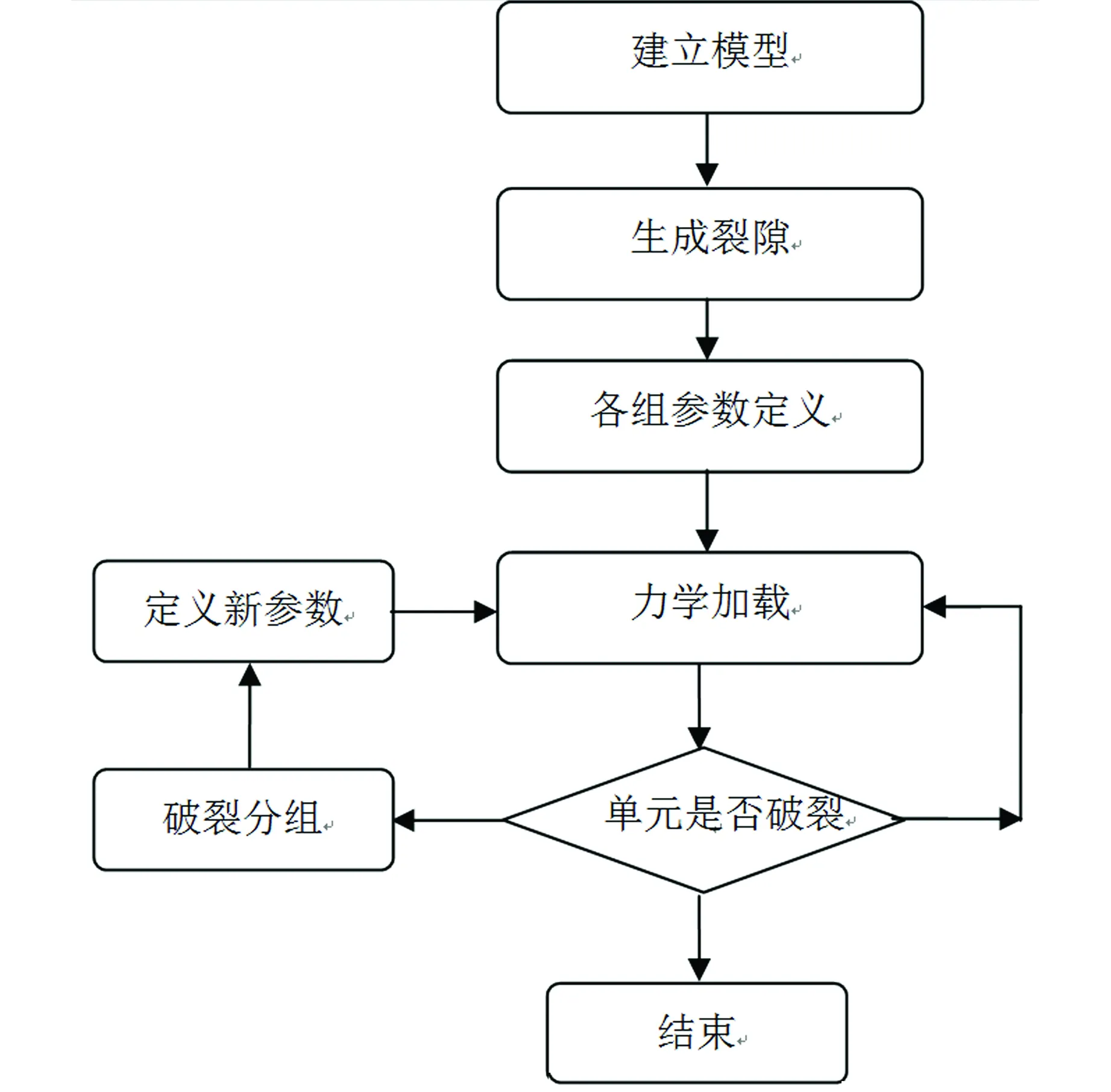
图2 模拟恐龙化石的弹脆性损伤应变进程图

2.2 计算模型及参数

将计算模型尺寸设定为：80mm×150mm×1.5mm。单元尺寸设置为1mm3左右，用六面体单元自由划分，约划分为18000个单元，将其分成原岩组、弱单元组和原生裂隙组三个介质组。随机选择5%的单元体赋为弱单元组，以模拟原岩中随机存在的缺陷；设置2个倾角为45°的原生裂隙(20mm×1.5mm)平行分布于模型中央，2个原生裂隙组间距为20mm，计算模型如图3所示。三个组别中单元体的泊松比、弹性模量、抗拉强度、粘结力等参数见表1。

图3 FLAC模型结构图

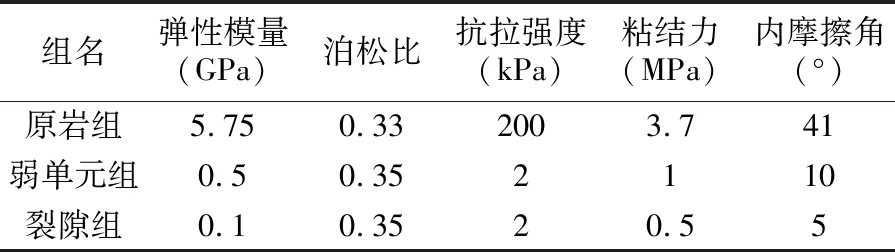
组名弹性模量(GPa)泊松比抗拉强度(kPa)粘结力(MPa)内摩擦角(°)原岩组5.750.332003.741弱单元组0.50.352110裂隙组0.10.3520.55

恐龙化石的几何形状、密度、矿物排列方向、边界约束、外荷载等在自然状态下呈各向异性。在化石断裂过程中，这种状况导致了应力和应变的非均匀分布，这对裂纹扩展模式和扩展强度都有很大影响。在计算模型中，化石被划分成体积为1mm3的若干微小块体单元，由于块体单元体积很小，从微观的角度来看，它们之间是连续均匀的。但由于恐龙化石自身和边界呈现的各向异性，使这些块体之间必定存在着力学属性差异，这个差异尽管很小，但在宏观上就会表现为材料的非均匀性，即化石材料的内部缺陷。在数值分析模拟时，通常用弱单元来描述化石内部缺陷。当对恐龙化石模拟施加单轴压力时，代表缺陷的弱单元首先达到峰值强度，而其它单元则仍处于峰值前的硬化阶段；当应力超过化石的强度阈值时，代表缺陷的弱单元立即进入软化阶段，而弱单元附近的其他原岩组单元随之通过卸载来保持整体应力的连续性。

3 试验结果与分析

3.1 单轴压缩作用下的应力-应变过程

通过对含有原生裂隙和无原生裂隙恐龙化石试件在单轴压缩作用下的轴向应力-应变关系(图4)可以看出：初始阶段(A-B)应力与应变成正相关，为线弹性阶段；随着应力增加，应变与之的相关性减弱(B-C)，应变进入非线性变形阶段；当应力超过化石的抗拉强度阈值后，化石材料迅速进入软化阶段(C-D)。各阶段的裂隙扩展状况如图4所示。

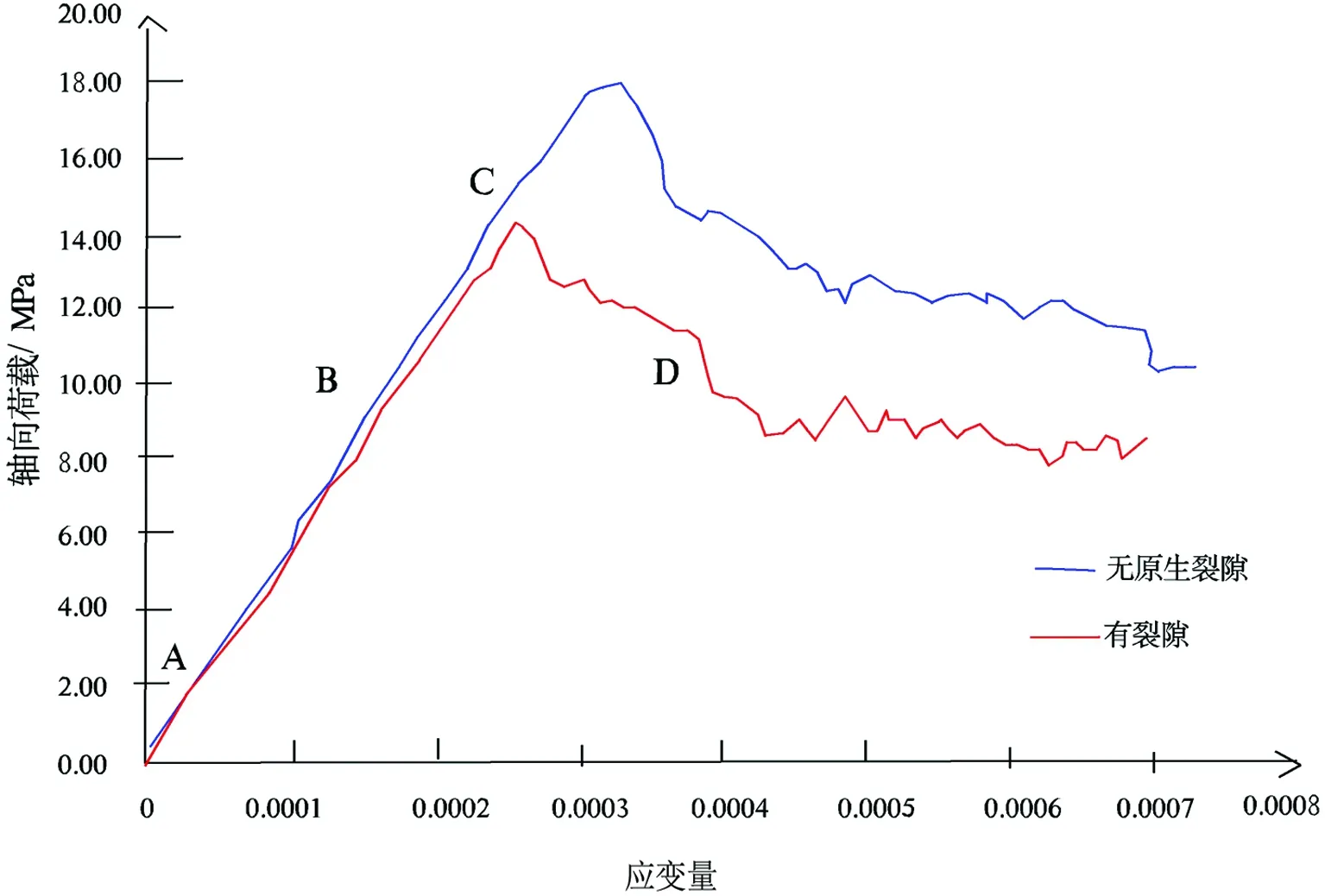
图4 有无裂隙作用下应力(轴向)-应变(轴向)曲线

以下为针对含有裂隙的恐龙化石试件的破坏过程分析。

(1)线性变形阶段(图4，A-B段所示)：在初始加载阶段，以张拉性破坏为主，原生裂隙靠近上下边界的端部首先产生翼裂纹，同时，在弱单元分布的区域零星出现破坏点。随着加载的持续进行，原生裂隙的另一端也逐渐萌生出翼裂纹，这些翼裂纹沿上下方向扩展增大，此时，试件中的破坏点明显增多，分布在原生裂隙延展方向的试件端部的个别破坏点也逐步扩展为细小的次生裂纹，但次生裂纹之间岩桥完整，裂纹没有贯通。从A点到B点的裂纹扩展状况(图5，a～d)总体较简单，其应力-应变行为表现出较好的线性特征。

(2)非线性变形阶段(图4，B-C段所示)：随着载荷的增加，应变进入非线性阶段，当应力达到14 MPa时，化石试件的应变达到峰值强度(0.25×10-3)，即图4的C点位置。在非线性变形阶段，翼裂纹首先扩展并逐渐与原生裂隙贯通，分布于化石试件右上角和左下角的由破坏点发展起来的次生裂也进一步扩展(图5，e～g)，并最终与原生裂隙的翼裂纹贯通，与此同时，试件新产生出多条与原生裂隙的翼裂纹平行的次生裂隙，这些次生裂隙随着载荷增加会迅速发展，并逐渐汇集、相互贯通成网格状。在该阶段，裂纹的扩展方式十分复杂，宏观应力场的分布也随裂纹的扩展而发生变化；裂纹的边界粗糙，呈断续的折线形态，应力-应变曲线呈现明显的非线性(图4)。当载荷超过应变峰值强度后，化石内部将生成大量新的诱导裂隙，导致化石内部结构发生剧烈变化，变形进入软化阶段。

(3)软化阶段(图4，C-D段所示)：C点之后，内含裂隙的化石和不含裂隙的化石的应力强度明显发生分化，内含裂隙的化石应力迅速从14MPa降低到8.0MPa，而不含裂隙的化石应力则继续增大至18MPa后，才迅速下降至10MPa，这充分说明化石的内部裂隙严重影响化石强度。从图5h可以看出，进入软化阶段，无论是原生裂隙还是次生裂隙(或诱导裂隙)均迅速扩展，其宽度、深度、长度都有所加大。该阶段化石虽然仍有一定的残余强度，但化石内部遭受破坏的单元数目迅速增长，其结构随着裂隙逐渐扩展连通而发生显著变化。

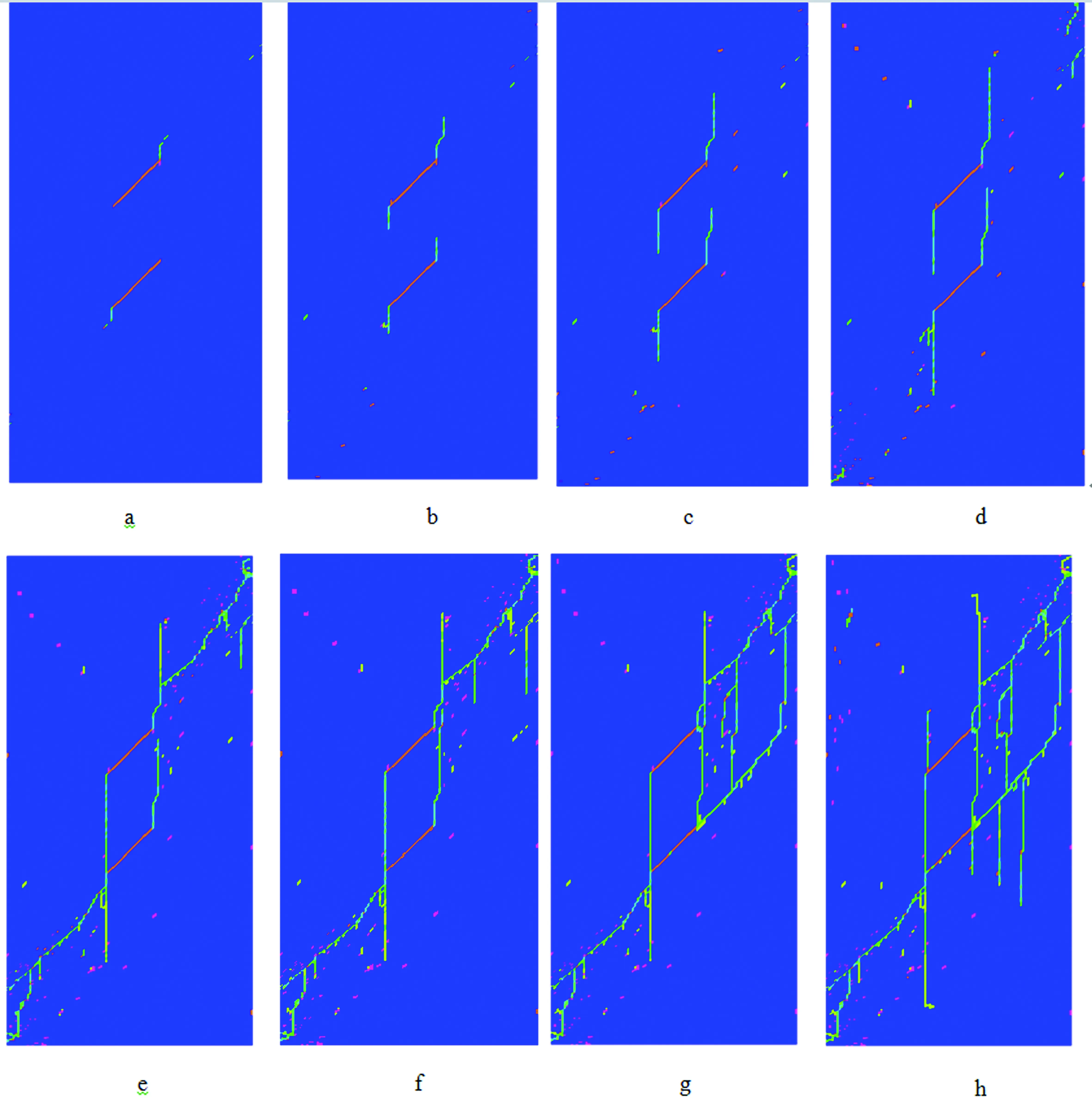
图5 有裂隙裂纹扩展过程

3.2 单轴压缩作用下裂隙块体的体积应变、纵向应变、横向应变规律

通过对有、无裂隙的化石试件单轴压缩试验，记录模拟过程的横向应变和轴向应变，进而求得体积应变，并绘制出两种方案应力-体积应变曲线(图6、图7)。从两种方案的应力-体积应变曲线可以看出，达到应力峰值时，无原生裂隙的化石试件体积应变量明显大于内含原生裂隙的化石试件。并且有裂隙的情况下，因受化石内部裂隙逐渐扩展延深的影响，化石的体积应变在达到峰值强度后变得较为紊乱。

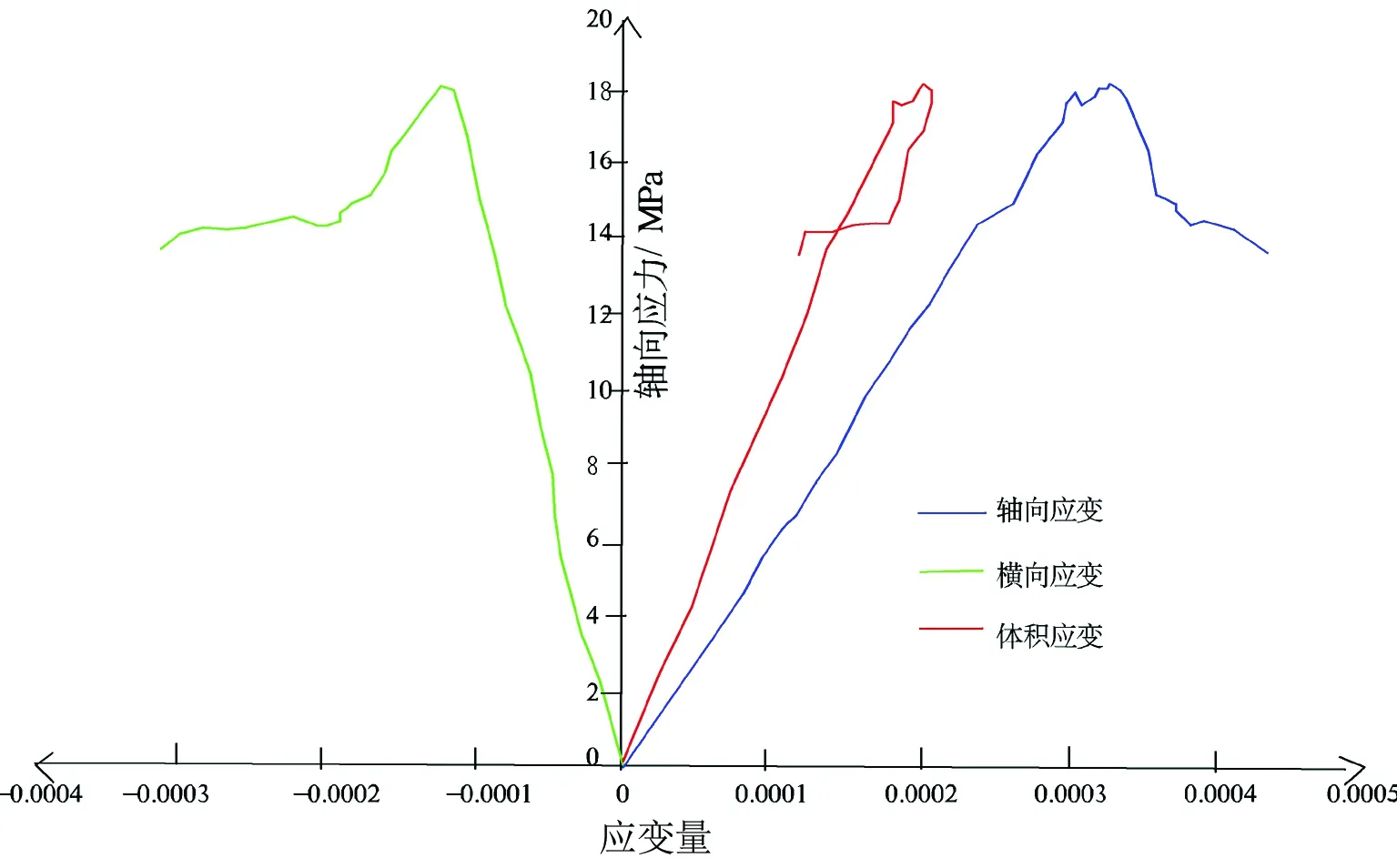
图6 无裂隙应力-应变曲线

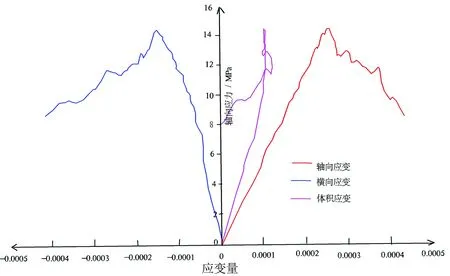
图7 有裂隙应力-应变曲线

3.3 单轴压缩作用下有无原生裂隙块体的破坏情况分析

图8为原生裂隙试件，在单轴压缩条件下的破坏情况分析，如图可以看出，没有裂隙情况下，单轴破坏试验显示，其裂隙扩展是沿对角近似呈直线状扩展延深，直至破坏。含有裂隙情况下的单轴破坏试验，裂隙扩展主要沿原有裂隙扩展，裂隙扩展纵横交错，较为复杂，最后沿阶梯型裂隙破坏。

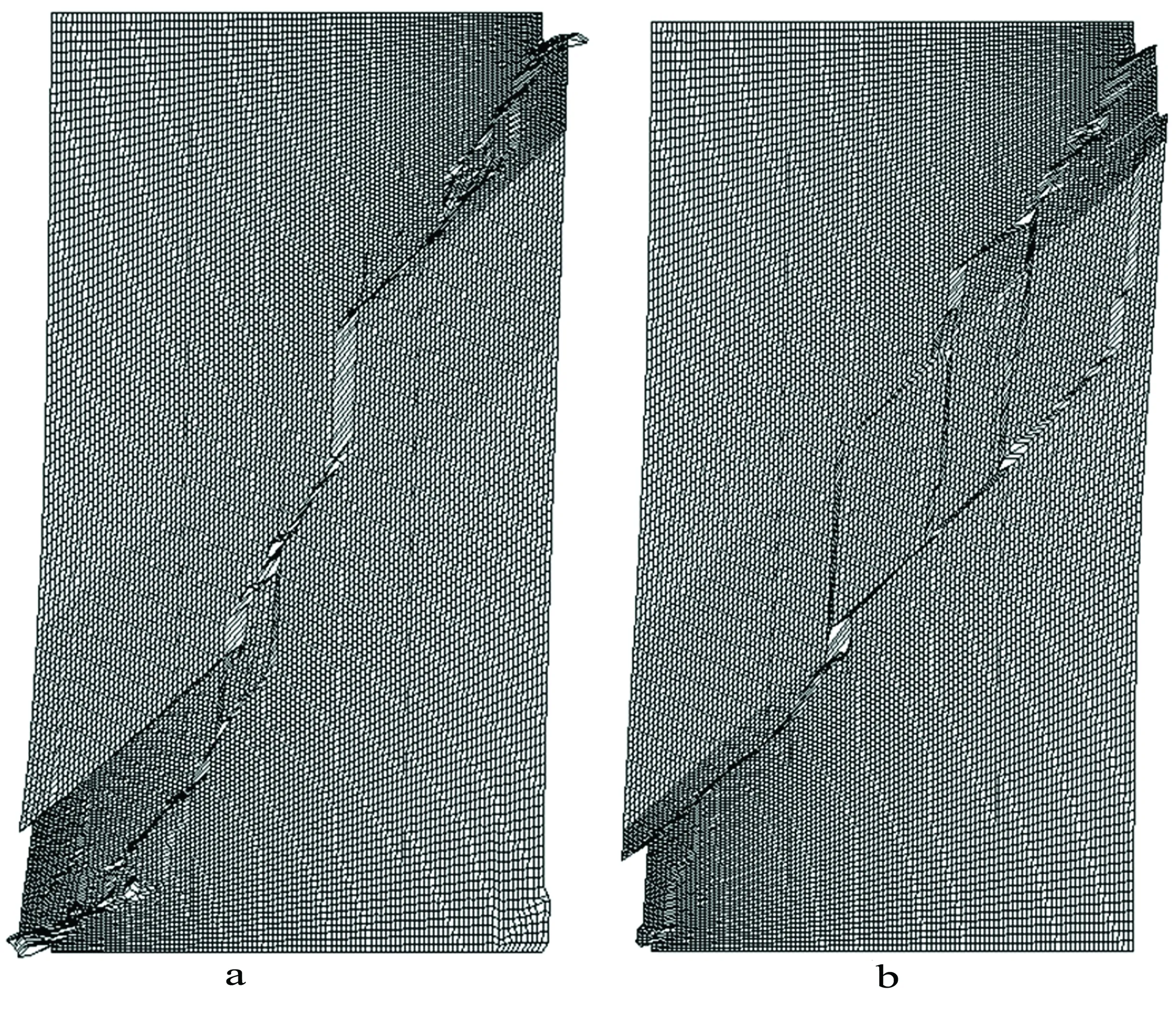
a—无裂隙试件；b—有裂隙试件图8 不同试件显示的破坏情况

4 结论

(1)有裂隙恐龙化石的抗压强度值比无裂隙恐龙化石的抗压强度值小30%，最终的残余抗压强度也略小。因此恐龙化石如果存在原生裂隙，其整体的强度会大大降低，容易被破坏，需要特别予以保护。

(2)内含裂隙的恐龙化石在外力破坏前，其破坏单元较分散，破坏后宏观主破裂面则变得更为复杂，倾角较陡，表面较宽且粗糙。而无裂隙恐龙化石在外力加载至接近破坏点时，出现的破坏单元则更集中。因此，在加载应力作用下，相比不含内部裂隙的恐龙化石，内含裂隙的恐龙化石其内部裂隙会迅速大量扩展，加重风化程度和破坏速度。

(3)值得注意的是，恐龙化石峰后的强度软化过程非常不稳定，峰值附近的材料力学行为对化石试件内部缺陷的分布十分敏感。因此，恐龙化石如受频繁应力变化，容易造成次生裂隙，会加快风化破坏速度。