含电动汽车的区域综合能源系统日前调度优化

(四川大学电气工程学院，四川 成都 610065)

0 引 言

为解决化石能源日益枯竭以及人类对能源需求日益增长的问题，各国大力发展具有清洁、易于获取、资源覆盖面广等特点的可再生能源[1]。在此基础上，优化能源结构，从化石能源结构向可再生能源结构转型成为必然趋势。为提高用能效率并综合协调管理，能源互联网应运而生。与传统的单一微电网系统相较，区域综合能源系统[2-7]将中低压配电网、配气网、冷/热网等不同形式的网络进行紧密耦合，不同能源间高效的互补互济提高了系统整体调度灵活性。但多能协调管理和转化机制也会带来新的挑战。

目前，在区域综合能源系统调度层面已有许多研究。文献[8]针对区域综合能源系统面临灾害的弹性恢复能力和系统运行经济性之间的矛盾问题,提出多目标加权模糊规划的优化方法。文献[9]针对含电转气技术的综合能源系统，面向供给侧储能/储气设备和需求侧暖通空调等，提出了一种基于李雅普诺夫的事件触发型在线能量优化方法。文献[10]针对冷热负荷存在惯性，提出多元储能技术，构成多元储能系统对区域综合能源系统进行优化。上述文献从不同方面考虑了如何对区域综合能源系统进行优化并相应提出优化方法；但针对的都是传统的电气元件进行建模优化仿真，缺乏针对迅速普及的电动汽车[11-12]对区域综合能源系统优化运行影响的研究。

下面针对此问题，将电动汽车视为园区内可调度的调峰资源，建立了一种含电动汽车和多种分布式电源[13]的热电联供[14-16]的区域综合能源优化模型，并使用具有求解线性规划问题功能的Python进行仿真求解。

1 区域综合能源系统模型

1.1 模型设定

设定区域综合能源系统具有一个可以对电动汽车进行有效调度运行的EV聚合商、风光分布式电源、微型燃气发电设备、锅炉以及外部接入的电网等，如图1所示。通过先进的物联网、通信技术将上述系统组成联系到一起，配合各类储能设备以及电动汽车的辅助，使不同种类能源互补互济、优化运行，提高能源利用率以及清洁能源的使用量，同时使购买能源的费用达到最低。

图1 系统模型

1.2 目标函数

建立区域综合能源系统优化模型的目的是通过能源之间的协调运作，降低能源的使用成本(购电购气成本减去区域内发电并网收入)，提高经济性。以此为目的建立如下目标函数。

C=min(Ce+Cgas+CEV)

(1)

1.3 系统模型

1)微型燃气轮机机组模型

(2)

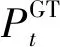
2)燃气锅炉模型

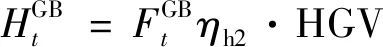
(3)

3)吸收式制冷机组模型

Qchi,t=Hc,t·ηc

(4)

式中：Hc,t和Qc,t分别为第t个时段吸收式制冷机的输入热功率和输出冷功率；ηc为吸收式制冷机组热转冷效率。

4)电锅炉

(5)

5)电制冷机组模型

QAC,t=PAC,tηAC

(6)

1.4 约束条件

1)电功率平衡约束

Pe.t+Pgas.t+Pclean.t=PLD.t+PEV.t+Ph.t+Pc.t

(7)

式中：Pclean.t为第t个时间段风光分布式电源产生的电能；PLD.t为第t个时间段的区域用户用电负荷(电动汽车负荷除外)；Ph.t为第t个时间段的电锅炉输入电功率；Pc.t为第t个时间段的电制冷机输入电功率。

2)热、冷功率平衡

(8)

3)风光发电约束

0≤Pclean.t≤Pclean.max

(9)

根据区域所在的地理位置与历史风光发电信息对风光分布式电源进行发电预测，预测出每个时间段的发电最大值Pclean.max，各个时刻清洁能源的使用量不能高于Pclean.max。

4)EV约束

考虑到用户用车的习惯，同时电动汽车使用和充电不能同时进行，在用户不使用电动汽车时，将电动汽车当做储能资源使用，EV聚合商相应的给予用户价格补偿或者使用其他激励机制激励用户将电动汽车作为储能资源，EV聚合商在协商好的时间段可以任意对电动汽车进行充放电操作。

(10)

式中：β为单位时间电动汽车储能电池充入或放出的最大电能；W为电动汽车的日最大充放电容量。在第t个时间段内存储的能量与前面储存的能量累加值不能超出电动汽车存储的最大限度或者为负值，同时每个时间段充放的电能也不能超过单位时间所能充入的能量最大值。

2 算例分析

2.1 算例描述

选某一区域综合能源系统为研究对象，图2为某区域夏季某一日的电负荷、热负荷、冷负荷以及风光功率预测曲线。

本算例中存在电转热、电转冷、气转电、气转热等能量转化过程，具体能量转化效率如表1所示。

本算例中，电网电价高峰时段为7:00—11:00、19:00—23:00，低谷时段为23:00至次日7:00，平段为11:00—19:00。该区域内平段电价为0.6元/kWh，按照峰谷分时浮动电价以高峰时段上调50%，低谷时段下降50%标准，高峰时段该区域电价0.9元/kWh，低谷时段该区域电价0.4元/kWh。

图2 夏季某日负荷曲线

表1 能量转化效率

天然气按照2元/m3计算，1 m3天然气与10 kWh电的能量相等，同时按照各种能量的转化效率，定制以下发电、制冷、制热成本：

根据各种类型产生能量的成本大小，基于成本最低的目的，规定只考虑利用余热制冷，而不进行锅炉燃气只用于制冷的运行；其次，考虑到平段谷段电网电价较低，所以平段谷段不使用锅炉产热。除此之外，为电动汽车用户提供的价格补偿为每充放1 kWh电补偿0.4元，清洁能源发电成本为0。在此基础上，鉴于本算例的电网电价机制，电动汽车在电网电价谷段充电，在平段不参与充放电，而在峰段放电，使清洁能源全部投入使用。

本算例中电动汽车储存能量在时刻1的初始值设为0，每个小时的最大充放电量为2 MWh。

2.2 算例仿真

基于以上的算例说明使用Python对模型进行优化仿真并求解。仿真结果见图3至图5。

如图3所示，在电价低谷时间段内，系统从电网获取大量电能。随着时间的推移，电价升高，电能的供应形式从电网供电慢慢过渡到由燃气轮机进行供电。除此之外，从图中电动汽车的充放电情况中可以看出，电动汽车在低谷时段充电、用电高峰期放电，不仅降低用电成本，而且参与调峰，同时为电动汽车用户带来经济效益。

图3 优化后电功率负荷供给来源曲线

图4中分别为燃气余热供热功率随时间变化仿真曲线、电能转化的热能功率随时间变化仿真曲线、锅炉产生的热功率随时间变化仿真曲线。

图4 优化后热功率负荷供给来源曲线

如图4所示，燃气轮机除了在平段和峰段产生电能，还同时利用余热产生大量热能满足热负荷需求。在仿真图中可以看到，当夏季热负荷需求较少时，余热可以供应大部分热负荷。其余部分的热负荷，在谷段由电能转化为热能，在用电高峰段由锅炉产热供应热负荷。

图5中给出了吸收式制冷机组利用燃气余热和锅炉产生的余热制冷功率随时间变化仿真曲线、电能转化为冷功率随时间变化仿真曲线。

如图5所示，吸收式制冷机组在谷段和平段吸收余热提供大量冷能，显著地实现了能量的梯级利用。其余冷能几乎由平段和谷段的低电价电网电能提供。

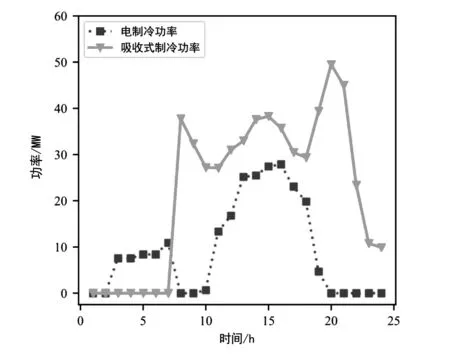
图5 优化后冷功率负荷供给来源曲线

2.3 对比分析

为进一步研究电动汽车在区域综合能源系统起到的优化作用，改变系统中的可用于充当储能资源的电动汽车数量和每个小时的充放电量，并进行仿真对比分析。

将电动汽车每个小时的最大充放电量从0分别提高到5 MWh、10 MWh、20 MWh、25 MWh,电动汽车充放电随时间变化仿真曲线如图6所示。燃气轮机发电量随时间变化仿真曲线如图7所示。

图6 电动汽车充放电功率

如图6和图7可以看出，随着电动汽车每个小时的最大充放电量不断提高，电动汽车在谷价时段的实际充电量也相应提高，并在高峰时段放出，替代相对成本更高的燃气轮机。

对不同充放电量约束条件(假设有足够的电动汽车)下的系统运行总成本进行仿真计算，结果如表2所示。

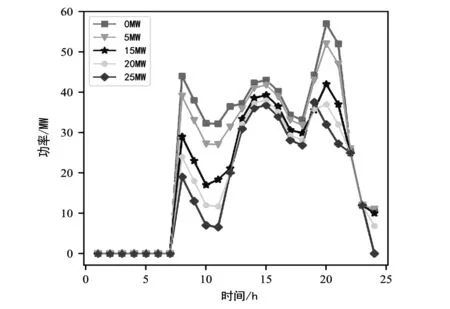
图7 燃气轮机发电功率

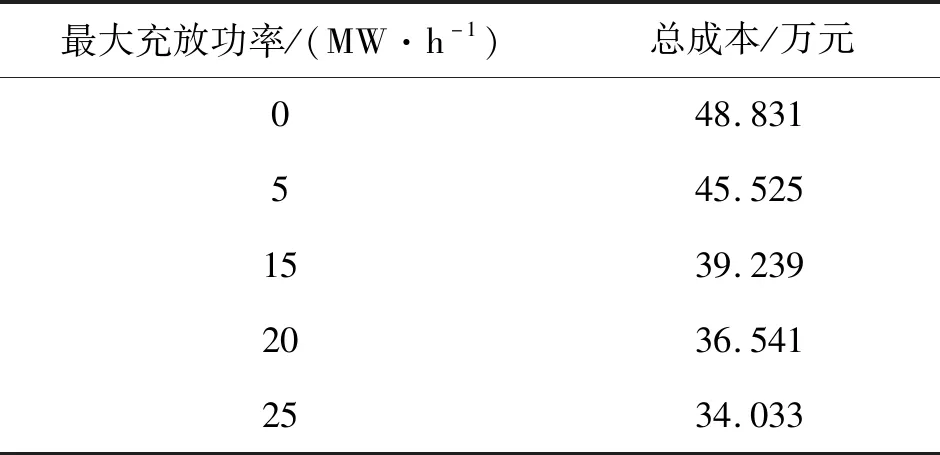
表2 仿真数据

如表2所示，当每个小时电动汽车的最大充放量变大并且有足够的电动汽车可供调用时，系统使用能量的总成本不断下降，经济性不断提高。

3 结 语

以系统能源成本为目标建立了含有电动汽车的区域综合能源系统模型。仿真结果表明：

1)基于区域内的负荷特性对电网电能、天然气、清洁能源发电的使用进行优化，有效消纳了区域内风光能源；冷热电的梯级利用，大幅提高了能源利用率；通过对天然气与电网电能的交替配合使用既满足能源需求、有效调峰，又达到成本最小化的经济效果。

2)随着可控的电动汽车数量变多、EV聚合商的规模变大，能将其作为调度资源参与调峰并降低成本。系统不需要额外的建设费用，同时电动汽车用户也可以得到相应的经济收入，相较于高成本的储能蓄电池，其潜力更大。