基于EMD的金刚石砂轮磨损状态声发射监测

郭力 霍可可 郭君涛

摘    要：针对磨削金刚石砂轮磨损状态声发射信号小波分析中存在的问题，根据工程陶瓷部分稳定氧化锆磨削过程中声发射信号非线性非平稳性的特点，采用经验模态分解方法将磨削声发射信号分解为多个平稳的固有模态函数之和，并提取其有效值、方差和能量系数等特征值.在磨削金刚石砂轮从轻度磨损状态转变为严重磨损状态时，固有模态函数的有效值（IMFrms）和方差（IMFvar）增大，而能量系数（IMFpe）发生明显的变化;将其做为最小二乘支持向量机的输入参数，对金刚石砂轮的轻度磨损状态和严重磨损状态成功地进行了智能监测.

关键词：氧化锆磨削;金刚石砂轮磨损状态监测;声发射;经验模态分解;最小二乘支持向量机

中图分类号：TG58，TP183                       文献标志码：A

Acoustic Emission Intelligent Monitoring of Diamond Grinding

Wheel Wear Based on Empirical Mode Decomposition

GUO Li？覮 ，HUO Keke，GUO Juntao

（College of Mechanical and Vehicle Engineering， Hunan University， Changsha 410082，China）

Abstract： In view of the existing problem in the wavelet analysis of acoustic emission signals in wear state of diamond grinding wheel， because engineering ceramics partially stabilized zirconia grinding acoustic emission signals have nonlinear and nonstationary characteristics， using empirical mode decomposition method the acoustic emission signals were decomposed into several stationary intrinsic mode functions and then the root mean squares， variances and energy coefficients were extracted. When the wear state of diamond grinding wheel changes from mild wear to severe wear， the root mean squares（IMFrms） and variances（IMFvar） of the intrinsic mode function increase， and the energy coefficients（IMFpe） change significantly. As the input parameter of the least squares support vector machine， the wear state of diamond grinding wheel was successfully monitored.

Key words： partially stabilized zirconia grinding;diamond grinding wheel wear state monitoring;acoustic emission;empirical mode decomposition;least squares support vector machine

工程陶瓷部分穩定氧化锆PSZ以高耐磨性、耐高温、高硬度、耐腐蚀、绝缘和不导热等优异性能，在航空航天和电子、化学、机械工业等重要领域的应用越来越广泛.一般工程陶瓷要精密加工后才能使用，要用金刚石砂轮来磨削工程陶瓷，由于工程陶瓷是硬脆难加工材料，使昂贵的金刚石砂轮磨削中容易产生磨损导致磨削力磨削温度增大，磨削去除率和磨削质量下降，导致磨削加工费用上升.为了准确地预测金刚石砂轮的磨损状态，以便及时修整砂轮，提高金刚石砂轮的利用率，降低金刚石砂轮的损耗，提高工程陶瓷的磨削质量，有必要在陶瓷磨削加工中对金刚石砂轮的磨损状态进行监测.金刚石砂轮磨损状态测量难以采用直接方法，即便用直接法测量会导致磨削过程中断.而声发射（acoustic emission，AE）等非接触间接监测砂轮磨损减少了停机时间和成本，提高砂轮寿命和磨削质量，又不依赖磨床操作者的技能，是智能制造监测的主要的研究方向;它包括磨削AE信号采集与处理、特征提取与智能决策.

文献[1]应用经验模态分解（Empirical Mode Decomposition， EMD）将车削加工声发射信号分解为几个固有模态函数（Intrinsic Mode Function， IMF），再提取IMF分量的归一化能量值并将其作为特征向量，应用最小二乘支持向量机LS-SVM对车刀磨损状态成功地进行识别.文献[2]对陶瓷磨削砂轮磨损进行了声发射智能监测，应用了自适应神经模糊推理系统、多层感知器神经网络、径向基函数神经网络和广义回归神经网络等几种先进的方法，砂轮小切深条件下砂轮磨损分类准确率达90%以上.文献[3]应用总体经验模态分解 EEMD得到无模态混叠的固有模态函数IMF分量，再应用相应的算法从所有IMF分量中提取敏感的IMF;提取敏感IMF的能量作为支持向量机（SVM）分类器的输入，车刀磨损状态分类预测准确率在93%以上.文献[4]研究了基于声发射信号EMD分解与IMF奇异值熵的车刀磨损状态监测方法，由于锋利车刀的IMF奇异值熵大于磨损车刀的，所以可以用来监测车刀的磨损.文献[5]把经验模态分解EMD应用到磨削烧伤声发射信号的分析中，提出了基于平均能量的固有模态函数IMF分量选择方法.文献[6]认为希尔伯特黄变换（HHT）能够自适应地高效分解信号，反应信号的局部特征，可以分析非线性非平稳振动信号.所提取的铣刀磨损特征固有模态函数IMF3、IMF4、IMF5和IMF6的振幅均值和边际谱中的最大幅值能准确可靠地反应铣刀磨损状态.文献[7]切削声发射信号的频率高，而切削加工中的环境噪声信号频率都比较低，所以声发射信号的抗干扰能力强.切削刀具磨损的声发射信号具有非线性特性，所以采用混沌理论对不同刀具磨损程度的声发射信号进行了分析，分析发现关联维数可作为特征量用于刀具磨损检测.文献[8]发现可以通过使用激光照射试验产生的热声发射信号来训练神经网络，对磨削高温合金的砂轮磨损状态进行监测，有效地减少了磨削实验而节省了费用.文献[9]认为自适应最稀疏时频分析方法在抗噪声性能、抑制端点效应和模态混淆以及提高分量的准确性等方面要优于经验模态分解方法，是信号分析的好方法.文献[10]提出了两种蚁群优化算法和著名序列前向浮动选择法，作为声发射信号特征提取的最优化方法，作为磨削砂轮磨损状态智能监测.

由于小波分解方法只能分析平稳信号，所以使用小波分解方法来准确分析金刚石砂轮磨损声发射信号这种非平稳信号是比较困难的[1].本文结合工程陶瓷部分稳定氧化锆PSZ磨削过程中AE信号非线性非平稳性的特点，采用经验模态分解EMD方法将其AE信号分解为多个平稳的固有模态函数之和，再提取其有效值、方差和能量系数等特征值，将其做为最小二乘支持向量机LS-SVM的输入参数对磨削金刚石砂轮的轻度磨损和严重磨损状态进行智能监测.

1   磨削声发射信号的采集

在一台MGS-250AH精密平面磨床上进行试验，试验中使用青铜结合剂金刚石砂轮粒度为60#、宽度为10 mm、直径为150 mm. 试验中工作台速度不变，砂轮转速固定为1 600 r/min即线速度12 m/s，磨削保持切深为5 μm，即实验中磨削参数保持不变.工程陶瓷部分稳定氧化锆PSZ磨削试件安装在虎钳夹具中，夹具用電磁吸力安装在磨床工作台上，声发射传感器用磁力安装在虎钳工件夹具上尽可能靠近磨削工件.试验不用磨削液，消除了磨削液对磨削声发射信号分析的影响.本试验采用的部分稳定氧化锆PSZ磨削试件尺寸为35 mm×15 mm×10 mm， 磨削在试件35 mm×15 mm的平面内沿15 mm方向进行.PSZ材料密度为5.97 g/cm3; 抗弯强度大于800 MPa; 微观硬度为12.5 GPa;断裂韧性为7.5 MPa·m1/2;弹性模量为205 GPa;PSZ材料扫描电镜照片显示其晶粒尺寸小于1 μm，其中存在一定量的气孔.可见PSZ工程陶瓷是典型的硬脆难加工材料.

PSZ磨削过程产生的AE信号，传播到放在平面磨床工作台夹具上的美国物理声学公司PAC生产的压电AE传感器WSa，经过AE压电连接器的前置放大，再到PAC生产的PCI-2声发射信号采集卡和AEwin采集系统进行信号采集，并输入到计算机进行保存等待MATLAB软件进行后续的处理.为了不失真，AE信号采样频率为2 MHz，前置放大增益为40 dB，门槛为固定40 dB.WSa声发射传感器的工作频率范围在100 ～ 1 000 kHz，谐振频率为125 kHz.

采集金刚石砂轮在轻度磨损和严重磨损[10-11]程度下的多次磨削PSZ声发射信号，每次实验磨削参数相同，即实验中工作台速度不变，砂轮转速固定为1 600 r·min-1即线速度12 m/s，磨削保持切深为5 μm.砂轮轻度磨损实验是采用修整后的金刚石砂轮磨削5次PSZ，此时砂轮磨粒磨刃锋锐，所以用测力仪测量到的法向磨削力增加很小，因而采集到的磨削AE信号可作为砂轮轻度磨损的AE信号.砂轮严重磨损实验是在砂轮轻度磨损的5次PSZ磨削实验结束后继续进行，一直磨削PSZ到20次，砂轮随着磨削次数增加磨损加剧，所以用测力仪测量到的法向磨削力增加明显，采集到的磨削AE信号作为砂轮严重磨损的AE信号.因此实验中每磨削20次对金刚石砂轮进行修整，再进行下次砂轮轻度磨损和严重磨损磨削AE实验，实验中只测量砂轮磨损的磨削AE信号.

2   磨削声发射信号的处理

图1～图2可以看出金刚石砂轮在轻度磨损变到严重磨损时磨削AE原始信号幅值增加，但是AE信号频率主要分布范围没有发生明显的变化，都是主要集中在0～600 kHz之内.AE信号在频率峰值上有稍微的变化：砂轮轻度磨损时主要峰值频率29 kHz、95 kHz和201 kHz;砂轮严重磨损时主要峰值频率30 kHz、88 kHz和220 kHz.金刚石砂轮表面状态对磨削过程有重要的影响，砂轮磨损后磨粒的切削刃钝化，磨削力加大磨削温度升高.

经验模态分解EMD[1]方法是将非线性非平稳的砂轮磨损声发射信号自适应分解成一系列平稳的固有模态函数IMF，所分解出来的各IMF分量包含了原声发射信号的不同时间尺度的局部特征信号，并且无须预先设定任何基函数，优于传统的傅里叶变换和小波变换声发射信号分析方法.在磨削金刚石砂轮与陶瓷工件的声发射信号较低频率段中，一般是磨削液和机床运动部件摩擦产生的噪声;这样就可以把分布在较高频率段的金刚石砂轮磨粒与陶瓷工件的切削、滑擦和犁耕以及切屑断裂、磨粒破裂等产生的声发射信号[12-13]清晰地提取出来进行分析.

采集到的PSZ磨削实验声发射波形流信号转化为文本文件，并导入MATLAB软件中的EMD工具箱将采集到的声发射信号进行EMD分解，每个声发射信号可以分解为12～16个固有模态函数（IMF）和一个剩余信号.固有模态函数和剩余信号与原始信号的相关系数很大程度上可以反映它们之间的相关程度，相关系数越大说明IMF含原信号中的有效成分越高[1].PSZ磨削声发射信号经验模态分解信号的相关系数如图3所示，可以看出imf1～imf6与原始信号的相关系数较大，其中又以imf4、imf5、imf3的相关系数最大;imf7之后固有模态函数和剩余信号与原始信号的相关系数接近零即可以剔除.因此固有模态函数imf1～imf6包含了原始信号中主要的有效成分，可以作为原始信号的代表信号，从中可以提取信息用于砂轮磨损状态的监测.

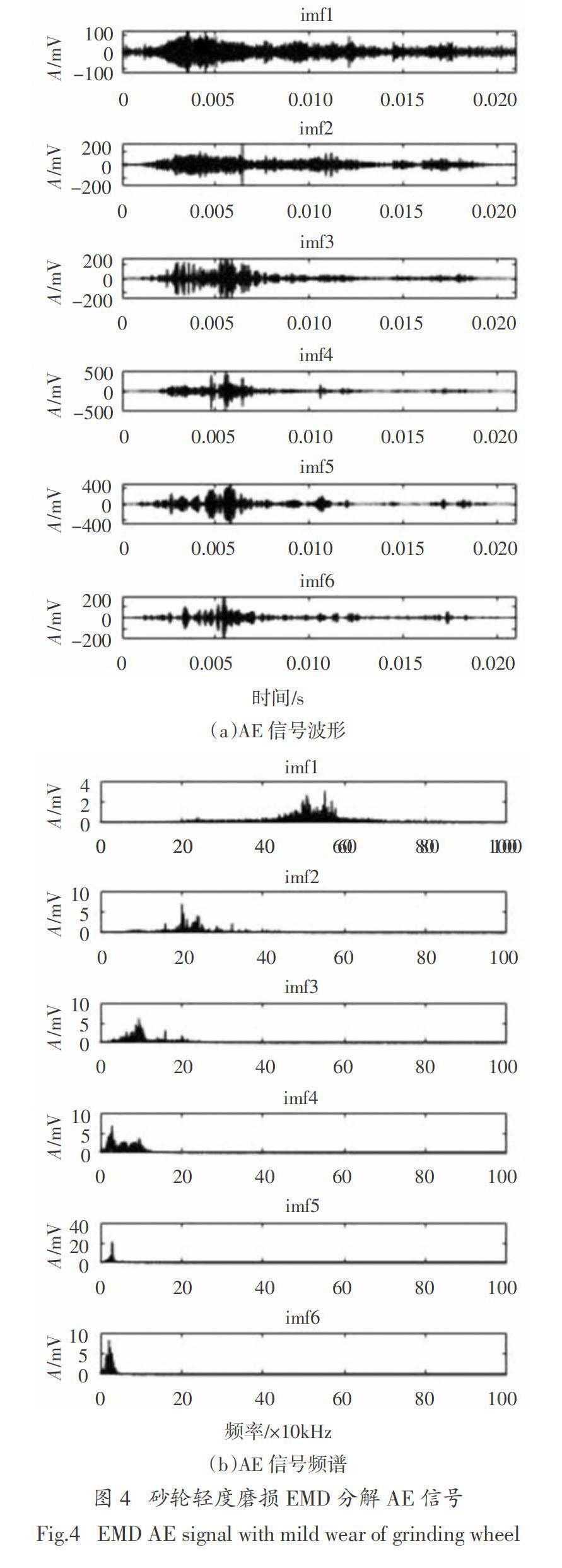
砂轮不同磨损状态时的声发射信号经过经验模态分解得到的imf1～imf6信号的波形和频谱，如图4和图5.从频谱图5可见，不同固有模态函数的频率范围有明显的区别：imf1信号的主要频率在550 kHz附近;imf2的主要频率在210 kHz附近;imf3的主要频率在100 kHz附近;imf4的主要频率在50

kHz附近;imf5 和imf6的主要频率在30 kHz附近.砂轮轻度磨损与严重磨损时的声发射信号经过EMD处理的各阶固有模态函数频率主要分布范围和主要的峰值频率上没有明显的变化;但是从表1中看出，砂轮严重磨损时的波形幅值明显大于砂轮轻度磨损时的波形幅值.随着砂轮磨损加剧，固有模态函数imf1～imf6的幅值增大，也就是各个分量的能量出现了不同程度的增大，其中高频分量imf1～imf3对应幅值增大明显在两倍以上;而低频分量imf4～imf6的增加较小.说明随着金刚石砂轮磨损程度的加深，AE信号高频成分在不断增加.砂轮在轻度磨损到严重磨损imf1～imf6的幅值都有明显增大，所以它们都是砂轮磨损的特征量.

原始磨削声发射信号三个峰值频率分别在30 kHz、100 kHz和210 kHz附近，这与经验模态分解得到的固有模态函数imf2～imf6的主要频率（如表1）相似，因而可以说imf2～imf6中分别包含了原始声发射信号中的一个重要频率段的主要信息，imf2包含原信号中220 kHz频率附近的大量信息，imf3包含原信号中100 kHz频率附近的大量信息，imf4～imf6包含原信号中30 kHz频率附近的大量信息，而imf1则包含了400 kHz以上的高频部分的主要信息，因而固有模态函数imf1～imf6与原始AE信号密切相关，所以它们的相关系数较大.

分析还可见固有模态函数imf1～imf6的能量占据了AE信号总能量的很大比重，imf1～imf6信号的总能量占据了原始AE信号总能量的全部（98%以上），其中imf3～imf5（频率主要在100 kHz以下）起主要作用，占据了原始AE信号总能量的85%以上，可以看出磨削氧化鋯PSZ陶瓷的声发射信号频率主要集中在100 kHz以内.同时由图3可见imf3～imf5的相关系数最大，所以相关系数与声发射信号能量密切相关.

3   砂轮磨损声发射信号特征提取

对EMD分解得到的固有模态函数imf1～imf6进行分析，利用式（1）～（3）计算每个IMF的有效值（IMFrms）、方差（IMFvar）、能量系数（IMFpe）.金刚石砂轮的磨损加剧，磨削AE信号增强则其有效值增大.随着金刚石砂轮的磨损，砂轮表面的金刚石磨粒钝化，切除PSZ材料的能力下降，与之对应的AE声发射信号也会出现更大的波动，即AE信号方差增大.AE信号能量系数，即每个固有模态函数的能量所占原始信号总能量的百分比，由于每个固有模态函数所对应的AE信号主要频率不同，能量系数也在一定程度代表了不同频率段所占据的能量比重.砂轮的磨损声发射信号频率有从低频向高频移动的趋势，这一特征可以用能量系数来表征.砂轮轻度磨损与砂轮严重磨损声发射信号特征值如图6～8所示.

固有模态函数有效值 的计算公式：

式（1）中： i表示数据点; N表示信号长度即信号总的数据点数;j表示第j个固有模态函数;xj（i）表示第j个固有模态函数的第i个数据点;IMFrms（j）表示第j个固有模态函数的有效值.

固有模态函数方差IMFvar的计算公式：

式（2）中：i表示数据点; N表示信号长度即信号总的数据点数;j表示第j个固有模态函数;xj（i）表示第 j个固有模态函数的第i个数据点;μj表示第 j个固有模态函数的平均值;IMFvar（j）表示第j个固有模态函数的方差.

固有模态函数能量系数 的计算公式：

式（3）中： i表示数据点; N表示信号长度即信号总的数据点数;j表示第j个固有模态函数; m表示经验模态分解得到的信号数目;xj（i）表示第j个固有模态函数的第i个数据点;μj表示第j个固有模态函数的平均值;IMFpe（j）表示第j个固有模态函数的能量系数.

从图6可以明显看出：砂轮磨损严重时，各固有模态函数imf1～imf6的有效值IMFrms要大于轻度砂轮磨损的有效值，所以有效值可以作为砂轮磨损状态判别的特征量.砂轮的磨损加剧使磨粒切削刃变钝，磨粒滑擦作用增强磨削能量增加，声发射信号的幅值增大，导致每个固有模态函数的IMFrms增加.但是由于磨削PSZ的AE信号主要频率在100 kHz以内，因而每个固有模态函数的IMFrms增大程度不同.其中imf3～imf5的有效值的增大最为明显， imf3～imf5的相关系数最大，其主要频率在100 kHz以下并且占据了总能量的85%以上，是磨削氧化锆陶瓷时声发射信号的主要频率范围.因而在砂轮磨损状态变化引起声发射源变化时，在imf3～imf5上的反应更为明显，而imf1、imf2和imf6的变化较小.

从图7可以明显看出：砂轮磨损严重时，各固有模态函数imf1～imf6的方差IMFvar要大于砂轮轻度磨损方差值，是砂轮磨损状态的特征量.金刚石砂轮的磨损使金刚石磨粒切削刃变钝，PSZ陶瓷材料切除变得困难，磨削变得不稳定，声发射信号出现更大的波动，因而固有模态函数方差IMFvar有变大趋势.但是因为磨削氧化锆的声发射信号的主要频率不同，在不同的固有模态函数方差IMFvar的增大程度不一样.由于imf3～imf5的主要频率在100 kHz以下并且占据了总能量的85%以上，集中了磨削PSZ陶瓷时声发射信号的大部分能量，imf3～imf5的方差值的变化最为明显，而imf1、imf2和imf6则增大相对较小.

固有模态函数的能量系数IMFpe表示了每个固有模态函数的能量所占AE原始信号总能量的百分比，能量系数越大，则表明该固有模态函数对AE原始信号的贡献越多.从图8可以看出：在不同砂轮磨损状态下固有模态函数imf1～imf6的能量系数各不相同，但是它们都主要集中在了imf3～imf5上，并且砂轮严重磨损与砂轮轻度磨损相比，imf3和imf4的能量系数增大，imf5的能量减小.这是因为imf3～imf5的相关系数大，其主要频率在100 kHz以下，是磨削氧化锆陶瓷时声发射信号的主要频率范围.当砂轮磨损严重时，主要频率有轻微地向高频部分移动的趋势，因而imf3和imf4能量比重增加，imf5（主要频率分布范围比imf3和imf4低）的能量比重减少.至于imf1、imf2频率较高，所占原信号的比重不大;而imf6的频率低.

4   基于LS-SVM的砂轮磨损状态监测

支持向量机（SVM， Support Vector Machine）克服了过拟合、泛化能力差等问题，在解决小样本、非线性、局部极小和高维模式识别问题中优势明显.但是标准支持向量机SVM训练样本时因为求解二次规划问题而训练速度慢，在磨削实时监测中对大量的声发射信号数据可能来不及处理，为此应用最小二乘支持向量机（LS-SVM， Least Squares Support Vector Machine）[1]来提高训练速度，为工程陶瓷磨削金刚石砂轮磨损状态的智能在线监测打下基础.

实验获得不同砂轮磨损状态的磨削声发射信号共40组，其中砂轮轻度磨损20组，砂轮严重磨损20组.经过EMD分解从固有模态函数imf1～imf6中分别提取有效值（IMFrms）、方差（IMFvar）、能量系数（IMFpe）.有效值（IMFrms），方差（IMFvar），能量系数（IMFpe）各为一组，分别作为LS-SVM的输入特征向量数据集，见表2～4.每组输入特征向量数据集的原始数据集被分为两部分：一部分共30组用于LS-SVM的训练，其中砂轮严重磨损和砂轮轻度磨损状态各15组;另一部分10组用于砂轮磨损状态的预测，其中砂轮严重磨损和砂轮轻度磨损状态各5组.每个输入特征向量由6个特征值组成，分别为固有模态函数imf1～imf6的有效值（IMFrms）或方差（IMFvar）或能量系数（IMFpe）.

为了减少AE信号数据大小差距过大对LS-SVM识别精度的影响，预先对磨削AE信号原始数据进行归一化处理，采用最小-最大标准化方法，将原始数据映射到[0 1]之间，即

式（4）中： X为原始数据;Xmax为原始数据中的最大值;Xmin为原始数据中的最小值; X*为归一化的数据.砂轮的磨损状态为两类，用“0”表示砂轮轻度磨损，用“1”表示砂轮严重磨损.由以上得到LS-SVM的样本集{（xi，yi）}，其中xi是由AE信号归一化后的LS-SVM输入特征组成的矩阵，代表第i个输入特征向量;yi∈{0，1}，为分类标签代表第i个输入特征向量对应的砂轮磨损状态.选用径向基核函数作为LS-SVM的核函数;正则化参数c和核函数参数σ是需要优化的两个重要参数，采用交叉验证的方法得到，解决了LS-SVM欠学习和过学习的问题.

从金刚石砂轮磨损状态预测结果（见表5）来看，输入特征分别为有效值（IMFrms）或方差（IMFvar）或能量系数（IMFpe）时，磨削金刚石砂轮磨损状态的LS-SVM预测正确率都达到了100%，很好地实现了金刚石砂轮磨损状态监测;同时也说明了所提取磨削声发射信号特征对砂轮磨损状态监测的合理性.

5   结   论

砂轮磨损加剧会导致磨粒摩擦作用增强而切削作用下降，反映在PSZ陶瓷磨削AE信号高频率分量增强明显，并且有从低频向高频转移的趋势.结合工程陶瓷部分稳定氧化锆PSZ磨削过程中AE信号非线性非平稳性的特点，采用经验模态分解EMD方法将其AE信号分解为多个平稳的固有模态函数之和.随着金刚石砂轮从轻度磨损转变为严重磨损，即砂轮磨损加剧时，其磨削声发射信号各固有模态函数的有效值和方差不同程度的增大，能量系数在imf3～imf5上亦表现出由低频向高频移动的特点.分别用磨削声发射信号的固有模态函数imf1～imf6的有效值（IMFrms）、方差（IMFvar）和能量系数（IMFpe）作为特征向量，用最小二乘支持向量机智能监测PSZ磨削中金刚石砂轮轻度磨损和严重磨损状态取得了很好的效果.

参考文献

[1]    聂鹏，董慧，李正强，等. 基于改进 EMD 和 LS-SVM 的刀具磨损状态识别[J]. 北京工业大学学报，2013，39（12）：1784-1790.

NIE P，DONG H，LI Z Q，et al. State recognition of tool wear based on improved empirical mode decomposition and least squares support vector machine[J]. Journal of Beijing University of Technology，2013，39（12）：1784-1790.（In Chinese）

[2]    NAKAI M E，AGUIAR P R，GUILLARDI H，et al. Evaluation of neural models applied to the estimation of tool wear in the grinding of advanced ceramics[J]. Expert Systems with Applications，2015，42：7026-7035.

[3]    聂鹏，徐洪圭，刘新宇，等. EEMD方法在刀具磨损状态识别的应用[J]. 传感器与微系统，2012，31（5）：147-149.

NIE P，XU H Y，LIU X Y，et al. Application of EEMD method in state recognition of tool wear[J]. Transducer and Microsystem Technologies，2012，31（5）：147-149.（In Chinese）

[4]    李慶，宋万清. IMF奇异值熵的刀具磨损状态诊断[J]. 制造业自动化，2013，35（12）：52-55.

LI Q，SONG W Q. Tool wear state diagnosis with IMF singular value entropy[J]. Manufacturing Automation，2013，35（12）：52-55.（In Chinese）

[5]    杨振生. 面向磨削烧伤问题的间接监测技术研究[D]. 杭州：浙江大学，2013.

YANG Z S.  Research on the indirect monitoring technique of grinding burn and its interrelated problems in precision grinding process[D]. Hangzhou： Zhejiang University，2013.（In Chinese）

[6]    孫惠斌，牛伟龙，王俊阳. 基于希尔伯特黄变换的刀具磨损特征提取[J]. 振动与冲击，2015，34（4）：158-164.

SUN H B，NIU W L，WANG J Y. Tool wear feature extraction based on Hilbert-Huang transformation[J]. Journal of Vibration and Shock，2015，34（4）：158-164.（In Chinese）

[7]    关山，彭昶. 刀具磨损声发射信号的混沌特性分析[J]. 农业工程学报，2015，31（11）：60-65

GUAN S，PENG C. Chaotic characteristic analysis of tool wear acoustic emission signal[J]. Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE），2015，31（11）： 60-65. （In Chinese）

[8]    CHEN X，？魻P？魻Z T T. Effect of different parameters on grinding efficiency and its monitoring by acoustic emission[J]. Production & Manufacturing Research，2016，4（1）：190-208.

[9]    彭延峰，刘贞涛，程军圣，等. 基于初值优化的自适应最稀疏时频分析方法[J]. 湖南大学学报（自然科学版），2017， 44（8）：50-56.

PENG Y F，LIU Z T，CHENG J S，et al. Adaptive and sparsest time-frequency analysis method based on initial value optimization [J]. Journal of Hunan University（Natural Sciences），2017，44（8）：50-56.（In Chinese）

[10]  LIAO T W. Warren Liao. Feature extraction and selection from acoustic emission signals with an application in grinding wheel condition monitoring[J]. Engineering Applications of Artificial Intelligence， 2010，23：74-84.

[11]  石建，丁宁. 基于声发射技术的砂轮磨损状况在线检测[J]. 长春大学学报，2013，23（8）：931-936.

SHI J，DING N. On-line detection of the state of grinding wheel wear based on acoustic emission technique[J]. Journal of Changchun University，2013，23（8）：931-936.（In Chinese）

[12]  MOHAMMED A，FOLKES J，CHEN X.  Detection of grinding temperatures using laser irradiation and acoustic emission sensing technique[J]. Materials and Manufacturing Processes，2012，27（4）：395-400.

[13]  CHEN X，GRIFFIN J，LIU Q.  Mechanical and thermal behaviors of grinding acoustic emission[J]. International Journal of Manufacturing Technology and Management，2007，12（1/2/3）：184-199.